МОДЕЛИРОВАНИЕ ПОВЕРХНОСТЕЙ
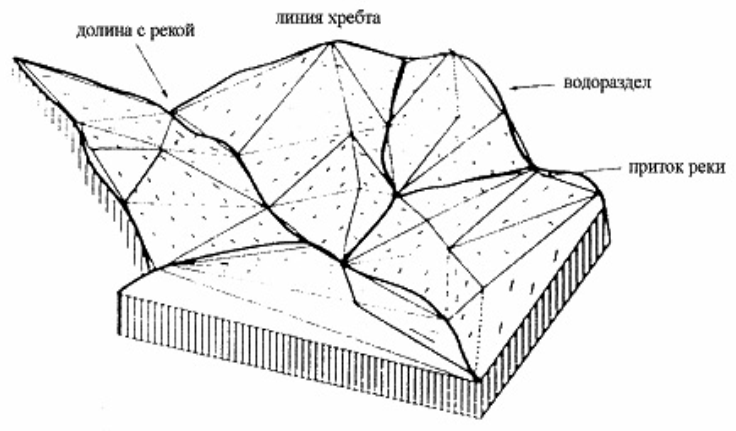
Поверхность и цифровая модель
Основой для представления данных о земной поверхности являются цифровые модели рельефа.
Поверхности – это объекты, которые чаще всего представляются значениями высоты Z, распределенными по области, определенной координатами X и Y.
Цифровые модели рельефа (ЦМР) используют для компьютерного представления земных поверхностей.
| ЦМР – средство цифрового представления рельефа земной поверхности. |
Построение ЦМР требует определённой формы представления исходных данных (набора координат точек X,Y,Z) и способа их структурного описания, позволяющего восстанавливать поверхность путем интерполяции или аппроксимации исходных данных.
Источники данных для формирования ЦМР
Исходные данные для формирования ЦМР могут быть получены по картам – цифрованием горизонталей, по стереопарам снимков, а также в результате геодезических измерений или лазерного сканирования местности. Наиболее распространен первый способ, т.к. сбор по стереопарам снимков отличается трудоемкостью и требует специфического программного обеспечения, но в то же время позволяет обеспечить желаемую степень детальности представления земной поверхности. Лазерное сканирование перспективный современный метод, пока достаточно дорогой.
Построение ЦМР требует определенной структуры данных, а исходные точки могут быть по разному распределены в пространстве. Сбор данных может осуществляться по точкам регулярной сетки, по структурным линиям рельефа или хаотично. Первичные данные с помощью тех или иных операций приводят к одному из наиболее распространенных в ГИС структур для представления поверхностей: GRID, TIN или TGRID.
TIN (Triangulated Irregular Network) – нерегулярная триангуляционная сеть, система неперекрывающихся треугольников. Вершинами треугольников являются исходные опорные точки. Рельеф в этом случае представляется многогранной поверхностью, каждая грань которой описывается либо линейной функцией (полиэдральная модель), либо полиноминальной поверхностью, коэффициенты которой определяются по значениям в вершинах граней треугольников. Для получения модели поверхности нужно соединить пары точек ребрами определенным способом, называемым триангуляцией Делоне (рис. 5).
Рис. 5. TIN модель
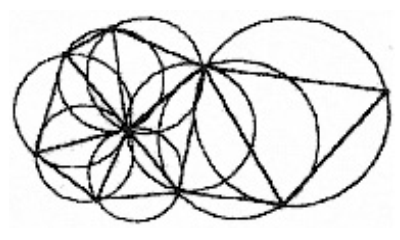
Триангуляция Делоне в приложении к двумерному пространству формулируется следующим образом: система взаимосвязанных неперекрывающихся треугольников имеет наименьший периметр, если ни одна из вершин не попадает внутрь ни одной из окружностей, описанных вокруг образованных треугольников (рис.6).
Образовавшиеся треугольники при такой триангуляции максимально приближаются к равносторонним, а каждая из сторон образовавшихся треугольников из противолежащей вершины видна под максимальным углом из всех возможных точек соответствующей полуплоскости. Интерполяция выполняется по образованным ребрам.
Рис. 6. Триангуляция Делоне
Отличительной особенностью и преимуществом триангуляционной модели является то, что в ней нет преобразований исходных данных. С одной стороны, это не дает использовать такие модели для детального анализа, но с другой стороны, исследователь всегда знает, что в этой модели нет привнесенных ошибок, которыми грешат модели, полученные при использовании других методов интерполяции. Немаловажен и тот факт, что это самый быстрый метод интерполяции. Однако, если в ранних версиях большинства ГИС триангуляционный методы был основной, то сегодня большое распространение получили модели в виде регулярной матрицы значений высот.
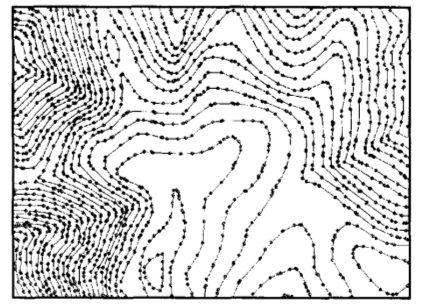
GRID – модель, представляет собой регулярную матрицу значений высот, полученную при интерполяции исходных данных. Для каждой ячейки матрицы высота вычисляется на основе интерполяции. Фактически это сетка, размеры которой задаются в соответствии с требованиями точности конкретной решаемой задачи. Регулярная сетка соответствует земной поверхности, а не изображению.
При использовании GRID-модели существует некоторая сложность в выборе интервала между точками. Например, участки поверхности могут быть как сильно пересеченными, так и выположенными. В первом случае необходимо большее количество точек на единицу площади.
Рис. 7. Плотность точек в модели GRID
TGRID (triangulated grid) – модель, сочетающая в себе элементы моделей TIN и GRID. Такие модели имеют свои преимущества, например, позволяют использовать дополнительные данные для описания сложных форм рельефа (обрывы, скальные выступы).
Восстановление поверхностей реализуется на основе интерполяции исходных данных.
Интерполяция – восстановление функции на заданном интервале по известным ее значениям конечного множества точек, принадлежащих этому интервалу.
В настоящее время известны десятки методов интерполяции поверхностей, наиболее распространенные: линейная интерполяция; метод обратных взвешенных расстояний, кригинг; сплайн-интерполяция; тренд-интерполяция.
Кригинг. Метод интерполяции, который основан на использовании методов математической статистики. В его реализации применяется идея регионализированной переменной, т.е. переменной, которая изменяется от места к месту с некоторой видимой непрерывностью, поэтому не может моделироваться только одним математическим уравнением. Поверхность рассматривается в виде трех независимых величин. Первая — тренд, характеризует изменение поверхности в определенном направлении. Далее предполагается, что имеются небольшие отклонения от общей тенденции, вроде маленьких пиков и впадин, которые являются случайными, но все же связанными друг с другом пространственно.
Наконец, имеется случайный шум (например, валуны). С каждой из трех переменных надо оперировать в отдельности. Тренд оценивается с использованием математического уравнения, которое наиболее близко представляет общее изменение поверхности, во многом подобно поверхности тренда.
Рис. 8. Элементы кригинга: 1 — тренд, 2 — случайные, но пространственно связанные высотные колебания, 3 — случайный шум.
Ожидаемое изменение высоты измеряется по вариограмме, на которой по горизонтальной оси откладывается расстояние между отсчетами, а на вертикальной — полудисперсия. Полудисперсия определяется как половина дисперсии между значениями высоты исходных точек и высот соседних точек. Затем через точки данных проводится кривая наилучшего приближения. Дисперсия в какой-то момент достигает максимума и остается постоянной (выявляется предельный радиус корреляции).
Интерполяция методом кригинга в большинстве случаев дает хорошие результаты, даже когда плотность исходных точек не велика. Однако, при некотором расположении точек возможно появление резких пиков и впадин.
Метод обратных взвешенных расстояний. Этот метод основан на предположении, что чем ближе друг к другу находятся исходные точки, тем ближе их значения. Для точного описания топографии набор точек, по которым будет осуществляться интерполяция, необходимо выбирать в некоторой окрестности определяемой точки, так как они оказывают наибольшее влияние на ее высоту. Это достигается следующим образом. Вводится максимальный радиус поиска или количество точек, ближайших по расстоянию от начальной (определяемой) точки. Затем значению высоты в каждой выбранной точке задается вес, вычисляемый в зависимости от квадрата расстояния до определяемой точки. Этим достигается, чтобы более близкие точки вносили больший вклад в определение интерполируемой высоты по сравнению с более удаленными точками.
Тренд интерполяция. В некоторых случаях исследователя интересуют общие тенденции поверхности, которые характеризуются поверхностью тренда.
Аналогично методу обратных взвешенных расстояний для поверхности тренда используется набор точек в пределах заданной окрестности. В пределах каждой окрестности строится поверхность наилучшего приближения на основе математических уравнений, таких как полиномы или сплайны.
Поверхности тренда могут быть плоскими, показывая общую тенденцию или более сложными. Тип используемого уравнения или степень полинома определяет величину волнистости поверхности. Например, поверхность тренда первого порядка будет выглядеть как плоскость, пересекающая под некоторым углом всю поверхность. Если поверхность имеет один изгиб, то такую поверхность называют поверхностью тренда второго порядка.
Сплайн интерполяция. Возможность описания сложных поверхностей с помощью полиномов невысоких степеней определяется тем, что при сплайн интерполяции вся территория разбивается на небольшие непересекающиеся участки. Аппроксимация полиномами осуществляется раздельно для каждого участка. Обычно используют полином третьей степени — кубический сплайн. Затем строится общая функция «склейки» на всю область, с заданием условия непрерывности на границах участков и непрерывности первых и вторых частных производных, т.е. обеспечивается гладкость склеивания полиномов.
Сглаживание сплайн-функциями особенно удобно при моделировании поверхностей, осложненных разрывными нарушениями, и позволяет избежать искажения типа «краевых эффектов».
Дата добавления: 2015-11-24 ; просмотров: 888 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
GRID-модели представления поверхностей. Их премущество и не достатки
GRID — модель, представляет собой регулярную матрицу значений высот, полученную при интерполяции исходных данных. Для каждой ячейки матрицы высота вычисляется на основе интерполяции. Фактически это сетка, размеры которой задаются в соответствии с требованиями точности конкретной решаемой задачи. Регулярная сетка соответствует земной поверхности, а не изображению.GRIDы представляют поверхности по регулярно распределенным точкам. TINы представляют поверхности на основе нерегулярного пространственного распределения точек.Преимущества и недостатки GRID.Модель грид достаточно простая, ее обработка
обычно более эффективна, чем других моделей. Хорошо разработанные алгоритмы обработки гридов в массе своей проистекают из методов обработки растровых изображений. Данных по высотам рельефа в формате грида достаточно много и они относительно дешевы. С другой стороны, регулярная структура данных не в полной мере подходит для описания изменчивой поверхности (потеря информации в промежутках между точками регулярной сетки, или ее избыточность в случае плавно изменяющихся поверхностей). Кроме того, базовая структура грида не позволяет адекватно показать линейные объекты в приложениях, где требуются крупные масштабы.
Выбор проектировании при создания проекта ГИС
При проектировании информационной системы нужно иметь в виду, что информационные потребности управляющих различны в зависимости от их уровня в иерархии и функциональных обязанностей.
Принято разделять виды управленческой деятельности на три категории.
1. Стратегическое планирование — процесс принятия решений относительно целей и стратегий организации. Изменение целей, использование ресурсов для достижения этих целей. Выбор стратегий, обусловливающих получение, использование и размещение этих ресурсов.
2.Управленческий контроль — процесс, посредством которого управляющие обеспечивают получение ресурсов и их эффективное использование для достижения общих целей.
3.Оперативный контроль — процесс обеспечения эффективного и квалифицированного выполнения конкретных задач.
Системы, создаваемые для разных категорий управления, различны.
Дата добавления: 2018-08-06 ; просмотров: 1929 ; Мы поможем в написании вашей работы!
Источник
Анализ сущности GRID-модели, выявление преимуществ и недостатков данной модели в процессе построения цифровых моделей рельефа , страница 3
– на основе ресурсов ГИС осуществить оптимизацию задач (поставка в кратчайшие сроки с минимальными затратами).
Таким образом, эффективность решения стоящих перед бизнесменами задач с помощью ГИС значительно повышается, так как ГИС позволяет создавать картографические изображения и карты для презентаций, отображать и анализировать бизнес-информацию новыми методами, выявлять скрытые ранее взаимосвязки. За счет этого появляется преимущество в конкурентной борьбе, так как быстрее находится оптимальное решение, выявляются новые рынки сбыта своих товаров и услуг, лучше обслуживаются заказчики, контролируются и оптимально перераспределяются материальные и финансовые ресурсы.[2]
ГЛАВА 2. ПОНЯТИЕ О GRID-МОДЕЛИ
Растровая модель рельефа предусматривает разбиение пространства на далее не делимые элементы (пикселы), образуя матрицу высот – регулярную сеть высотных отметок. Подобные цифровые модели рельефа создаются национальными картографическими службами многих стран.
Для представления двумерных моделей поверхностей в геоинформационных системах используют гриды, что в перевод на русский язык означает «сетки». Сетка данная является прямоугольной и представляет собою матрицу из вещественных чисел. Такого рода модель поверхности очень проста и удобна. Любой человек, посмотрев на нее, может сразу понять, как она устроена.[3]
Рис. 1. Общее представление GRID-модели
Регулярная сеть высот представляет собой решетку с равными прямоугольниками или квадратами, где вершины этих фигур являются узлами сетки (рис. 1).
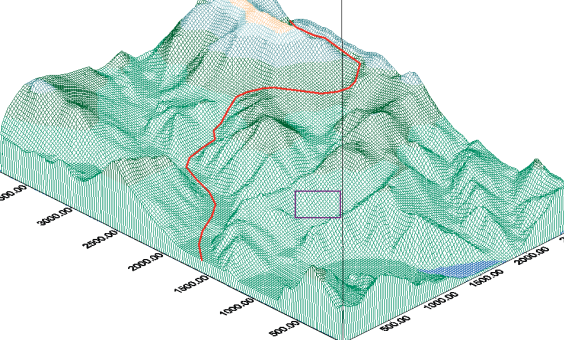
Рис. 2. Трёхмерная модель рельефа окрестностей пос. Коммунар (Хакасия), которая построена на основе регулярной сети высот
Одним из первых пакетов программ, в котором была осуществлена реализация возможности множественного ввода разных слоёв растровых ячеек, был пакет GRID (перевод с англ. – решетка, сетка, сеть), который был создан в конце 1960-х гг. в Гарвардской лаборатории машинной графики и пространственного анализа (США). В современном широко распространённом ГИС-пакете ArcGIS (раньше – ARC/INFO (ESRI Inc.)) растровую модель пространственных данных также именуют GRID.
В другой популярной программе для расчёта ЦМР – Surfer (Golden Software Inc.) регулярная сеть высот также называется GRID, файлы такого рода ЦМР имеют формат GRD, а расчёт подобного рода модели именуют Gridding. Очевидно, поэтому относительно регулярной сети высот в нашем государстве получили распространение термины «грид» и «гридинг», которые ряд ученых и практиков рассматривают в качестве примеров научного жаргона.
В процессе создания регулярной сети высот (GRID) очень важным является учет плотности сетки (шаг сетки), определяющий её пространственное разрешение (см. рис. 3, 4). Чем меньше выбранный шаг, тем более точной является ЦМР – выше пространственное разрешение модели, но тем большим является количество узлов сетки, значит, требуется значительное времени для расчета ЦМР и больше места на диске. К примеру, при уменьшении шага сетки в 2 раза, происходит возрастание в 4 раза объёма компьютерной памяти, которая необходима для хранения модели. Отсюда следует, что необходимо нахождение баланса. К примеру, стандарт на ЦМР Геологической съемки США, который был разработан для Национального цифрового картографического банка данных, специфицирует цифровую модель рельефа как регулярный массив высотных отметок в узлах решетки 30х30 м для карты масштаба 1:24 000.[4]
Рис. 3. Увеличенный фрагмент модели рельефа на рис. 2, который показывает растровую структуру модели
Источник