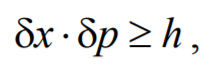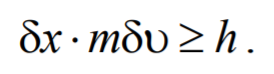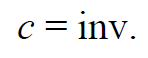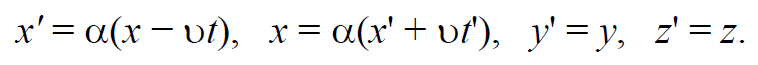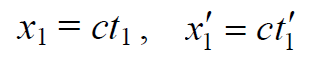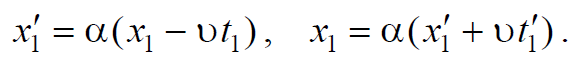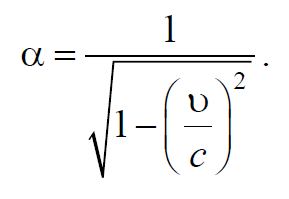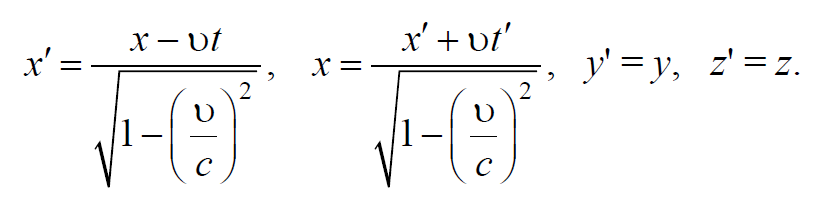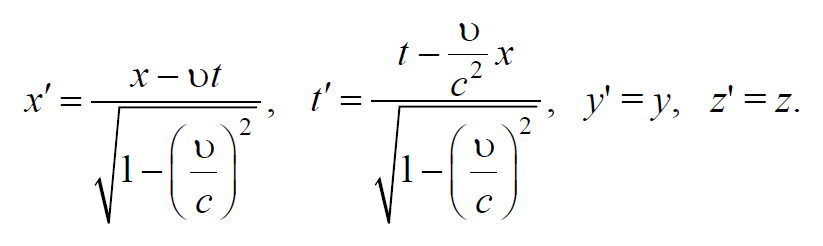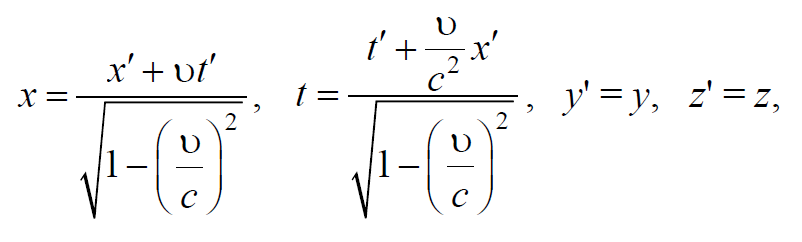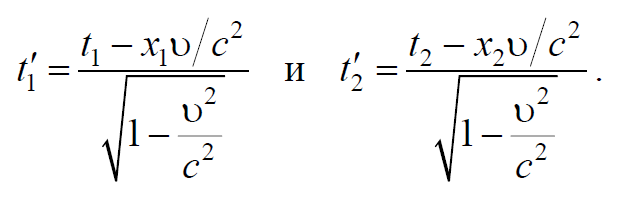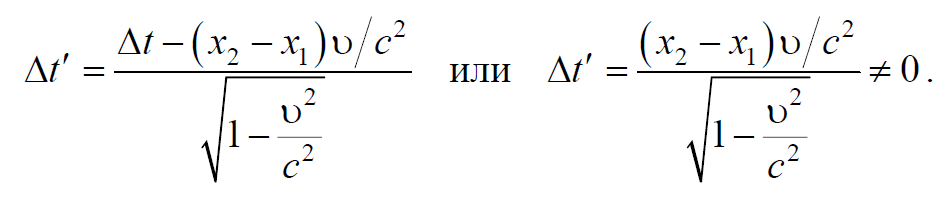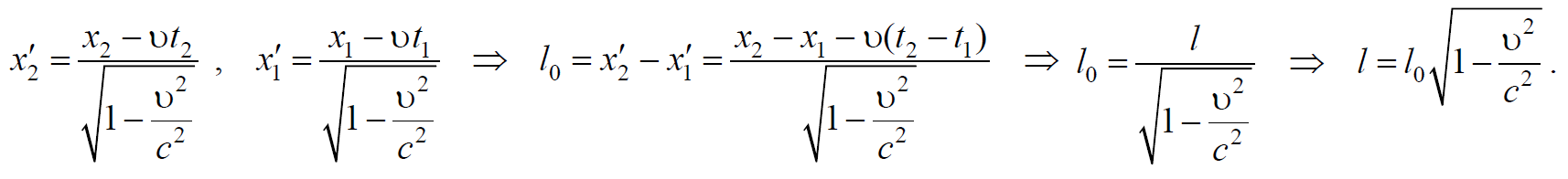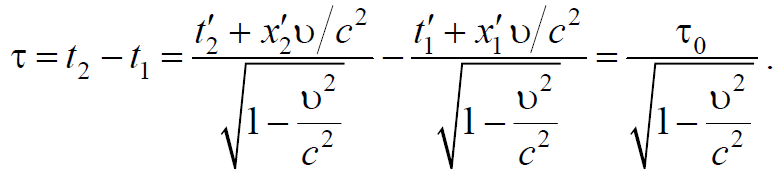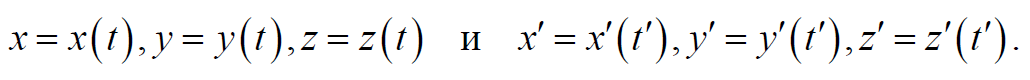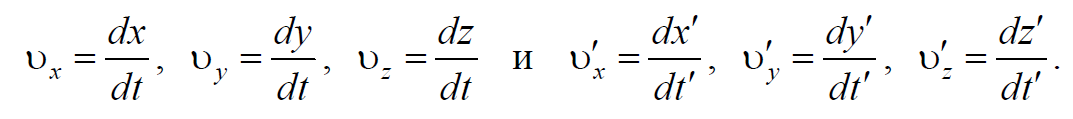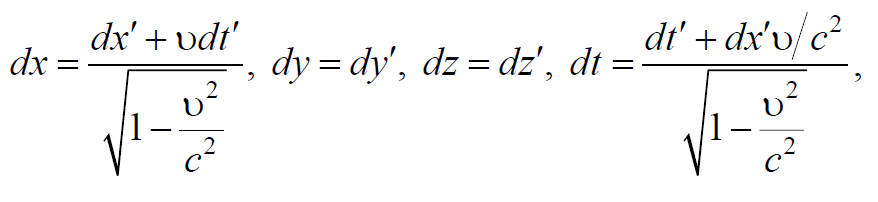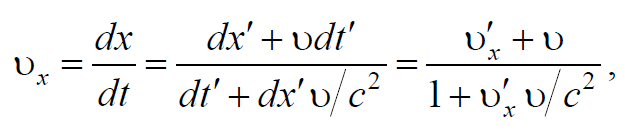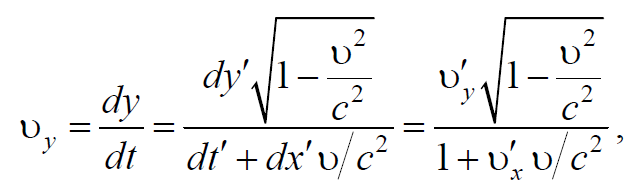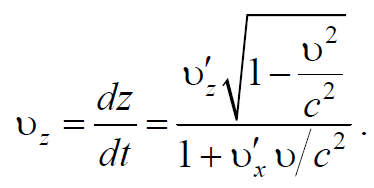Границы применимости классического способа описания движения точки

Границы применимости классического способа описания движений.

В классической механике состояние движения частицы в любой момент времени характеризуется положением (координатой x при одномерном движении) и скоростью v. Вместо скорости можно пользоваться также импульсом, т.е. величиной p=mv, равной произведению массы частицы m на ее скорость. Образом частицы является геометрическая точка, описывающая с течением времени непрерывную траекторию. В квантовой механике показано, что такой способ описания движения имеет принципиальные границы применимости. Здесь преждевременно вдаваться в подробное обсуждение этого вопроса. Достаточно ограничиться предварительным сообщением основного результата, не касаясь его обоснования.

Согласно квантовой механике состояние частицы в каждый момент времени нельзя характеризовать точными значениями ее координаты и импульса в этот момент времени. Если в каком-либо состоянии координата известна с неопределенностью δx, а импульс — с неопределенностью δp, то обе эти величины одновременно не могут быть сделаны сколь угодно малыми. Они связаны соотношением

где h — универсальная постоянная, называемая постоянной Планка (1858—1947). Она играет основную роль во всех квантовых явлениях. Ее численное значение равно

Соотношение (1.5.1) называется принципом неопределенностей Гайзенберга. Оно определяет принципиальный предел точности одновременного измерения координаты и импульса частицы, который не может быть превзойден никаким усовершенствованием приборов и методов измерения. Дело здесь не в ошибках измерений. Такова уж природа реальных частиц, что мгновенные состояния их движения не могут быть охарактеризованы классически — точными значениями координат и импульсов. Частицы ведут себя более сложно, чем материальные точки классической механики. Классическая картина движения по непрерывным траекториям лишь приближенно соответствует законам природы. Границы ее применимости определяются соотношением неопределенностей (1.5.1). Из него следует, что мгновенное состояние движения частицы нельзя также характеризовать абсолютно точными значениями координаты и скорости. Неопределенности этих величин должны удовлетворять условию

Для макроскопических тел практическая применимость классического способа описания движения не вызывает сомнений. Допустим, например, что речь идет о движении шарика с массой m=1 г. Обычно положение шарика практически может быть определено с точностью до десятой или сотой доли миллиметра. Во всяком случае вряд ли имеет смысл говорить об ошибке в определении положения шарика, меньшей размеров атома. Положим поэтому δx=10−8 см. Тогда из соотношения неопределенностей (1.5.1) найдем

Одновременная малость величин δx и δv и является доказательством практической применимости классического способа описания движения для макроскопических тел. Не так обстоит дело, когда речь идет об атомных явлениях — явлениях, происходящих с частицами очень малой массы в очень малых объемах пространства. Рассмотрим, например, движение электрона в атоме водорода. Масса электрона m=9,11⋅10−28 г. Ошибка в положении электрона δx во всяком случае не должна превышать размеры атома, т.е. должно быть δx hmδx=6,63⋅10−279,11⋅10−28⋅10−8≈7⋅108 см/с.

Эта величина не меньше, а даже больше самой скорости электрона в атоме, которая по порядку величины равна 108 см/с. При таком положении классическая картина движения теряет всякий смысл.

10. Инерциальные системы отсчета –это система отсчета, в которой справедлив закон инерции: материальная точка, когда на нее не действуют никакие силы (или действуют силы взаимно уравновешенные), находится в состоянии покоя или равномерного прямолинейного движения.

Всякая система отсчета, движущаяся по отношению к инерциальной системе отсчета поступательно, равномерно и прямолинейно, есть также инерциальная система отсчета.

Следовательно теоретически может существовать любое число равноправных инерциальных систем отсчета, обладающих тем важным свойством, что во всех таких системах законы физики одинаковы (принцип относительности).

При переходе от одной инерциальной системы отсчета к другой в классической механике Ньютона для пространственных координат и времени справедливы преобразования Галилея (принцип относительности), а в релятивистской механике- преобразования Лоренца.

Считается, что система отсчета, движущаяся по отношению к инерциальной системе отсчета с ускорением, не инерциальна и закон инерции в ней не соблюдается.

Неинерциальная система отсчёта — система отсчёта, к которой не применим закон инерции (говорящий о том, что каждое тело, в отсутствие действующих на него сил, движется по прямой и с постоянной скоростью), и поэтому для согласования сил и ускорений в которой приходится вводить фиктивные силы инерции. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, является неинерциальной.

Законы Ньютона выполняются только в инерциальных системах отсчёта. Для того, чтобы найти уравнение движения в неинерциальной системе отсчёта, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной.

Классическая механика постулирует следующие два принципа:

1. время абсолютно, то есть промежутки времени между любыми двумя событиями одинаковы во всех произвольно движущихся системах отсчёта;

2. пространство абсолютно, то есть расстояние между двумя любыми материальными точками одинаково во всех произвольно движущихся системах отсчёта.

Эти два принципа позволяют записывать уравнение движения материальной точки относительно любой неинерциальной системы отсчёта, в которой не выполняется первый закон Ньютона.

Основное уравнение динамики относительного движения материальной точки имеет вид:

,

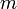
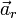
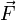
где — масса тела, — ускорение тела относительно неинерциальной системы отсчёта, — сумма всех внешних сил, действующих на тело, — переносное ускорение тела, — кориолисово ускорение тела.

Это уравнение может быть записано в привычной форме Второго закона Ньютона, если ввести фиктивные силы инерции:

· — переносная сила инерции

· — сила Кориолиса

Векторная величина, равная произведению массы материальной точки на её ускорение и направленная противоположно ускорению, называется силой инерции

Об ычные или простые силы инерции. К ним относится два слагаемых: — одно связано с неравномерным поступательным движением, а второе – с неравномерным вращением.

Центробежная сила — составляющая фиктивных сил инерции, которую вводят при переходе из инерциальной системы отсчёта в соответствующим образом вращающуюсянеинерциальную. Это позволяет в полученной неинерциальной системе отсчёта продолжать применять законы Ньютона для расчёта ускорения тел через баланс сил

Сила Кориолиса — одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения.

Источник

Лекция №11. Элементы релятивистской механики

7.1. Границы применимости классической механики

Классическая механика (иначе механика Ньютона) предопределило развитие физической науки, так как в ней были сформулированы количественные закономерности механического движения. В классической механике устанавливается способ описания движения материальных точек, что дает возможность теоретического объяснения механических явлений, встречающихся в природе.

Механика Ньютона покоится на прочном фундаменте экспериментальных фактов, однако все они относятся к медленным движениям макроскопических тел. Под медленными или нерелятивистскими движениями понимают движения, скорости которых очень малы по сравнению со скоростью света в вакууме с = 300 000 км/с . Движения, скорости которых приближаются к скорости света в вакууме, называют быстрыми или релятивистскими . В этом смысле движение спутника или космического корабля со скоростью υ = 8 км/с является еще очень медленным.

Теория относительности Эйнштейна предсказала, а опыт подтвердил это предсказание, что механика Ньютона не может быть применима к движениям частиц, скорости которых близки к скорости света в вакууме. На основе теории относительности была создана новая механика, применимая не только к медленным, но и к сколь угодно быстрым движениям. Она называется релятивистской механикой .

Согласно механике Ньютона скорость, до которой можно ускорить тело из состояния покоя, в принципе ничем не ограничена. По релятивистской механике значение скорости ускоряемого тела не может перейти через определенный предел, равный скорости света в вакууме с . В этом смысле скорость света с является предельной . Скорость тела не может ее достигнуть, но в принципе может подойти к ней сколь угодно близко.

Теория относительности установила границы применимости ньютоновской механики со стороны больших скоростей . Другое ограничение, и притом не только ньютоновской, но и релятивистской макроскопической механики, было получено в результате изучения микромира − мира атомов, молекул, электронов.

При изучении микромира физики сначала применяли понятия и законы, введенные и установленные для макроскопических тел. Электрон, например, рассматривался как твердый или деформируемый шарик, по объему которого как-то распределен электрический заряд. Считалось, что поведение электрона управляется теми же законами механики и электродинамики, которые были экспериментально установлены для макроскопических электрически заряженных тел. Считалось, что все понятия и законы макроскопической физики применимы и имеют смысл для тел сколь угодно малых размеров и для сколь угодно малых промежутков времени. Считалось, что для понимания явлений микромира не требуется новых понятий и законов, помимо тех, которыми располагает макроскопическая физика. Короче, микромир рассматривался просто как уменьшенная копия макромира. Такой подход к изучению явлений природы и теории, основанные на нем, называются классическими .

Опыты показали, что классический подход к изучению явлений микромира не применим, или точнее, его применимость к этому кругу явлений ограничена. Адекватное описание явлений микромира (применимое, конечно, также в каких-то пределах) дает квантовая механика , существенно отличающаяся от механики классической. Движение в микромире является более сложной формой движения, чем механическое перемещение тел в пространстве.

Таким образом, механика Ньютона имеет очень широкую и практически важную область применимости. В пределах этой области она никогда не утратит своего научного и практического значения. Отказываться от механики Ньютона надо лишь вне области ее применимости, когда она приводит либо к неверным, либо к недостаточно точным результатам. Такова, например, задача о движении заряженных частиц в ускорителях, где надо пользоваться релятивистской механикой. Таковы задачи о движении электронов в атомах, которые надо решать с помощью квантовой механики.

В классической механике состояние движения частицы в любой момент времени характеризуется положением (координатой х при одномерном движении) и скоростью υ . Вместо скорости можно пользоваться также импульсом , т. е. величиной p =m υ , равной произ ведению массы частицы m на ее скорость). Образом частицы является геометрическая точка, описывающая с течением времени непрерывную траекторию. В квантовой механике показано, что такой способ описания движения имеет принципиальные границы применимости.

Согласно квантовой механике состояние частицы в каждый момент времени нельзя характеризовать точными значениями ее координаты и импульса в этот момент времени. Если в каком-либо состоянии координата известна с неопределенностью δх , а импульс − с неопределенностью δр , то обе эти величины одновременно не могут быть сделаны сколь угодно малыми. Они связаны соотношением

где h − универсальная постоянная, называемая постоянной Планка в честь немецкого физика-теоретика Макса Планка (1858−1947).

Соотношение (7.1.1) называется принципом неопределенностей Гайзенберга по имени немецкого физика-теоретика Вернера Гайзенберга (1901−1976). Это соотношение определяет принципиальный предел точности одновременного измерения координаты и импульса частицы, который не может быть превзойден никаким усовершенствованием приборов и методов измерения. Дело здесь не в ошибках измерений. Такова природа реальных частиц, что мгновенные состояния их движения не могут быть охарактеризованы классически − точными значениями координат и импульсов. Частицы ведут себя более сложно, чем материальные точки классической механики. Классическая картина движения по непрерывным траекториям лишь приближенно соответствует законам природы. Границы ее применимости определяются соотношением неопределенностей (7.1.1). Из него следует, что мгновенное состояние движения частицы нельзя также характеризовать абсолютно точными значениями координаты и скорости. Неопределенности этих величин должны удовлетворять условию

Таким образом, применимость классической механики имеет следующие границы:

1) классическая механика применима для описания механических систем, в которых скорость составляющих ее объектов намного меньше скорости света (υ ;

2) классическая механика применима для описания только тех объектов, для которых динамические величины с размерностью действия намного больше постоянной Планка.

7.2. Постулаты Эйнштейна

В основе специальной теории относительности А. Эйнштейна лежат два постулата , смысл которых можно выразить так:

1. При одинаковых условиях, реализованных по отдельности в двух системах отсчета некоторой инерциальной системы К (I) и системы К’ (II) , движущейся равномерно и прямолинейно относительно системы I любые физические процессы в этих системах отсчета протекают одинаково, а описывающие их математические соотношения не изменяют своего вида при переходе из одной системы в другую. Этот постулат является обобщением механического принципа относительности Галилея на все без исключения физические явления.

2. В природе существует предельная (максимальная) скорость распространения физических сигналов (взаимодействий), одна и та же во всех инерциальных системах отсчета. Эта максимальная скорость совпадает со скоростью света в вакууме, она не зависит от движения источника и приемника света и равна с = 300 000 км/с.

Из первого принципа следует: если для данной задачи (некоторого класса задач) найдена инерциальная система отсчета I , то для этой задачи существует и бесчисленное множество инерциальных систем типа II , движущихся равномерно прямолинейно относительно I . Скорости всех систем II меньше с . Системы отсчета необходимо связывать с телами, а скорости тел не могут равняться или превосходить максимальную скорость света в вакууме, равную с . Скорости тел строго меньше максимальной.

Развитие науки показало, что оба принципа Эйнштейна подтверждаются всей совокупностью экспериментальных и теоретических знаний современной физики.

7.3. Преобразования Лоренца

Любой физический процесс − это последовательность событий. Событие определяется местом (координатами), где оно произошло, и моментом времени, когда оно произошло.

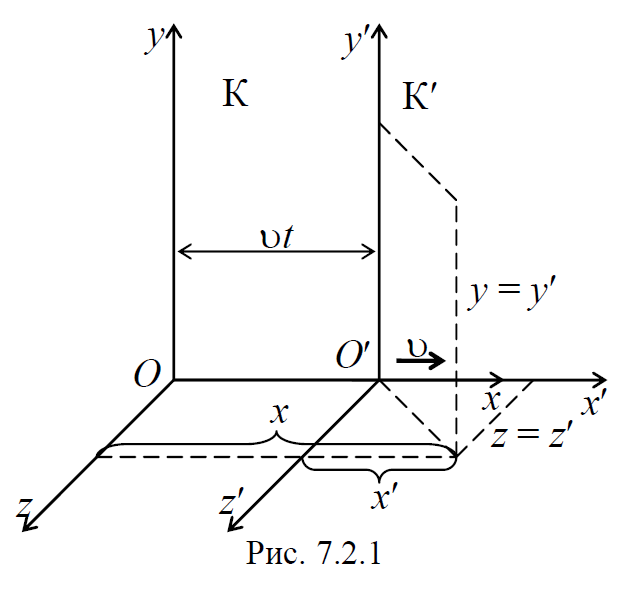
Пусть координаты некоторого события в системе отсчета I равны х , у , z , а в системе II они х’ , у’ , z’ (рис. 7.2.1). Установим связь между ними, исходя из принципов Эйнштейна, которая должна быть линейной, т. к. закон инерции подтверждается при всех скоростях, вплоть до максимальной скорости с (движение по прямой линии в системе I остается таковым и в системе II ). Поэтому форма связи должна быть следующей:

Множитель α в обеих формулах один и тот же, т. к. системы I и II совершенно равноправны. Формулы (7.3.1) относятся к любым событиям, а множитель α можно определить, рассматривая какое-либо частное событие. Для определения α , рассмотрим распространение света в направлении оси абсцисс от начала координат приход света в точку х₁ в момент t₁ (в системе I ), что также означает приход его в точку $$x^,_1$$ в момент $$t^,_1$$ (в системе II ).

В соответствии со вторым принципом Эйнштейна, путь света в системе I и II равен

и два равенства должны выполняться на основе формул (7.3.1)

Если два равенства (7.3.3) перемножить $$x_1x^,_1$$ и заменить на основании (7.3.2) через $$c^2t_1t^,_1$$ , то, после сокращения на $$t_1t^,_1$$ , получим $$c^2=α^2(c^2-υ^2)$$ , откуда

Подставляя найденное значение α в формулы (7.3.1), получим

Из второй формулы (7.3.5) легко определить t’ (после подстановки x’ ). Тогда окончательно имеем

Такова связь между координатами (включая время) одного и того же события в двух инерциальных системах отсчета I и II (штрихованная система I движется относительной не штрихованной II со скоростью υ в направлении оси х ).

Не составляет труда преобразовать формулы (7.3.6) к виду

что означает, что относительно системы K′ система K движется в отрицательном направлении оси x′ с той же самой скоростью υ .

Формулы (7.3.6) известны в науке как прямые преобразования Лоренца , а формулы (7.3.7) обратные преобразования Лоренца . Вся физическая теория (механика, электродинамика и др.) подлежала после их открытия такой перестройке, чтобы связи (7.3.6) и (7.3.7) были учтены. Это было осуществлено в специальной теории относительности (сначала в электродинамике Эйнштейном; позже – в механике).

7.4. Следствия из преобразований Лоренца

1) Относительность одновременности . Одновременность пространственно разделенных событий относительна. По определению, два события, которые происходят в разных точках $$х_1$$ и $$x_2$$ системы К , являются одновременными, если они происходят в один и тот же момент времени $$t_1=t_2(Δt=0)$$ по часам, расположенным в этих точках. При этом предполагается, что часы синхронизированы согласно определению Эйнштейна. В системе К’ эти же события произойдут в точках с координатами $$x^,_1$$ и $$x^′_2$$ в моменты времени $$t^′_1$$ и $$t^,_2$$ . Использовав преобразования Лоренца, покажем, что события, одновременные в системе К , в системе К’ будут происходить в разные моменты времени. Воспользуемся преобразованиями Лоренца (7.3.6)

Поэтому наблюдатели в системе К′ зафиксируют эти события как неодновременные $$t^,_1≠t^,_2$$ . Справедливо и обратное утверждение − события, одновременные в ИСО К′ , не одновременны в ИСО К . Это явление известно как относительность одновременности и возникает из-за ограниченности скорости распространения взаимодействий.

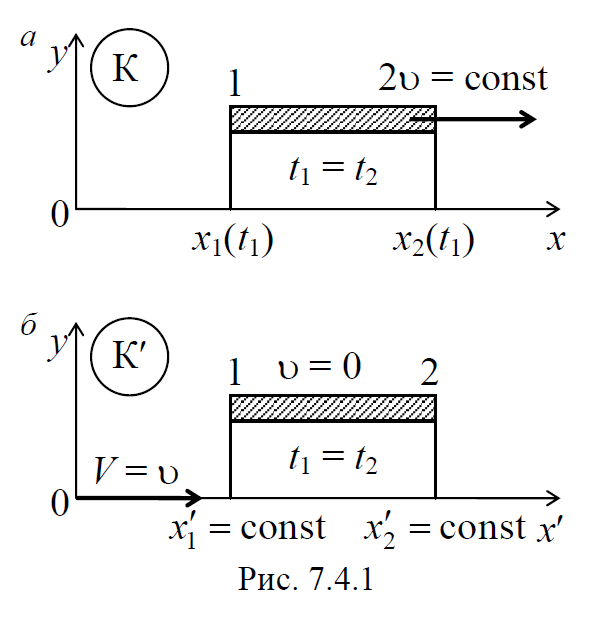
2) Сокращение длины движущихся тел . Длиной движущегося тела в некоторой системе отсчета, по определению, называется расстояние между двумя точками этой системы координат, с которыми совпадают начало и конец тела в один и тот же момент времени по часам, расположенным в этих же точках используемой системы (рис. 7.4.1). Это значит, что $$l=x_2-x_1$$ , если $$t_2=t_1$$ . В собственной системе отсчета $$K′$$ , в которой рассматриваемый объект покоится, собственная длина тела, $$l_0=x^,_2-x^,_1$$ . Воспользуемся преобразованиями Лоренца (7.3.6).

Соответственно, длина l линейки, измеренная в ИСО К , всегда меньше $$l_0$$ − так называемой собственной длины, измеренной в системе покоя линейки К′ . Это явление называется релятивистским сокращением длин и помимо данного кинематического рассмотрения может быть выведено также и динамически из изменения сил, действующих между частицами вещества при его движении.

3) Интервал времени между двумя событиями . Собственным временем $$τ_0$$ называется интервал времени между двумя событиями, которые произошли в одной и той же точке собственной системы: отсчета, связанной с движущимся со скоростью υ объектом. Это значит, что в системе К’ время $$τ_0=t^,_2=t^,_1$$ определяется при условии, что $$x^,_2=x^,_1$$ , т. е. события происходя в одной и той же точке системы К’ , которая движется равномерно и прямолинейно с скоростью υ . С учетом сказанного из преобразования Лоренца следует

7.5. Теорема сложения скоростей в СТО

Формула преобразования скоростей в СТО устанавливает связь между проекциями скорости точки в двух произвольных инерциальных системах отсчета. Пусть в системах отсчета К и К’ движение материальной точки определяется координатным способом

Тогда проекции скорости

Воспользуемся преобразованиями Лоренца (7.3.7) и продифференцируем

Выражения (7.5.4−7.5.6) являются формулами преобразования скоростей при переходе от одной системы отсчета в другую ( релятивистский закон сложения скоростей ).

Если аналогичные действия проделать с обратными преобразованиями Лоренца в форме (7.3.6), то получим выражение для скоростей в системе К′ через скорости в системе К .

Источник