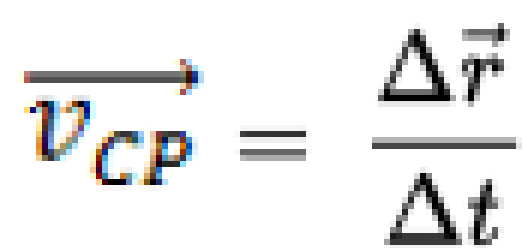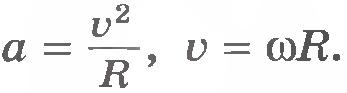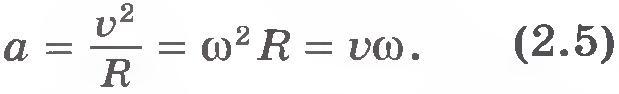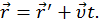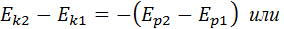Границы применимости классического способа описания движений.
В классической механике состояние движения частицы в любой момент времени характеризуется положением (координатой x при одномерном движении) и скоростью v. Вместо скорости можно пользоваться также импульсом, т.е. величиной p=mv, равной произведению массы частицы m на ее скорость. Образом частицы является геометрическая точка, описывающая с течением времени непрерывную траекторию. В квантовой механике показано, что такой способ описания движения имеет принципиальные границы применимости. Здесь преждевременно вдаваться в подробное обсуждение этого вопроса. Достаточно ограничиться предварительным сообщением основного результата, не касаясь его обоснования.
Согласно квантовой механике состояние частицы в каждый момент времени нельзя характеризовать точными значениями ее координаты и импульса в этот момент времени. Если в каком-либо состоянии координата известна с неопределенностью δx, а импульс — с неопределенностью δp, то обе эти величины одновременно не могут быть сделаны сколь угодно малыми. Они связаны соотношением
где h — универсальная постоянная, называемая постоянной Планка (1858—1947). Она играет основную роль во всех квантовых явлениях. Ее численное значение равно
Соотношение (1.5.1) называется принципом неопределенностей Гайзенберга. Оно определяет принципиальный предел точности одновременного измерения координаты и импульса частицы, который не может быть превзойден никаким усовершенствованием приборов и методов измерения. Дело здесь не в ошибках измерений. Такова уж природа реальных частиц, что мгновенные состояния их движения не могут быть охарактеризованы классически — точными значениями координат и импульсов. Частицы ведут себя более сложно, чем материальные точки классической механики. Классическая картина движения по непрерывным траекториям лишь приближенно соответствует законам природы. Границы ее применимости определяются соотношением неопределенностей (1.5.1). Из него следует, что мгновенное состояние движения частицы нельзя также характеризовать абсолютно точными значениями координаты и скорости. Неопределенности этих величин должны удовлетворять условию
Для макроскопических тел практическая применимость классического способа описания движения не вызывает сомнений. Допустим, например, что речь идет о движении шарика с массой m=1 г. Обычно положение шарика практически может быть определено с точностью до десятой или сотой доли миллиметра. Во всяком случае вряд ли имеет смысл говорить об ошибке в определении положения шарика, меньшей размеров атома. Положим поэтому δx=10−8 см. Тогда из соотношения неопределенностей (1.5.1) найдем
Одновременная малость величин δx и δv и является доказательством практической применимости классического способа описания движения для макроскопических тел. Не так обстоит дело, когда речь идет об атомных явлениях — явлениях, происходящих с частицами очень малой массы в очень малых объемах пространства. Рассмотрим, например, движение электрона в атоме водорода. Масса электрона m=9,11⋅10−28 г. Ошибка в положении электрона δx во всяком случае не должна превышать размеры атома, т.е. должно быть δx hmδx=6,63⋅10−279,11⋅10−28⋅10−8≈7⋅108 см/с.
Эта величина не меньше, а даже больше самой скорости электрона в атоме, которая по порядку величины равна 108 см/с. При таком положении классическая картина движения теряет всякий смысл.
10. Инерциальные системы отсчета –это система отсчета, в которой справедлив закон инерции: материальная точка, когда на нее не действуют никакие силы (или действуют силы взаимно уравновешенные), находится в состоянии покоя или равномерного прямолинейного движения.
Всякая система отсчета, движущаяся по отношению к инерциальной системе отсчета поступательно, равномерно и прямолинейно, есть также инерциальная система отсчета.
Следовательно теоретически может существовать любое число равноправных инерциальных систем отсчета, обладающих тем важным свойством, что во всех таких системах законы физики одинаковы (принцип относительности).
При переходе от одной инерциальной системы отсчета к другой в классической механике Ньютона для пространственных координат и времени справедливы преобразования Галилея (принцип относительности), а в релятивистской механике- преобразования Лоренца.
Считается, что система отсчета, движущаяся по отношению к инерциальной системе отсчета с ускорением, не инерциальна и закон инерции в ней не соблюдается.
Неинерциальная система отсчёта — система отсчёта, к которой не применим закон инерции (говорящий о том, что каждое тело, в отсутствие действующих на него сил, движется по прямой и с постоянной скоростью), и поэтому для согласования сил и ускорений в которой приходится вводить фиктивные силы инерции. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, является неинерциальной.
Законы Ньютона выполняются только в инерциальных системах отсчёта. Для того, чтобы найти уравнение движения в неинерциальной системе отсчёта, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной.
Классическая механика постулирует следующие два принципа:
1. время абсолютно, то есть промежутки времени между любыми двумя событиями одинаковы во всех произвольно движущихся системах отсчёта;
2. пространство абсолютно, то есть расстояние между двумя любыми материальными точками одинаково во всех произвольно движущихся системах отсчёта.
Эти два принципа позволяют записывать уравнение движения материальной точки относительно любой неинерциальной системы отсчёта, в которой не выполняется первый закон Ньютона.
Основное уравнение динамики относительного движения материальной точки имеет вид:

где 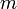
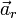
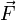


Это уравнение может быть записано в привычной форме Второго закона Ньютона, если ввести фиктивные силы инерции:
· 
· 
Векторная величина, равная произведению массы материальной точки на её ускорение и направленная противоположно ускорению, называется силой инерции
Об ычные или простые силы инерции. К ним относится два слагаемых: — одно связано с неравномерным поступательным движением, а второе – с неравномерным вращением.
Центробежная сила — составляющая фиктивных сил инерции, которую вводят при переходе из инерциальной системы отсчёта в соответствующим образом вращающуюсянеинерциальную. Это позволяет в полученной неинерциальной системе отсчёта продолжать применять законы Ньютона для расчёта ускорения тел через баланс сил
Сила Кориолиса — одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения.
Источник
Границы применимости классической механики
Вы будете перенаправлены на Автор24
Классическая механика, получившая название механики Ньютона, дает качественные характеристики закономерностей механического движения. Классическая механика описывает в универсальном стиле движение любых материальных точек. Из них во времена Исаака Ньютона можно было строить любые возможные материальные объекты во Вселенной. Таким незамысловатым образом давалось теоретическое объяснение разных механических явлений в природе. Такие закономерности были сформулированы в ряде основных постулатов тех лет и до сих пор многие из них актуальны.
Рисунок 1. Границы применимости классической механики. Автор24 — интернет-биржа студенческих работ
Постулаты классической механики
Они звучат следующим образом:
- пространство и время существуют раздельно друг от друга и не имеют прямой зависимости от материальных тел, которые находятся в физическом мире;
- само пространство можно представить в виде однородного и изотропного явления;
- формулируются законы импульса и момента импульса;
- ход времени не зависит от материальных тел, которые находятся в пространстве;
- это ведет к однородности времени, то есть формулируется закон сохранения энергии.
Рисунок 2. Постулаты классической механики. Автор24 — интернет-биржа студенческих работ
В инерциальных системах отсчета действуют иные принципы. Для таких явлений будет справедливо использовать принцип относительности, который сформулировал Галилей. Согласно его представлениям всевозможные механические процессы могут протекать в любой инерциальной системе отсчета с одинаковой точностью. В этот момент будут действовать силы взаимодействия. Они зависят от положения всех материальных точек в пространстве и времени.
Готовые работы на аналогичную тему
Таким образом, процесс взаимодействия между разными объектами физического мира будет происходить мгновенно, при этом объекты находятся на произвольном расстоянии между собой. В механике Ньютона действует бесконечно большая скорость распространения взаимодействия. Второй закон Ньютона предусматривает наличие массы материальной точки, но она не будет зависеть от показателей скорости своего движения.
Все измерения согласно представленным постулатам и законам классической механики можно провести с большой точностью. Это касается в первую очередь показателей динамических и кинетических переменных. Они представлены в виде координат, момента импульса, а также проекции импульса. Из этого следует, что можно охарактеризовать движение любой материальной частицы. Для этого представлено понятие траектории. Оно складывается из расчета выше представленных переменных.
Противоречия с электромагнетизмом
Через некоторое время подобные незыблемые правила оказались под угрозой в связи с выявлением ряда ограничений. Весь раздел классической механики Ньютона подвергся определенным ограничительным рамкам в связи с опытными изысканиями и научными трудами основоположников теории электромагнетизма. Ими выступили знаменитые ученые Максвелл и Фарадей. Они смогли исследовать экспериментальным способом различные электромагнитные явления и разработали собственные правила, применимые к ним в полной мере, отдалив основы классической механики.
С точки зрения явления электромагнетизма, существует иная нематериальная основа всех происходящих процессов с физическими телами. Открытое электромагнитное поле выступило в роли новой изучаемой материи, на которую нанизываются основы нового раздела физики. Они не могли в полной мере подчиняться ранее опубликованным трудам Исаака Ньютона о материальной основе механической физики.
Около ста лет назад были проведены достаточно точные исследования в области измерения основных величин времени и пространства. Была с большой точностью установлена скорость света. Оказалось, что она имеет свое конечное значение, которое никак не может изменяться. Это означало, что все объекты в физическом мире имеют предельную скорость распространения, так как свет был основой передачи любых сигналов и взаимодействий из одной точки пространства в другую.
Это резко контрастировало с утверждениями Галилея и его принципом относительности. Классический закон сложения скоростей экспериментальным способом был отменен. В это время начало зарождаться новое направление в физике, которое получило название релятивистской механики. После указанных опытов выявились и иные противоречия. Физическое пространство в реальном времени может обладать признаками кривизны. Оно определяется расположением масс в пространстве. Это удалось доказать во время солнечного затмения, когда измерялись показатели отклонения световых лучей, которые шли от иных звезд и распространялись прямолинейно вблизи Солнца.
Применение квантовой механики
В период создания планетарной модели элементарной частицы – атома ученый Резерфорд нашел еще одну нестыковку с классической теорией механики. Классическая физика тех лет не предполагала проблемы устойчивости атома. Эту проблему удалось решить только в середине 20 века, когда были сформулированы новые теории в рамках квантовой механики.
Рисунок 3. Применение квантовой механики. Автор24 — интернет-биржа студенческих работ
Тогда для объемного описания наблюдаемых процессов пришлось ввести величину с размерностью действия. Она смогла выступить в роли недостающего критерия применимости для описания физических явлений в классическом представлении механики Ньютона.
Изменение действия было равно произведению энергии на приращение времени, а также произведению импульса на приращение координаты. Подобное характерное изменение действия являлось соизмеримо с постоянной Планка. Оно также могло иметь меньшие показатели. Для этих случаев классическая механика была неприменима далее. Для описания и изучения физических явлений начали использовать теорию квантовой механики, которую используют и в настоящее время.
Постепенно исследователям удалось обнаружить ряд основных границ применимости законов классической механики Ньютона:
- классическая механика может быть применима только для описания механических систем, где скорость составляющих ее объектов намного меньше скорости света;
- классическая механика применима для описания таких объектов, где динамические величины с размерностью действия намного больше постоянной Планка.
Источник
Границы применимости классической механики
Вопрос 1
Физика — Наука, изучающая общие свойства материального мира, свойства и строение материи, формы ее движения и изменения.
Материя — физическое понятие, связанное с любыми объектами, существующими в природе, о которых можно судить благодаря ощущениям. Физика описывает материю как нечто, существующее в пространстве и во времени; либо как нечто, само задающее свойства пространства и времени. Изменения во времени, происходящие с различными формами материи, составляют физические явления. Основной задачей физики является описание свойств тех или иных видов материи.
Механическим движениемтела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.
Раздел механики, описывающий геометрические свойства движения без учёта причин, его вызывающих, называется кинематикой.
Границы применимости классической механики
В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность
· Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий. Другими словами, для описания свойств атомов и субатомных частиц является квантовая механика.
· При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности.
· Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц (или же большим числом степеней свободы). В этом случае практически целесообразно переходить к статистической физике.
Кинематика — раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.)
(1)Система отсчёта — это совокупность тела отсчёта, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение каких-либо тел.
(2)Система отсчет –это совокупность тела отсчета, связанных с ним координат и синхронизированных между собой часов.
Математическое движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями
Материальная точка (частица) — простейшая физическая модель в механике — обладающее массой тело, размерами, формой, вращением и внутренней структурой которого можно пренебречь в условиях исследуемой задачи. Положение материальной точки в пространстве определяется как положение геометрической точки
Поступательным движение называется такое движение абсолютно твердого тела, при котором любая прямая, жестко связанная с телом, перемещается параллельно самой себе. Все точки тела, движущегося поступательно, в каждый момент времени имеют одинаковые скорости и ускорения, а их траектории полностью совмещаются при параллельном переносе. Поэтому кинематическое рассмотрение поступательного движения абсолютно твердого тела сводится к изучению движения любой его точки.
Вращательное движение — Движение абсолютно твердого тела, при котором две его точки А и B остаются неподвижными, называется вращением (вращательнымдвижением) вокруг неподвижной прямой АВ, называемой осью вращения. При вращении твердого тела вокруг неподвижной оси все его точки описывают окружности, центры которых лежат на оси вращения, а плоскости — перпендикулярны к ней. Тело, вращающееся вокруг неподвижной оси, обладает одной степенью свободы: его положение полностью определяется заданием угла f поворота из некоторого начального положения.
Вопрос 2
Радиус-вектор — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Перемещение — вектор, соединяющий начальную и конечную точки траектории. По сути перемещение – это сумма двух радиус-векторов, конечного и начального.

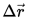
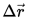
Мгновенная скорость(скорость в данный момент времени) –физическая величина, равная пределу к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Модуль вектора скорости равен отношению приращения длины пути к соответствующему промежутку времени: 
Через декартовую систему координат:


Кинематическое описание движения материальной точки.Материальной точкой называется тело, размерами и формой которого можно пренебречь в данной задаче. В декартовой системе координат положение материальной точки A в определенный момент времени, задается тремя координатами X,Y,Z или радиус-вектором 
или в векторной форме:

Траектория – это линия, вдоль которой движется тело.
Путь– скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени.
Вопрос 3

(формула в вопросе №2)

Равномерное прямолинейное движение − это движение с постоянной по модулю и направлению скоростью, при котором материальная точка совершает равные перемещения за равные промежутки времени. При прямолинейном движении траектория является прямой линией. Если направить ось X вдоль траектории, то проекции перемещения и скорости на оси Y, Z равны нулю и зависимости координаты х и модуля перемещения (в данном случае − пути) от времени для этого типа движения имеют вид: x = x0 + vхt = x0 + vt
Равноускоренное прямолинейное движение — это такое движение, при котором скорость тела за равные промежутки времени изменяется одинаково, другими словами, это движение с постоянным ускорением.
Ускорение a=const (по модулю и по направлению).
Скорость тела меняется по закону v=v0+at
Закон движения в случае равноускоренного
движения имеет вид:






Эти уравнения называются кинетическими уравнениями движения точки
Вопрос 4
Ускорение в декартовой системе координат: 
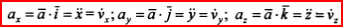



Равноускоренное движение — движение с постоянным ускорением (a = const); движение, при котором за равные промежутки времени скорость меняется одинаково (по величине и направлению).
Полное, тангенциальное и нормальное ускорения. При криволинейном движении полное ускорение материальной точки раскладывается на две составляющих: нормальное ускорение 



(1)Тангенциальное ускорение — ускорение, направленное параллельно мгновенной скорости и изменяющее ее по величине
(2)Тангенциальное (касательное) ускорение – компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости в отличие от нормальной компоненты, характеризующей изменение направления скорости. Тангенциальное ускорение равно произведению единичного вектора, направленного по скорости движения, на производную модуля скорости по времени. Таким образом, направлено в ту же сторону, что и вектор скорости при ускоренном движении (положительная производная) и в противоположную при замедленном (отрицательная производная).

Величина тангенциального ускорения связана с величиной углового ускорения соотношением:
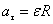

Нормальное ускорение (центростремительное ускорение) — компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной. Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделённому на радиус кривизны. Термин «центростремительное ускорение» эквивалентен термину «нормальное ускорение». Ту составляющую суммы сил, которая обуславливает это ускорение, называют центростремительной силой.
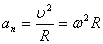
Радиус кривизны — величина, обратная кривизне. Радиус кривизны характеризует величину соответствия кривой от прямой. Чем больше радиус кривизны, тем больше кривая похожа на прямую.
Радиус кривизны определяется для конкретной точки конкретной кривой он равняется радиусу соприкасающейся окружности.
Вопрос 5
Вращательным движением абсолютно твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела движутся в плоскостях, перпендикулярных к неподвижной прямой, называемой осью вращения, и описывают окружности, центры которых лежат на этой оси.
Угловой скоростью вращения называется вектор, численно равный первой производной угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:
Связь мгновенной угловой скорости ω связана с угловым ускорением ε :
Единица измерения угловой скорости радиан в секунду (рад/с). Таким образом, вектор ω определяет направление и быстроту вращения. Если ω=const, то вращение называется равномерным.
При равномерном вращении его можно охарактеризовать периодом вращения Т –временем, за которое точка тела совершает один полный оборот, т.е. поворачивается на угол 2π (360 градусов):
Число полных оборотов, совершаемых телом при равномерном движении по окружности, в единицу времени называется частотой вращения:
Связь между линейной и угловой скоростями. Точка, лежащая на окружности радиусом R, за один оборот пройдет путь 
Так как 
Модуль ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:
Вопрос 6
Динамика — раздел механики, в котором изучаются причины возникновения механического движения.
Инерция— свойство тел оставаться в некоторых системах отсчёта в состоянии покоя или равномерного прямолинейного движения в отсутствии или при взаимной компенсации внешних воздействий.
Инерциальная система отсчёта — система отсчёта, в которой все свободные тела движутся прямолинейно (вдоль одной прямой) и равномерно (с постоянной скоростью).
(1)Первый закон Ньютона– В инерциальной системе отсчета скорость тела = const, если на тело не действуют силы (другие тела) или сумма этих сил = 0. В неинерциальной системе отсчета 1 закон Ньютона не выполняется.
(2)Первый закон Ньютона — существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения.
Инертность — свойство тела в большей или меньшей степени препятствовать изменению своей скорости относительно инерциальной системы отсчёта при воздействии на него внешних сил.
Масса — мера инертности тела (сопротивления воздействию).
Свойства массы:
1) Величина аддитивная (т.е. сумма системы = сумме масс, её составляющих)
2) Масса тела постоянна. (т.е. не изменяется при движении)
Сила — векторная физическая величина, являющаяся мерой воздействия на данное тело других тел
Равнодействующая сила – это сила, действие которой заменяет действие всех сил, приложенных к телу. Или, другими словами, равнодействующая всех сил, приложенных к телу, равна векторной сумме этих сил.
Вопрос 7
Динамика— раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия. Динамика — количественное описание взаимодействия тел, определяющего характер их движения.
Сила — это физическая величина, характеризующая изменение скорости движения тела. Она носит векторный характер, т. е. выражается вектором. Иначе сила — это скорость изменения импульса тела F = dP / dt, P = mv — импульс тела, m — масса тела, v — скорость, с которой движется тело.
Если на данное тело действует одновременно несколько сил, то их действие на движение тела можно заменить действием одной силы). Такую замену называют сложением сил. Данные силы называют слагающими или составляющими, а заменяющую их силу — их суммой или равнодействующей. Равнодействующая уравновешивающихся сил, например, двух сил, равных по величине и противоположных по направлению, равна нулю.
(1)Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).
(2)Второй закон Ньютона В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.
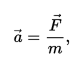
a – ускорение материальной точки; F — равнодействующая всех сил, приложенных к материальной точке; m — масса материальной точки.
Третий закон Ньютона.Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
Основное уравнение динамики материальной точкив случае,
когда на точку действуют n сил, имеет вид:
Вопрос 9
Принцип относительности Галилея:Механические явления протекают одинаково во всех инерциальных системах отсчета, т. е. описывающие их законы динамики одинаковы. Поэтому все инерциальные системы отсчета равноправны.
Это значит, что уравнения, выражающие законы механики, не меняются при преобразованиях Галилея.

Для координаты x это выражается так:
Здесь 



В любой последующий момент времени положение некоторой точки А, движущейся относительно обеих систем координат, определяется в системе K радиус-вектором 


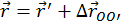

Из этого уравнения вытекает закон сложения скоростей:
где 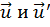
Галилей на основании наблюдений сформулировал классический принцип относительности, согласно которому законы механики одинаковы в любых инерциальных системах отсчета. То есть, уравнения движения относительно любых инерциальных систем совпадают друг с другом. Это значит, что уравнение ma = F эквивалентно уравнению m´a´ = F´.
Из принципа Галилея следует, что F = F´, т. е. силы, действующие на точку, неизменны при переходе от одной инерциальной системы к другой, также инерциальной системе.
Следовательно, все величины, входящие в уравнение Ньютона, не изменяются при преобразовании от одной инерциальной системы к другой инерциальной системе.
Вопрос 9
Вес − это сила, с которой любое тело вследствие притяжения Земли действует на опору или подвес.
Вес тела − векторная физическая величина, которую обозначают буквой P. Вес покоящегося, а также равномерно и прямолинейно движущегося (относительно Земли) тела по своему численному значению равен действующей на него силе тяжести:
где m − масса, g − ускорение свободного падения.
Сила тяжести — сила, действующая на любое материальное тело, находящееся вблизи поверхности Земли или другого астрономического тела.
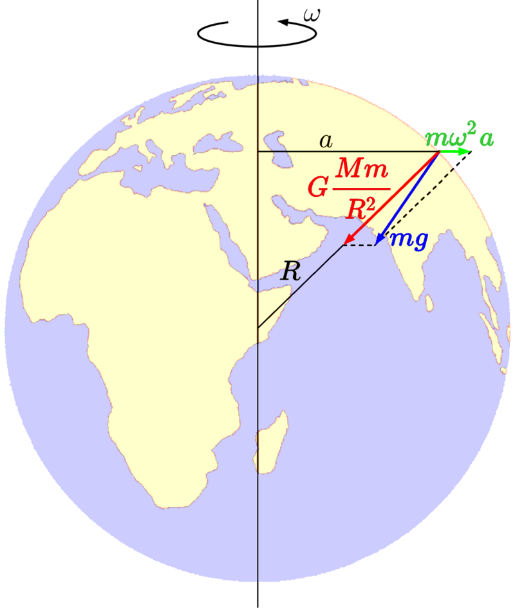
По определению, сила тяжести на поверхности планеты складывается из гравитационного притяжения планеты и центробежной силы инерции, вызванной суточным вращением планеты.
Вес и сила тяжести приложены к разным объектам: вес P приложен к опоре или подвесу, а сила тяжести Fт − к телу.
Вес и сила тяжести имеют различную физическую природу. Сила тяжести возникает вследствие взаимодействия тела и Земли. Вес тела возникает в результате взаимодействия тела и опоры (подвеса). Опора (подвес) при этом деформируется, что приводит к появлению силы упругости. Из третьего закона Ньютона следует, что вес тела, то есть сила, с которой тело давит на опору (или растягивает подвес), совпадает по величине с силой, действующей со стороны опоры на данное тело. Сила, с которой опора давит на находящееся на ней тело, называется силой реакции опоры. Обозначив силу реакции опоры N, мы можем записать:
Полученная формула является более общей, чем P=mg, так как она справедлива и в том случае, когда тело вместе с опорой совершает ускоренное движение.
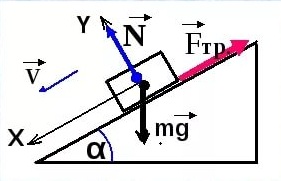
Силой трения называют силу, которая возникает при движении одного тела по поверхности другого. Трение по-другому называют фрикционным воздействием. Сила трения всегда направлена противоположно направлению движения. Сила трения прямо пропорциональна силе нормального давления на трущиеся поверхности и зависит от свойств этих поверхностей.
Сухое трение возникает между поверхностями твердых тел в отсутствие смазки.
Сухое трение, в свою очередь, подразделяется на трение скольжения и трение качения.
Установлено, что максимальная сила трения покоя не зависит от площади соприкосновения тел и приблизительно пропорциональна модулю силы нормального давления N:
μ0 – коэффициент трения покоя, зависящий от природы и состояния трущихся поверхностей.
Когда модуль внешней силы, а, следовательно, и модуль силы трения покоя превысит значение F0, тело начнет скользить по опоре – трение покоя Fтр.пок сменится трением скольжения Fск:
| Fтр = μ N, |
где μ – коэффициент трения скольжения.
Трение качения возникает между шарообразным телом и поверхностью, по которой оно катится. Сила трения качения подчиняется тем же законам, что и сила трения скольжения, но коэффициент трения μ ; здесь значительно меньше.
Коэффициент трения — количественная характеристика силы, необходимой для скольжения или движения одного материала по поверхности другого. Если обозначить вес предмета как N, а коэффициент трения — m, то сила (F), необходимая для движения предмета по ровной поверхности без ускорения, равна F = mN. Коэффициент трения покоя определяет силу, необходимую для начала движения; коэффициент кинетического трения (трения движения) определяет (меньшую) силу, необходимую для поддержания движения.
Вопрос 10
Импульсом материальной точки называют величину равную произведению массы точки на ее скорость. Обозначим импульс буквой p⃗. Тогда p⃗ = mυ⃗. Из этой формулы видно, что импульс — векторная величина.
Импульс системы P∑→ материальных точек массами m1, m2, m3, …, имеющих скорости V1→, V2→, V3→, …, определяется соотношением: P∑→=m1V1→+m2V2→+m3V3→+…,то есть P∑→=P1→+P2→+P3→+…, где Pk→ — импульс k-й материальной точки. Т.е. это сумма импульсов материальных точек этой системы.
Система называется замкнутой, если на неё не действуют внешние силы или сумма внешних сил = 0.
Вопрос 11

Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую. В механике принято говорить, что работа совершается силой.
Работа силы на конечном перемещении равна сумме ее работ на элементарных участках.
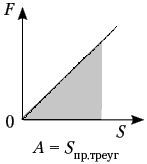
Работа силы на перемещении М1М2 изображается площадью фигуры, ограниченной осью абсцисс, кривой и ординатами, соответствующими точкам М1 и М0.
Единица измерения работы силы и кинетической энергии в системе СИ 1 (Дж).

Если F = const, то
Работой 
называется физическая величина, равная произведению модулей
силы и перемещения, умноженному на косинус угла 
Выражение показывает, что работа является скалярной величиной и может иметь положительное или отрицательное значение в зависимости от знака косинуса угла 
Работа, совершаемая силой 



Работа силы упругости — работа, совершаемая силой упругости при изменении деформации пружины от некоторого начального значения x1 до конечного значения x2
Вывод формулы работы силы упругости (через интеграл)

Найдем работу, совершаемую силами поля тяготения, созданного точечной массой М, при перемещении материальной точки с массой m. Силы тяготения являются консервативными силами, поэтому их работа не зависит от траектории, а лишь от начального и конечного положения тела. Работа сил тяготения по перемещению тела на малый вектор dr вдоль линии, соединяющей два тела, равна:

Вопрос 12
Мощность— физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. P=N=W ß буквы взаимозаменяемы.


P= 


= Вт [ватты] скалярная физическая величина.
Кинетическая энергия — скалярная функция, являющаяся мерой движения материальной точки и зависящая только от массы и модуля скорости материальных точек, образующих рассматриваемую физическую систему[1], энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта. Часто выделяют кинетическую энергию поступательного и вращательного движения[2].
Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением[3].
Простым языком, кинетическая энергия — это энергия, которую тело имеет только при движении. Когда тело не движется, кинетическая энергия равна нулю.
dA = F dr =m * 
dA=d( 

Вопрос 13
Полем сил называют область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке (поле силы тяжести Земли). Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения частицы.
Стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от траектории, а зависит только от положения этих точек, называется потенциальным, а сами силы – консервативными (F тяж, F упр).
Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называют неконсервативными (F трения).
Свойства консервативных сил:
1) 
2) 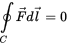
3) 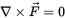
4) 
Таким образом, потенциальная сила всегда направлена в сторону уменьшения потенциальной энергии.
Вопрос 14
Билет 15
Полная механическая энергия частицы – энергия механического движения и взаимодействия, равная сумме кинетической и потенциальной энергий: E = Ek + Ep.
Приращение Ек или Т равно элементарно работе результирующей Fрез всех сил. В стационарном поле это консервативная сила этого поля Fконс и иные силы Fстор. à Fрез = Fконс + Fстор. Робота этих сил идет на приращение кинетической энергии частицы:
Т.к. работа равна убыли потенциальной энергии Аконс = — ΔU, то подставив это в выражение, после преобразований получим:
Отсюда видно, что работа сторонних сил идет на приращение величины T+U, что и есть полная механическая энергия.
Закон сохранения.
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:
Билет 16
Кинетическая энергия механической системы — это энергия механического движения рассматриваемой системы. Обозначается как Ек или Т.
Теорема о кинетической энергии системы— одна из общих теорем динамики, является следствием законов Ньютона. Связывает кинетическую энергию механической системы с работой сил, действующих на тела, составляющие систему. В качестве системы, о которой идёт речь, может выступать любая механическая система, состоящая из любых тел.
Кинетической энергией системы называют сумму кинетических энергий всех тел, входящих в систему. Для определённой таким образом величины справедливо утверждение:
Изменение кинетической энергии системы равно работе всех внутренних и внешних сил, действующих на тела системы.
Рассмотрим систему материальных точек с массами mi, скоростями vi и кинетическими энергиями Ti=1/2(mivi 2 ). Для малого изменения кинетической энергии (дифференциала), происходящего в течение некоторого малого промежутка времени dt будет выполняться:
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Источник