- Графы. Применение графов к решению задач
- 1. Методические рекомендации к теме “Графы”.
- 2. Теоретический материал к теме “Графы”.
- 3. Задачи к теме “Графы”
- Теория графов. Основные понятия и виды графов
- Теория графов
- Основные понятия теории графов
- Путь и цепь в графе
- Визуализация графовых моделей
- Виды графов
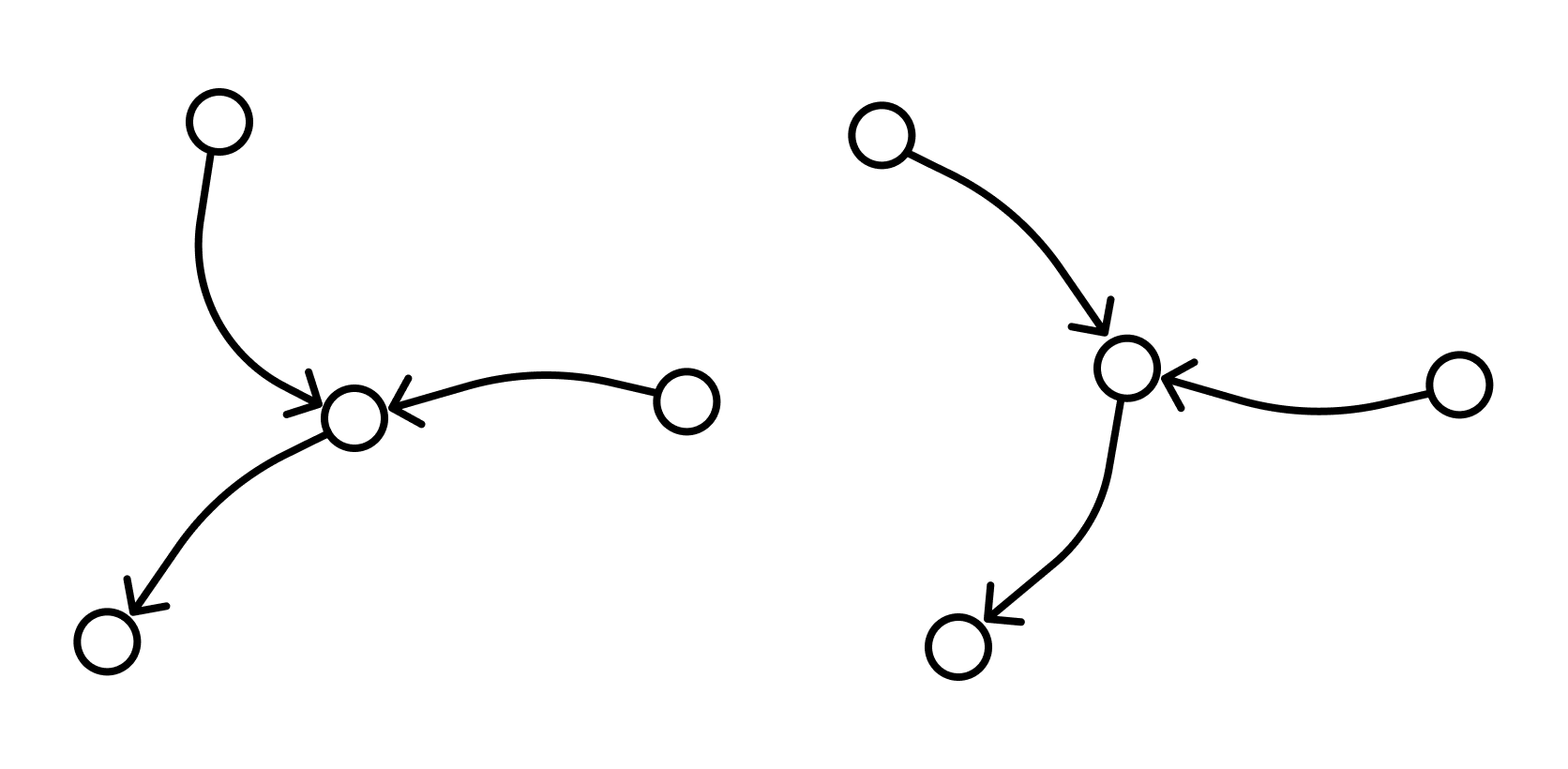
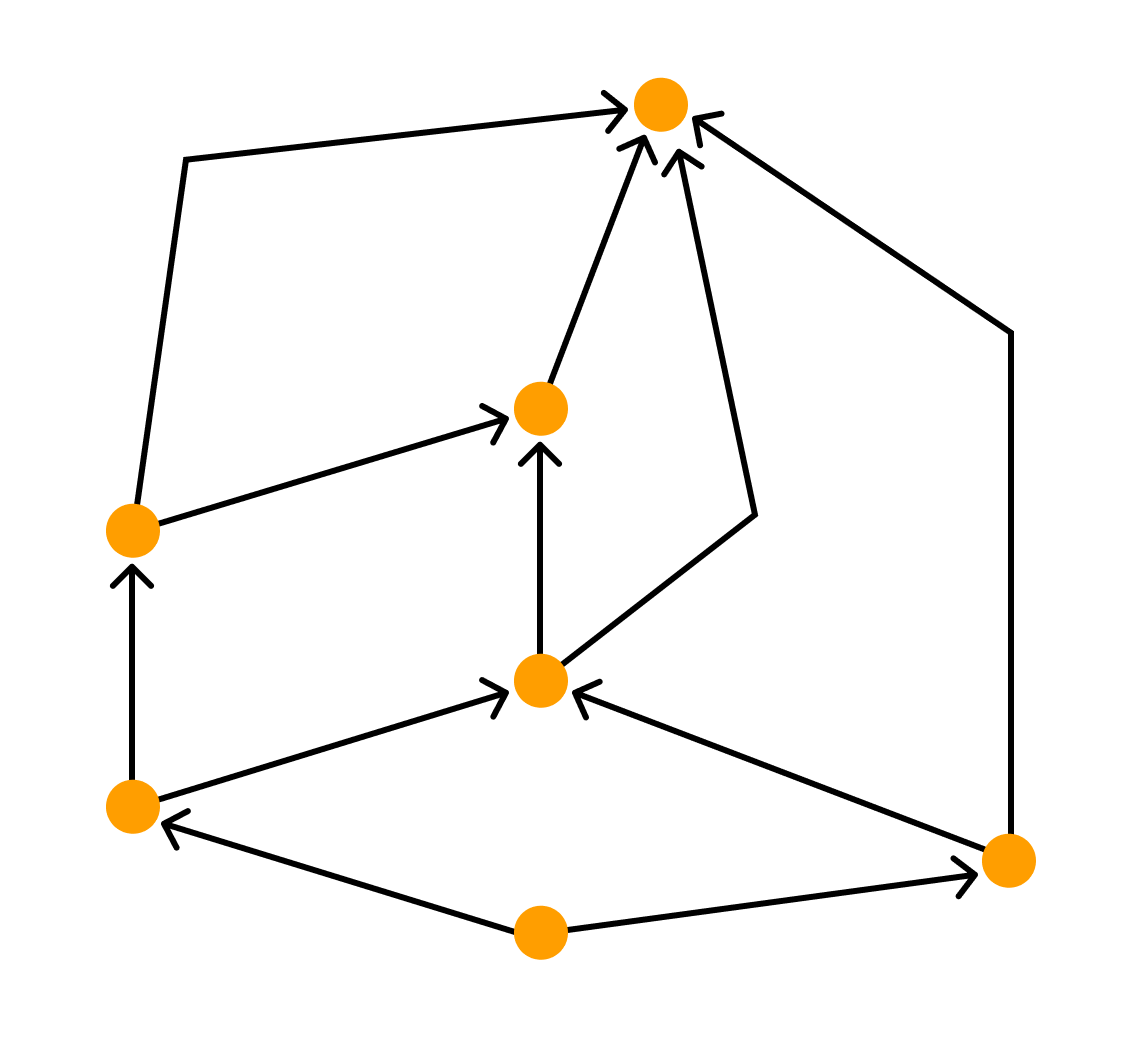
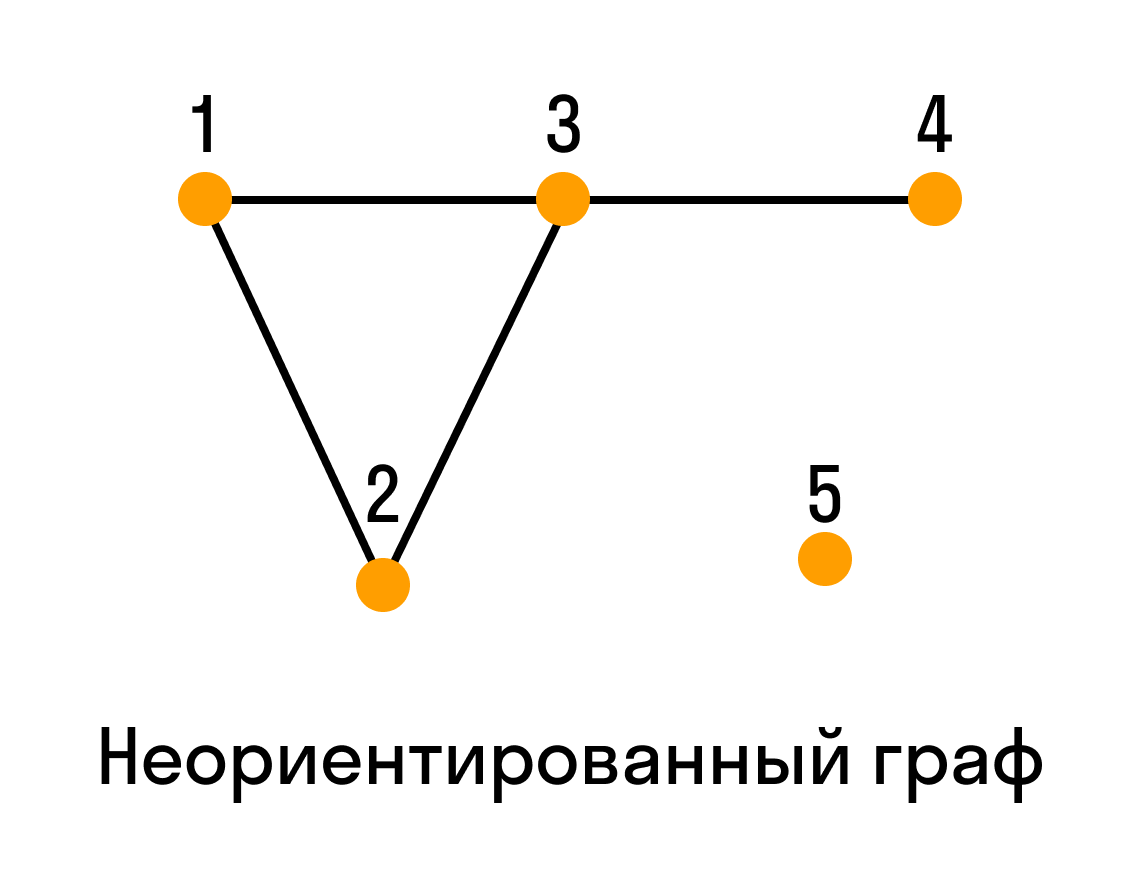
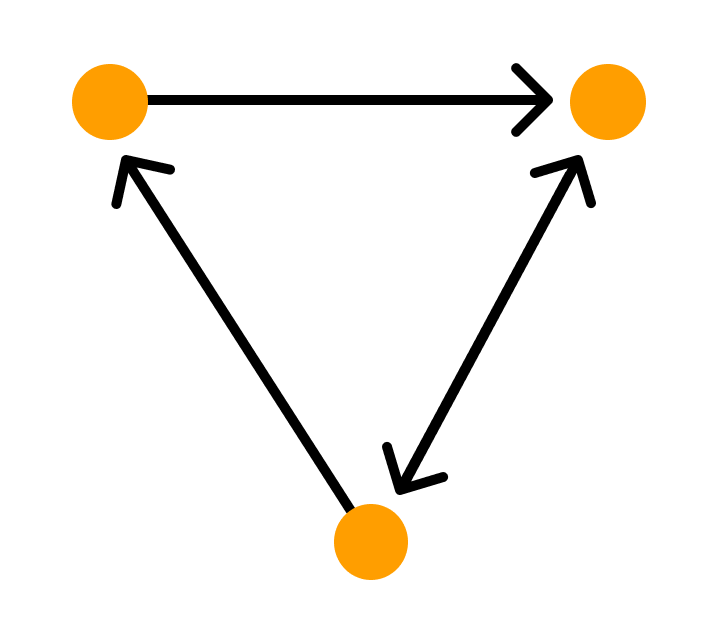
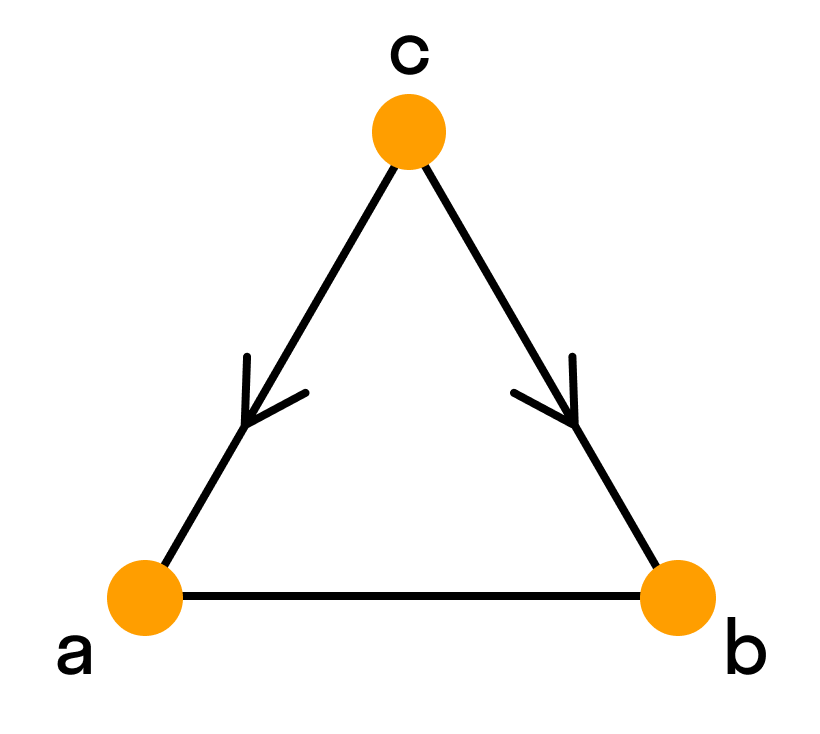
- Ориентированные и неориентированные графы
- Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы
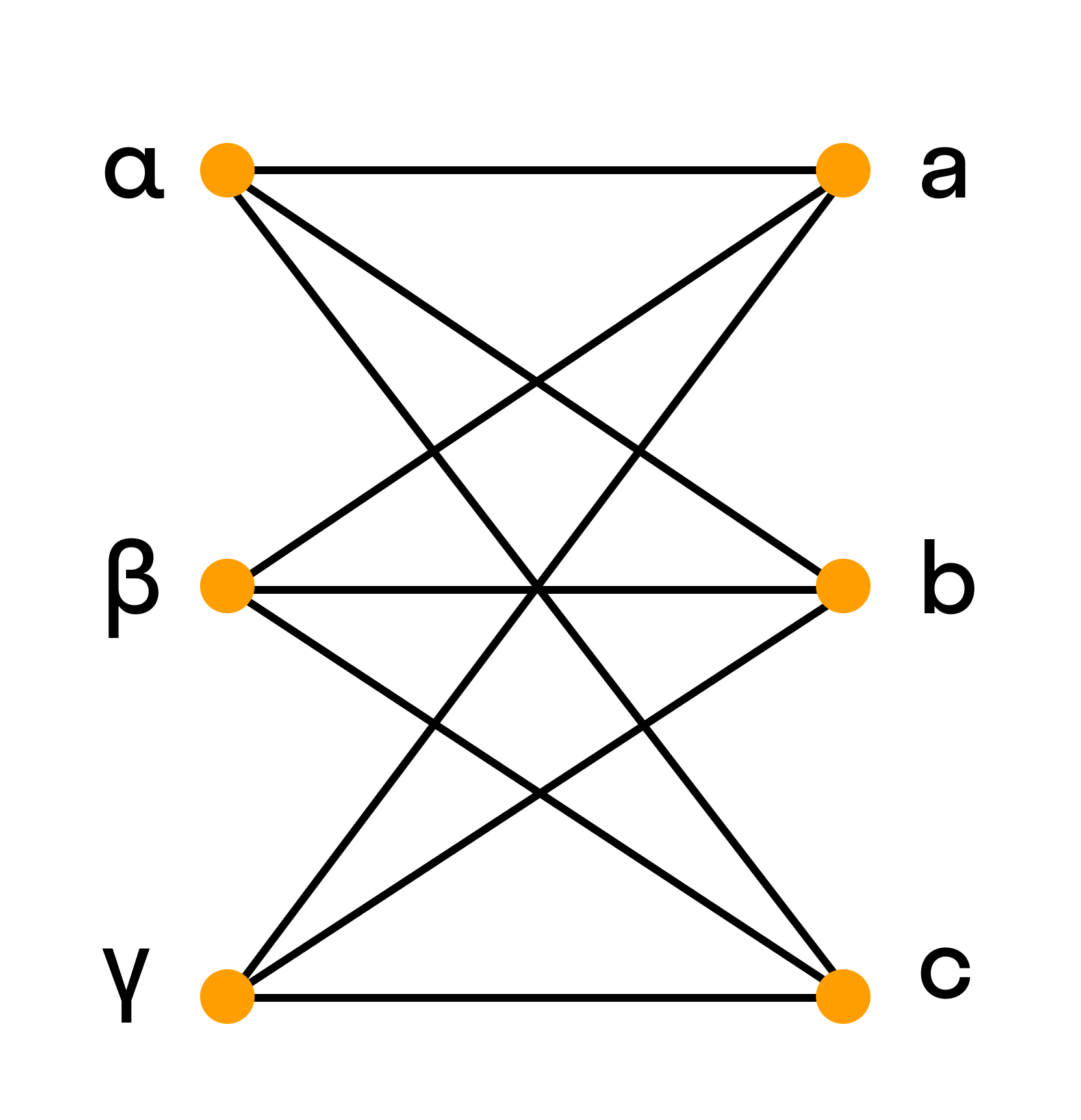
- Двудольный граф
- Эйлеров граф
- Регулярный граф
- Гамильтонов граф
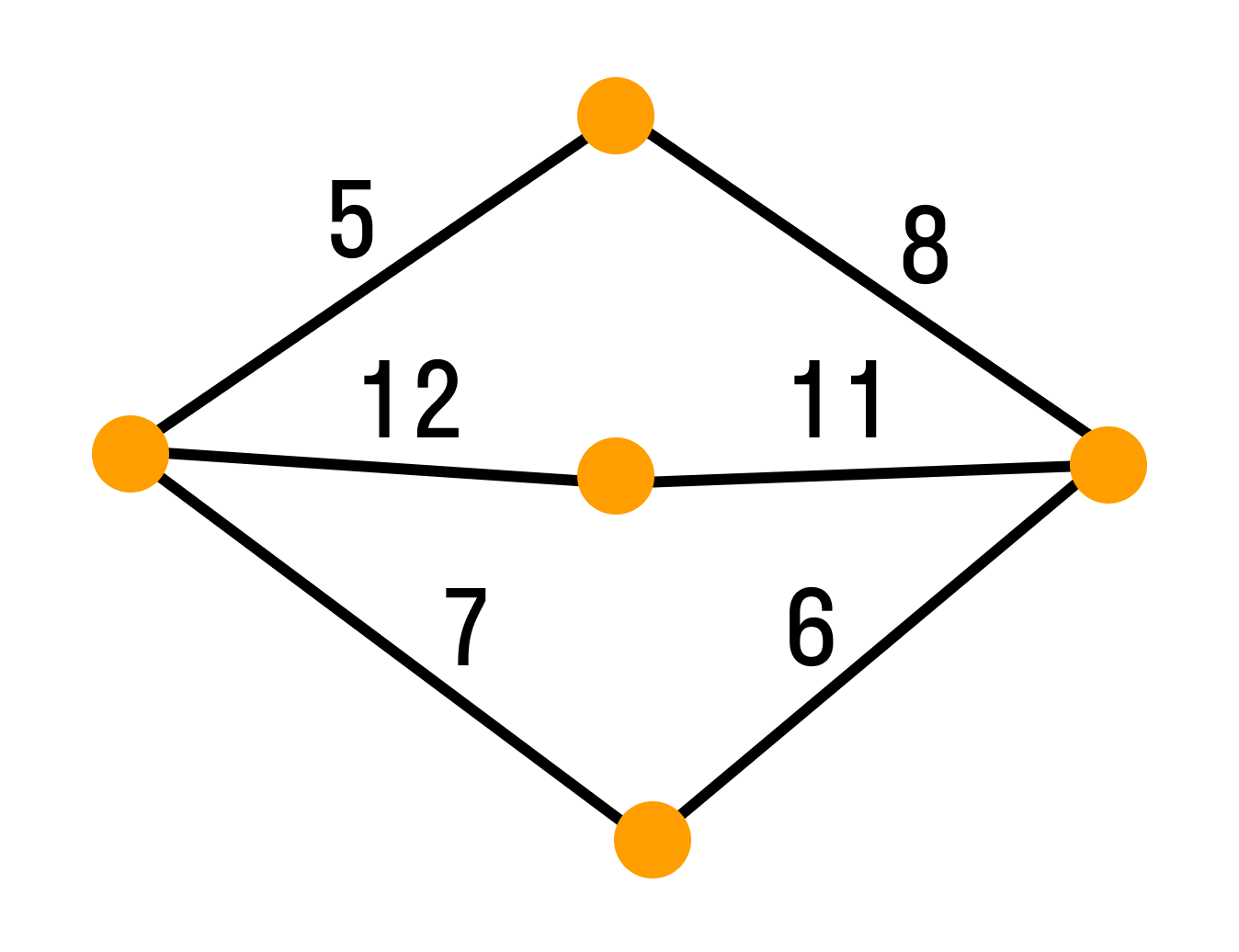
- Взвешенный граф
- Графы-деревья
- Определение дерева
- Теоремы дерева и их доказательства
- Теория графов и современные прикладные задачи
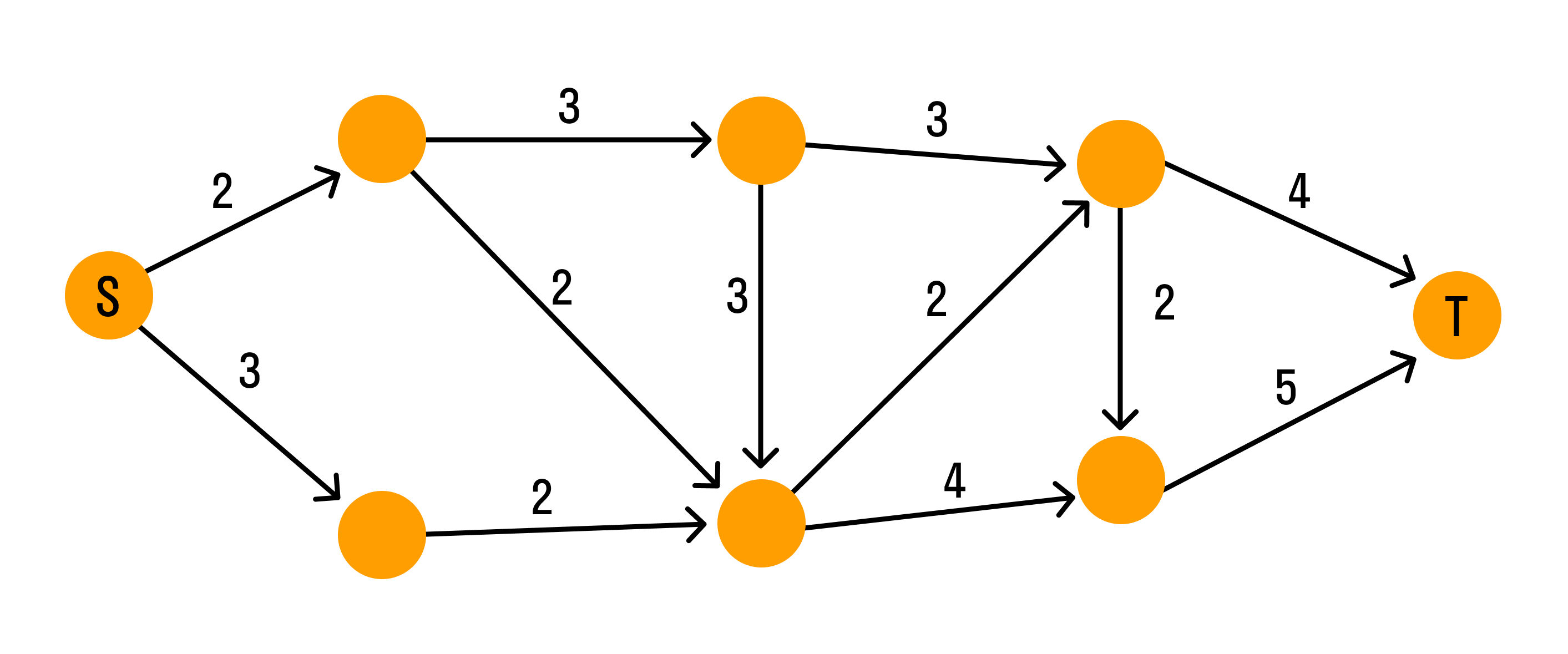
- Графы и задача о потоках
- Графы и сетевое планирование
Графы. Применение графов к решению задач
1. Методические рекомендации к теме “Графы”.
Понятие графа целесообразно вводить после того, как разобрано несколько задач, подобных задаче 1, решающее соображение в которых – графическое представление. Важно, чтобы ученики сразу осознали, что один и тот же граф может быть нарисован разными способами. Строгое определение графа, на мой взгляд, давать не нужно, т.к. оно слишком громоздко и это только затруднит обсуждение. На первых порах хватит и интуитивного понятия. При обсуждении понятия изоморфизма можно решить несколько упражнений на определение изоморфных и неизоморфных графов. Одно из центральных мест темы – теорема о четности числа нечетных вершин. Важно, чтобы ученики до конца разобрались в ее доказательстве и научились применять к решению задач. При разборе нескольких задач рекомендую не ссылаться на теорему, а фактически повторять ее доказательство. Чрезвычайно важно также понятие связности графа. Содержательным соображением здесь является рассмотрение компоненты связности, на это необходимо обратить особое внимание. Эйлеровы графы – тема почти игровая.
Первая и главная цель, которую нужно преследовать при изучении графов, –научить школьников видеть граф в условии задачи и грамотно переводить условие на язык теории графов. Не стоят рассказывать обе всем на нескольких занятиях подряд. Лучше разнести занятия по времени на 2–3 учебных года. (Прилагается разработка занятия “Понятие графа. Применение графов к решению задач” в 6 классе).
2. Теоретический материал к теме “Графы”.
Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение. Мы же обсудим только самые основные понятия, свойства графов и некоторые способы решения задач.
Рассмотрим две задачи.
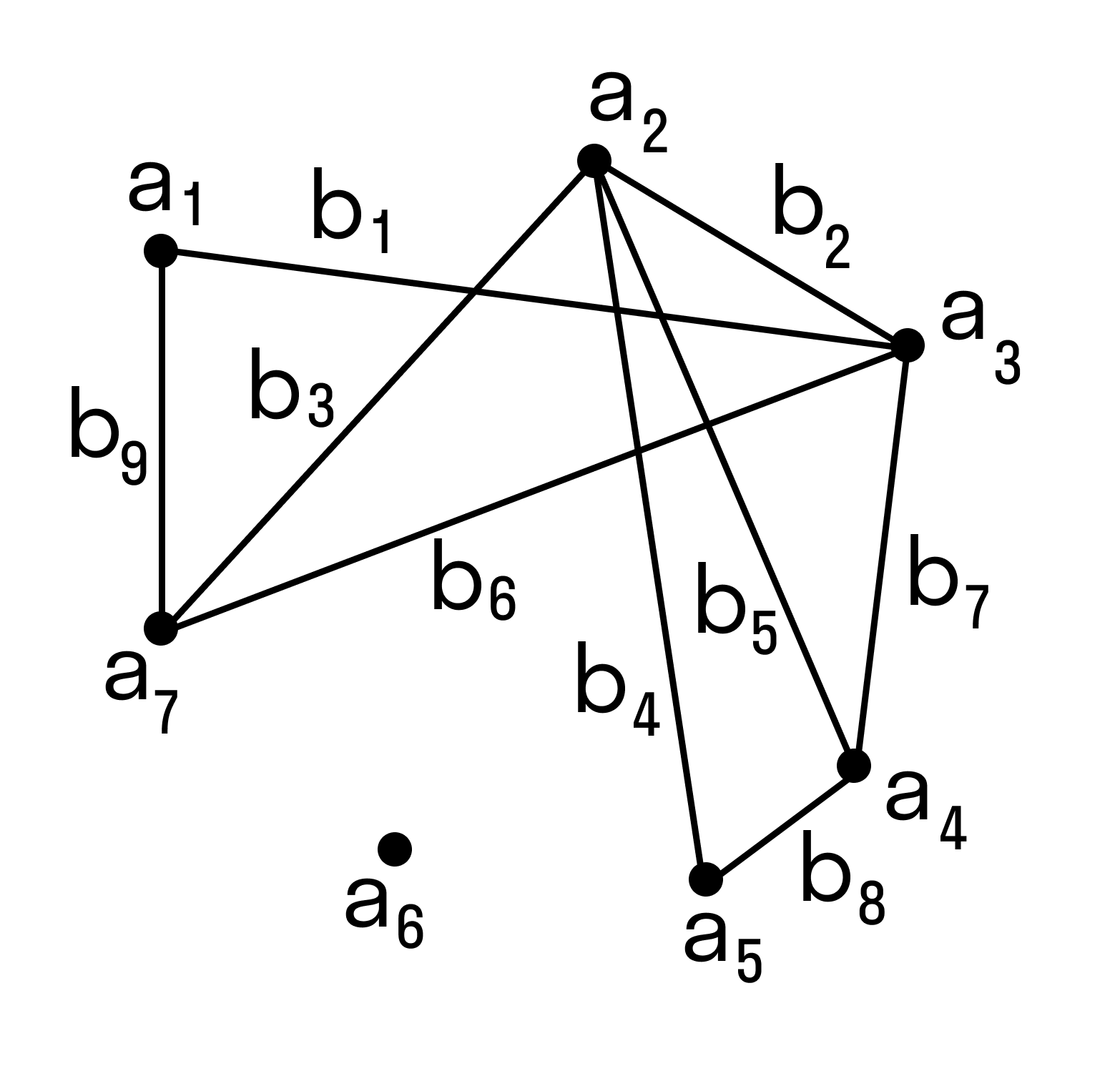
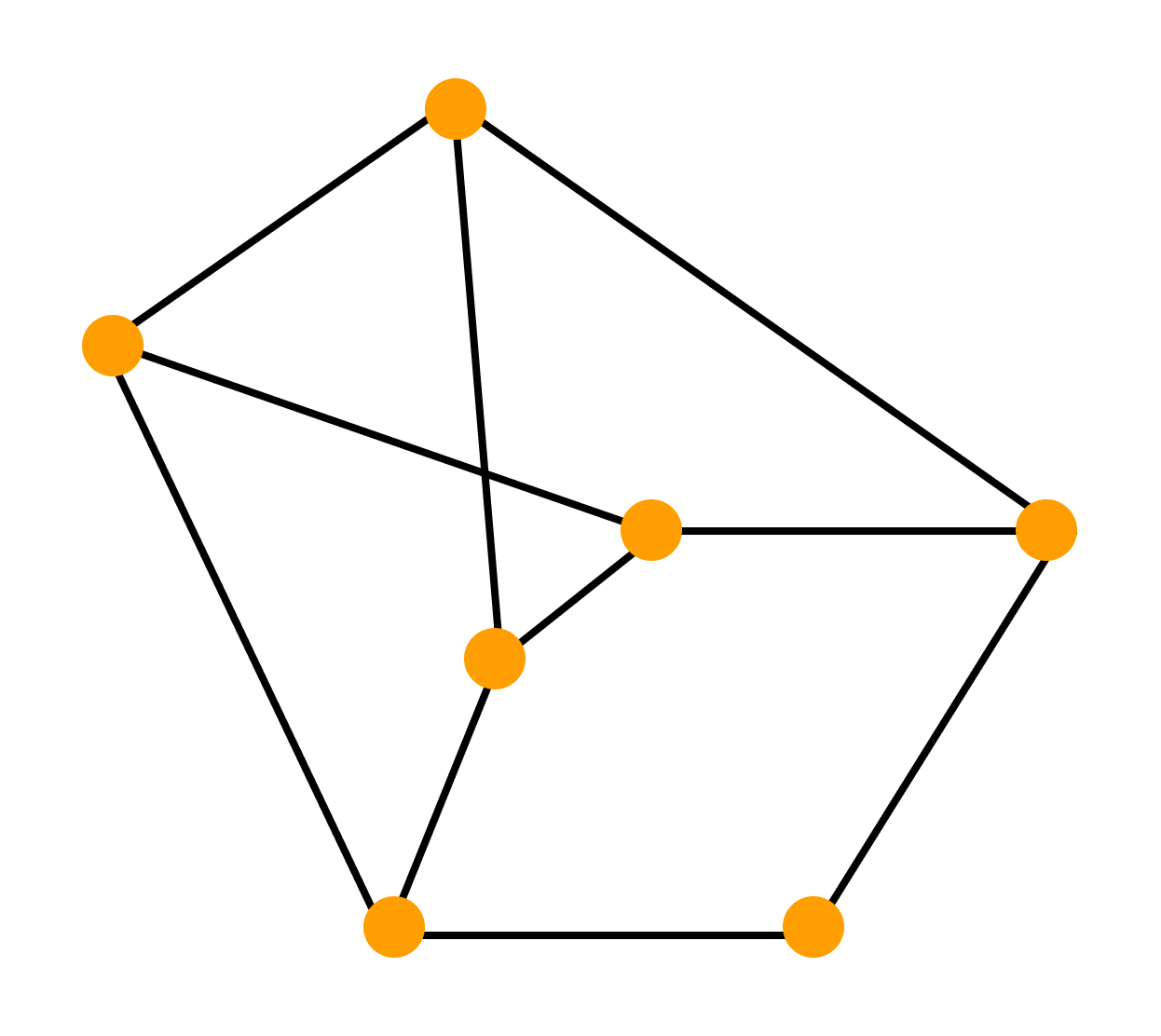
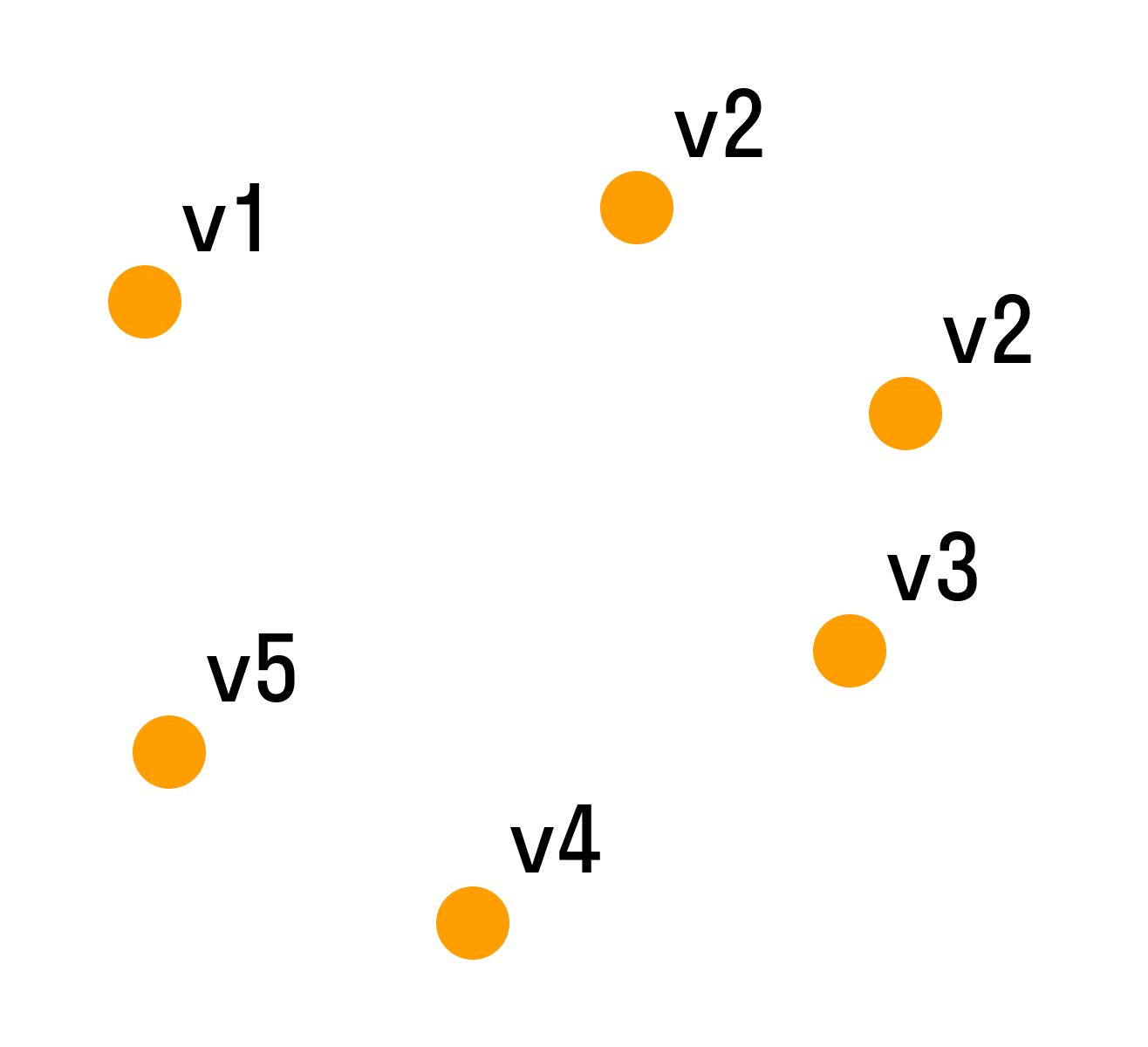
Задача 1. Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?
Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.
Теперь сразу видно, что долететь с Земли до Марса нельзя.
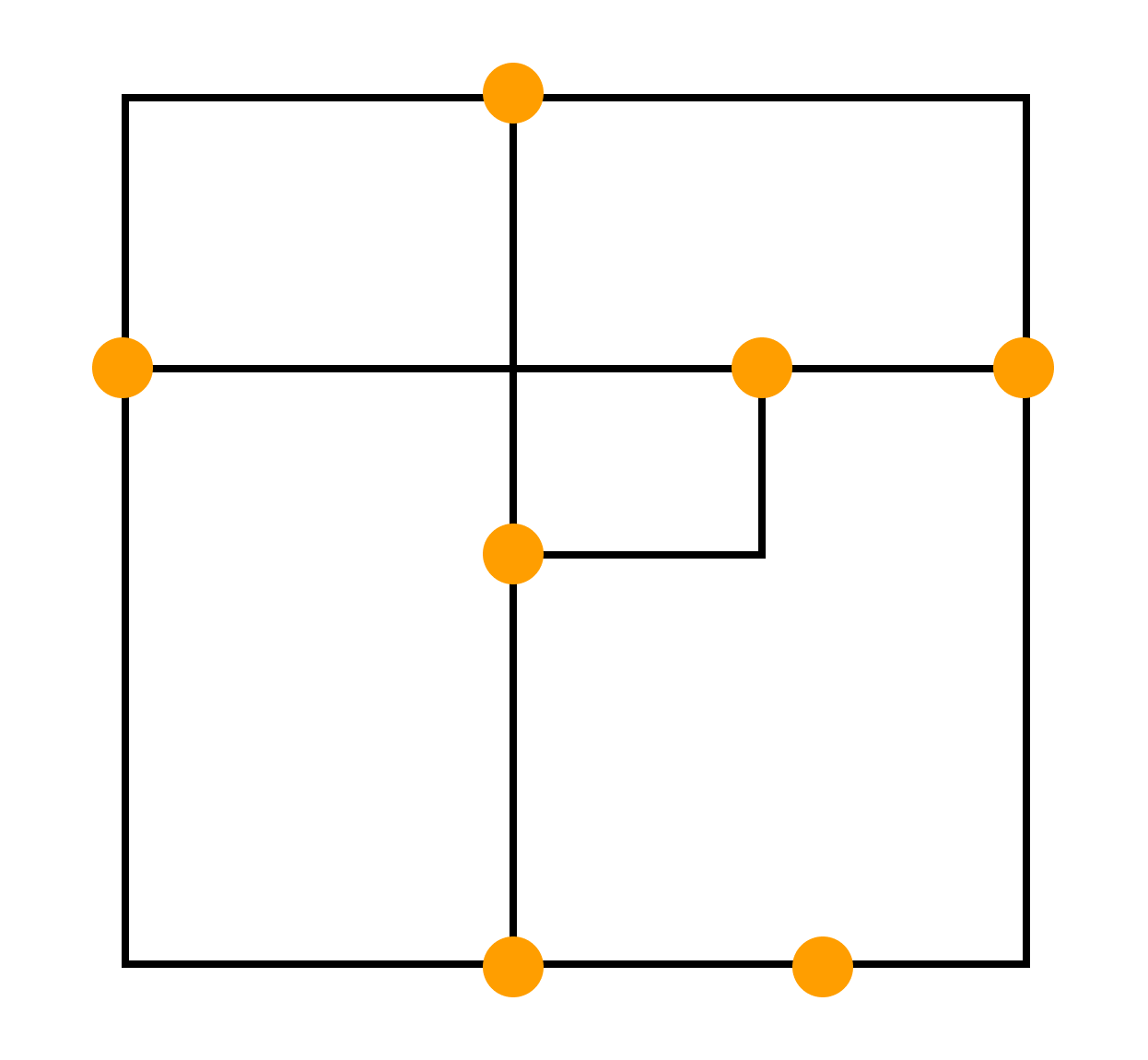
Задача 2. Доска имеет форму двойного креста, который получается, если из квадрата 4×4 убрать угловые клетки.
Можно ли обойти ее ходом шахматного коня и вернуться на исходную клетку, побывав на всех клетках ровно по одному разу ?
Решение: Занумеруем последовательно клетки доски:
А теперь с помощью рисунка покажем, что такой обход таблицы, как указано в условии, возможен:
Мы рассмотрели две непохожие задачи. Однако решения этих двух задач объединяет общая идея – графическое представление решения. При этом и картинки, нарисованные для каждой задачи, оказались похожими: каждая картинка – это несколько точек, некоторые из которых соединены линиями.
Такие картинки и называются графами. Точки при этом называются вершинами, а линии – ребрами графа. Заметим, что не каждая картинка такого вида будет называться графом. Например. если вас попросят нарисовать в тетради пятиугольник, то такой рисунок графом не будет. Будем называть что рисунок такого вида, как в предыдущих задачах, графом, если есть какая-то конкретная задача для которой такой рисунок построен.
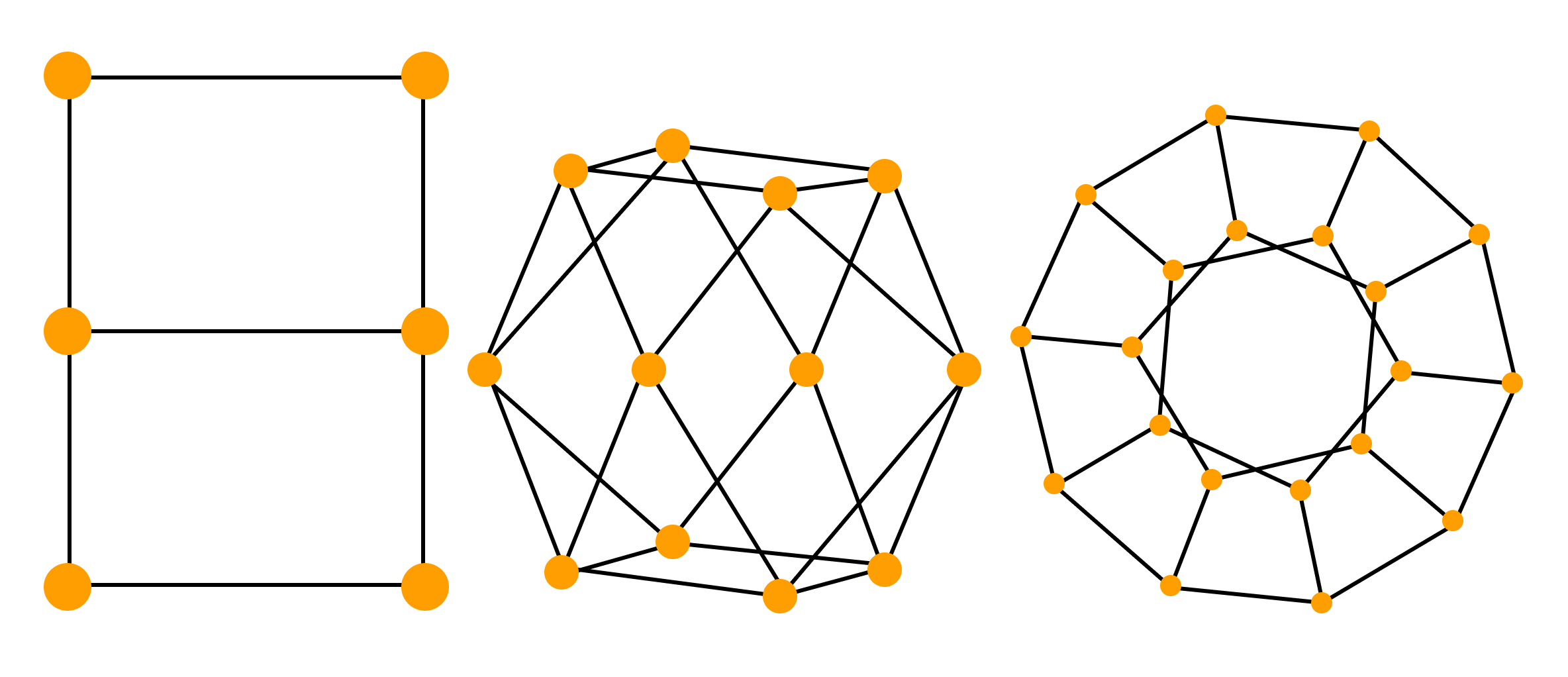
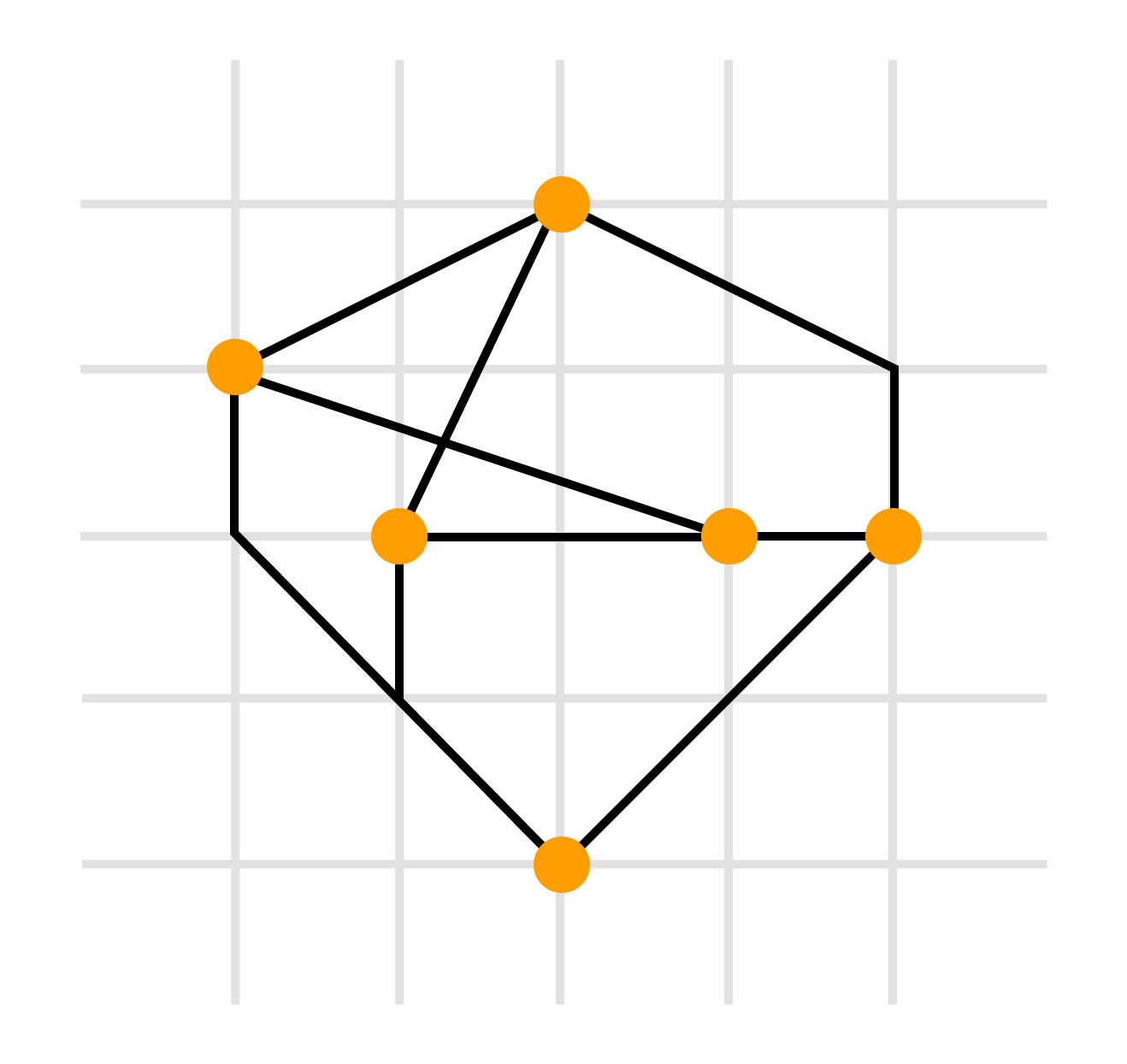
Другое замечание касается вида графа. Попробуйте проверить, что граф для одной и той же задачи можно нарисовать разными способами; и наоборот для разных задач можно нарисовать одинаковые по виду графы. Здесь важно лишь то, какие вершины соединены друг с другом, а какие – нет. Например, граф для задачи 1 можно нарисовать по-другому:
Такие одинаковые, но по-разному нарисованные графы, называются изоморфными.
Степени вершин и подсчет числа ребер графа
Запишем еще одно определение: Степенью вершины графа называется количество выходящих из нее ребер. В связи с этим, вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной.
С понятием степени вершины связана одна из основных теорем теории графов –теорема о честности числа нечетных вершин. Докажем ее мы немного позднее, а сначала для иллюстрации рассмотрим задачу.
Задача 3. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими ?
Решение: Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 5 проводов, т.е. степень каждой вершины нашего графа – 5. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т.к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза). Но тогда количество проводов получится разным 
Ответ. Соединить телефоны таким образом невозможно.
Теорема: Любой граф содержит четное число нечетных вершин.
Доказательство: Количество ребер графа равно половине суммы степеней его вершин. Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной. А это возможно только в том случае, если граф содержит четное число нечетных вершин.
Есть еще одно важное понятие, относящееся к графам – понятие связности.
Граф называется связным, если из любые две его вершины можно соединить путем, т.е. непрерывной последовательностью ребер. Существует целый ряд задач, решение которых основано на понятии связности графа.
Задача 4. В стране Семерка 15 городов, каждый из городов соединен дорогами не менее, чем с семью другими. Докажите, что из каждого города модно добраться в любой другой.
Доказательство: Рассмотрим два произвольных А и В города и допустим, что между ними нет пути. Каждый из них соединен дорогами не менее, чем с семью другими, причем нет такого города, который был бы соединен с обоими рассматриваемыми городами (в противном случае существовал бы путь из A в B). Нарисуем часть графа, соответствующую этим городам:
Теперь явно видно, что мы получили не менее различных 16 городов, что противоречит условию задачи. Значит утверждение доказано от противного.
Если принять во внимание предыдущее определение, то утверждение задачи можно переформулировать и по-другому: “Доказать, что граф дорог страны Семерка связен.”
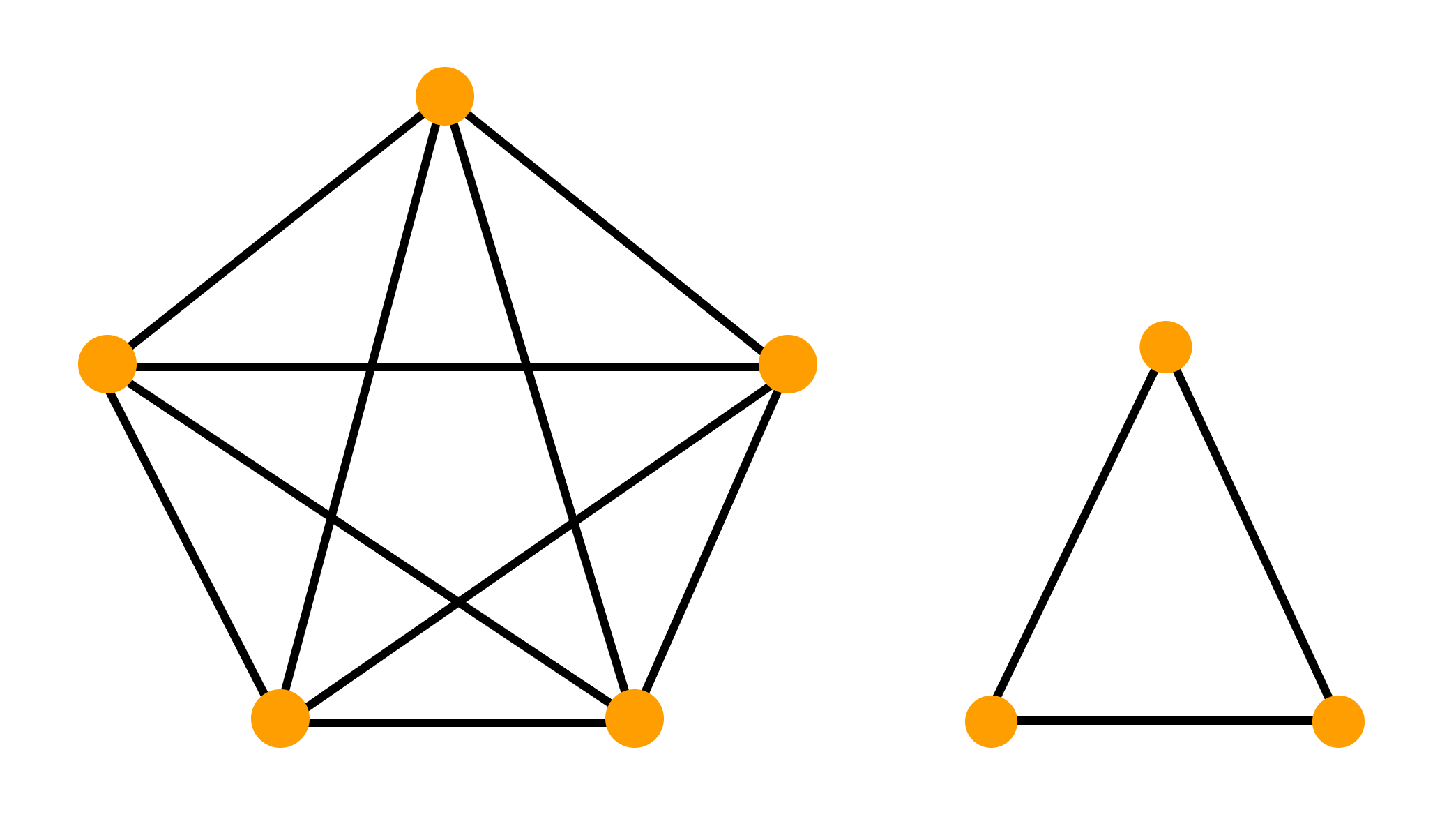
Теперь вы знаете, как выглядит связный граф. Несвязный граф имеет вид нескольких “кусков”, каждый из которых – либо отдельная вершина без ребер, либо связный граф. Пример несвязного графа вы видите на рисунке:
Каждый такой отдельный кусок называется компонентой связности графа. Каждая компонента связности представляет собой связный граф и для нее выполняются все утверждения, которые мы доказали для связных графов. Рассмотрим пример задачи, в которой используется компонента связности:
Задача 5. В Тридевятом царстве только один вид транспорта – ковер-самолет. Из столицы выходит 21 ковролиния, из города Дальний – одна, а из всех остальных городов, – по 20. Докажите, что из столицы можно долететь в город Дальний.
Доказательство: Понятно, что если нарисовать граф ковролиний Царства, то он может быть несвязным. Рассмотрим компоненту связности, которая включает в себя столицу Царства. Из столицы выходит 21 ковролиния, а из любых других городов, кроме города Дальний – по 20, поэтому, чтобы выполнялся закон о четном числе нечетных вершин необходимо, чтобы и город Дальний входил в эту же самую компоненту связности. А так как компонента связности – связный граф, то из столицы существует путь по ковролиниям до города Дальний, что и требовалось доказать.
Вы наверняка сталкивались с задачами, в которых требуется нарисовать какую-либо фигуру не отрывая карандаш от бумаги и проводя каждую линию только один раз. Оказывается, что такая задача не всегда разрешима, т.е. существуют фигуры, которые указанным способом нарисовать нельзя. Вопрос разрешимости таких задач также входит в теорию графов. Впервые его исследовал в 1736 году великий немецкий математик Леонард Эйлер, решая задачу о Кенигсбергских мостах. Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.
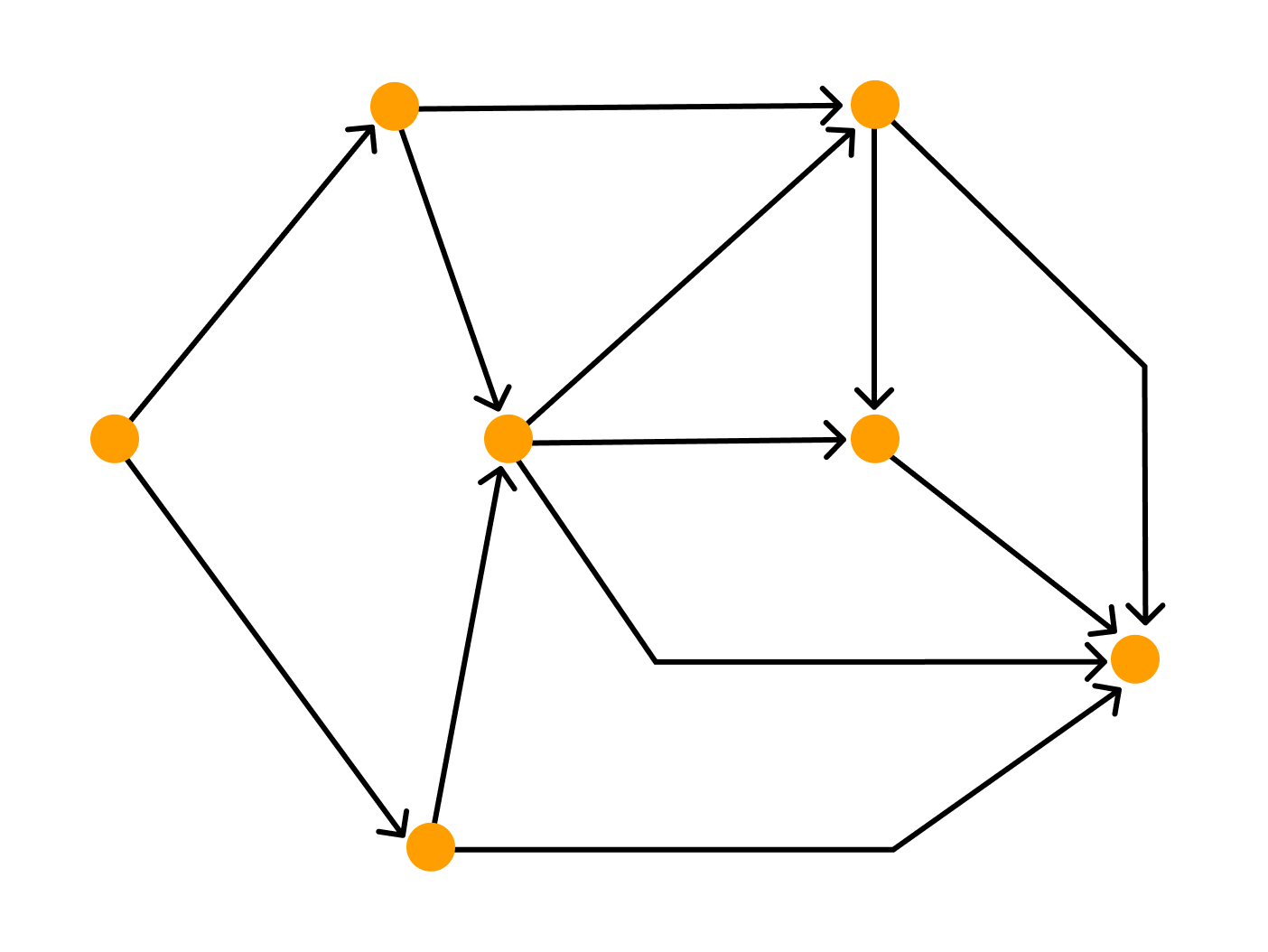
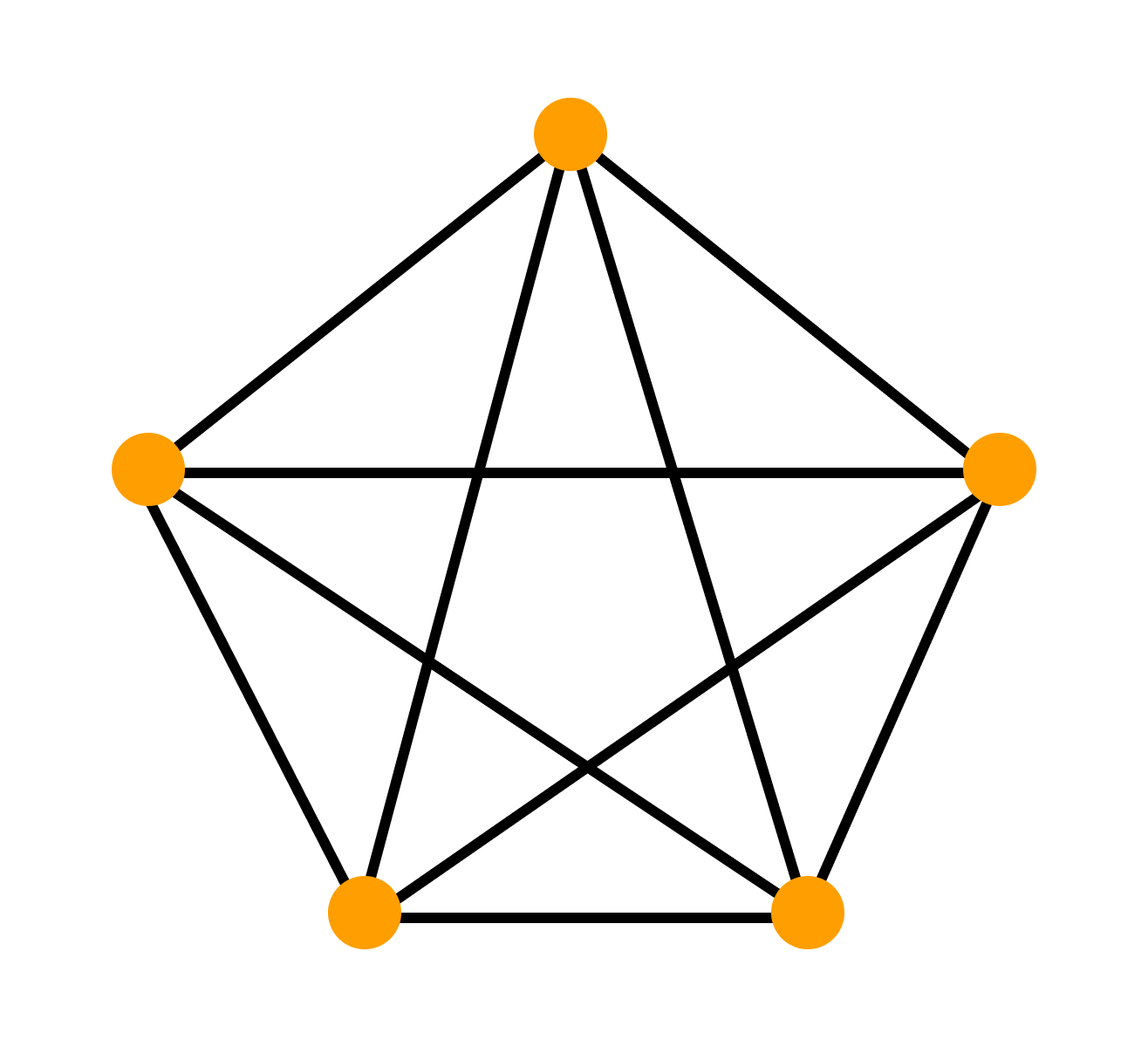
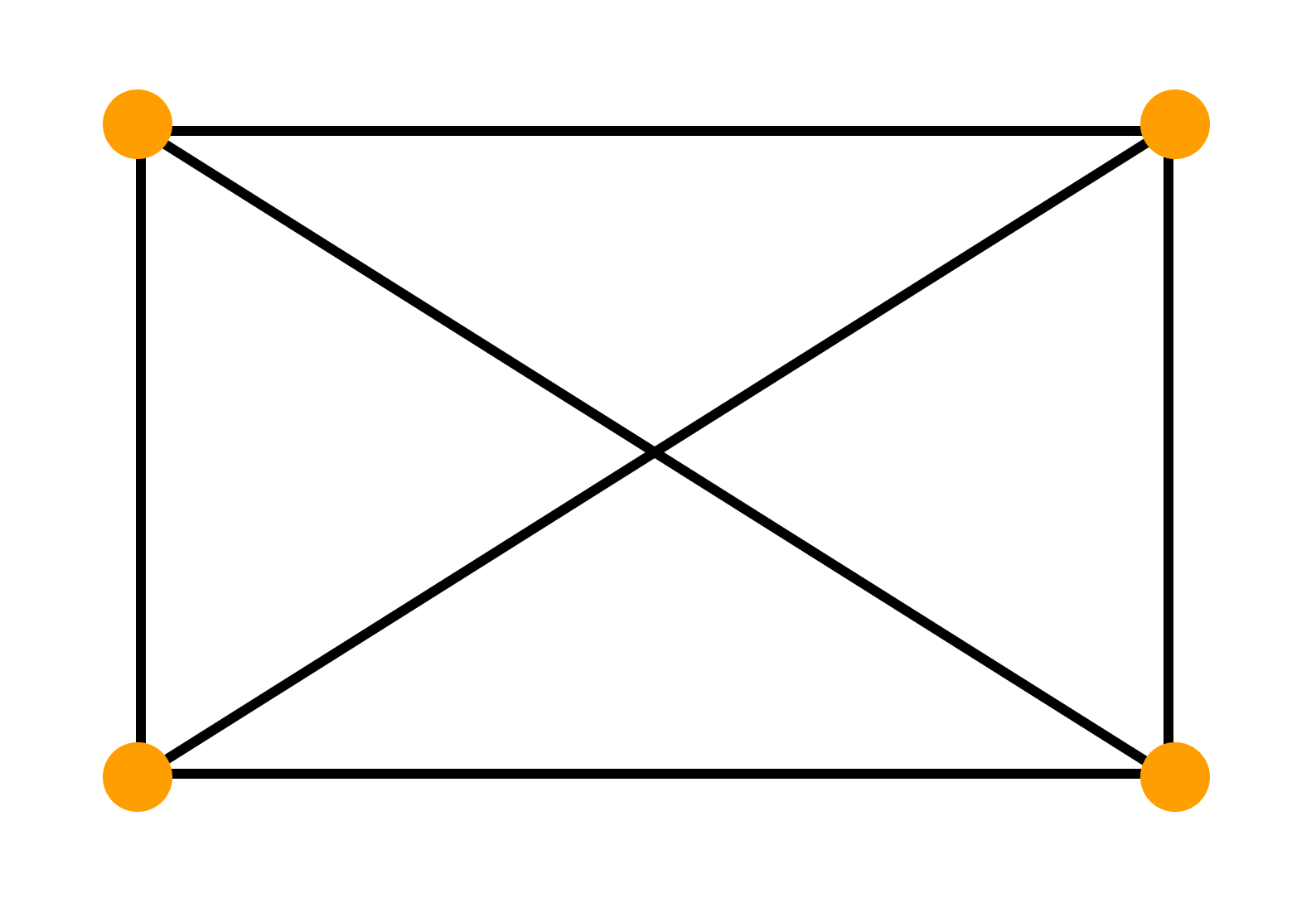
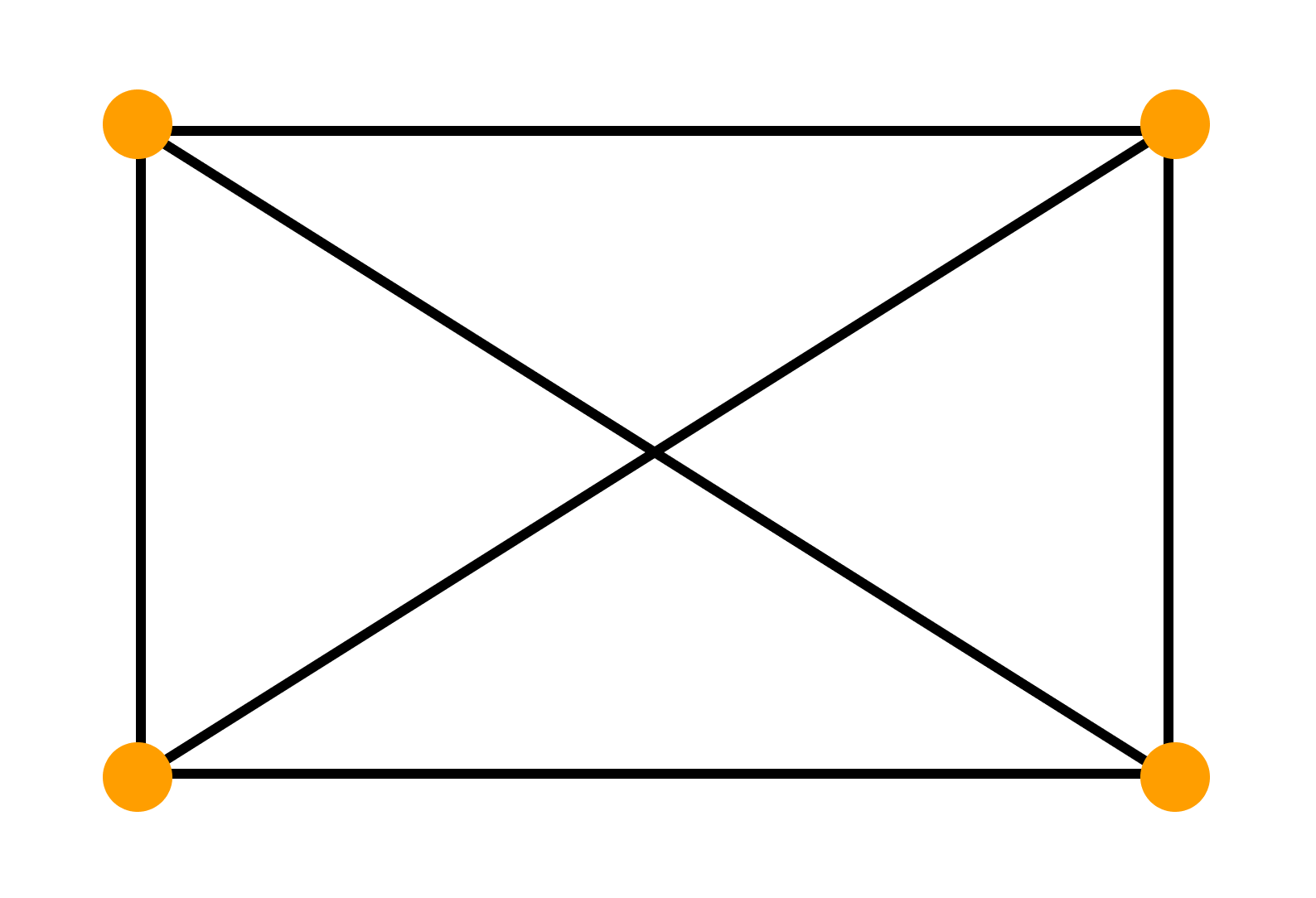
Задача 6. Можно ли нарисовать изображенный на рисунке граф не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз ?
Решение. Если мы будем рисовать граф так, как сказано в условии, то в каждую вершину, кроме начальной и конечной, мы войдем столько же раз, сколько выйдем из нее. То есть все вершины графа, кроме двух должны быть четными. В нашем же графе имеется три нечетные вершины, поэтому его нельзя нарисовать указанным в условии способом.
Сейчас мы доказали теорему об Эйлеровых графах:
Теорема: Эйлеров граф должен иметь не более двух нечетных вершин.
И в заключение – задача о Кенигсбергских мостах.
Задача 7. На рисунке изображена схема мостов города Кенигсберга.
Можно ли совершить прогулку так, чтобы пройти по каждому мосту ровно 1 раз?
3. Задачи к теме “Графы”
Понятие графа.
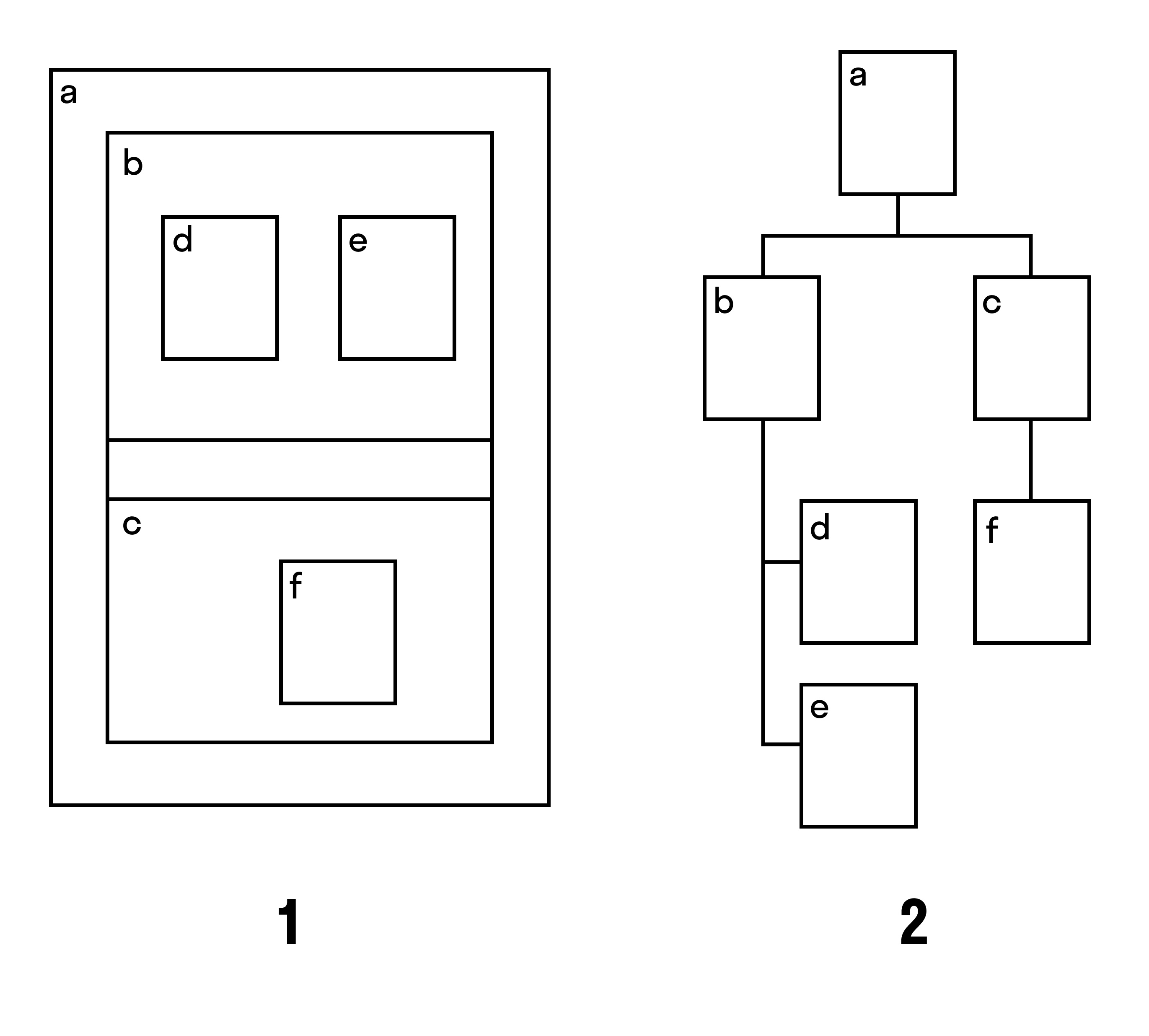
1. На квадратной доске 3×3 расставлены 4 коня так, как показано на рис.1. Можно ли сделав несколько ходов конями, переставить их в положение, показанное на рис.2?
 |
Рис. 1

Решение. Занумеруем клетки доски, как показано на рисунке:
Каждой клетке поставим в соответствие точку на плоскости и, если из одной клетки можно попасть в другую ходом шахматного коня, то соответствующие точки соединим линией. Исходная и требуемая расстановки коней показаны на рисунках:
 |  |
При любой последовательности ходов конями порядок их следования, очевидно, измениться не может. Поэтому переставить коней требуемым образом невозможно.
2. В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, образованное названиями городов, делится на 3. Можно ли долететь по воздуху из города 1 в город 9 ?
Решение. Поставив в соответствие каждому городу точку и соединив точки линией, если сумма цифр делится на 3, получим граф, в котором цифры 3, 5, 9 связаны между собой, но не связаны с остальными. Значит долететь из города 1 в город 9 нельзя.
Степени вершин и подсчет числа ребер.
3. В государстве 100 городов к из каждого города выходит 4 дороги. Сколько всего дорог в государстве.
Решение. Подсчитаем общее количество выходящих городов дорог – 100 . 4 = 400. Однако при таком подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 200.
4. В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей ?
Ответ. Нет (теорема о четности числа нечетных вершин).
5. У короля 19 вассалов. Может ли оказаться так, что у каждого вассала 1, 5 или 9 соседей ?
Ответ. Нет, не может.
6. Может ли в государстве, в котором из каждого города выходит ровно 3 дороги, быть ровно 100 дорог?
Решение. Подсчитаем число городов. Число дорог равно числу городов х, умноженному на 3 (число выходящих из каждого города дорог) и разделенному на 2 (см. задачу 3). Тогда 100 = Зх/2 => Зх=200, чего не может быть при натуральном х. Значит 100 дорог в таком государстве быть не может.
7. Докажите, что число людей, живших когда-либо на Земле и сделавших нечетное число рукопожатий, четно.
Доказательство непосредственно следует из теоремы о четности числа нечетных вершин графа.
Связность.
8. В стране из каждого города выходит 100 дорог и из каждого города можно добраться до любого другого. Одну дорогу закрыли на ремонт. Докажите, что и теперь из любого города можно добраться до любого другого.
Доказательство. Рассмотрим компоненту связности, в которую входит один из городов, дорогу между которыми закрыли. По теореме о четности числа нечетных вершин в нее входит и второй город. А значит по-прежнему можно найти маршрут и добраться из одного из этих городов в другой.
Графы Эйлера.
9. Имеется группа островов, соединенных мостами так, что от каждого острова можно добраться до любого другого. Турист обошел все острова, пройдя по каждому мосту розно 1 раз. На острове Троекратном он побывал трижды. Сколько мостов ведет с Троекратного, если турист
а) не с него начал и не на нем закончил?
б) с него начал, но не на нем закончил?
в) с него начал и на нем закончил?
10. На рисунке изображен парк, разделенный на несколько частей заборами. Можно ли прогуляться по парку и его окрестностям так, чтобы перелезть через каждый забор розно 1 раз?
Источник
Теория графов. Основные понятия и виды графов
О чем эта статья:
Теория графов
В переводе с греческого граф — «пишу», «описываю». В современном мире граф описывает отношения. И наоборот: любое отношение можно описать в виде графа.
Теория графов — обширный раздел дискретной математики, в котором системно изучают свойства графов.
Теория графов широко применяется в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических цепей, коммуникации, психологии, социологии, лингвистике и в других областях.
Для чего строят графы: чтобы отобразить отношения на множествах. По сути, графы помогают визуально представить всяческие сложные взаимодействия: аэропорты и рейсы между ними, разные отделы в компании, молекулы в веществе.
Давайте на примере.
Пусть множество A =
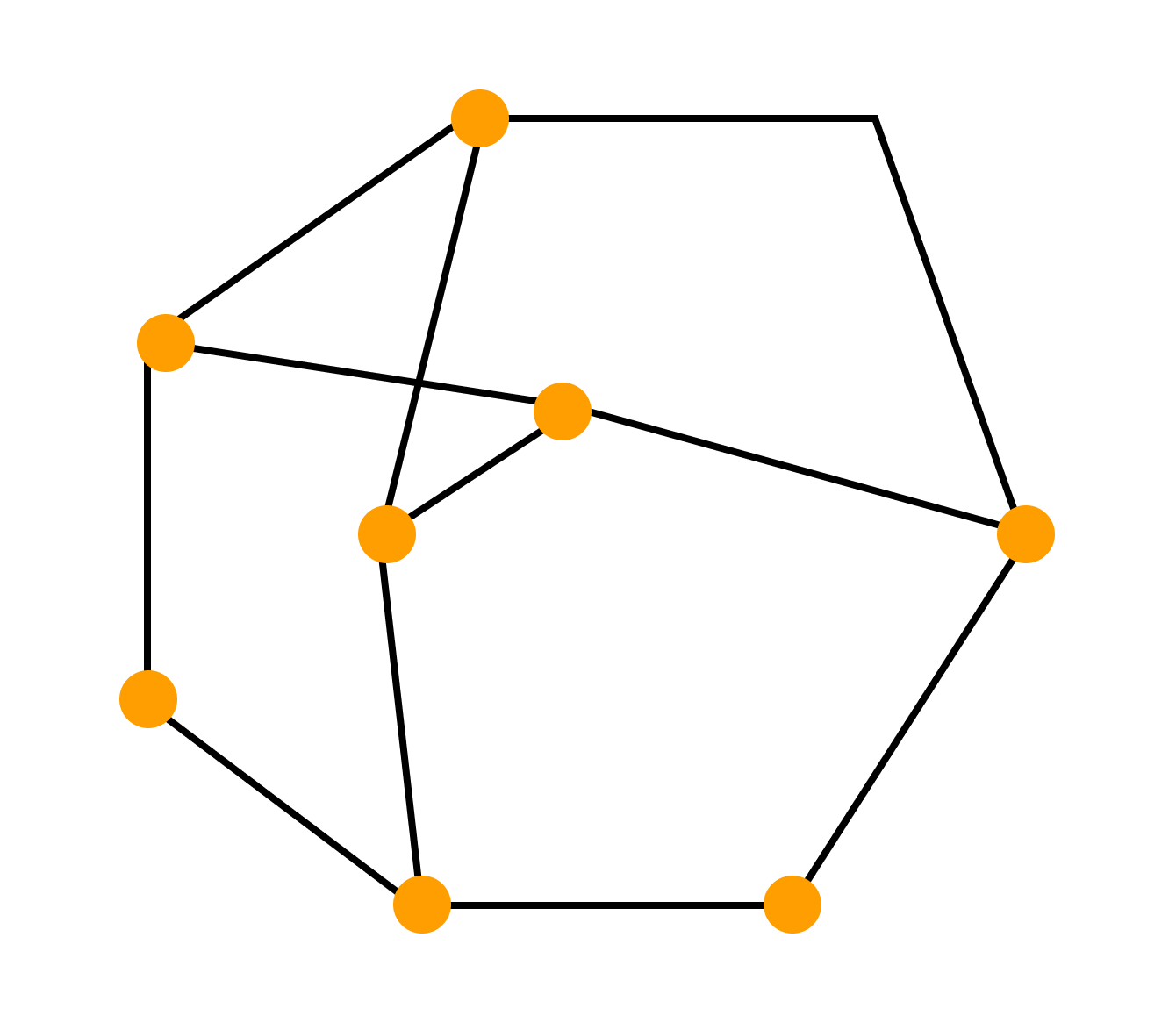
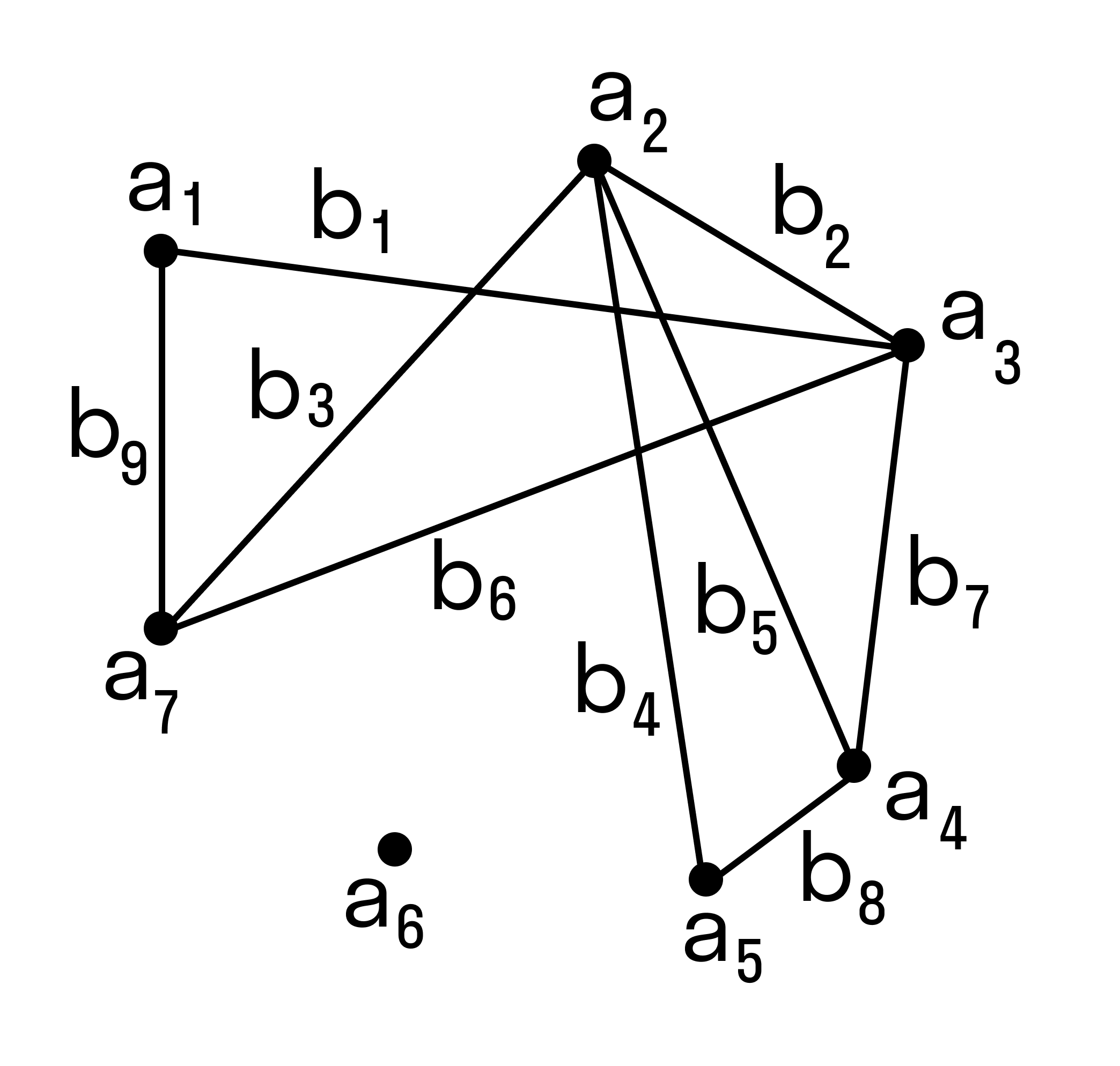
На множестве A зададим отношение знакомства между людьми из этого множества. Строим граф из точек и связок. Связки будут связывать пары людей, знакомых между собой.
Число знакомых у одних людей может отличаться от числа знакомых у других людей, некоторые могут вовсе не быть знакомы (такие элементы будут точками, не соединёнными ни с какой другой). Так получился граф:
В данном случае точки — это вершины графа, а связки — рёбра графа.
Теория графов не учитывает конкретную природу множеств A и B. Существует большое количество разных задач, при решении которых можно временно забыть о содержании множеств и их элементов. Эта специфика не отражается на ходе решения задачи.
Например, вопрос в задаче стоит так: можно ли из точки A добраться до точки E, если двигаться только по соединяющим точки линиям. Когда задача решена, мы получаем решение, верное для любого содержания, которое можно смоделировать в виде графа.
Не удивительно, что теория графов — один из самых востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может обсудить с человеком вопросы отношений, географии или музыки, решения различных задач.
Графом называется система объектов произвольной природы (вершин) и связок (ребер), соединяющих некоторые пары этих объектов.
Пусть V — (непустое) множество вершин, элементы v ∈ V — вершины. Граф G = G(V) с множеством вершин V есть некоторое семейство пар вида: e = (a, b), где a, b ∈ V, указывающих, какие вершины остаются соединёнными. Каждая пара e = (a, b) — ребро графа. Множество U — множество ребер e графа. Вершины a и b — концевые точки ребра e.
Широкое применение теории графов в компьютерных науках и информационных технологиях можно объяснить понятием графа как структуры данных. В компьютерных науках и информационных технологиях граф можно описать, как нелинейную структуру данных.
Линейные структуры данных особенны тем, что связывают элементы отношениями по типу «простого соседства». Линейными структурами данных можно назвать массивы, таблицы, списки, очереди, стеки, строки. В нелинейных структурах данных элементы располагаются на различных уровнях иерархии и подразделяются на три вида: исходные, порожденные и подобные.
Основные понятия теории графов
Граф — это геометрическая фигура, которая состоит из точек и линий, которые их соединяют. Точки называют вершинами графа, а линии — ребрами.
- Два ребра называются смежными, если у них есть общая вершина.
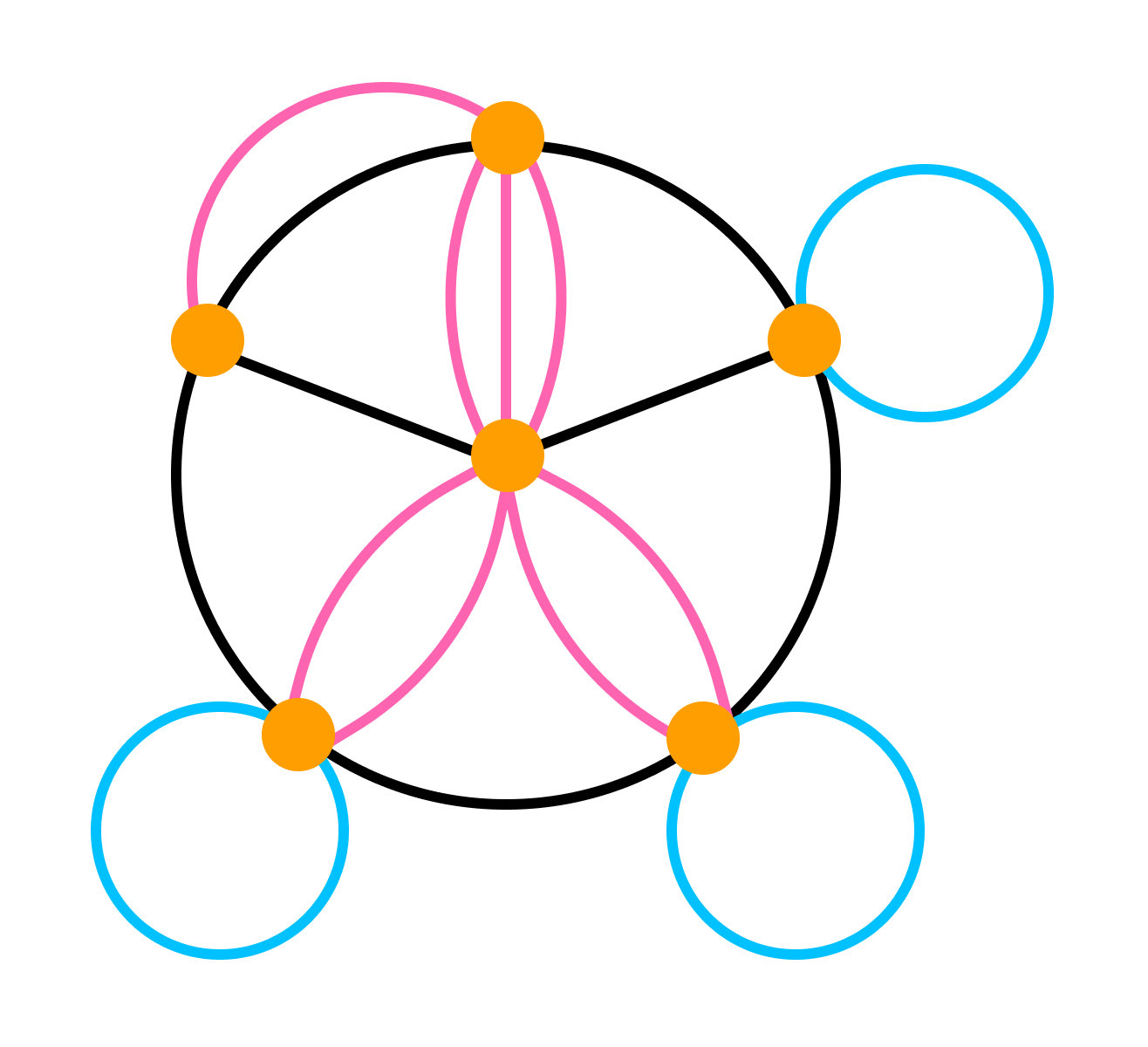
- Два ребра называются кратными, если они соединяют одну и ту же пару вершин.
- Ребро называется петлей, если его концы совпадают.
- Степенью вершины называют количество ребер, для которых она является концевой (при этом петли считают дважды).
- Вершина называется изолированной, если она не является концом ни для одного ребра.
- Вершина называется висячей, если из неё выходит ровно одно ребро.
- Граф без кратных ребер и петель называется обыкновенным.