- Понятие графа. Способы задания графа. Основные операции над графами. Основные типы графов.
- Теория графов. Основные понятия и виды графов
- Теория графов
- Основные понятия теории графов
- Путь и цепь в графе
- Визуализация графовых моделей
- Виды графов
- Ориентированные и неориентированные графы
- Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы
- Двудольный граф
- Эйлеров граф
- Регулярный граф
- Гамильтонов граф
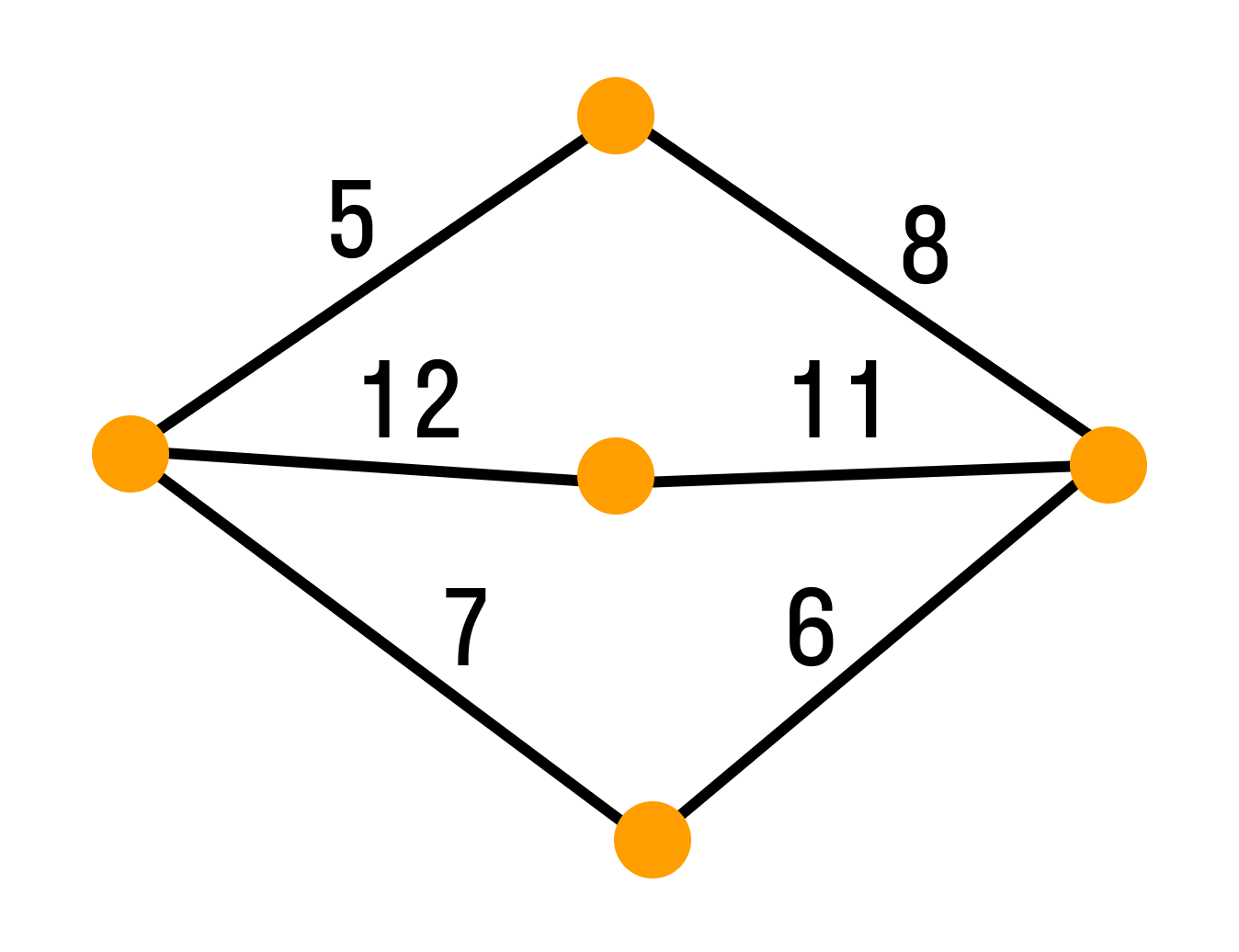
- Взвешенный граф
- Графы-деревья
- Определение дерева
- Теоремы дерева и их доказательства
- Теория графов и современные прикладные задачи
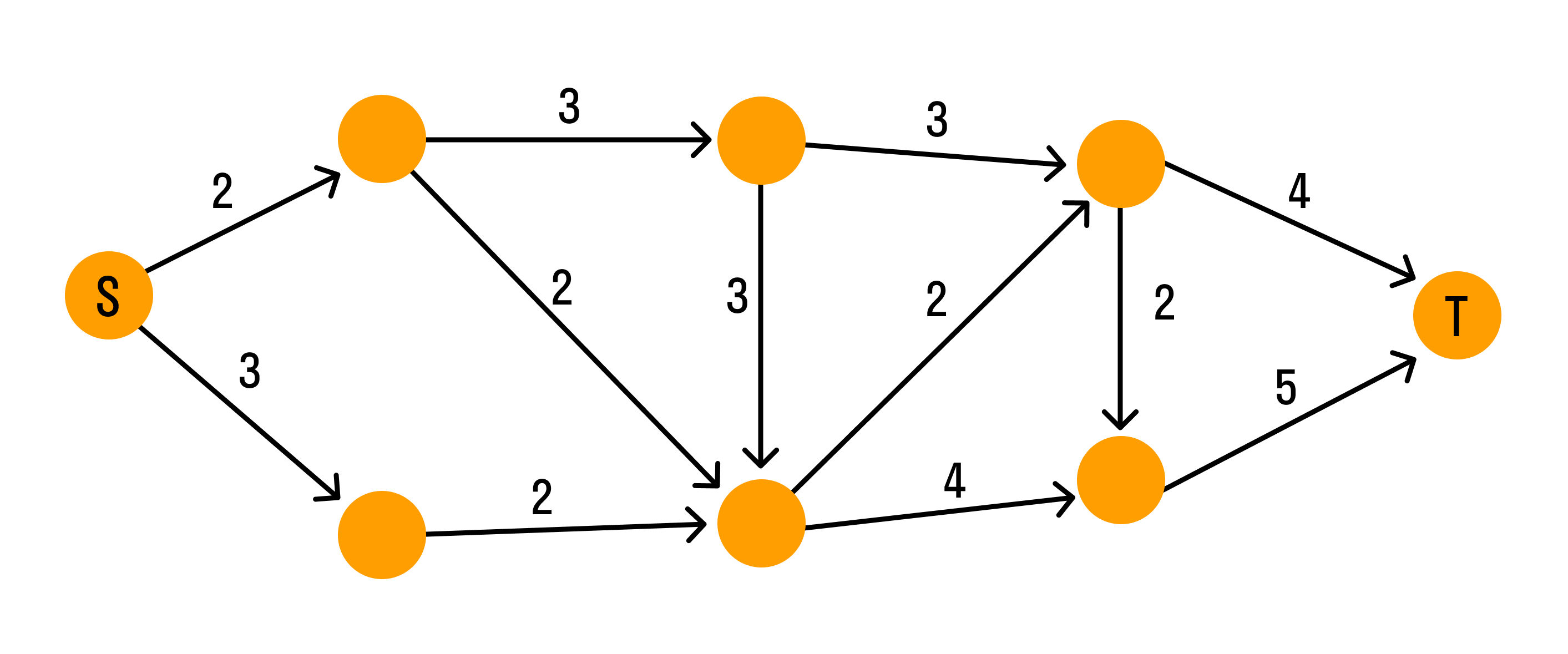
- Графы и задача о потоках
- Графы и сетевое планирование
Понятие графа. Способы задания графа. Основные операции над графами. Основные типы графов.



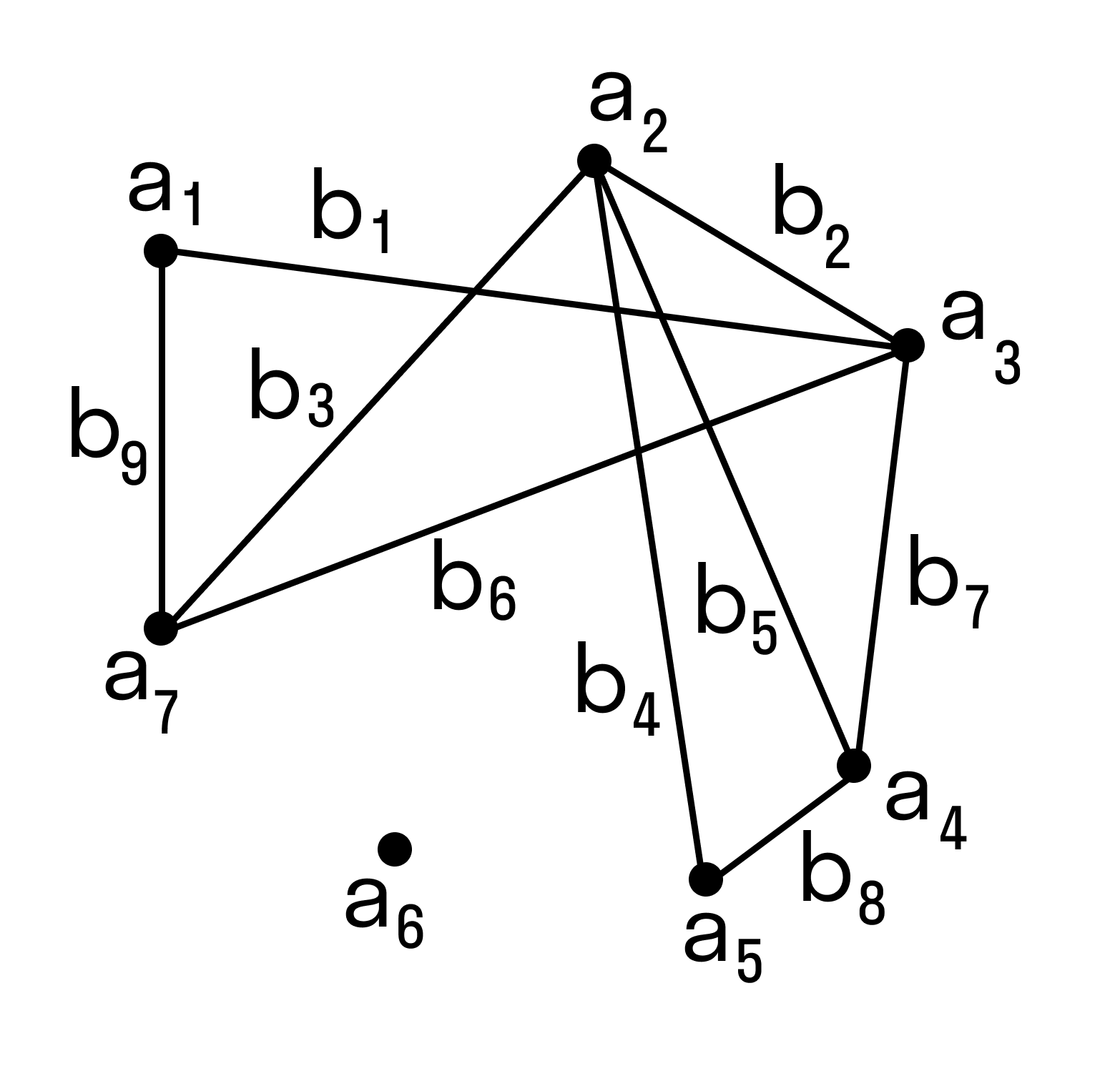
Графом будем называть совокупность 2х конечных множеств вершин Х и ребер (или дуг) U
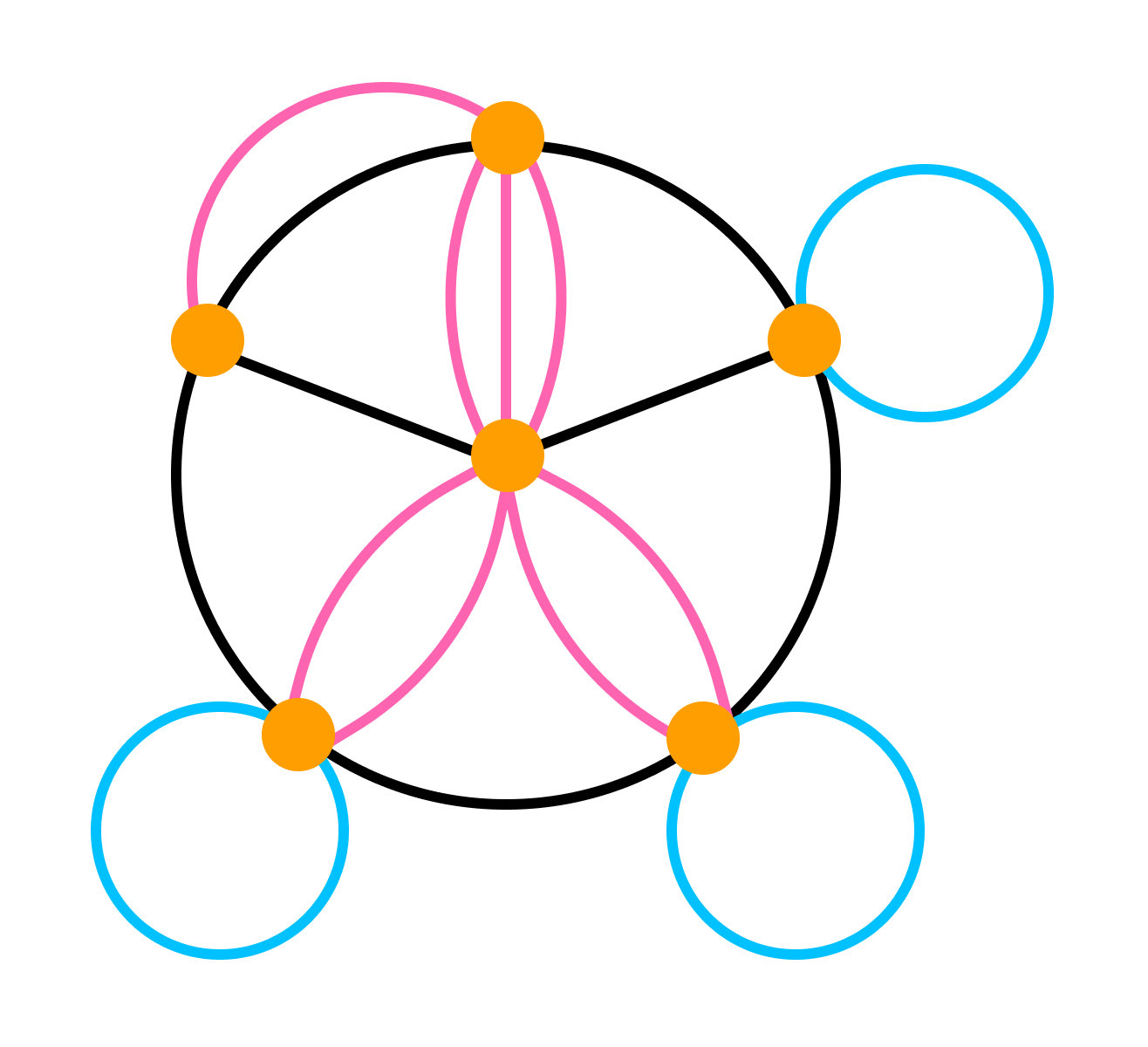
Если порядок соединения вершин (хi xj) является не существенным, то граф называется не ориентированным (неорграф), а пара (хi xj) — ребра этого графа. Если порядок соединения вершин (хi xj) является существенным, то граф называется ориентированным (орграф), а пара (хi xj) — дуги этого графа.. Граф, в котором имеются и дуги и ребра называется смешанным .Любое ребро не орграфа можно заменить парой дуг. Пара вершин графа (хi xj) может соединяться 2 я и более ребрами (дугами одного направления). Такие ребра (дуги) называются кратными. Количество одинаковых ребер (дуг) называется кратностью соответствующего ребра (дуги). Две вершины графа называются смежными, если существует соединяющее их ребро (дуга). 2 ребра называются смежными, если они имеют общею вершину. Петлей называются ребра, с совпадающей начальной и конечной вершиной. Граф с петлями и кратными дугами называется псевдограф, граф без петель и с кратными дугами называется мультиграф.
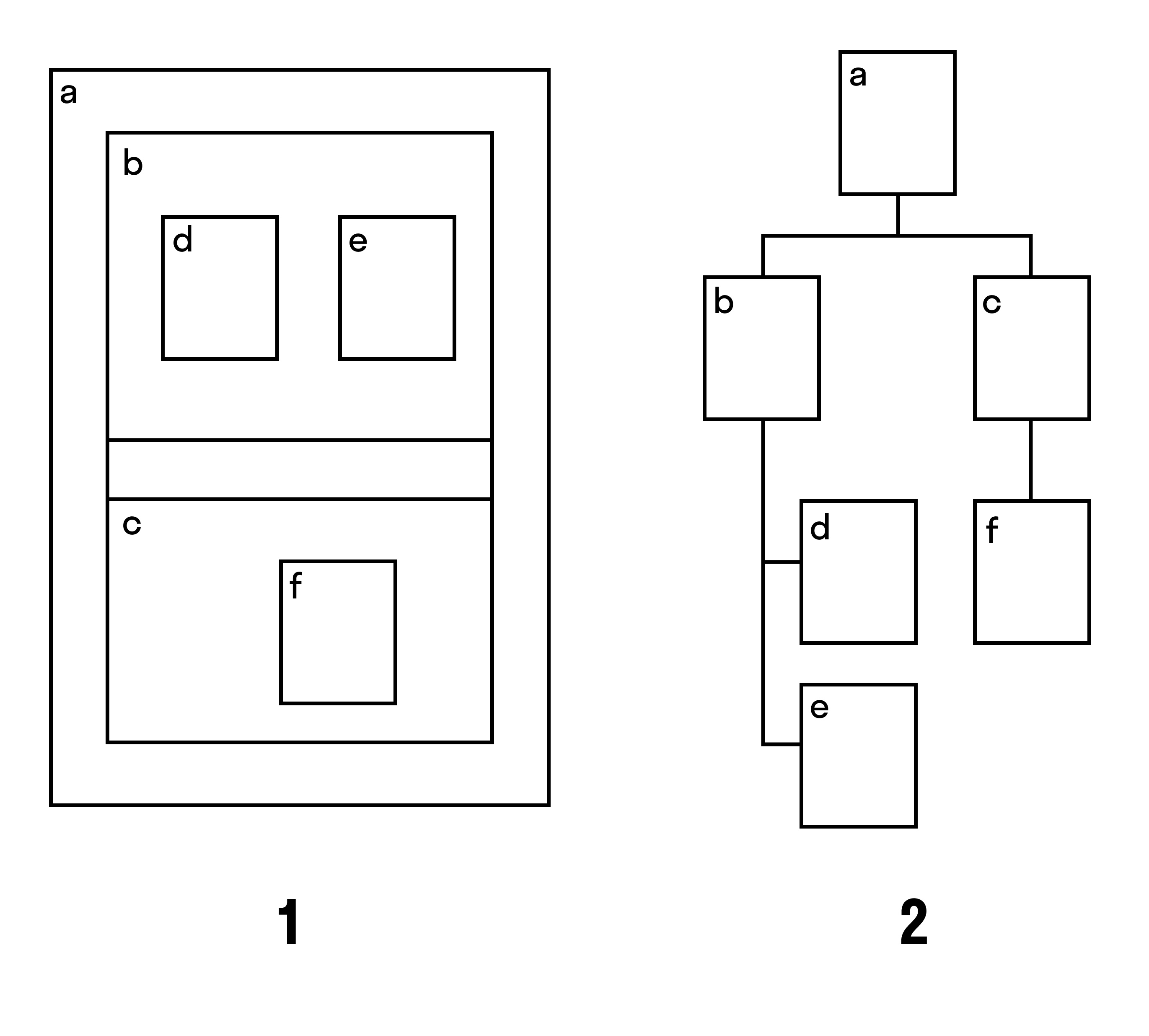
Подграфом графа G (х,u) называется граф G1(х1,u1), в котором множество x1 является подмножеством X, u1 является подмножеством u. Оставным подграфом графа G называется граф, содержащий все вершины графа G. Порожденный подграф состоит из подмножества вершин Xs множества вершин исходного графа и всех таких дуг графа G, у которого конечные и начальные вершины принадлежат подмножеству Xs .
Число дуг, исходящих из вершины xi ориентированного графа называется полустепенью исхода, число дуг, входящих в вершину ориентированного графа – полустепенью захода. В неор. Графах число ребер инцидентных вершине называется степенью вершины хi.
Вершина, имеющая степень 0 — изолированной., а имеющая степень 1 — висячей.
Маршрут —в не орграфе: последовательность ребер, в которой начало каждого последующего ребра совпадает с концом предыдущего. В орграфе: последовательность дуг, в которой начало каждой последующей дуги совпадает с концом предыдущей. Цепь —незамкнутый маршрут, в котором все ребра различны. Цепь, в которой все вершины различны, называется простой цепью. Путь — ориентированный маршрут, в котором все дуги различны. Замкнутый путь —контур. Цикл—замкнутая цепь. Замкнутая про стая цепь -простой цикл. Способы задания графа:
— геометрический (рисунок) – матричный. Различают также:
— матицу смежности (размерность пхп, щ = 1, если вершиныХ1И Xj смежны)
— матрицу инцидентности (размерность nxm, bjj = 1, если вершинахi инцидентна ребру Uj [для неорграфа] или b= 1, если вершина xi начальная вершина дуги uij bij = -1, если вершина xi., конечная вершина дуги и uij [для орграфа])
Основные операции над графами:
— удаление вершины (при этом удаляются все инцидентные ребра) — удаление ребра (при этом его конечные вершины не удаляются)
— добавление ре бра (обратно удалению) — слияние вершин – все ребра становятся инцидентны одной вершине
— стягивание ребра (удаление ребра и слияние его вершин) — подразбиение ребра (из графа удаляется (хi xj) и добавляется 2 новых ребра:(хi х0 и(х0 xj), где х0 — новая вершина)
Основные типы графов:
— орграф и неорграф
— граф с петлями и кратными ребрами называется псевдографом. Граф с кратными ребрами и без петель — мульти граф. Граф без петель и ребер- простой.
— граф называется взвешенным, если его ребрам (х^ xj) ставится в соответствие веса. Граф называется связным, если любые 2 вершины соединены маршрутом.
— граф называется ациклическим, если он не содержит циклов.
— орграф называется симметрическим, если любые 2 смежные вершины имеют пару противоположно направленных дуг. Неорграф -симметрический..
— граф называется регулярным степени к или однородным , если степени всех его вершин одинаковы и равны к.Число ребер при этом m=0.5*n*k.
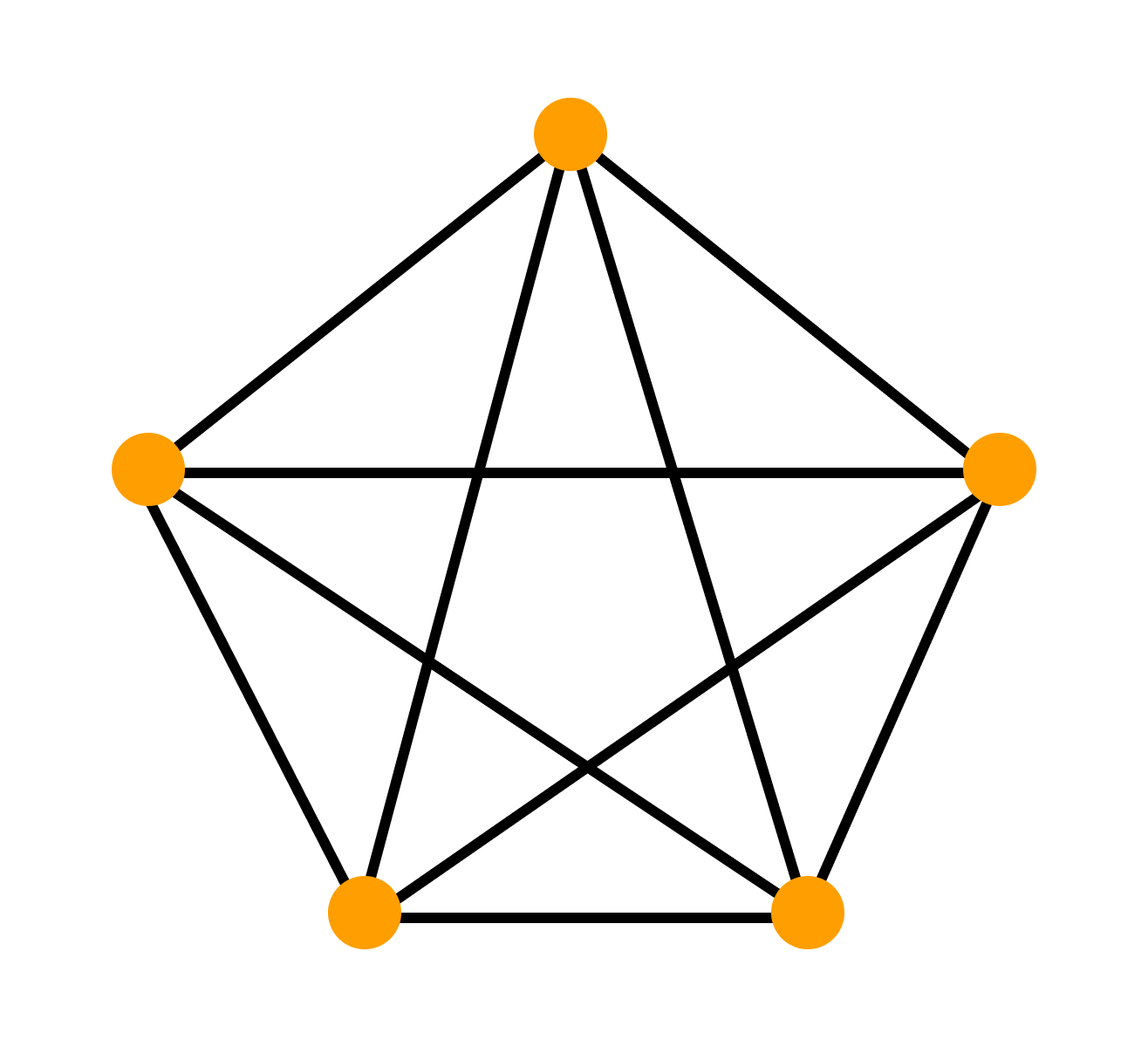
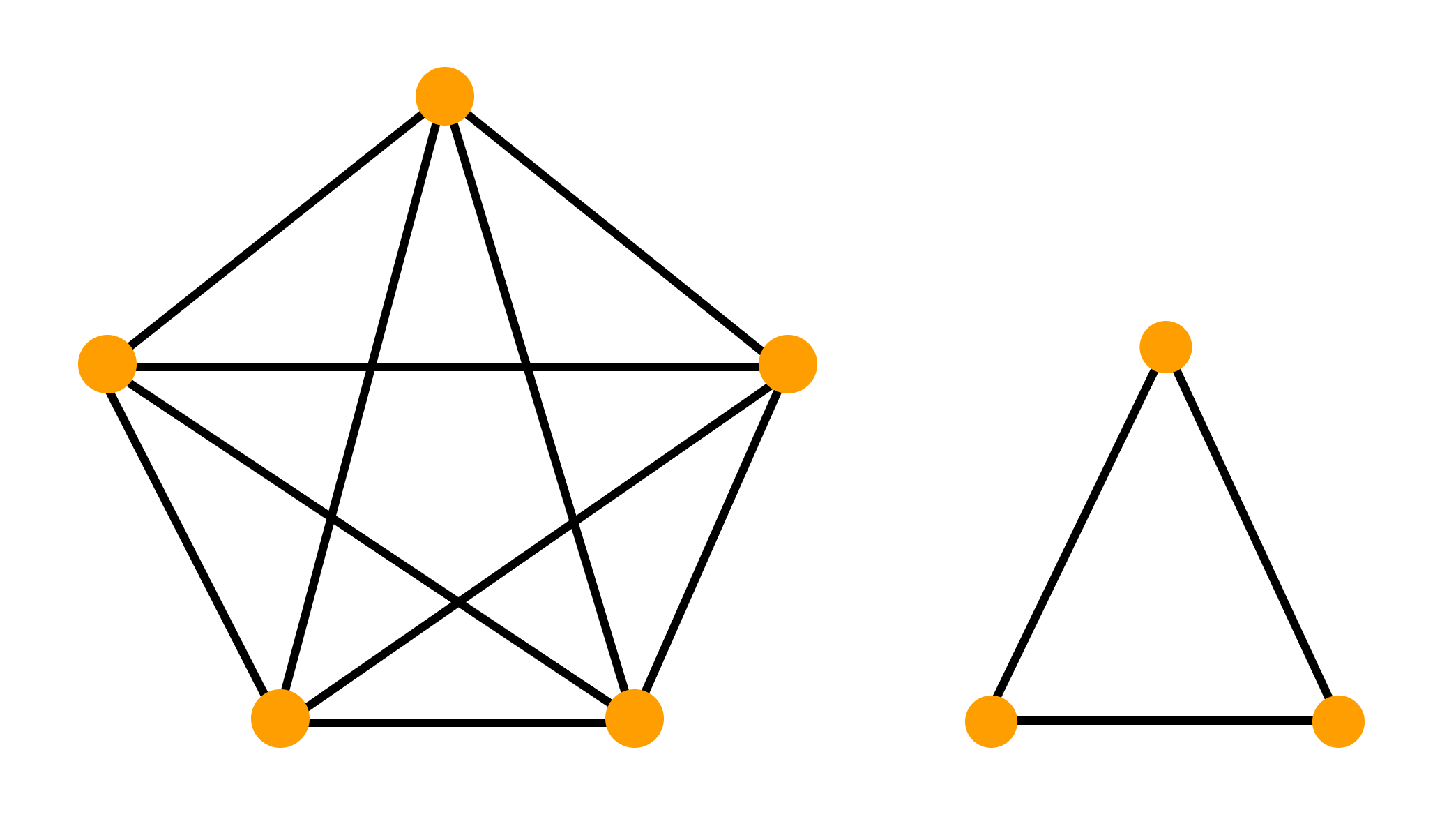
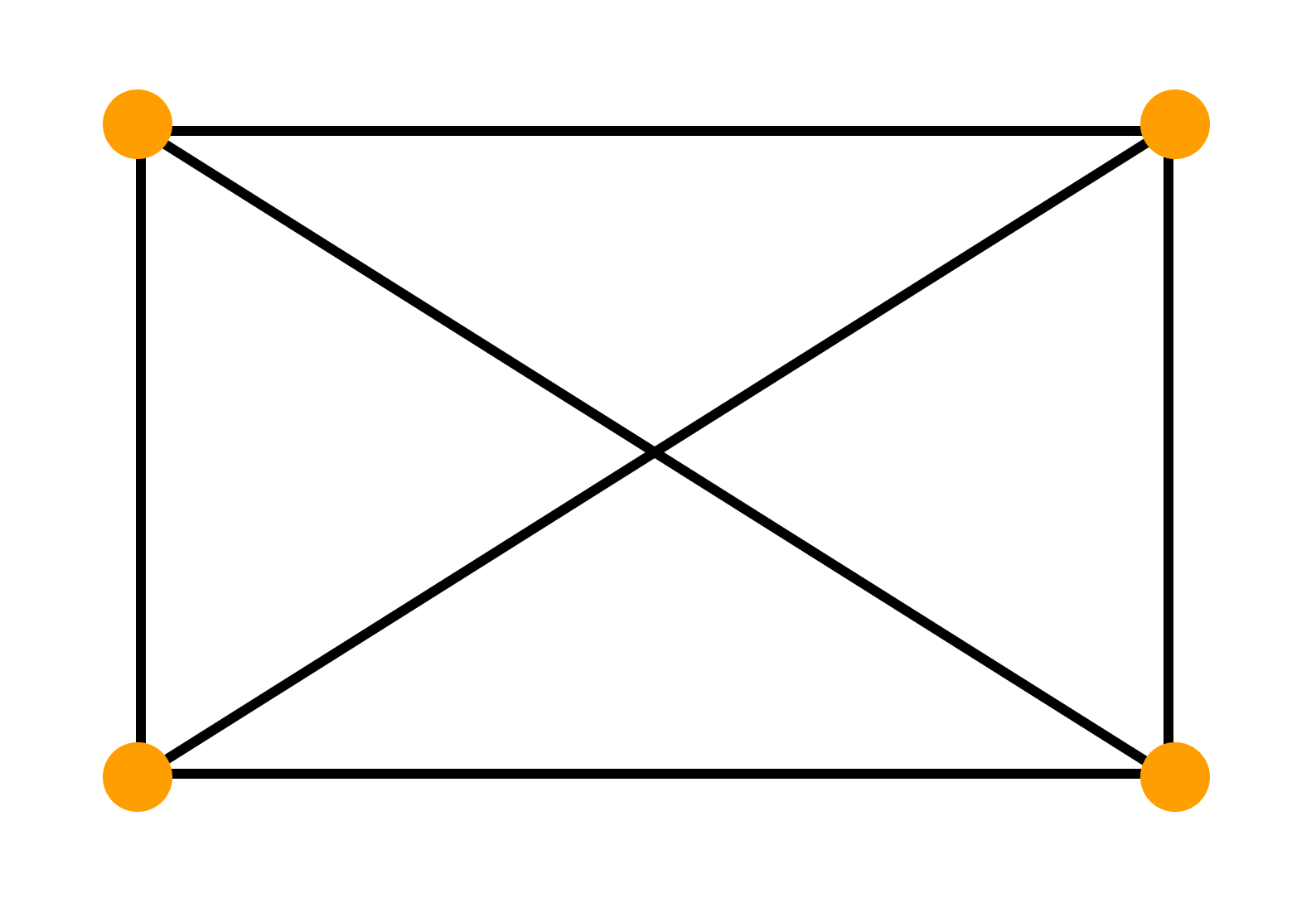
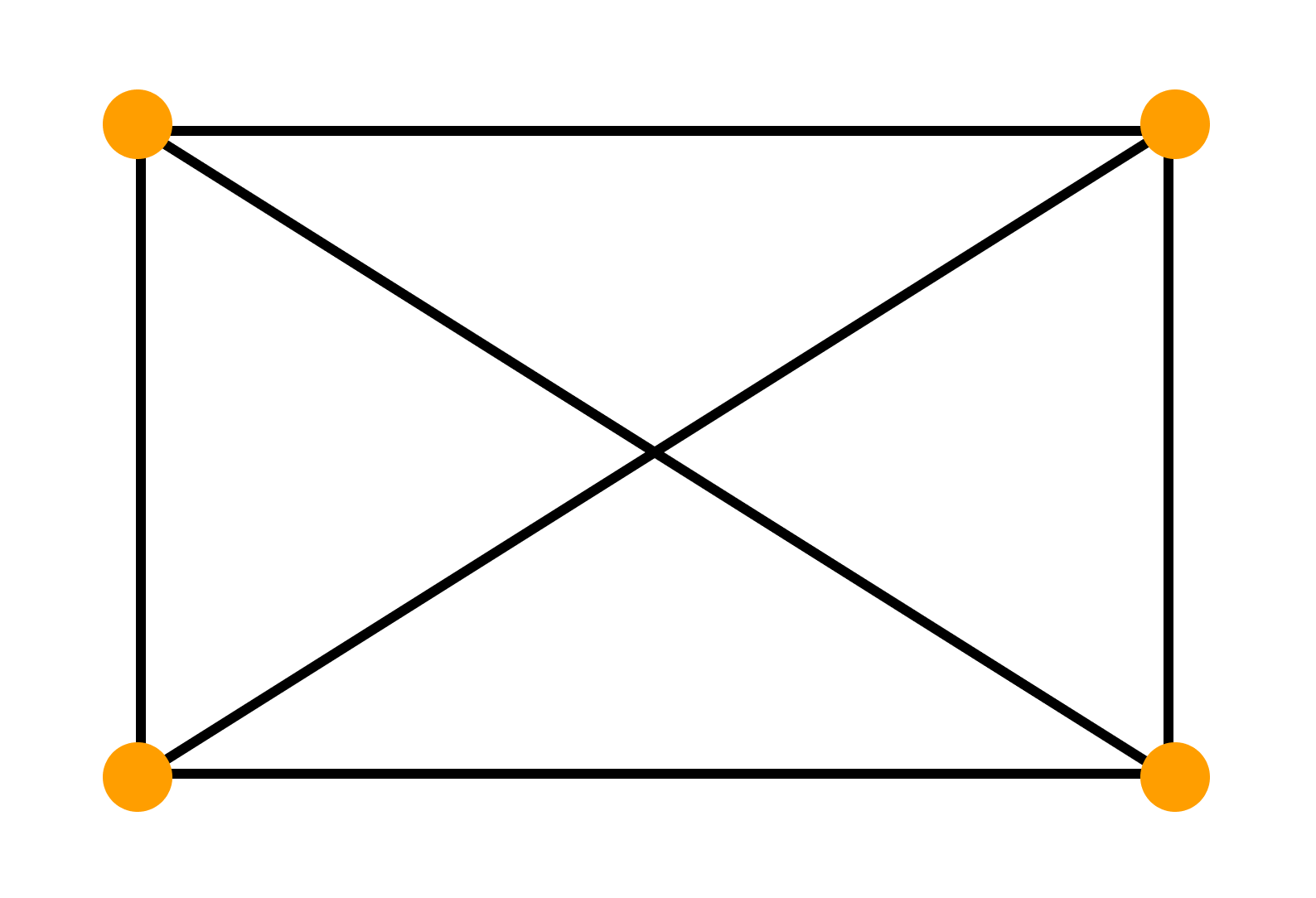
— граф называется полным, если все его вершины смежные. К» —полный граф, содержащий п вершин.
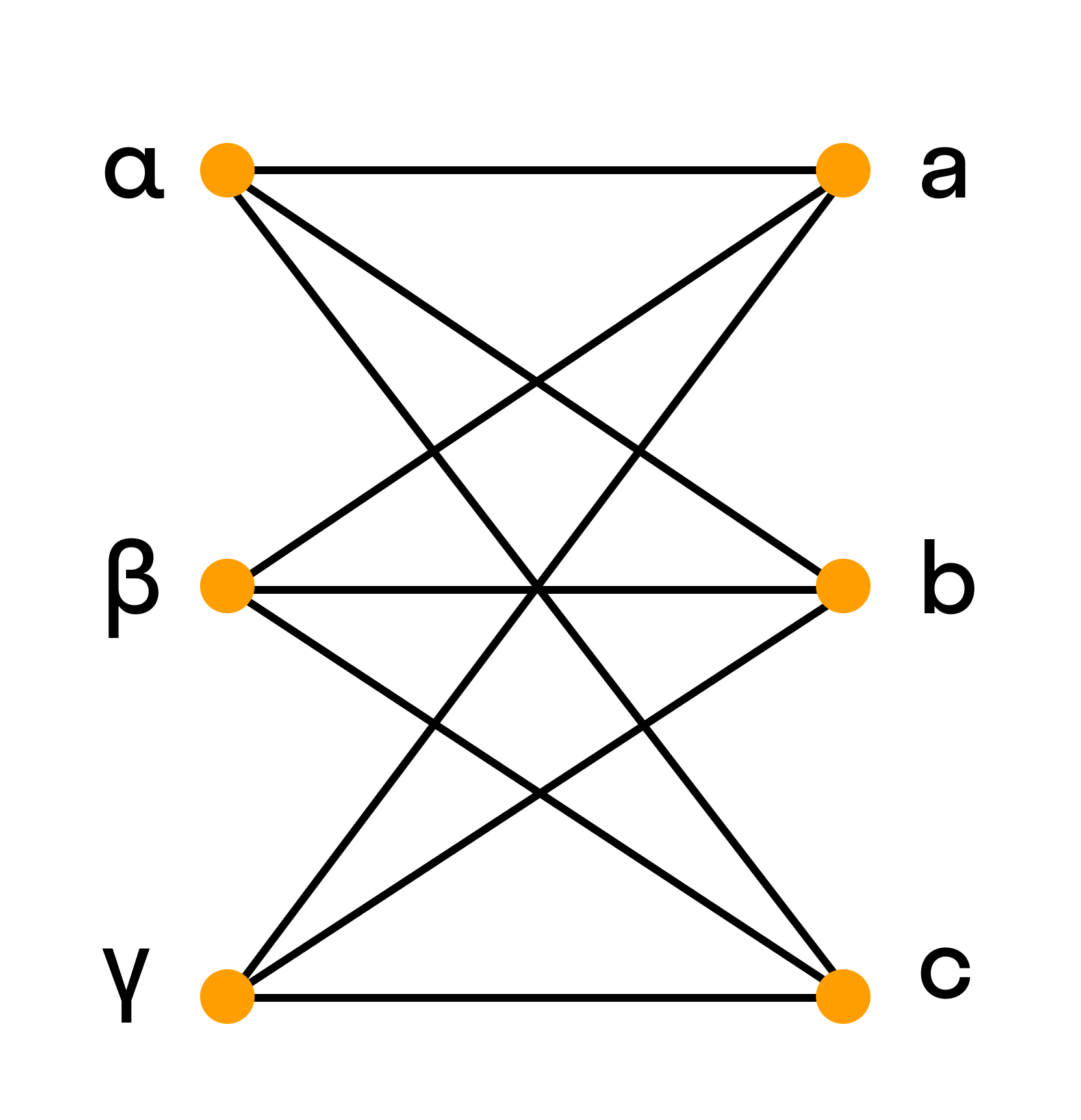
— граф (X, U) называется двудольным, если множество его вершин X можно разделить на 2 подмножества Х1 Х2 таким образом, что каждое ребро графа имеет 1 конечную вершину в множестве X1, а другую —в Х2. Множества X1, Х2 — доли. Если любые 2 вершины графа из разных долей смежные, граф называется полным двудольным графом.

— граф называется эйлеровым, если он содержит эйлеров цикл —цикл, проходящий через каждое ребро графа 1 раз.
— граф называется гамипьтоновым, если он содержит гамипьтонов цикл — цикл, проходящий через каждую вершину 1 раз
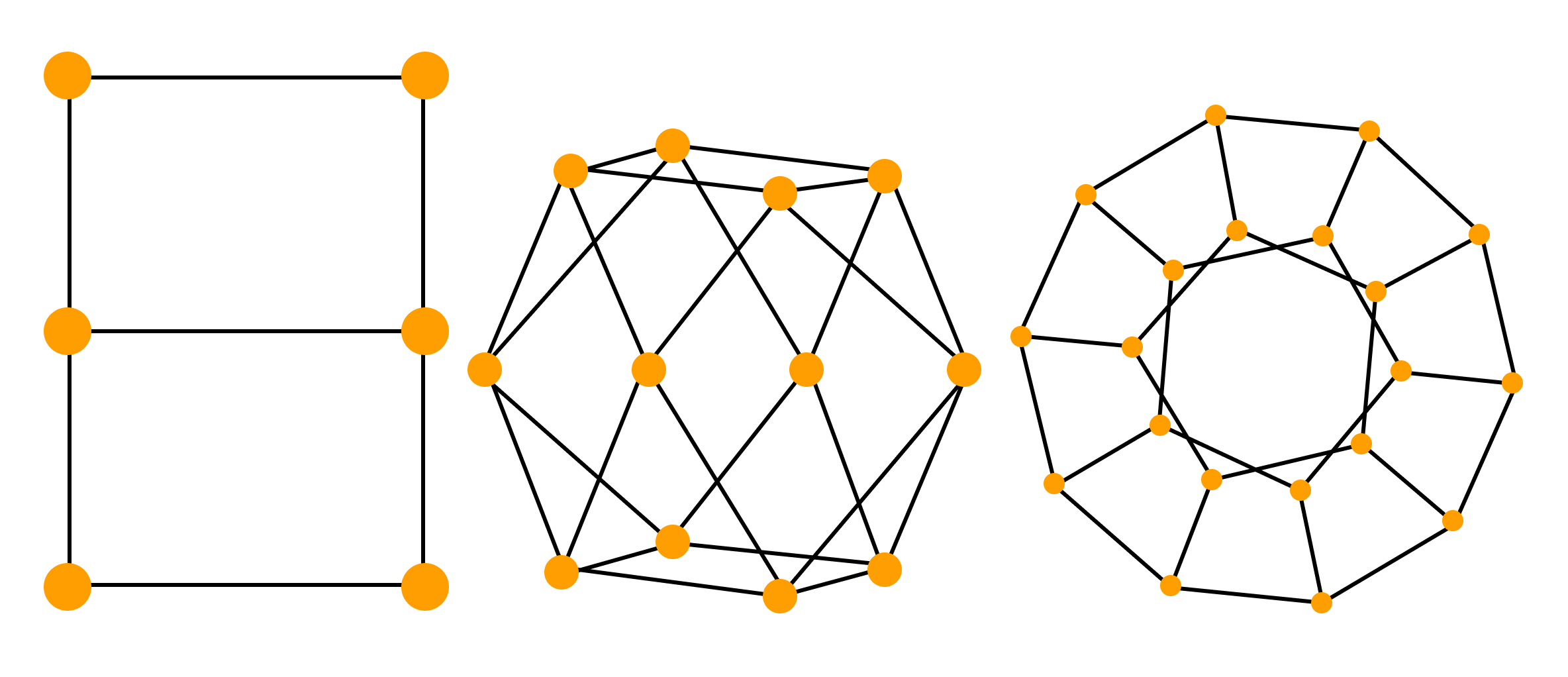
— граф называется планарным, если его можно разложить на плоскости таким образом, чтобы ребра не пересекались в точке, отличной от вершины. Если он уже так расположен, то он назьшается плоским:
Укладок планерного графа на плоскости может быть несколько
— два графа G1, G2 изоморфны, если существует взаимно однозначное отображение между множествами их вершин, сохраняющее смежность. Для орграфа должна сохраняться ориентация дуг. Для псевдографов должна сохраняться кратность дуг. Изоморфные графы могут быть получены один из другого путем перенумерации вершин (пленарные и плоские графы).
125 Достижимость и связность в графе. Определение компонент связности в неорграфах и сильных компонент в орграфах.
В неорграфе и орграфе вершина Xj достижима из вершины хi если существует маршрут, соединяющий их (для орграфа- путь). Если в орграфе существует путь из хi вXj и обратно, то говорят, что эти вершины взаимно достижимые. Неорграф называется связным, если любые 2 вершины соединены маршрутом . Орграф называется сильно связным, если любые 2 вершины взаимно достижимы. Односторонне связным, если для любой пары хi Xj по крайней мере одна достижима из другой. Слабо связным, если можно указать 2 вершины, которые недостижимы ни в одну, ни в другую стороны, а не орграф, лежащий в основе данного орграфа, является связным.
Компоненты связности неорграфа называют его максимально связный подграф, т.е. подграф, не содержащийся ни в каком другом
связном подграфе этого графа. Сильные компоненты орграфа называют максимально сильный связный подграф.
Матрицей достижимости орграфа с n вершинами называется квадратная матрица R порядка n, элементы которой определяются
следующим образом 
Матрицей контр достижимости орграфа с n вершинами называется квадратная матрица Q порядка n, элементы которой определяются: 
МатрицыR, Q, S связаны: S=Q *R .Qтранспонированная матрица R
Матрицей сильной связности орграфа с п вершинами называется квадратная матрица S порядка п, элементы которой определяются
следующим образом Sij= 1, Хj xi— взаимно достижимы (в противном случае, = 0).
После определения матрицы S, по ней можно указать сильные компоненты графа: если Ху xi принадлежат одной сильной компоненте, то Sjj = 1, при этом строки (столбцы) соответствующие данным вершинам в матрице S одинаковы. Для не орграф а матрицы S, R, Qсовпадают.
Числом вершинной связности графа б (а) называется наименьшее число вершин, при удалении которых граф становиться не связным. Числом реберной связности графа а(а) называется наименьшее число ребер, при удалении которых граф становиться не связным. Вершина xi -точка сочленения, если при ее удалении связность графа нарушается. Ребро графа называется мостом, если его удаление приводит к нарушению связности.
127 Деревья. Построение деревьев с использованием поиска в глубину и в ширину. Алгоритмы Краскала и Прима построения кратчайшего остова графа.
Деревом называется связный ациклический граф. Ориентированным деревом называется орграф без циклов, в котором существует вершина x0, из которой имеется единственный путь в любую другую вершину графа. Деревом графа G называется его связный ациклический подграф. Остовым деревом графа называется дерево графа G, содержащее все вершины этого графа (остов T).
Ребра остового дерева называются ветвями, а ребра графа G, не принадлежащие остовому дереву, называются хордами. K – деревом называется ациклический граф, состоящий из k-компонентов связи.
Остов существует в любом графе, при чем он может быть определен не единственным способом.
Для остового дерева T справедливо:
— T – связный граф, но он утрачивает связность при удалении хотя бы одного ребра
— T – ациклический граф, но добавление к нему хотя бы одного ребра приводит к появлению цикла
— любые 2 вершины остовного дерева связаны единственной простой цепью
— остовое дерево содержит, по крайней мере, 2 висячие вершины
— число ребер остового дерева на единицу меньше числа его вершин.
Для построения остового дерева связного графа могут быть использованы 2 стратегии: поиск в глубину и поиск в ширину.
При поиске в глубину построение остова начинается с произвольной вершины графа x0. Затем выбирается вершина смежная с ней, например x1 и т.д. Если на k-ом шаге поиска для вершины xk существуют смежные вершины, которые не были еще просмотрены, происходит переход в одну из этих вершин, в противном случае, происходит возврат в предыдущею вершину xk-1 и поиск продолжается от нее. В процессе поиска вершины соединяются ребрами. Поиск заканчивается, когда будут просмотрены все вершины графа и произведен возврат в x0.
| 2 3 5 6 1 4 7 10 9 |
Поиск в ширину отличается от поиска в глубину тем, что на каждом шаге просматривается не одна, а все вершины смежные с текущей.
| 2 3 6 7 1 4 10 5 9 |
Кратчайшим остовом взвешенного графа называется остов, у которого сумма всех весов ребер наименьшая. Для построения кратчайшего остового дерева взвешенного графа могут быть использованы алгоритм Краскала или алгоритм Прима.
Алгоритм Краскала заключается в следующем: на начальном этапе из всех ребер графа G выбирается и включается в остов ребро U1, имеющее наименьший вес. На каждом последующем i-ом шаге из еще не включенных в остов ребер выбирается ребро, имеющее наименьший вес и не составляющее цикл с уже имеющимися ребрами. Процесс построения остового дерева завершается, когда в него будет включено n-1 ребро (n – количество вершин графа G).
Алгоритм Прима отличается от алгоритма Краскала тем, что в процессе построения необходимо следить за связностью строящегося дерева. При этом, если дерево Ti построено, то новое ребро выбирается не из всех оставшихся ребер графа, а только из тех, которые соединяют дерево Ti с вершинами, не включенными в него.
Источник
Теория графов. Основные понятия и виды графов
О чем эта статья:
Теория графов
В переводе с греческого граф — «пишу», «описываю». В современном мире граф описывает отношения. И наоборот: любое отношение можно описать в виде графа.
Теория графов — обширный раздел дискретной математики, в котором системно изучают свойства графов.
Теория графов широко применяется в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических цепей, коммуникации, психологии, социологии, лингвистике и в других областях.
Для чего строят графы: чтобы отобразить отношения на множествах. По сути, графы помогают визуально представить всяческие сложные взаимодействия: аэропорты и рейсы между ними, разные отделы в компании, молекулы в веществе.
Давайте на примере.
Пусть множество A =
На множестве A зададим отношение знакомства между людьми из этого множества. Строим граф из точек и связок. Связки будут связывать пары людей, знакомых между собой.
Число знакомых у одних людей может отличаться от числа знакомых у других людей, некоторые могут вовсе не быть знакомы (такие элементы будут точками, не соединёнными ни с какой другой). Так получился граф:
В данном случае точки — это вершины графа, а связки — рёбра графа.
Теория графов не учитывает конкретную природу множеств A и B. Существует большое количество разных задач, при решении которых можно временно забыть о содержании множеств и их элементов. Эта специфика не отражается на ходе решения задачи.
Например, вопрос в задаче стоит так: можно ли из точки A добраться до точки E, если двигаться только по соединяющим точки линиям. Когда задача решена, мы получаем решение, верное для любого содержания, которое можно смоделировать в виде графа.
Не удивительно, что теория графов — один из самых востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может обсудить с человеком вопросы отношений, географии или музыки, решения различных задач.
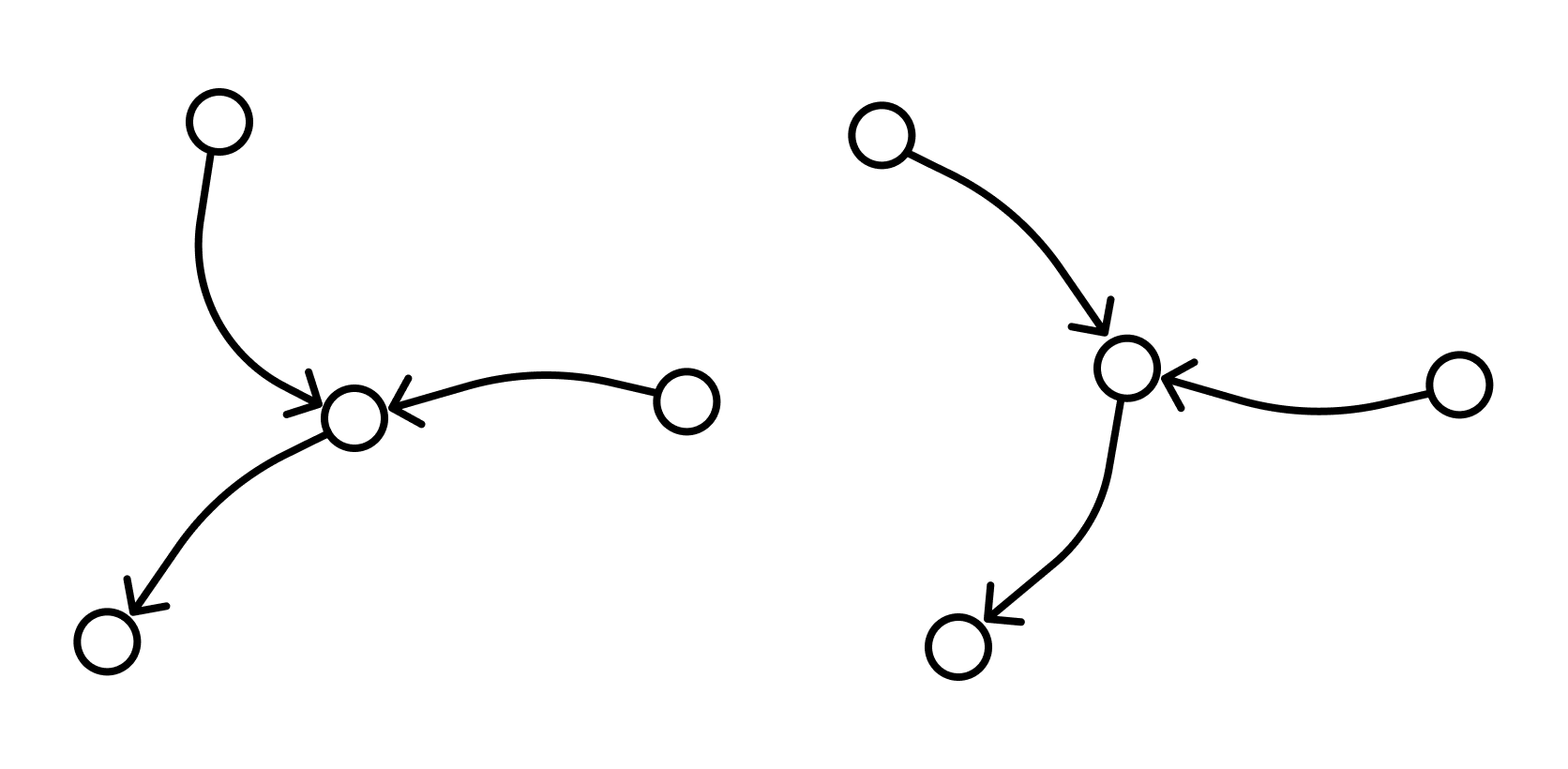
Графом называется система объектов произвольной природы (вершин) и связок (ребер), соединяющих некоторые пары этих объектов.
Пусть V — (непустое) множество вершин, элементы v ∈ V — вершины. Граф G = G(V) с множеством вершин V есть некоторое семейство пар вида: e = (a, b), где a, b ∈ V, указывающих, какие вершины остаются соединёнными. Каждая пара e = (a, b) — ребро графа. Множество U — множество ребер e графа. Вершины a и b — концевые точки ребра e.
Широкое применение теории графов в компьютерных науках и информационных технологиях можно объяснить понятием графа как структуры данных. В компьютерных науках и информационных технологиях граф можно описать, как нелинейную структуру данных.
Линейные структуры данных особенны тем, что связывают элементы отношениями по типу «простого соседства». Линейными структурами данных можно назвать массивы, таблицы, списки, очереди, стеки, строки. В нелинейных структурах данных элементы располагаются на различных уровнях иерархии и подразделяются на три вида: исходные, порожденные и подобные.
Основные понятия теории графов
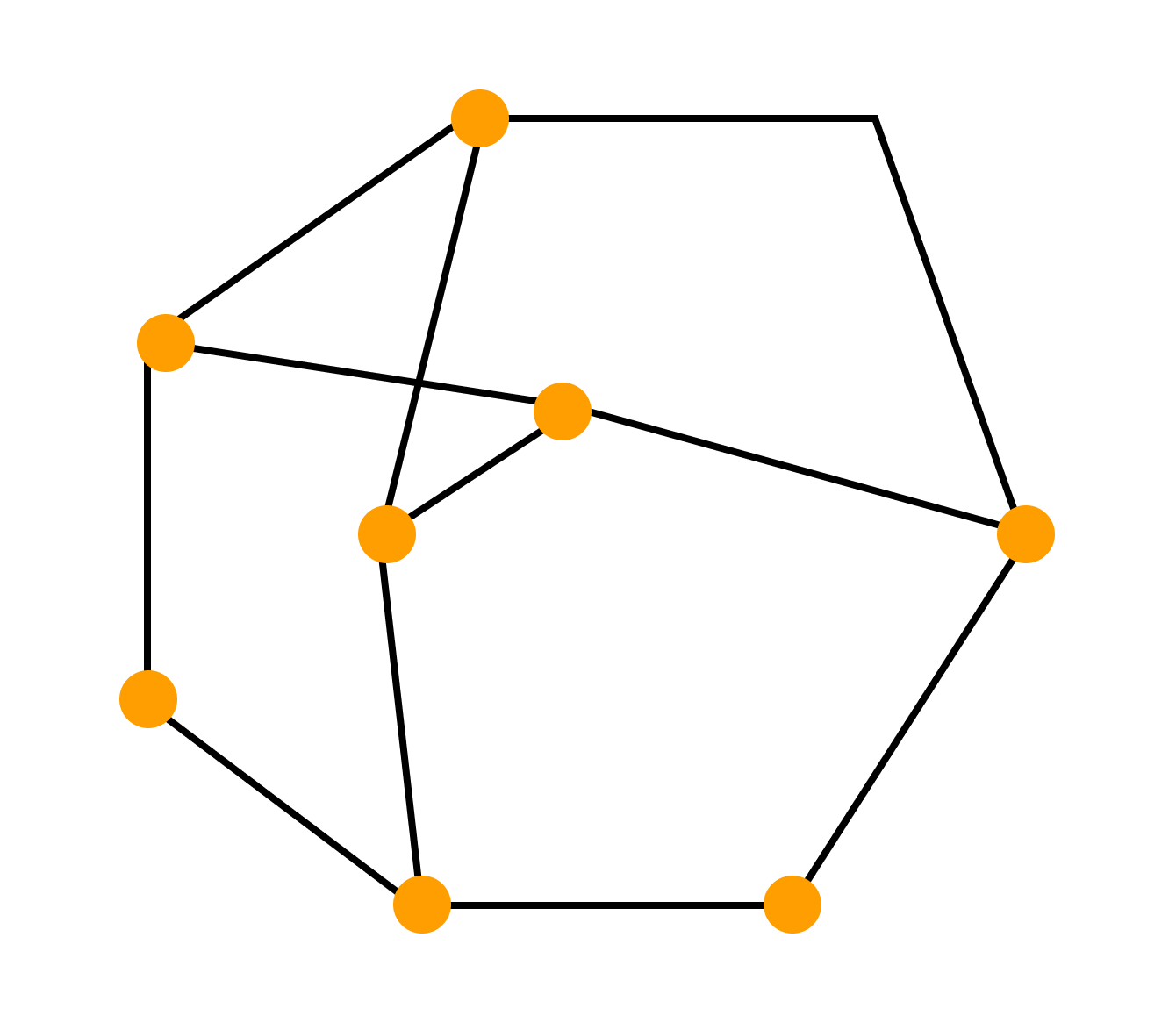
Граф — это геометрическая фигура, которая состоит из точек и линий, которые их соединяют. Точки называют вершинами графа, а линии — ребрами.
- Два ребра называются смежными, если у них есть общая вершина.
- Два ребра называются кратными, если они соединяют одну и ту же пару вершин.
- Ребро называется петлей, если его концы совпадают.
- Степенью вершины называют количество ребер, для которых она является концевой (при этом петли считают дважды).
- Вершина называется изолированной, если она не является концом ни для одного ребра.
- Вершина называется висячей, если из неё выходит ровно одно ребро.
- Граф без кратных ребер и петель называется обыкновенным.