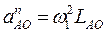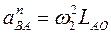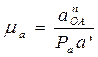Графоаналитический метод



На практике широко применяют метод планов скоростей и ускорений. Метод основан на графическом решении векторных уравнений движения. Для построения планов скоростей и ускорений механизма должна быть известна его кинематическая схема и задан закон движения входного звена.
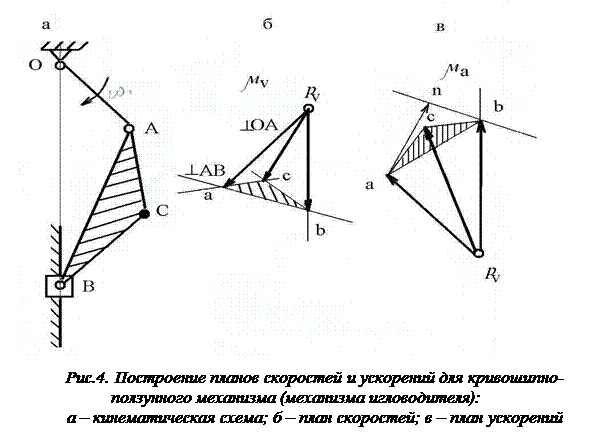
В качестве примера рассмотрим кинематику кривошипно-коромыслового механизма (механизма игловодителя швейной машины) (рис.4).
Для заданного положения механизма известны угловые скорости и ускорения входного звена. Для простоты решения задачи будем полагать, что угловое ускорение входного звена равно нулю.
Построение плана скоростей начинается с определения скорости точка А кривошипа
Вектор скорости VA направлен перпендикулярно кривошипу ОА в направлении его вращения (угловой скорости). Точка В, принадлежащая звену 2, рассматривается в относительном движении вокруг точки А. Скорость точки В можно представить как векторную сумму скоростей переносного и относительного движений. Переносным движением будем считать скорость точки А, а относительным – вращательное движение звена 2 вокруг точки А 
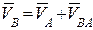
где 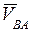
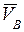
Для определения указанных неизвестных величин строим план скоростей в выбранном масштабе скорости mv. Из произвольного полюса pv (рис.4,б) проводим вектор рvа =VA/mv, перпендикулярный кривошипу ОА, соответствующий на плане скоростей абсолютной скорости VA. Из конца вектора рvа (точка а) проводим линию в направлении относительной скорости 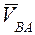
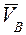

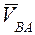
Для определения скорости точки С шатуна можно воспользоваться известной из теоретической механики теоремой подобия для скоростей, согласно которой отрезки прямых линий, соединяющие точки на схеме звена механизма и отрезки прямых линий, соединяющие концы векторов относительных скоростей этих точек на плане скоростей, образуют подобные фигуры. Фигура на плане скоростей повернута относительно фигуры схемы звена на 90° (свойство планов скоростей).
Вектор рvс скорости точки С находим построением на отрезке ab треугольника abc , подобного треугольнику ABC, повернутому на 90°. Для этого из точки а плана скоростей проводим линию, перпендикулярную АС, а через точку b – перпендикулярную ВС. Значение скорости в этой точке вычисляем по формуле
Угловая скорость звена 2
Направление w2 находится по вектору скорости VBA.
Планы скоростей механизмов позволяют охарактеризовать движение механизма:
– векторы, выходящие из полюса плана скоростей (рv) , представляют собой абсолютные скорости;
– вектор, соединяющий концы абсолютных скоростей, представляют собой относительную скорость; он направлен к той точке, которая стоит первой в индексе скорости;
– план скоростей дает возможность находить касательные к траекториям точек механизма, не выстраивая этих траекторий;
– полюс плана скоростей (рv) соответствует мгновенному центру вращения звена (МЦВ).
Построение плана ускорений начинают с построения абсолютного ускорения aA точки А кривошипа, складывающегося геометрически из суммы нормальной (aA n = w1 2 ∙lOA) тангенциальной (aA t = e1∙lOA) составляющих:
aA = aA n + aA t 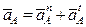
При 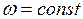
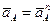
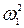
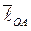
Ускорение точки В находим из уравнения
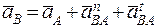
Значение нормальной составляющей относительного ускорения определяется по формуле
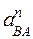
Вектор 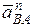
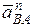
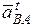
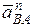
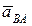

Перенося вектор ускорения 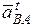
Вектор рас ускорения точки С находим, используя свойство плана ускорений, построением на отрезке ab треугольника abc, подобного треугольнику АВС, повернутого на угол (180° — a), где
Значение ускорения в этой точке равно аC = ma∙раc.
План ускорений имеет следующие характеристики:
· векторы, выходящие из полюса ра плана ускорений, представляют собой абсолютные ускорения соответствующих точек звеньев механизма;
· отрезки, расположенные между концами векторов абсолютных ускорений, соответствуют полным относительным ускорениям;
· концы векторов абсолютных ускорений точек, принадлежащих одному звену механизма, на плане ускорений образуют подобные фигуры, повернутые на угол (180° — a);
· план ускорений позволяет находить угловые ускорения звеньев.
Вопросы для самопроверки:
1. Сформулируйте задачи и назовите методы кинематического анализа рычажных механизмов?
2.Как строятся крайние положения и траектории точек звеньев механизма?
3.Постройте план скоростей и ускорений кривошипно-коромыслового и кривошипно-ползунного механизмов.
4.Запишите формулу ля вычисления угловых скоростей и ускорений. Определите их направление.
5 Как следует определять скорость (ускорение) третьей точки звена при известных векторах скоростей (ускорений) двух точек звена, используя свойство
Источник
Графоаналитический метод кинематического анализа
Графоаналитический метод называют методом планов скоростей и ускорений.
Задача о положениях решается графическим методом, то есть построением нескольких совмещённых планов механизма в выбранном масштабе длин.
Задачи о скоростях и ускорениях решаются построением планов скоростей и ускорений звеньев механизма при определённых (заданных) положениях ведущего звена на основе заранее составленных векторных уравнений скоростей и ускорений звеньев механизма.
Преимущество этого метода по сравнению с графическим в том, что он менее трудоёмок, так как позволяет определять скорости и ускорения (их величину и направление) на одном плане скоростей или плане ускорений для множества точек механизма.
Недостатком метода является то, что требуется построить планы скоростей и ускорений для нескольких положений механизма (если необходимо определять скорость и ускорение при различных положениях механизма и его звеньев).
Планы скоростей и ускорений шарнирного четырёхзвенник
При решении задач такого типа известны угловая скорость w1 ведущего звена 1 – кривошипа, длины звеньев и координаты неподвижных точек.
Последовательность решения задачи:
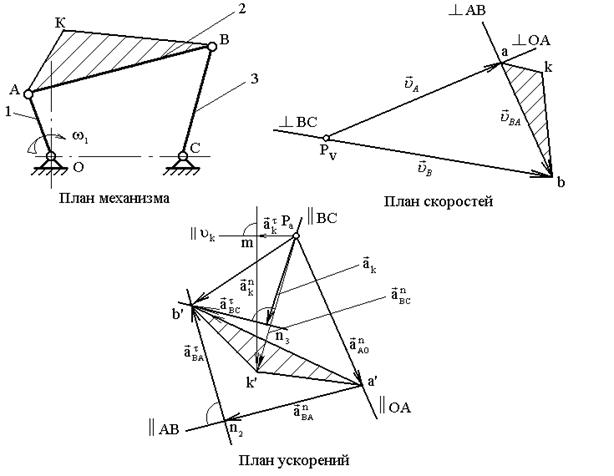
1. Строится план механизма (рис. 2.2) в выбранном масштабе длин:
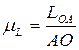
где LOA – длина кривошипа, м; AO – длина отрезка, изображающего кривошип на плане механизма, мм.
Для построения плана механизма остальные длины звеньев и координаты неподвижных точек шарнирного четырехзвенника (рис. 2.2) переводятся масштабом длин mL в отрезки:
2. Составляются векторные уравнения линейных скоростей отдельных точек, принадлежащих звеньям механизма.
Векторное уравнение для звена 2 (шатуна)
где VА = VАО – скорость точки А, которая равна скорости точки А относительно оси вращения кривошипа точки О; VВА – вектор относительной скорости точки В шатуна относительно А имеет направление, перпендикулярное отрезку АВ на плане механизма.
Векторное уравнение для звена 3 (коромысла)
Так как точка С (ось вращения коромысла 3) неподвижна, то её скорость равна нулю (VС = 0), а вектор относительной скорости точки В относительно С (VВС) имеет направление, перпендикулярное отрезку ВС на плане механизма.
3. Строится план скоростей механизма – это не что иное, как графическое изображение на чертеже векторных уравнений (2.1) и (2.2) в каком-либо масштабе.
План скоростей механизма и его свойства
План скоростей желательно строить рядом с планом механизма (рис. 2.2). Предварительно рассчитывается скорость точки А кривошипа:
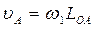
Затем выбирается масштаб плана скоростей mu по соотношению
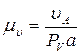
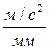
где uA – скорость точки А, м/с; PVa – длина отрезка, изображающего на будущем плане скоростей скорость VA, выбирается произвольной длины в мм; при выборе желательно придерживаться условий: во-первых, план скоростей должен размещаться на отведённом месте чертежа, во-вторых, численное значение масштаба mu должно быть удобным для расчётов (mu должно быть круглым числом).
После этого можно приступать к построению плана скоростей механизма. Его следует проводить в последовательности, соответ-ствующей написанию векторных уравнений (2.1) и (2.2).
Сначала проводится из произвольно выбранной рядом с планом механизма точки Рu (полюса плана скоростей) вектор скорости VА, который перпендикулярен отрезку ОА на плане механизма и имеет длину PVa, выбранную нами при определении масштаба плана скоростей mu. Затем через точку a проводится линия, перпендикулярная отрезку АВ плана механизма, а через полюс PV – линия, перпендикулярная отрезку ВС. Пересечение этих линий даёт точку b. В соответствии с векторными уравнениями (2.1) и (2.2) на построенном плане наносятся направления (стрелки) векторов VВиVВА.
Определим скорость точки К, принадлежащей шатуну. Для неё можно записать векторные уравнения скоростей:
где вектор скорости VКА перпендикулярен отрезку АК на плане механизма, а вектор VКВ – отрезку КВ.
Построением этих векторных уравнений получаем точку k на плане скоростей. При этом из точки a плана скоростей проводим линию, перпендикулярную отрезку АК, а через точку b плана скоростей – линию, перпендикулярную отрезку ВК плана механизма. Величину скорости точки К можно вычислить по формуле
где РVk – длина соответствующего вектора на плане скоростей.
Можно заметить, что треугольники на плане скоростей и плане механизма подобны:
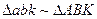
так как стороны их взаимно перпендикулярны. Это свойство можно использовать для определения скорости любой другой точки, принадлежащей какому-либо звену механизма. Отсюда следует теорема подобия: отрезки относительных скоростей на плане скоростей образуют фигуру, подобную фигуре соответствующего звена на плане механизма. Стороны фигур взаимно перпендикулярны.
Угловые скорости шатуна 2 и коромысла 3 рассчитываются по формулам
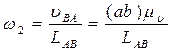
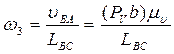
Направления угловых скоростей определяются по направлениям векторов VВАиVBC. Для этого вектор VВА условно переносится в точку В плана механизма. Куда он будет вращать шатун 2 относительно точки А, в ту сторону и будет направлена угловая скорость шатуна ω2.
Аналогично поступают со скоростью VВА. В каком направлении будет вращаться коромысло относительно точки С, туда и будет направлена угловая скорость ω3.
План ускорений механизма и его свойства
Последовательность построения плана ускорений рычажного механизма аналогична построению плана скоростей. Рассмотрим её на примере механизма шарнирного четырехзвенника (рис. 2.2). Примем угловую скорость кривошипа постоянной (w1 = const, что является наиболее распространённым и рациональным видом движения в реальных механизмах).
Векторное уравнение ускорений для звена 1 (кривошипа)
где нормальная составляющая ускорения точки A относительно O рассчитывается по формуле 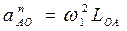
Вектор а n АО параллелен отрезку АО на плане механизма. Тангенциальная составляющая ускорения а t АО рассчитывается по формуле
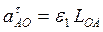
В нашем случае угловое ускорение кривошипа e1 = 0, тогда 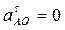
Векторное уравнение ускорений для звена 2 (шатуна)
где нормальная составляющая ускорения точки В относительно точки А рассчитывается по формуле 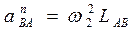
Вектор а n ВА параллелен отрезку АВ и направлен от В к А, а тангенциальная составляющая а t ВА перпендикулярна АВ.
Векторное уравнение ускорений для звена 3 (коромысла)
где ускорение точки С аС = 0; нормальная составляющая ускорения точки В относительно точки С рассчитывается по формуле 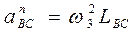
Вектор а n ВС направлен параллельно отрезку ВС плана механизма от В к С, а вектор а t ВС – перпендикулярно ВС.
Выбираем масштаб плана ускорений: 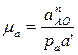
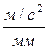
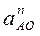
Тогда ускорение а n ВА будет изображаться на плане ускорений вектором, имеющим длину 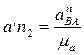
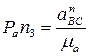
Затем строится план ускорений (рис. 2.2) с использованием составленных векторных уравнений ускорений. Из произвольно выбранного полюса Ра параллельно отрезку ОА плана механизма проводится вектор ускорения 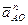
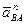
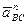
Используя план ускорений, можно вычислить ускорения
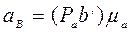
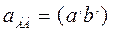
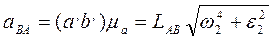
где w2 и e2 – угловые скорость и ускорение шатуна.
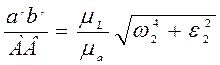
где w2 и e2 не зависят от выбора (расположения) полюса Ра плана ускорений, а отношение масштабов постоянно (mL/ma= const) для данного плана ускорений. Поэтому для любой точки (например, К, принадлежащей шатуну) можно записать пропорции
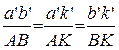
Отсюда формулируется теорема подобия: отрезки полных относительных ускорений на плане ускорений образуют фигуру, подобную соответствующей фигуре звена на плане механизма.
Величину ускорения точки К можно вычислить по формуле
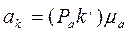
Угловые ускорения звеньев шатуна 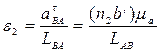
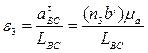
Так как w2 и e2 направлены в противоположные стороны, вращение шатуна является замедленным.
Использование плана скоростей и плана ускорений
для определения радиуса кривизны траектории движения точки
Радиус кривизны траектории движения точки (например, точки К) можно вычислить по формуле
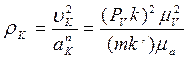
где а n К – нормальная составляющая ускорения точки К.
Для определения величины (и направления) а n К следует вектор полного ускорения аК на плане ускорений разложить на нормальную и тангенциальную составляющие, причём а n К перпендикулярна вектору скорости VК, а t К параллельна последнему. Для этого сначала через полюс плана ускорений Ра проводится прямая, параллельная вектору скорости точки К, а через точку k` – перпендикуляр к этой прямой; на их пересечении получают точку m.
Использование плана скоростей и плана ускорений
для определения мгновенного центра скоростей (МЦС)
и мгновенного центра ускорений (МЦУ) звена
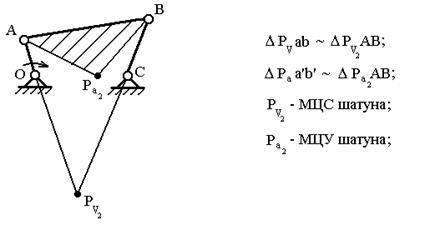
Для определения МЦС и МЦУ используют теорему подобия, а на плане механизма строят фигуры, подобные фигурам (треугольникам) на планах скоростей и ускорений (рис. 2.3).
Рис. 2.3. Определение положений мгновенных центров скоростей PV2
Из теоретической механики известно, что плоскопараллельное движение звена механизма в каждый момент времени может быть представлено как вращение вокруг некоторой точки, которую называют мгновенным центром вращения или мгновенным центром скоростей (МЦС). Если данная точка относится к станине (стойке) механизма, т.е. является неподвижной, то соответствующий МЦС называют мгновенным центром скоростей в абсолютном движении рассматриваемого звена. Таким образом, если мы представим, что точка PV2 принадлежит шатуну (рис. 2.3), то её скорость будет равна нулю.
Если же рассматривается движение звена относительно любого подвижного звена механизма, то соответствующий МЦС называют мгновенным центром скоростей в относительном движении рассматриваемых звеньев.
Аналогично может быть найдена условная точка, принадлежащая звену, абсолютное ускорение которой в данный момент времени равно нулю. Эта точка называется мгновенным центром ускорений (МЦУ) звена. Если звено механизма совершает сложное плоскопараллельное движение, то меняются и положения МЦС и МЦУ.
Планы скоростей и ускорений кривошипно-ползунного механизма
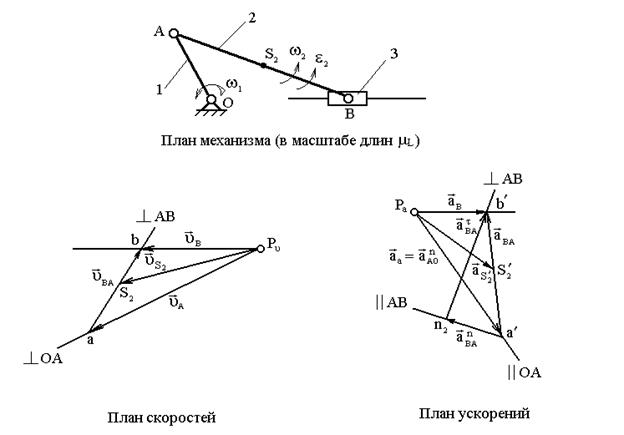
Последовательность построения планов скоростей и ускорений кривошипно-ползунного механизма (рис. 2.4) аналогична той, которая приведена в предыдущем случае. В дальнейшем некоторые подробности (расчёты масштабов, длин mе, масштабов планов скоростей mv и ускорений mа и т.д.) будут пропущены.
План скоростей кривошипно-ползунного механизма начинают строить после построения плана механизма в заданном положении, в выбранном масштабе длин mL, составления векторного уравнения скоростей и выбора масштаба плана скоростей mv.
Векторное уравнение скоростей шатуна 2 (рис. 2.4)
где VА = w1 LOA – скорость точки А, м/с; вектор этой скорости направлен перпендикулярно прямой ОА кривошипа 1 (рис. 2.4) на плане механизма; VВА – вектор скорости точки В относительно А; имеет направление, перпендикулярное прямой АВ на плане механизма; VВ – вектор полной (абсолютной), скорости ползуна 3; должен быть параллельным направлению движения ползуна.
Для построения плана скоростей сначала из полюса плана Рv (рис. 2.4) проводится вектор скорости точки А относительно О – VА, т.е. векторный отрезок Рva. Затем через точку апроводится перпендикуляр к прямой АВ плана механизма и через полюс Рv – прямая, параллельная движению ползуна 3. На пересечении этих двух прямых получается точка b. Направления векторов скоростей VВ иVВА обозначают стрелками.
Например, необходимо определить скорость точки S2, принадлежащей шатуну 2 и расположенной на середине отрезка АВ. Используя теорему подобия, на отрезке ab плана скоростей находят его середину (точка S2), которая, будучи соединенной с полюсом Рv, даст вектор VS2, изображающий абсолютную (полную) скорость точки S2.
и ускорений кривошипно-ползунного механизма
Рассчитаем величину линейных скоростей и угловую скорость шатуна:
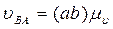
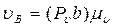
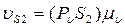
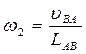
Направление вектора угловой скорости шатуна w2 определяется следующим образом. Вектор скорости VВА условно переносится в точку В плана механизма. Куда он будет вращать шатун относительно точки А, в ту сторону и направлена угловая скорость w2 шатуна.
План ускорений кривошипно-ползунного механизма строят после того, как будет составлено векторное уравнение ускорений шатуна, учитывая, что он совершает сложное движение:
где аА – ускорение точки А; его величину и направление можно определить, используя векторное уравнение ускорения точки А относительно оси О вращения кривошипа:
причём ускорение точки А относительно О можно разложить на две составляющие – нормальное ускорение а n АО и тангенциальное а t АО, т.е.
Так как точка О неподвижна и ускорение её равно нулю (аО= 0 и а t АО = 0 при условии, что угловая скорость вращения кривошипа постоянна: w1 = const и его угловое ускорение e1 = 0), то векторное уравнение ускорения точки А можно записать в виде
Величина нормальной составляющей ускорения (нормальное ускорение) рассчитывается по формуле
(его вектор направлен по радиусу вращения кривошипа от точки А к точке О).
Затем вычисляется нормальное ускорение точки В относительно А по формуле
(его вектор направлен от В к А).
После выбора масштаба плана ускорений по формуле
величина нормального ускорения a n BA переводится этим масштабом в векторный отрезок длиной
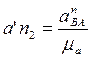
Затем строится план ускорений (см. рис. 2.4). Из произвольно выбранного полюса Ра параллельно отрезку ОА плана механизма проводится вектор ускорения a n AО, длина которого 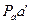
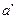
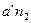
Для нахождения величины ускорения точки S2, принадлежащей шатуну, можно применить теорему подобия. При этом необходимо на векторе, изображающем на плане ускорений относительное ускорение aBA, найти соответствующую точку S2‘, делящую отрезок a’b’ в той же пропорции, что и точка S2 делит отрезок АВ на плане механизма.
Угловое ускорение шатуна вычисляется по формуле
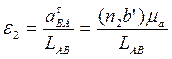
где n2b’ – длина вектора на плане ускорений, изображающего тангенциальное ускорение а 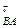
Для определения направления вектора углового ускорения шатуна e2 необходимо вектор тангенциального ускорения а 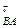
Планы скоростей и ускорений кулисного механизма
Чтобы построить план скоростей, необходимо составить векторное уравнение скоростей. При этом следует иметь в виду, что точка А1 (рис. 2.5), принадлежащая кривошипу 1, и точка А2, принадлежащая ползуну 2 и совпадающая на плане механизма с точкой А1, вращаются вокруг оси О с одинаковыми линейными и угловыми скоростями:
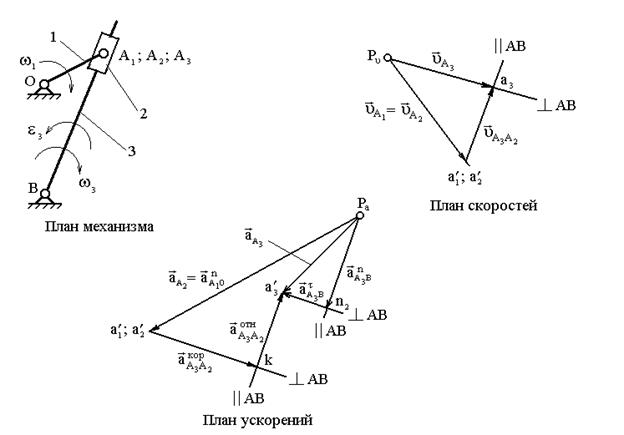
Если задана величина w1, то величину линейной скорости рассчитывают по формуле
Векторы скоростей VА1 иVА2 направлены перпендикулярно радиусу ОА1. Скорость точки А3, принадлежащей кулисе 3, можно найти по векторному уравнению скоростей
где VА3А2 – вектор скорости точки А3 кулисы относительно точки А2 ползуна, параллельный прямой А1В плана механизма.
После выбора масштаба плана скоростей mv (см. предыдущие примеры механизмов) строят план скоростей. Из полюса Рv (см. рис. 2.5) перпендикулярно отрезку ОА плана механизма проводится вектор скорости VА1, совпадающий с вектором скоростиVА2 (см. рис. 2.5, вектор 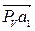
Вычисляют величины скоростей:
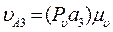
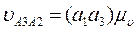
где Рv a3 и а1 а3 – длины векторов, измеренные на плане скоростей.
Дата добавления: 2016-06-09 ; просмотров: 4757 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник