- Графоаналитический способ решения задач.
- Графоаналитический способ решения задач
- Графоаналитический метод расчета трубопроводов
- 2. Порядок определения пропускной способности трубопровода графоаналитическим методом.
- 3. Тенденции в истории развития нефтедобычи
- 13 Билет
- 1. Несовершенство скважин и его учет.
- Гидравлический расчет простых напорных трубопроводов
Графоаналитический способ решения задач.
Определение пропускной способности трубопровода по заданным параметрам его и жидкости, а также определение минимального диаметра трубопровода по заданным напору, параметрам жидкости и трубопровода, пропускной способности проводится графоаналитическим методом.
Рассмотрим алгоритм решения задач этого типа на примере первой задачи.
Графоаналитический способ решения основан на предварительном построении графической зависимости hT=f(Q) — гидравлической характеристики трубопровода (рис.4.1). Для этого:
1. Последовательно задаемся рядом произвольных значений Q.
2. Находим соответствующие средние линейные скорости ω.
3. Рассчитываем соответствующие параметры Re.
4. Рассчитываем соответствующие параметры λ.
5. Для каждого принятого значения Q находим потери напора hT.
6. По полученным данным строим график hT = f(Q).
7. Отложив на оси ординат известное значение H, на оси абсцисс находят соответствующее ему искомое значение Q.
Аналогично решается и вторая задача:
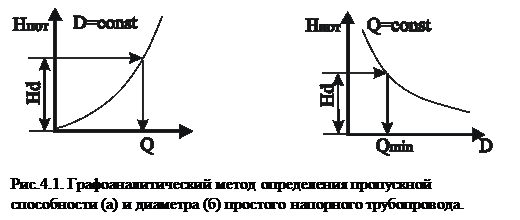 |
Задаются рядом d, находят для них hT, строят график hT = f(d) и по заданной величине Hпо графику находят соответствующее ему значение d.
Дата добавления: 2015-05-19 ; просмотров: 1352 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Графоаналитический способ решения задач
Определение пропускной способности трубопровода по заданным параметрам его и жидкости, а также определение минимального диаметра трубопровода по заданным напору, параметрам жидкости и трубопровода, пропускной способности проводится графоаналитическим методом.
Рассмотрим алгоритм решения задач этого типа на примере первой задачи.
Графоаналитический способ решения основан на предварительном построении графической зависимости hT=f(Q) — гидравлической характеристики трубопровода. Для этого:
1. Последовательно задаемся рядом произвольных значений Q.
2. Находим соответствующие средние линейные скорости ω.
3. Рассчитываем соответствующие параметры Re.
4. Рассчитываем соответствующие параметры λ.
5. Для каждого принятого значения Q находим потери напора hT.
6. По полученным данным строим график hT = f(Q).
7. Отложив на оси ординат известное значение H, на оси абсцисс находят соответствующее ему искомое значение Q.
Аналогично решается и вторая задача:
Задаются рядом d, находят для них hT, строят график hT = f(d) и по заданной величине H по графику находят соответствующее ему значение d.
Потери напора на трение в трубопроводе определяются по формуле Дарси-Вейсбаха (70).
Разновидностью этого выражения, часто применяемой при технологических расчетах трубопроводов, является формула академика Лейбензона:

где Q и ν — соответственно объемный расход и кинематическая вязкость перекачиваемой жидкости;
β, А, m- коэффициенты, зависящие от режима течения жидкости.
Формула (90) в явной форме выражает зависимость h от Q и получается из выражения (70) при условии, что λ определяется выражением вида

Формулы для расчета коэффициента гидравлического сопротивления в зависимости от режима течения приведены в табл. 8.
Потеря напора на единицу длины трубопровода называется гидравлическим уклоном:

Для наглядности и представления о гидравлическом уклоне сделаем построение гидравлического треугольника: отложим от начальной А’ и конечной B’ точек на профиле трассы трубопровода статические (пьезометрические) напоры 

Из построения следует, что гидравлический уклон является тангенсом угла наклона этой прямой к горизонту:

то есть i = const.
Величина 
Таблица 8
Формулы для расчета коэффициента гидравлического сопротивления
| Ламинарный режим | Турбулентный режим |
| Re Перед началом гидравлического расчета исследуется профиль трассы трубопровода для определения на нем перевальных точек и нахождения его расчетной длины. Эта длина может быть значительно меньше геометрической, а перевальная точка не обязательно является наивысшей точкой трассы. Достаточно закачать жидкость на перевальную точку, чтобы она самотеком достигла конца трубопровода. Гидравлические расчеты сложных трубопроводов Различают четыре категории сложных трубопроводов. I. Коллектор постоянного диаметра с распределенным по длине отбором продукции (раздаточный коллектор в резервуарах, отстойниках, сепараторах). II. Сборный коллектор переменного диаметра с распределенным по длине поступлением продукции (система сбора скважинной продукции). III. Коллектор с параллельным участком трубопровода (байпас на водоводах). IV. Замкнутый коллектор (кольцевой водовод). Источник Графоаналитический метод расчета трубопроводов
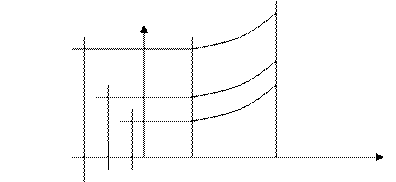
Графоаналитический метод расчета трубопроводов основан на построении характеристик трубопровода и кривых потребного напора. Характеристикой трубопровода называется зависимость потерь напора от расхода. ∆z ламинарный турбулентный режим В общем случае задавая различные значения и подставляя значения расхода в формулы потерь напора получаем значения потерь напора и строим график. Потребным напором называется напор в начале сечения трубопровода, необходимый для перемещения жидкости от начального до конечного сечения. Pк/ρg – остаточный свободный напор; zк — zн + Pк/ρg – приведенный геометрический напор. Приведенный геометрический напор может быть как положительной, так и отрицательной величиной. Поэтому график потребного напора располагается равноудалено от характеристики трубопровода. График потерь напора и характеристик трубопровода – только для простого трубопровода. Для сложного находится построением. Рассмотрим последовательное соединение. Последовательное соединение. Q = const; h = h1 + h2 Параллельное соединение. h = const; Q = Q1 + Q2 Источник 2. Порядок определения пропускной способности трубопровода графоаналитическим методом.Задается рядом произвольные значения q, затем находим среднюю скорость патока (wi=Qi/S=Qi/0,785d*dтр), рассчитаем критерии Re=wdр/М, определяем коэффициент гидравлического сопротивления (λ=64/Re при Re=2320; λ=0,3164/Re^0,25, при Re>2320). Затем для каждого расхода находим ∆Н и строим график зависимости. В зависимости от Н зад находим Qзад. 3. Тенденции в истории развития нефтедобычи1. Отказ от законтурного заводнения и переход на вариант внутри-контурного (Усть-Балык) 2. Внедрение в 70-е годы циклического заводнения (Трехозерка) 3. разукрупнение экспл. Объектов 4. Использование в системе ППД насосов с повышенными давлениями закачки (от 1—0120 до 150-18 атм.) 5.Создание блочно-замкнутых систем заводнения в вариантах. Перевод высоко обводненного фонда под закачку в целях создания поперечных рядов в бывших 3-х рядных системах. Создание блочно-замкнутых систем на ранней стадии осовения месторождения (СибНИИНП) 6. Переход от рядных систем заводнения на площадные (обычно от3-х рядок к 7-точечной и реже наоборот) 7. Использование очагового и избирательного заводнений, чаще в условиях 5-ти рядных систем заводнения 8. начиная с 90-х годов активная интенсификация добычи за счет внедрения ГРП и ГС 9. Уплотнение сеток скважин (до 6.3 г/СКВ) 10. Широкое внедрение физико-химических технологий (потоко-отклоняющие технологии) 11. внедрение в эксплуатационные скважины струйных насосов (тандем с УЭЦН) 12. Широкое внедрение диспергаторов и газосепараторов, где высокий газовый фактор 13. Создание и использование высоко-напорных, но низкопроизводительных ЭЦН для глубокозалегающих юрских залежей 13 Билет1. Несовершенство скважин и его учет.Гидродинамическое несовершенство скважины проявляется в том, что в призабойной зоне пласта с конечной мощностью отсутствует радиальность потока по причине, обусловленной конструкцией забоя или фильтра. Различают два вида несовершенства скважин — несовершенство по степени вскрытия и несовершенство по характеру вскрытия. Несовершенная скважина по степени вскрытия — это скважина с открытым забоем, вскрывшая пласт не на всю мощность, а частично (рис. б). Скважина, хотя и доведённая до подошвы пласта, но сообщающаяся с пластом только через отверстия в колонне труб, в цементном кольце или в специальном фильтре, называется несовершенной по характеру вскрытия пласта (рис. в). На практике чаще всего встречаются скважины несовершенны как по степени, так и по характеру вскрытия пласта (рис. г) При расчете дебита скв их гидродинамическое несовершенство учитывается введением в ф-лу Дюпюи коэф-та дополнительных фильтрационных сопротивлений С: Величина коэф-та дополнительных фильтрационных сопротивлений зависит от степени вскрытия пласта, плотности перфорации, длины и диаметра перфорационных каналов. Обычно ее определяют, используя графики И. В. Щурова. Ф-лу можно представить с использованием понятия приведенного радиуса скважины rс.пр.: Qнс=2πkh(Pк-Рс)/μ(lnRк/rc+С1+С2), k – коэф. проницаемости, μ — вязкость, h — толщина пласта, C1-доб.филтр.сопр. за счет несов.скв. по степени вскрытия. C2— по хар-ру вскрытия. С1 и С2 определяются по графикам Щурова. С1=f(hD; d/D; l1/D), где D – диаметр скважины по долоту, h – число перфорационных отверстий на 1 м, d – диаметр перф. отверстий, l1 – глубина проникновения пуль в породу. C2=f(относительного вскрытия пласта; отношения эффективной мощности пласта к диаметру по долоту) Если гидродинамическое несовершенство скв хар-ризовать отношением ее дебита к дебиту гидродинамически совершенной скв в равных условиях, то η=Qнс/Qc=ln(Rк/rc)/ln(Rк/rc.пр.), где η- коэф-т гидродинамического несовершенства скв. Источник Гидравлический расчет простых напорных трубопроводов
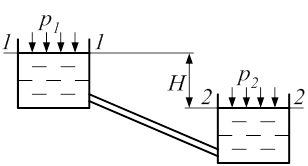
Вопросы по теме 5. 1 . По каким формулам определяются потери напора в трубах по длине и в местных сопротивлениях? 2. От каких безразмерных величин может зависеть коэффициент гидравлического сопротивления? 3. Каковы границы зон сопротивления при турбулентном течении? 4. Что такое эквивалентная и приведенная длины и когда они употребляются? Простым называется трубопровод, не имеющий ответвлений и с постоянными по длине диаметром и расходом. Длинным считается трубопровод, в котором потери напора в местных сопротивлениях малы по сравнению с потерями напора на трение по длине. В этом случае первыми или пренебрегают, или учитывают их через суммарную эквивалентную длину å lэкв , составляющую обычно 1—5 % от реальной длины трубопровода. В коротком трубопроводе оба вида потерь напора соизмеримы. Самотечным называется трубопровод, перемещение жидкости в котором происходит только за счет сил тяжести. Рис. 6.1. Схема самотечного трубопровода При гидравлическом расчете трубопроводов используются уравнение Бернулли (2.10), уравнение неразрывности и все понятия и формулы, рассмотренные в гл. 4. Такой расчет может быть сведен к решению одной из трех основных задач. Задача 1. Определение необходимого действующего напора по заданным параметрам трубопровода и жидкости . В качестве примера рассмотрим трубопровод на рис. 6.1. Пусть жидкость с заданными свойствами (ρ, v или η) должна перетекать из верхнего резервуара в нижний (уровни в которых считаются постоянными) с заданным расходом Q по трубопроводу с известными параметрами l, d, D, åz или å lэкв. Давления р1 и р2 на свободных поверхностях жидкости известны. Примем, например, что p1 = р2 =pа. Определить требуемый действующий напор. Решение. Уравнение Бернулли для живых сечений, проходящих по свободным поверхностям жидкости в резервуарах, с учетом того, что p1 = р2 и u1 » u2 » 0 (из-за больших площадей живых сечений) принимает вид где u — скорость жидкости в трубопроводе. Оно решается методами, рассмотренными в гл. 4. Задача 2. Определение пропускной способности трубопровода Q по заданным параметрам его и жидкости. Рассмотрим методику решения этого типа задач на примере рис. 6.1, но при заданном значении H и неизвестном значении Q. Решение. Уравнение Бернулли по-прежнему имеет вид (6.1), но определению подлежит uтр, связанная с расходом соотношением Q= uтр sтр. В общем случае решение этого уравнения относительно uтрзатруднено, так как неизвестен вид зависимости и l и åz от Re, a следовательно, и от uтр . Для преодоления этих трудностей существуют два способа — аналитический и графоаналитический. Аналитически задача решается методом последовательных приближений. Он особенно прост и удобен, если в результате анализа исходных данных можно предположить или ламинарный режим движения, или квадратичную зону сопротивления. Ориентировочным признаком первого является высокая вязкость жидкости, второго — малая вязкость жидкости, значительная относительная шероховатость труб. Исходя из этих предположений, выражают l по формулам (5.3) или (5.7), а затем уравнение (6.1) разрешают относительно uтр . Для проверки правильности решения определяют Re и сравнивают его со значениями Reкр или 500 Задача аналитически легко решается при помощи ЭВМ, в том числе и таких простых, как программируемые микрокалькуляторы. Графоаналитический способ решения основан на предварительном построении графической зависимости hпот=hпот(Q), называемой гидравлической характеристикой трубопровода. Для этого последовательно задаются рядом произвольных значений Q, по которым, используя схему Q®u ® Re®l® hпот, вычисляют соответствующие им значения hпот. По этим данным строится график hпот = hпот (Q) (рис. 6.2), отложив на оси ординат которого известное значение Hд, на оси абсцисс находят соответствующее ему искомое значение Q. Задача 3. Определение минимально необходимого диаметра трубопровода по заданным действующему напору, параметрам жидкости и трубопровода, а также по его требуемой пропускной способности.
Рассмотрим эту задачу на примере рис. 6.1. Аналитическое решение при ручном счете затруднено, так как в уравнение (6.1) искомый диаметр входит не только явно, но и косвенно (от него зависят u, l и z ). При графоаналитическом способе, задаваясь рядом значений d и вычисляя по ним hпот, строят по этим данным графическую зависимость hпот = hпот (d) и по этому графику (рис. 6.3) определяют значение d, соответствующее заданной величине Hд. Источник |









 h
h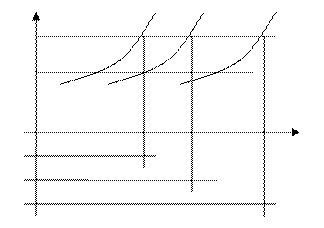 h I II
h I II
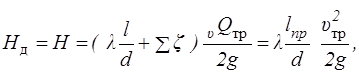 (6.1)
(6.1)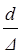 , в зависимости от выдвинутого предположения. Если предположение подтвердилось, определяют Q, если нет, то выдвигают уточненное предположение, расчет повторяется и т.д.
, в зависимости от выдвинутого предположения. Если предположение подтвердилось, определяют Q, если нет, то выдвигают уточненное предположение, расчет повторяется и т.д.



