Графоаналитическим способом
Определение площадей
Этот способ заключается в том, что здесь также в извилистый контур вписываются математические фигуры, но геометрически более простые (треугольники, прямоугольники, трапеции, рис. 37, а). В этом случае в масштабе карты измеряются элементы этих фигур (основания – a, высоты –b) и по простейшим формулам геометрии определяют их площади


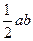

Площадь всего участка местности будет равна сумме площадей всех фигур, вписанных в данный криволинейный контур.
Точность этого способа зависит от масштаба карты, чем он крупнее, тем выше точность.
Анализируя графоаналитический способ определения площадей, не трудно заметить, что при использовании только одной геометрической фигуры для заполнения криволинейного контура способ становится универсальным и более оперативным. Действительно, построенная на прозрачной основе (целлулоид, стекло, плексиглас и т.п.), например, сетка квадратов (палетка) может использоваться для определения площадей извилистых контуров на любой карте или плане без каких-либо преобразований (см. рис.37,b)
a 


































 |
 |


|
 |
 |



площади участка местности
Рис. 37. Схема определения площади графоаналитическим способом:
а – геометрические фигуры, б – палетка
При использовании палетки её следует накладывать на контур сеткой вниз. Кроме того, для более точной оценки площадей дробных частей квадрата сетку строят таким образом: основные квадраты со стороной 1 см, а для оценки дробных частей дополнительные квадраты со стороной 2 мм.
Общая площадь участка в пределах данного контура будет равна числу полных сантиметровых квадратов. Затем числу целых мелких квадратов и, наконец, путём сложения расположенных на границе контура частей неполных мелких квадратов. Неполные квадраты оцениваются на глаз. Это самая трудоёмкая и наименее точная часть работы. Такой палеткой можно определять площади с ошибкой до 2%.
В некоторых случаях для определения площадей извилистых контуров целесообразно использовать механический способ.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Графоаналитическое определение площади
При определении площадей объектов недвижимости, имеющих границы прямолинейного очертания, используют формулы геометрии. Участок, исходя из его формы, разбивается на простые геометрические фигуры, такие как треугольники, прямоугольники, трапеции и другие. Формулы площадей геометрических фигур приведены в приложении А. При наличии значений измеренных углов поворота границы, можно использовать формулы тригонометрии (приложение Б).
Площадь объекта недвижимости разбивается на различные треугольники. В каждом из полученных треугольников измеряют основание а и высоту h при помощи циркуля-измерителя, и определяют по поперечному масштабу. Сумма отдельных площадей треугольников даст общую площадь землепользования. При наличии длин сторон полученных в процессе измерений на местности, предпочтение отдаётся им, а не измеренным на чертеже.
Для исключения грубых ошибок измерения нельзя использовать одни и те же основания для соседних треугольников. Исключению ошибок будет способствовать контрольное определение площадей тех же треугольников, но по другим измеренным основаниям и высотам.
Для определения площади небольших участков с криволинейными контурами применяют прямолинейные и криволинейные палетки.
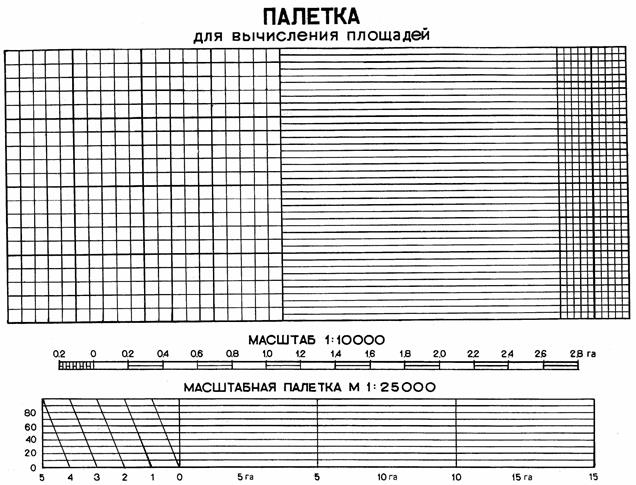
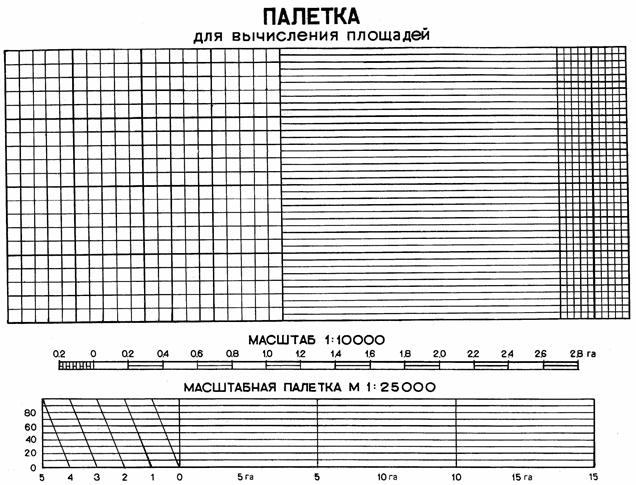
Прямолинейные палетки наиболее распространены. К ним относятся квадратные и параллельные палетки (рисунок 2).
Рисунок 2 – Прямолинейная палетка с масштабными номограммами площади
Квадратная палетка изготавливается на пластике со стороной квадратов 2–4 мм. Палетка накладывается на контур и подсчитывается число целых квадратов. Доли рассекаемых клеток учитываются на глаз. Зная размер клетки и масштаб карты, определяют площадь контура. Квадратной палеткой не рекомендуется определять площади более 2 см на плане. При использовании её возможны грубые ошибки.
Таблица 1 – Вычисление площади объекта недвижимости по координатам его вершин
| № съёмочной точки | Координата, м | Разность, м | Произведение, м 2 | ||
| Х | Y | Хк-1 – Хк+1 | Yк+1 – Yк-1 | Yк (Хк-1 – Хк+1) | Хк (Yк+1 – Yк-1) |
| 3 000.00 3 240.28 3 987.23 3 808.56 3 077.61 2 156.52 1 434.01 1 972.69 | 3 000.00 3 593.54 3 897.74 4 829.33 5 108.73 4 707.77 3 957.24 2 997.80 | –1 267.59 –987.23 568.28 +909.62 +1 652.04 +1 643.60 +183.83 –1 565.99 | +599.74 +897.74 +1 235.79 +1 210.99 –121.56 –1 151.49 –1 709.97 –957.24 | –3 802 770 –3 547 650 –2 215 008 +4 392 855 +8 439 826 +7 737 691 +7 274 459 –4 694 525 | +1 787 220 +2 908 929 +4 927 379 +4612 128 –374 114 –2 483 211 –2 452 114 –1 888 338 |
| 3 000.00 | 3 000.00 | Σ+ 4 389.09 Σ– 4 389.09 | Σ+ 3 940.26 Σ– 3 940.26 | Σ+ 21 297 831 Σ– 14 259 953 2S = 7 037 878 | Σ+ 14 235 656 Σ– 7 197 777 2S= 7 037 879 |
| S = 3 518 939 м 2 = 351.89 га |
Параллельная палетка не имеет недостатков квадратной. На пластик наносятся параллельные линии через 2 мм.
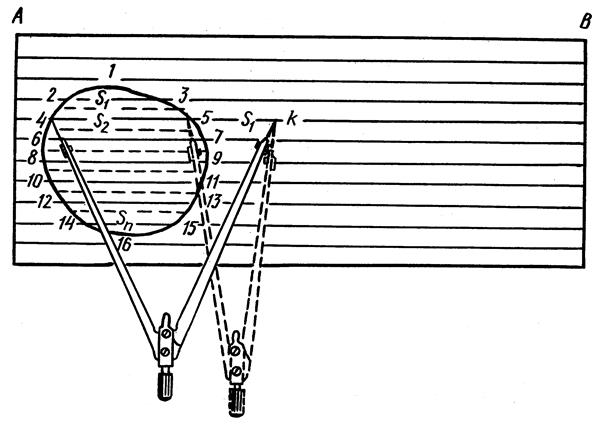
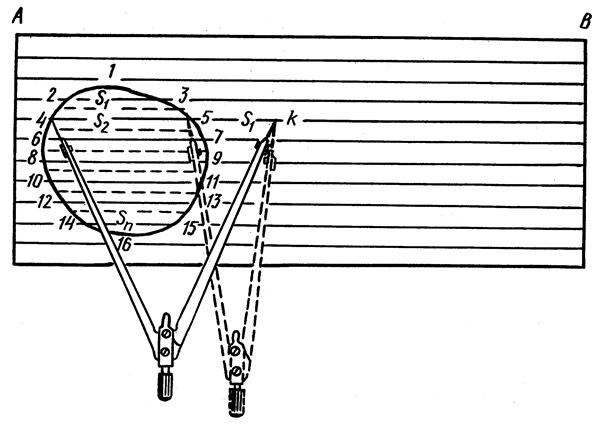
Порядок измерения параллельной палеткой следующий. Палетка накладывается на контур (рисунок 3) таким образом, чтобы две крайние точки (например, 1 и 16) разместились посередине между какими либо линиями палетки.
Рисунок 3 – Измерение параллельной палеткой
Соответственно, измеряемый контур делится линиями палетки на отдельные контуры по форме близкие к трапеции. Основания трапеций показаны воображаемыми пунктирными линиями, тогда средняя линия трапеции будет показана сплошной чёрной линией палетки. Высоты трапеций соответственно равны расстоянию между линиями палетки выраженному в метрах, с учётом масштаба.
Для определения площади контура определяют длину средних линий трапеций. В раствор циркуля-измерителя берётся отрезок S1, затем измеритель устанавливается справа на продолжении линии S2 в точки 5 и К. Левая ножка измерителя, при неподвижной правой, переносится в точку 4, и таким образом в растворе измерителя оказываются отрезки средних линий S1 и S2. Аналогичные действия выполняют вплоть до включения отрезка Sn заключённого между точками 14 и 15.
Затем по линейке поперечного масштаба определяется общая длина средних линий. Произведение суммы средних линий на высоту даст площадь контура в метрах квадратных. Которую при необходимости далее выражают в гектарах.
Если длины палетки АВ не хватает для измерения средних линий, то определение выполняется по частям.
На фабричной прямолинейной палетке (рисунок 2) имеется номограмма линейного и поперечного масштаба для определения площади контуров по сумме длин средних линий.
Параллельной палеткой не рекомендуется определять площади больше 10 см 2 на плане или карте.
Площадь протяжённого криволинейного объекта можно определить при помощи курвиметра (рисунок 4). Прокатывая курвиметр по оси контура, получают его длину в сантиметрах. Затем определяют длину с учётом масштаба. Ширину определяют графически по карте или берут из абриса. Площадь определяется как произведение длины на ширину.
Источник
Графоаналитическое определение площади



При определении площадей объектов недвижимости, имеющих границы прямолинейного очертания, используют формулы геометрии. Участок, исходя из его формы, разбивается на простые геометрические фигуры, такие как треугольники, прямоугольники, трапеции и другие. Формулы площадей геометрических фигур приведены в приложении А. При наличии значений измеренных углов поворота границы, можно использовать формулы тригонометрии (приложение Б).
Площадь объекта недвижимости разбивается на различные треугольники. В каждом из полученных треугольников измеряют основание а и высоту h при помощи циркуля-измерителя, и определяют по поперечному масштабу. Сумма отдельных площадей треугольников даст общую площадь землепользования. При наличии длин сторон полученных в процессе измерений на местности, предпочтение отдаётся им, а не измеренным на чертеже.
Для исключения грубых ошибок измерения нельзя использовать одни и те же основания для соседних треугольников. Исключению ошибок будет способствовать контрольное определение площадей тех же треугольников, но по другим измеренным основаниям и высотам.
Для определения площади небольших участков с криволинейными контурами применяют прямолинейные и криволинейные палетки.
Прямолинейные палетки наиболее распространены. К ним относятся квадратные и параллельные палетки (рисунок 2).
Рисунок 2 – Прямолинейная палетка с масштабными номограммами площади
Квадратная палетка изготавливается на пластике со стороной квадратов 2–4 мм. Палетка накладывается на контур и подсчитывается число целых квадратов. Доли рассекаемых клеток учитываются на глаз. Зная размер клетки и масштаб карты, определяют площадь контура. Квадратной палеткой не рекомендуется определять площади более 2 см на плане. При использовании её возможны грубые ошибки.
Таблица 1 – Вычисление площади объекта недвижимости по координатам его вершин
| № съёмочной точки | Координата, м | Разность, м | Произведение, м 2 | ||
| Х | Y | Хк-1 – Хк+1 | Yк+1 – Yк-1 | Yк (Хк-1 – Хк+1) | Хк (Yк+1 – Yк-1) |
| 3 000.00 3 240.28 3 987.23 3 808.56 3 077.61 2 156.52 1 434.01 1 972.69 | 3 000.00 3 593.54 3 897.74 4 829.33 5 108.73 4 707.77 3 957.24 2 997.80 | –1 267.59 –987.23 568.28 +909.62 +1 652.04 +1 643.60 +183.83 –1 565.99 | +599.74 +897.74 +1 235.79 +1 210.99 –121.56 –1 151.49 –1 709.97 –957.24 | –3 802 770 –3 547 650 –2 215 008 +4 392 855 +8 439 826 +7 737 691 +7 274 459 –4 694 525 | +1 787 220 +2 908 929 +4 927 379 +4612 128 –374 114 –2 483 211 –2 452 114 –1 888 338 |
| 3 000.00 | 3 000.00 | Σ+ 4 389.09 Σ– 4 389.09 | Σ+ 3 940.26 Σ– 3 940.26 | Σ+ 21 297 831 Σ– 14 259 953 2S = 7 037 878 | Σ+ 14 235 656 Σ– 7 197 777 2S= 7 037 879 |
| S = 3 518 939 м 2 = 351.89 га |
Параллельная палетка не имеет недостатков квадратной. На пластик наносятся параллельные линии через 2 мм.
Порядок измерения параллельной палеткой следующий. Палетка накладывается на контур (рисунок 3) таким образом, чтобы две крайние точки (например, 1 и 16) разместились посередине между какими либо линиями палетки.
Рисунок 3 – Измерение параллельной палеткой
Соответственно, измеряемый контур делится линиями палетки на отдельные контуры по форме близкие к трапеции. Основания трапеций показаны воображаемыми пунктирными линиями, тогда средняя линия трапеции будет показана сплошной чёрной линией палетки. Высоты трапеций соответственно равны расстоянию между линиями палетки выраженному в метрах, с учётом масштаба.
Для определения площади контура определяют длину средних линий трапеций. В раствор циркуля-измерителя берётся отрезок S1, затем измеритель устанавливается справа на продолжении линии S2 в точки 5 и К. Левая ножка измерителя, при неподвижной правой, переносится в точку 4, и таким образом в растворе измерителя оказываются отрезки средних линий S1 и S2. Аналогичные действия выполняют вплоть до включения отрезка Sn заключённого между точками 14 и 15.
Затем по линейке поперечного масштаба определяется общая длина средних линий. Произведение суммы средних линий на высоту даст площадь контура в метрах квадратных. Которую при необходимости далее выражают в гектарах.
Если длины палетки АВ не хватает для измерения средних линий, то определение выполняется по частям.
На фабричной прямолинейной палетке (рисунок 2) имеется номограмма линейного и поперечного масштаба для определения площади контуров по сумме длин средних линий.

Параллельной палеткой не рекомендуется определять площади больше 10 см 2 на плане или карте.
Площадь протяжённого криволинейного объекта можно определить при помощи курвиметра (рисунок 4). Прокатывая курвиметр по оси контура, получают его длину в сантиметрах. Затем определяют длину с учётом масштаба. Ширину определяют графически по карте или берут из абриса. Площадь определяется как произведение длины на ширину.
Источник