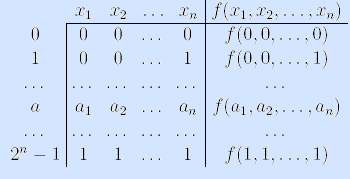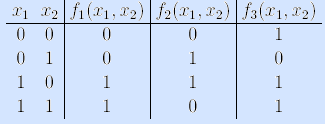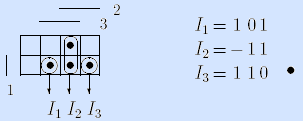Графический способ задания булевой функции осуществляется с помощью

IX Международная студенческая научная конференция Студенческий научный форум — 2017

СПОСОБЫ ЗАДАНИЯ БУЛЕВЫХ ФУНКЦИЙ

Переменная x называется булевой, если она способна принимать только два значения 0 и 1. В качестве примера интерпретации такого рода переменных может выступать обычный настенный выключатель света на два положения. Здесь 1 соответствует положению переключателя вверх и 0 — положению вниз.

Способы задания булевых функций не отличаются от способов задания обычных функций анализа. К таковым способам задания стандартно относятся: табличный; графический; аналитический.

Графический способ задания

Рассмотрим графическое представление булевой функции трех аргументов w=f(x,y,z). Заметим, что множество наборов области определения функции D=<(x,y,z) | x,y,z ∈ <0,1>> является множеством координат точек вершин единичного трехмерного куба (рис. 1). Очевидный способ графического представления булевой функции — это отметить каким-то образом вершины куба, в которых функция принимает значение 1. Именно так на рис. 1 и сделано. В соответствии с областью определения функции D отмечены вершины, в которых булева функция равна 1.

Аналитический способ задания.

Функции 0 и 1 называются соответственно тождественным нулем и тождественной единицей. Иногда эти функции 0 и 1 рассматривают как функции, зависящие от пустого множества переменных. Функции одного и двух аргументов называются элементарными.

, участвующие в обозначениях элементарных функций, называются логическими связками (операциями) или функциональными символами.

На практике очень часто приходится реализовывать совокупности булевых функций. Если произвести минимизацию булевых функций, входящих в систему, независимо друг от друга, то общая схема будет состоять из изолированных подсхем. Ее можно иногда упростить за счет объединения участков подсхем, реализующих одинаковые члены, входящие в несколько булевых функций системы.

Задача минимизации систем булевых функций хорошо исследована в классе функционально полных систем: «дизъюнкция», «конъюнкция», «отрицание». В ряде случаев, преобразования над формулами булевых функций удобно производить в алгебре Жегалкина. Алгебра Жегалкина включает две двухместные операции: конъюнкцию и сложение, а также константу 1. Здесь имеют место те же законы:

х + y = y + х, х у = у х (закон коммутативности);

х + (у + z) = (х + у) + z, х(у z) = (х у)z (закон ассоциативности);

x (y + z) = x y + x z (закон дистрибутивности).

Из коммутативности и ассоциативности дизъюнкции следует, что дизъюнкция нескольких переменных может выполняться последовательно, причем порядок взятия дизъюнкции не влияет на результат.

Хабарова, В.В. Модель движения корнеплодов в процессе резания консольными ножами// Материалы Международной научно-практической конференции «Актуальные вопросы аграрной науки и образования», Ульяновск: Ульяновская ГСХА, 2010, т.III, ч.3, с. 129-133

Хабарова, Виктория Валерьевна. Разработка измельчителя корнеплодов с обоснованием его параметров и режимов работы: автореферат дис. … канд. технич. наук / Хабарова В.В. – Уфа, 2011.- 20 с.

Исаев Ю.М., Хабарова В.В., Богатов В.А. Процесс измельчения корнеплодов консольными ножами. – Механизация и электрификация сельского хозяйства, 2008, № 1, с. 14 – 16.

Хабарова, В.В. Математическое обоснование процесса деформации при измельчении корнеплодов/В.В. Хабарова, В.И. Ермолаева// Аграрная наука и образование на современном этапе развития: опыт, проблемы и пути их решения. Материалы VI Международной научно-практической конференции.- Ульяновская ГСХА, 2015. С. 118-119.

Хабарова, В.В. Анализ факторов, определяющих энергозатраты с вибрациями при измельчении корнеплодов и бахчевых/ В.В. Хабарова, В.А. Богатов, Е.И. Зотов // Вестник Ульяновской государственной сельскохозяйственной академии. — № 1 (2) январь — март 2006 г. — C. 67-70.

Хабарова, Виктория Валерьевна. Определение оптимальной частоты вибрации ножей при измельчении корнеплодов/В.В. Хабарова// Материалы IV Международной научно-практической конференции «Аграрная наука и образование на современном этапе развития: опыт, проблемы и пути их решения» 22-24 ноября Ульяновская государственная сельскохозяйственная академия. – Ульяновск, 2012.

Хабарова, В.В. К вопросу обоснования конструктивных особенностей измельчителя корнеплодов / В.В. Хабарова, В.И. Ермолаева// Материалы VI Международной научно-практической конференции «Аграрная наука и образование на современном этапе развития: опыт, проблемы и пути их решения». — Ульяновск: ГСХА, 2015. С. 197-199.

Хабарова, Виктория Валерьевна. Разработка измельчителя корнеплодов с обоснованием его параметров и режимов работы/ Диссертация на соискание ученой степени кандидата технических наук / Башкирский государственный аграрный университет. Уфа, 2011.

Источник

Графический способ задания булевой функции осуществляется с помощью

1) Задание булевой функции таблицей истинности. Так называется таблица, состоящая из двух частей: в левой части перечисляются все наборы значений аргументов (булевы векторы пространства B n ) в естественном порядке, то есть по возрастанию значений чисел, представляемых этими векторами, а в правой части – значения булевой функции на соответствующих наборах.

Пример. Рассмотрим булеву функцию трех аргументов, называемую мажоритарной (или функцией голосования): она принимает значение 1 на тех и только тех наборах, в которых единиц больше, чем нулей (major – больший).

Так как левая часть таблицы истинности постоянна для всех функций с одинаковым числом аргументов, несколько таких функций могут быть заданы общей таблицей.

Теорема о числе булевых функций. Число различных булевых функций, зависящих от n переменных, равно 2 2 n .

Доказательство. Каждая булева функция определяется своим столбцом значений. Столбец является булевым вектором длины m=2 n , где n – число аргументов функции. Число различных векторов длины m (а значит и число булевых функций, зависящих от n переменных) равно 2 m =2 2 n . •

2) Задание булевой функции характеристическими множествами. Так называются два множества:

M 1 _f, состоящее из всех наборов, на которых функция принимает значение 1, то есть M 1 _f = <α B n :f(α) = 1>;

M 0 _f, состоящее из всех наборов, на которых функция принимает значение 0, то есть M 0 _f = <α B n :f(α) = 0>.

Пример (мажоритарная функция).

3) Задание булевой функции вектором ее значений.

Пример (мажоритарная функция).

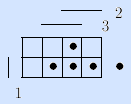
4) Задание булевой функции матрицей Грея. Булево пространство задается матрицей Грея, и наборы (клетки матрицы), на которых булева функция f(x₁, …, x_n) принимает значение 1, отмечаются и называются точками.

Пример (мажоритарная функция).

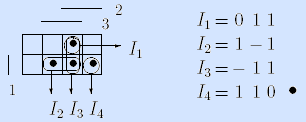
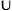
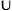
5) Интервальный способ задания булевой функции. Булеву функцию f(x₁, …, x_n) можно задать множеством интервалов I_f = 1, I₂, …, I_k>, объединение которых образует характеристическое множество M 1 _f, то есть I₁ I₂… I_k = M 1 _f. Множество интервалов I_f называется достаточным для функции f(x₁, …, x_n).

Пример. Мажоритарная функция может быть задана достаточным множеством I_f = 1, I₂, I₃> интервалов:

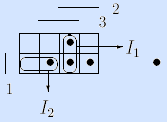
Здесь интервалы представлены троичными векторами и изображены на матрице Грея.

В отличие от предыдущих, интервальный способ задания функций многовариантен (одну и ту же булеву функцию можно представить разными множествами интервалов).

Пример. Зададим мажоритарную функцию другим достаточным множеством I’_f = 1, I₂, I₃, I₄> интервалов:

Очевидно, что это множество интервалов избыточно: первый интервал (011) можно удалить.

Определение. Интервал назовем допустимым для булевой функции, если на всех его наборах функция равна 1.

Примеры. I₁= – 1 1 – допустимый интервал для мажоритарной функции, I₂= 1 0 – – не допустимый.

Определение. Интервал I назовем максимальным для булевой функции f(x₁, …, x_n), если он является допустимым для этой функции, и не существует другого допустимого интервала I’, такого что I 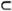I’.

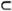
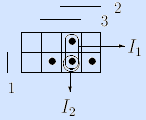
Пример. I₁= –11 является максимальным интервалом для мажоритарной функции, а допустимый интервал I₂ = 111 не является максимальным, так как I₂ I₁.

Пример. Зададим мажоритарную функцию множеством I»_f = 1 I₂, I₃> всех максимальных интервалов.

Определение. Точку булевой функции f(x₁, …, x_n) назовем ядерной, если она принадлежит ровно одному максимальному для этой функции интервалу. Максимальный интервал называется ядерным, если он содержит ядерную точку.

Пример. Для мажоритарной функции ядерными точками являются 011 (принадлежит только интервалу –11), 101 (принадлежит только интервалу 1 –1) и 110 (принадлежит только интервалу 11 –). Все максимальные интервалы этой функции являются ядерными. •

Очевидно, что все ядерные интервалы входят в любое достаточное множество функции, состоящее из максимальных интервалов.

6) Задание булевой функции формулами будет рассмотрено несколько позже.

Источник

Графический способ задания булевой функции осуществляется с помощью

Определение. Переменная x называется булевой, если она способна принимать только два значения 0 и 1. В качестве примера интерпретации такого рода переменных может выступать обычный настенный выключатель света на два положения. Здесь 1 соответствует положению переключателя вверх и 0 — положению вниз.
Определение. Функция f(x 1,x 2,…,x n) называется булевой (или логической, или функцией алгебры логики, или переключательной), если все ее аргументы x[i] являются булевыми, а сама функция также может принимать только два значения 0 и 1. Множество всех булевых функций от переменных x 1,x 2,…,x n обозначают через P 2.

Способы задания булевых функций

Способы задания булевых функций не отличаются от способов задания обычных функций анализа. К таковым способам задания стандартно относятся:
1) табличный;
2) графический;
3) аналитический.

(1) Табличный способ задания

Пусть w=f(x 1,x 2,…,x n) — булева функция n аргументов. Область определения данной функции можно рассматривать и как множество упорядоченных наборов (или векторов, или двоичных наборов) D=,x 2,…,x n | x i ∈ <0,1>, i=1,2,…,n>, на каждом из которых функция принимает одно из двух значений: w ∈ <0,1>. Количество таких наборов (x 1,x 2,…,x n), согласно правилу прямого произведения, равно |D|=

В качестве примера рассмотрим табличное представление булевой функции трех аргументов w=f(x,y,z), где w,x,y,z ∈ <0,1>. Область определения функции — это множество двоичных наборов D=<(x,y,z), | x,y,z ∈ <0,1>>. Их число есть |D|=2^3=8, а количество таких функций равно 2^|D|=2^2^3=256. Значения функции f(x,y,z) удобно представить в виде табл. 1.3, где перечислены всевозможные наборы из нулей и единиц длины 3 и для каждогонабора указано значение функции f i ∈ <0,1>на этом наборе.

В таблицах, аналогичных табл. 1.3 обычно употребляется расположение наборов, соответствующих порядку естественного роста двоичных чисел 0,1,…2^n-1, в
примере n=3.
Определение. Таблицы значений булевых функций, подобные табл. 1.3, называются таблицами истинности булевых функций. Название таблиц происходит от интерпретации значений 1 — истина (TRUE), 0 — ложь (FALSE).

(2) Графический способ задания

Рассмотрим графическое представление булевой функции трех аргументов w=f(x,y,z), заданной таблично (табл. 1.3). Заметим, что множество наборов области определения функции D=<(x,y,z) , | x,y,z ∈ <0,1>> является множеством координат точек вершин единичного трехмерного куба (рис. 1.2). Очевидный способ графического представления булевой функции — это отметить каким-то образом вершины куба, в которых функция принимает значение 1. Именно так на рис. 1.2 и сделано. В соответствии с таблицей значений (табл. 1.3) отмечены вершины, в которых булева функция равна 1.

Замечание. Очевидно, что область определения булевой функции n аргументов w=f(x 1,x 2,…,x n) составляется из наборов координат точек вершин единичного n-мерного куба.

(3) Аналитический способ задания

Приведем таблицы истинности, обозначения и названия булевых функций одного и двух аргументов. В табл. 1.4 представлены все (их 2^2^1=4) функции одного аргумента, в табл. 1.5 — все функции двух аргументов (их 2^2^2=16).

x	0 1	Обозначение	Название
0	0 0	0	Нуль, const 0
1	0 1	x	Повторение x
2	1 0	¬x, x	Отрицание x, не x
3	1 1	1	Единица, const 1

Функции 0 и 1 называются соответственно тождественным нулем и тождественной единицей. Иногда эти функции 0 и 1 рассматривают как функции, зависящие от пустого множества переменных.

x у	0 0 1 1 0 1 0 1	Обозначение	Название
0	0 0 0 0	0	Нуль, const 0
1	0 0 0 1	x•y,x∧y,x&y	Конъюнкция
2	0 0 1 0	yx,x• y	Запрет по x
3	0 0 1 1	x	Повторение x
4	0 1 0 0	x, x •y	Запрет по y
5	0 1 0 1	y	Повторение y
6	0 1 1 0	x⊕y	Сумма по модулю 2
7	0 1 1 1	x∨y	Дизъюнкция
8	1 0 0 0	x↓y	Стрелка Пирса
9	1 0 0 1	x y	Эквивалентность
10	1 0 1 0	¬y, y	Отрицание y
11	1 0 1 1	y→x, y⇒x, y⊃x	Импликация от y к x
12	1 1 0 0	¬x, x	Отрицание x
13	1 1 0 1	x→y, x⇒y, x⊃y	Импликация от x к y
14	1 1 1 0	x|y	Штрих Шеффера
15	1 1 1 1	1	Единица, const 1

Функции одного и двух аргументов, представленные в таблицах 1.4 и 1.5, называются элементарными.

, участвующие в обозначениях элементарных функций, называются логическими связками (операциями) или функциональными символами.

Источник