Графический способ умножения чисел что это

Графический способ умножения

Данная презентация расчитана на защиту учебного проекта по математике «Графический способ умножения»

Просмотр содержимого документа
«Графический способ умножения»

Выполнила: Снопок Дарья

ученица 5 класса

МАОУ НГО «СОШ № 12»

Руководитель: Жвакина Анастасия Михайловна

учитель МАОУ НГО «СОШ № 12»

• Изучить графический способ умножения чисел и его применение при вычислениях числовых выражений.

• Разобрать данный способ умножения.
• Рассказать о новом способе умножения и научить им пользоваться других.
• Развить навыки графического способа умножения.

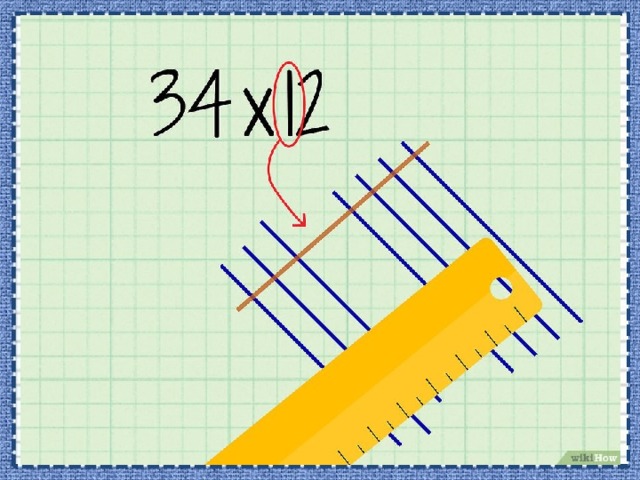
• Определите разряды цифр первого числа. Нужно определить количество разрядов и разряды каждой цифры.

• Например, нужно перемножить . У числа 34 цифра 4 стоит в разряде единиц, а цифра 3 – в разряде десятков.

• Нарисуйте параллельные линии, представляющие разряд десятков первого числа. Количество линий соответствует цифре, которая стоит в разряде десятков.

• Нарисуйте наклонные линии (под углом в 45 градусов), которые убывают слева направо.

• Например, в случае числа 34 нарисуйте 3 параллельные линии.

• Нарисуйте параллельные линии, представляющие разряд единиц первого числа. Количество линий соответствует цифре, которая стоит в разряде единиц. Эти линии нарисуйте справа и выше линий, представляющих разряд десятков.

• Между линиями разряда десятков и линиями разряда единиц оставьте пустое пространство, чтобы отличать их.

• Например, в случае числа 34 нарисуйте 4 параллельные линии.

• Определите разряды цифр второго числа. Нужно определить количество разрядов и разряды каждой цифры.
• • В нашем примере у числа 12 цифра 2 стоит в разряде единиц, а цифра 1 – в разряде десятков.

• Нарисуйте параллельные линии, представляющие разряд десятков второго числа. Количество линий соответствует цифре, которая стоит в разряде десятков. Линии проведите в верхней части линий первого числа. Линии второго числа должны пересекать линии первого числа и возрастать справа налево.
• • Лучше нарисовать линии первого и второго чисел разными цветами.

• Например, в случае числа 12 нарисуйте 1 линию.

• Нарисуйте параллельные линии, представляющие разряд единиц второго числа. Количество линий соответствует цифре, которая стоит в разряде единиц. Эти линии нарисуйте справа и ниже линий, представляющих разряд десятков. Линии второго числа должны пересекать линии первого числа и возрастать справа налево.
• Между линиями разряда десятков и линиями разряда единиц оставьте пустое пространство, чтобы отличать их.
• Например, в случае числа 12 нарисуйте 2 параллельные линии.

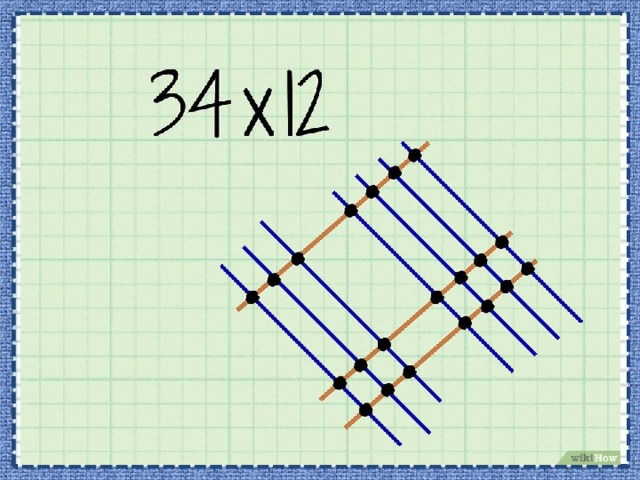
• Отметьте точки пересечений линий. Графический способ умножения подразумевает сложение точек, а не умножение чего-либо.

• Обведите точки, представляющие разряд единиц. Это точки пересечения линий разряда единиц первого и второго чисел.
• Вспомните, что 1 умножить на 1 равно 1.
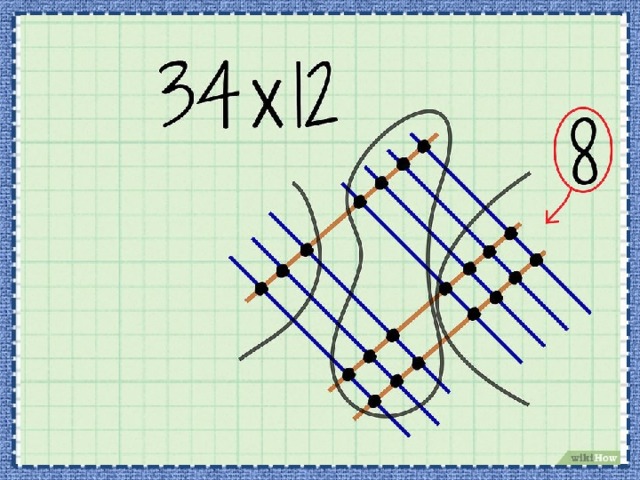
• В нашем примере ( обведите точки пересечения четырех линий с двумя линиями (правая часть рисунка).

• Обведите точки, представляющие разряд десятков. Это точки пересечения линий разряда десятков (первого или второго числа) с линиями разряда единиц (первого или второго числа).
• Вспомните, что 1 умножить на 10 равно 10.
• В нашем примере обведите точки пересечения одной линии с четырьмя линиями (верхняя часть рисунка) и точки пересечения двух линий с тремя линиями (нижняя часть рисунка).

• Обведите точки, представляющие разряд сотен. Это точки пересечения линий разряда десятков первого и второго чисел.
• Вспомните, что 10 умножить на 10 равно 100.
• В нашем примере обведите точки пересечения трех линий с одной линией (левая часть рисунка).

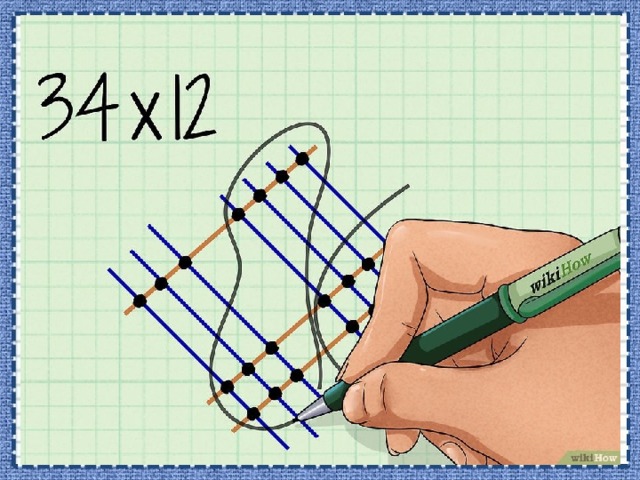
• Сложите точки разряда единиц. Эти точки обведены в правой части рисунка. Полученную цифру запишите в разряд единиц конечного ответа.
• В нашем примере вы насчитаете 8 точек разряда единиц. Таким образом, 8 – это цифра, которая будет стоять в разряде единиц конечного числа.

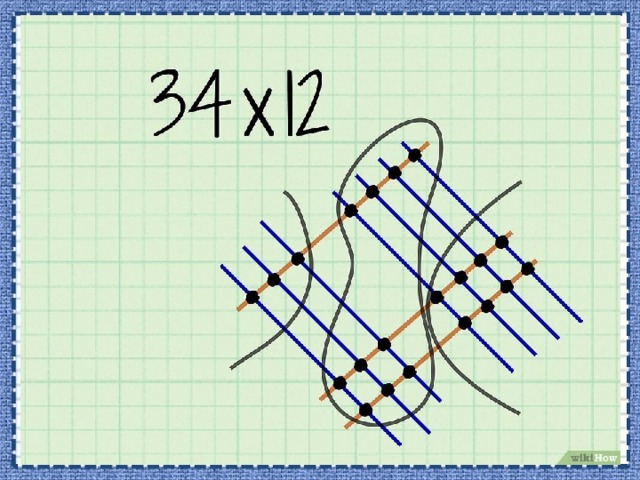
• Сложите точки разряда десятков. Эти точки обведены в верхней и нижней частях рисунка. Полученную цифру запишите в разряд десятков конечного ответа.
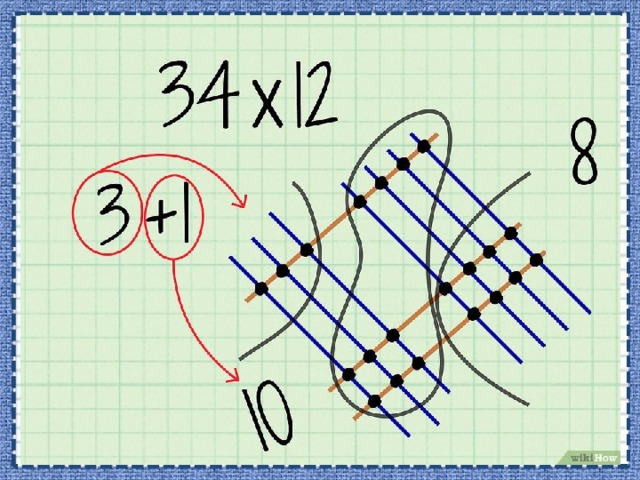
• В нашем примере вы насчитаете 10 точек разряда десятков.
• Вспомните, что если в операции сложения или умножения получилось двузначное число, применяется перенос цифр. Вы насчитали 10 точек; таким образом, 0 запишите в разряд десятков, а 1 перенесите в разряд сотен (конечного числа).

• Сложите точки разряда сотен. Эти точки обведены в левой части рисунка. Полученную цифру запишите в разряд сотен конечного ответа.
• В нашем примере вы насчитаете 3 точки разряда сотен.
• Не забудьте прибавить перенесенную цифру. В нашем примере из разряда десятков в разряд сотен перенесли 1, поэтому 3+1=4. Таким образом, запишите 4 в разряд сотен конечного числа.

• Запишите окончательный ответ. Запишите цифры (рядом друг с другом), найденные для каждого разряда.
• В нашем примере вы нашли, что цифра 8 должна стоять в разряде единиц, цифра 0 – в разряде десятков, цифра 4 – в разряде сотен. Таким образом, окончательный ответ: 408.

Источник

Графический способ умножения чисел

Муниципальное бюджетное общеобразовательное учреждение » Средняя школа № 23 города Димитровграда Ульяновской области»

Графический способ умножения

Подготовил: Клоков Вадим

Ученик 5 класс А

Руководитель проекта: Иванова А.Л.

Учитель первой категории

Димитровград, 2019 год

Мне задали подготовить проект на тему «Графический способ умножения чисел».

В истории математики известно около 30 способов умножения. Метод умножения в столбик один из них. Но есть ещё более интересный и доступный способ.

Предложенный метод позволяет перемножать любые многозначные числа. Этот метод прост для понимания, не требует знаний таблицы умножения, нужна только внимательность.

Суть метода: многозначное число изображается с помощью линий, причем различные разряды этого числа имеют разный цвет.

Происхождение графического способа умножения неизвестно – утверждают, что его придумали японцы, китайцы или арии. В основе этого метода лежит стандартный способ перемножения чисел, но он представлен в наглядной (графической) форме. Используйте пересечения линий, чтобы перемножать разные разряды чисел; этот метод подойдет визуально ориентированным учащимся.

Графические вычисления – методы получения численных решений различных задач путём графических построений. Графические вычисления представляют систему построений, повторяющих или заменяющих с известным приближением соответствующие аналитические операции. Графическое выполнение этих операций требует каждый раз последовательности построений, приводящих в результате к графическому определению искомой величины. Достоинства графического вычисления — простота их выполнения и наглядность. Недостаток — малая точность получаемых ответов. Но в нашем случае графический способ умножения многозначных чисел очень удобен , так как и наглядно и ответ точный.

УМНОЖЕНИЕ ДВУЗНАЧНЫХ ЧИСЕЛ

Рассмотрим произведение чисел 31 и 12. Заранее условимся десятки изображать линиями красного цвета, а единицы – синего. Число 31 это 3 десятка и 1 единица. Изобразим горизонтально 3 линии красного цвета и одну синего. Число 12 это 1 десяток и 2 единицы, изобразим вертикально 1 линию красного и 2 синего цвета. Теперь считаем точки пересечения:

1) красные линии дают 3 точки – это разряд сотен (первая цифра произведение);

2) пересечение красных и синих линий (7 точек) – это разряд десятков (вторая цифра произведение);

3) пересечения синих линий (2 точки) – это разряд единиц (третья цифра произведения).

Таким образом, в ответе получилось число 372.

Если при подсчёте точек их количество больше 10, то единицу отдают предыдущему разряду.

Например, 64 · 53 (рис. 1)

Количество пересечения красных линий – 30, синие и красные пересекаются в 38 точках, значит к цифре 0 числа 30 прибавляем цифру 3 числа 38, получаем 338. Количество точек пересечения синих линий равно 12, значит к цифре 8 прибавляем 1, получаем 3392.

УМНОЖЕНИЕ ТРЕХЗНАЧНОГО ЧИСЛА НА ДВУЗНАЧНОЕ И НА ТРЕХЗНАЧНОЕ

Трехзначные числа имеют разряд сотен, десятков, единиц. Разряд сотен будем изображать линиями зеленного цвета. Выполняем построение по такому же принципу. Умножим 321 на 42

321: 3 сотни, 2 десятка, 1 единицы, а значит 3 линии зеленного цвета, 2 – красного, 1 – синего.

42: 4 десятка, 2 единицы. 4 линии красного цвета, 2 – синего. Проведем дуги так, как показано на рисунке. В первой группе 12 точек, во второй 14, получаем 134. Третью группу составляют 8 точек – 1348, и последняя четвертая группа содержит 2 точки. Итог: 13482.

Источник

Проект по теме: «Графический способ умножения»

Выбранный для просмотра документ Графический способ умножения.docx

Управление образования городского округа «Охинский»

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа № 1 г. Охи

Математика и информатика

ТЕМА ПРОЕКТНОЙ РАБОТЫ

Составитель: Ишин Денис Михайлович

Научный руководитель: Кравчук Мария Аркадьевна,

учитель математики МБОУ СОШ №1 г.Охи

Глава 1. УМНОЖЕНИЕ ДВУЗНАЧНЫХ ЧИСЕЛ ……………………………

Глава 2. УМНОЖЕНИЕ ТРЕХЗНАЧНОГО ЧИСЛА НА ДВУЗНАЧНОЕ И НА ТРЕХЗНАЧНОЕ …………………………………………………………….

В последнее время ребята всё с большей неохотой относятся к учёбе, и в частности к математике. Многие ученики не знают даже таблицы умножения! Чтобы привлечь внимание учащихся к математике и ответить на вопрос «Надо ли знать таблицу умножения?» я выбрал тему своего проекта «Графический способ умножения чисел».

В ходе анкетирования ( Приложение 1 ) своего класса, выяснилось, что таблицу умножения на отметку «5» и «4» знают 56% моих одноклассников, на «3» — 34%, «2» — 10%. При этом 95% считают, что современному человеку просто необходимо уметь считать. Но другого способа кроме умножения в столбик большинство не знают и хотели бы узнать. Приложение 2

Цель: ознакомление с графическим способом умножения многозначных чисел, и его применение при вычислениях.

Найти и разобрать графический способ умножения.

Рассказать об этом способе умножения и научить одноклассников применять новый способ умножения.

Актуальность: привлечь внимание учащихся к математике, помочь тем кто плохо знает таблицу умножения.

В истории математики известно около 30 способов умножения. Метод умножения в столбик один из них. Но есть ещё более интересный и доступный способ.

Предложенный метод позволяет перемножать любые многозначные числа. Этот метод прост для понимания, не требует знаний таблицы умножения, нужна только внимательность.

Суть метода: многозначное число изображается с помощью линий, причем различные разряды этого числа имеют разный цвет.

Глава 1. УМНОЖЕНИЕ ДВУЗНАЧНЫХ ЧИСЕЛ

Рассмотрим произведение чисел 31 и 12. Заранее условимся десятки изображать линиями красного цвета, а единицы – синего. Число 31 это 3 десятка и 1 единица. Изобразим горизонтально 3 линии красного цвета и одну синего. Число 12 это 1 десяток и 2 единицы, изобразим вертикально 1 линию красного и 2 синего цвета (рис. 1)

Теперь считаем точки пересечения:

1) красные линии дают 3 точки – это разряд сотен (первая цифра произведение);

2) пересечение красных и синих линий (7 точек) – это разряд десятков (вторая цифра произведение);

3) пересечения синих линий (2 точки) – это разряд единиц (третья цифра произведения).

Таким образом, в ответе получилось число 372.

Если при подсчёте точек их количество больше 10, то единицу отдают предыдущему разряду.

Например, 64 · 53 (рис. 2)

Количество пересечения красных линий – 30, синие и красные пересекаются в 38 точках, значит к цифре 0 числа 30 прибавляем цифру 3 числа 38, получаем 338. Количество точек пересечения синих линий равно 12, значит к цифре 8 прибавляем 1, получаем 3392.

Глава 2. УМНОЖЕНИЕ ТРЕХЗНАЧНОГО ЧИСЛА НА ДВУЗНАЧНОЕ И НА ТРЕХЗНАЧНОЕ

Трехзначные числа имеют разряд сотен, десятков, единиц. Разряд сотен будем изображать линиями зеленного цвета. Выполняем построение по такому же принципу. Умножим 321 на 42 (рис. 3)

321: 3 сотни, 2 десятка, 1 единицы, а значит 3 линии зеленного цвета, 2 – красного, 1 – синего.

42: 4 десятка, 2 единицы. 4 линии красного цвета, 2 – синего. Проведем дуги так, как показано на рисунке. В первой группе 12 точек, во второй 14, получаем 134. Третью группу составляют 8 точек – 1348, и последняя четвертая группа содержит 2 точки. Итог: 13482.

312: 3 сотни,1 десяток, 2 единицы

143: 1 сотня, 4 десятка, 3 единицы

1 группа – 3 точки (3)

2 группа – 13 точек ((3+1) 3 = 43

3 группа – 15 точек (4 (3+ 1) 5 = 445)

4 группа – 11 точек (44 (5 + 1) 1 = 4461)

5 группа – 6 точек (44616)

Графический способ умножения очень понравился моим одноклассникам и учащимся других классов. На вопрос: «Будут ли они использовать его при выполнении умножения?» большинство ребят ответили – «да».

Узнав этот способ, ребёнок уже в 1-ом классе сможет перемножать любые числа на листе бумаги, при этом процесс будет намного интересней, чем старый способ умножения «столбиком».

Возможно, что первого раза у многих не получится быстро, с ходу, выполнять эти подсчёты. Не беда. Нужна постоянная вычислительная тренировка. Она поможет приобрести полезные навыки счёта!

Источник