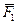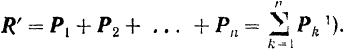Графический способ сложения сил
Система сходящихся сил на плоскости и в пространстве
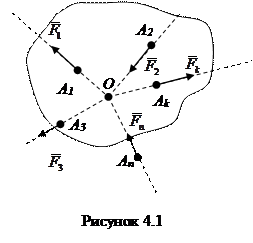
Система сил, линии, действия которых пересекаются одной точке, называется системой сходящихся сил (рисунок 4.1).
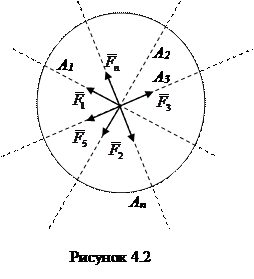
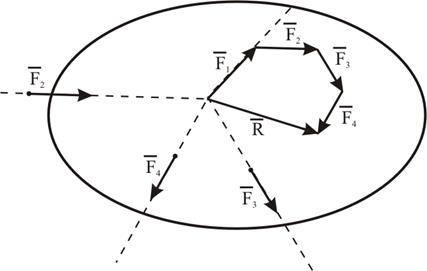
Так как силы можно переносить по линии их действия, то эту систему сил всегда можно заменить системой сил, приложенных к одной точке (рисунок 4.2).
Рассмотрим два способа сложения сходящихся сил: графический и аналитический.
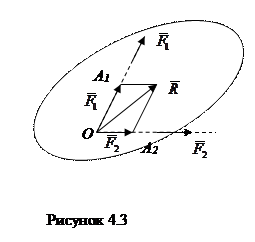
Равнодействующая двух сил, приложенных к одной точке, находится согласно аксиоме параллелограмма сил как диагональ параллелограмма, построенного на этих силах (рисунок 4.3), или как замыкающая сторона силового треугольника (рисунок 4.4). Следовательно, равнодействующая двух сил равна их геометрической сумме:
|
(4.1)
|
|
|
|
|
|
|
|
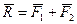
Найдем равнодействующую системы сходящихся сил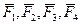 
. Будем складывать их последовательно по правилу силового треугольника (Рисунок 4.4).
Чтобы найти равнодействующую системы сходящихся сил графическим способом, надо построить в точке пересечения их действия силовой многоугольник на слагаемых силах, т.е. к концу вектора первой силы приложить вектор, геометрически равный второй силе и т.д.
Вектор, соединяющий начало первого слагаемого вектора с концом последнего, т.е. замыкающая сторона силового многоугольника, является равнодействующей системы сходящихся сил.
(4.2)
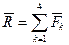
Величину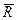 
, равную геометрической сумме сил какой-нибудь системы, будем в дальнейшем называть главным вектором этой системы.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
ПроСопромат.ру
Технический портал, посвященный Сопромату и истории его создания
Геометрический (графический) метод сложения сил, приложенных в одной точке
Силы называют сходящимися, если их линии действия пересекаются в одной точке.
Различают плоскую систему сходящихся сил, когда линии действия всех данных сил лежат в одной плоскости, и пространственную систему сходящихся сил, когда линии действия сил лежат в разных плоскостях.
На основании следствия из третьей аксиомы, силу можно переносить по линии ее действия. Поэтому сходящиеся силы всегда можно перенести в одну точку, а именно, в точку пересечения их линий действия.
Рассмотрим плоскую систему сходящихся сил. На рис. а приведена такая система сил, линии действия которых пересекаются в точке К.
Пользуясь указанным следствием из третьей аксиомы, перенесем все силы в точку К. Такой перенос необходим для графического определения равнодействующей заданной системы сил.
Выполнив этот перенос, получим четыре силы Р1 , Р2 , Р3 и Р4 , приложенные в точке К. Для определения их равнодействующей сложим последовательно все данные силы, используя правило треугольника (рис.б).
Сложим сначала две силы Р1 и Р2. Из произвольной точки О проведем, сохраняя масштаб и направление, силу Р1. Из конца силы Р1 проведем вторую силу Р2. Соединив точку О с концом силы Р2, получим силу R1, равную сумме сил Р1 и Р2,
Из конца силы R1 проведем третью силу Р3. Соединив точку О с концом силы Р3, получим силу R2, равную сумме сил Р3 и R1. Но R1 = Р1 + Р2, откуда
R2 = Р1 + Р2 + Р3
Из конца силы R2 проведем четвертую, последнюю силу Р4. Соединив точку О с концом вектора силы Р4, получим силу R, равную сумме сил R2 и Р4, т. е.
R = R2 +Р4 = Р1 + Р2 + Р3 + Р4= ΣРi
Промежуточные векторы R1 и R2 можно не строить, а последовательно, в указанном выше порядке одну за другой отложить все заданные силы и начало первой соединить с концом последней.
Полученная таким образом фигура OABCD (см. рис.б) называется силовым многоугольником. Замыкающая сторона этого многоугольника представляет собой равнодействующую R заданной системы сил, равную их геометрической сумме.
Необходимо обратить внимание на то, что равнодействующая сила R всегда направлена от начала первого слагаемого к концу последнего слагаемого. Иными словами, стрелка равнодействующей силы всегда направлена навстречу обходу многоугольника, соответствующему последовательному сложению заданных сил (см. рис. б).
Сложение данных сил можно выполнить также, пользуясь правилом параллелограмма, но такой способ связан с более громоздкими построениями.
Если при построении силового многоугольника конец последней слагаемой силы совместится с началом первой, равнодействующая R системы сходящихся сил окажется равной нулю. В этом случае система сходящихся сил будет находиться в равновесии.
Замкнутость силового многоугольника данной системы сходящихся сил является геометрическим условием ее равновесия. Таким образом, для уравновешенной системы сходящихся сил вектор равнодействующей обращается в точку.
Иными словами, геометрическое (графическое) условие равновесия системы сходящихся сил — силовой многоугольник должен быть замкнут.
Источник
Геометрический способ сложения сходящихся сил
Геометрический способ сложения сходящихся сил
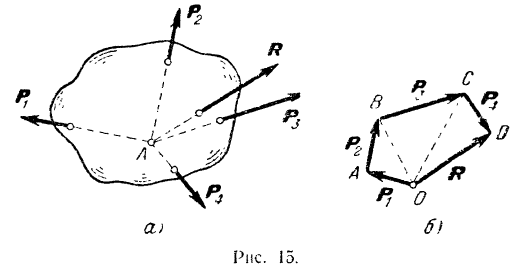
Системой сходящихся сил называется система сил, линии действия которых пересекаются в одной точке (рис. 15,а). Если мы перенесем все силы такой системы но линиям их действия в общую точку пересечения этих
линии, то, согласно первому следствию из аксиом статики, действие системы на абсолютно твердое тело не изменится. Таким образом, любую систему сходящихся сил можно заменить эквивалентной системой сил, приложенных в одной точке.
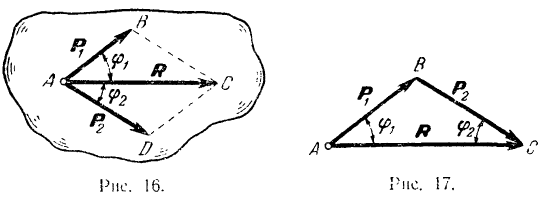
Задача о сложении двух сил, приложенных к одной точке, геометрически решается построением соответствующего параллелограмма сил (рис. 16) или силового треугольника (рис. 17), изображающего одну из половин параллелограмма.
Для построения силового треугольника из конца вектора одной силы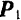 
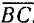
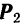
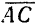
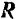
проводим вектор 
, изображающий вторую силу 
. Замыкающая сторона 
треугольника изображает но модулю и по направлению равнодействующую 
двух данных сходящихся сил.
Последовательно применяя правило треугольника, можно найти равнодействующую любого числа сходящихся сил, например четырех сил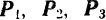 
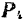
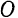
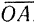
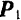
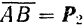
и 
(рис. 15, а). Для этого из_произвольной точки 
(рис. 15,6) отложим вектор 
, изображающий в принятом масштабе силу , из конца его— вектор 
, из его конца — вектор 
и т. д., помещая всякий раз начало следующего вектора в конце предыдущего, пока не исчерпаем все силы.
Полученный многоугольник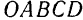 
, стороны которого в выбранном масштабе равны модулям составляющих сил и одинаково с ними направлены, называется силовым многоугольником.
Очевидно, что равнодействующая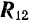 
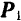
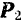
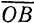
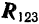
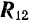
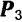
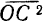
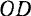
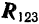
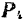
сил 
и 
изображается (рис. 15,6) вектором 
, равнодействующая 
сил и 
изображается вектором 
) и замыкающая сторона 
силового многоугольника, направленная от начала вектора первой силы к концу вектора последней, изображает в выбранном масштабе равнодействующую данной системы сходящихся сил (т. е. сил и ) как по модулю, так и по направлению.
Правило сложения сходящихся сил по способу многоугольника является общим правилом сложения любых векторов и называется их геометрическим сложением.
Геометрическая сумма всех сил любой системы называется главным вектором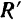 
этой системы
Таким образом, можно сказать, что равнодействующая 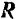системы сходящихся сил проходит через общую точку пересечения линий действия этих сил и равна по модулю и направлению их главному вектору.
Геометрическая сумма векторов не зависит от перемены мест слагаемых и, следовательно, при изменении порядка сложения сил их главный векгор не изменяется.
В частном случае трех сходящихся сил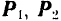 
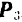
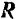
и 
не лежащих в одной плоскости (рис. 18), их равнодействующая изображается по модулю и направлению диагональю параллелепипеда, построенного на векторах составляющих сил (правило параллелепипеда).
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Возможно вам будут полезны эти дополнительные темы:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник
