- Методы графического сложения, вычитания
- Методы графического умножения, деления
- Сложение графиков функций
- 1. Введение
- 2. Основная часть «Сложение графиков функций»
- ПроСопромат.ру
- Технический портал, посвященный Сопромату и истории его создания
- Геометрический (графический) метод сложения сил, приложенных в одной точке
- Сумма векторов: графический метод, примеры, решенные упражнения.
- Содержание:
- Графический метод сложения векторов
- пример
- Частный случай: сумма параллельных векторов
- Примеры сложения векторов
- — Смещения
- Шаги к векторному сложению
- — Результирующая скорость
- Упражнение решено
- Решение
Методы графического сложения, вычитания
Чтобы построить график функции , надо построить на одном чертеже графики и , потом при каждом x сложить ординаты двух графиков.
Если необходимо построить график разности двух функций , то этот случай сводится к построению суммы: . Причем, график функции получается из графика функции симметричным отражением относительно оси .
В случае, когда вторая функция — константа, то графическое сложение означает сдвиг графика первой функции по вертикали на эту константу, причем, если константа положительная, то сдвиг осуществляется вверх, а если отрицательная, то вниз.
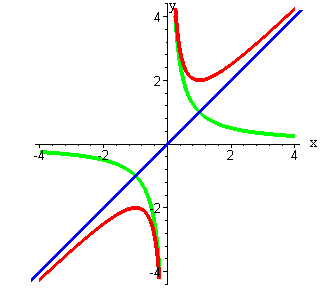 | 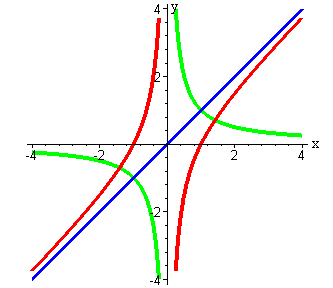 |
Сложение двух функций: 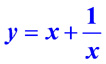 | Вычитание двух функций: 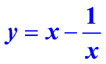 |
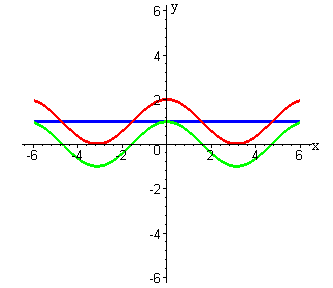 | 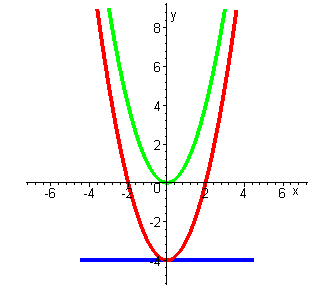 |
Сложение функции и константы:  | Вычитание функции и константы: 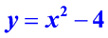 |
Методы графического умножения, деления
Чтобы построить график функции y=f(x)·g(x) , надо построить на одном чертеже графики y=f(x) и y=g(x) , потом при каждом x перемножить ординаты двух графиков.
Графическое деление выполняется аналогично произведению.
В частном случае при построении графика функции y=A·f(x) , где A — константа надо график функции y=f(x) растянуть в |A| раз по вертикали, при условии |A|≥1 , или сжать в 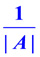
В данном параграфе рассмотрены следующие примеры:
Источник
Сложение графиков функций
2. Основная часть «Сложение графиков функций». 4
3. Заключение. 13
1. Введение
На уроках алгебры мы научились строить графики элементарных функций: линейных, квадратичных, обратно пропорциональной зависимости, логарифмической, показательной, степенной, тригонометрических функций. В 9м и 10м классах мы научились строить многие графики способом геометрических преобразований графиков функций параллельного переноса, сдвиг вдоль оси координат, сжатие и растяжение вдоль координатных осей. Среди таких преобразований я выделила построение графиков способом сложения. Действительно, многие функции можно представить в виде суммы нескольких функций:

функцию 

1. Изучить информацию по рассматриваемому вопросу в литературе, в том числе и в учебнике.
2. Выполнить практическое построение графиков функций, которые представляют собой сумму двух элементарных функций.
Теоретический материал по данному вопросу «Сложение графиков функций» я изучила по книгам: «Геометрические преобразования графиков функций» и «Графики функций» Справочник , , и другие. Из этих книг я узнала правила построения графиков методом сложения.
2. Основная часть «Сложение графиков функций»
На основании изученного материала, я пришла к выводу, что общий метод построения графиков суммы двух функций заключается в том, что предварительно строят два графика для обеих функций, а затем складывают ординаты этих кривых при одних и тех же значениях х (удобно — в характерных точках). По полученным точкам строят искомый график и выполняют проверку в нескольких контрольных точках.
В отдельных случаях построение графиков суммы функций можно выполнять так.
Если надо построить график суммы двух функций, то строят вначале график одной, более простой, функции, затем к нему пристраивают график второй функции, ординаты которого откладывают от соответствующих точек первого графика.
Построим график функции 
Строим графики функций-слагаемых 
Источник
ПроСопромат.ру
Технический портал, посвященный Сопромату и истории его создания
Геометрический (графический) метод сложения сил, приложенных в одной точке
Силы называют сходящимися, если их линии действия пересекаются в одной точке.
Различают плоскую систему сходящихся сил, когда линии действия всех данных сил лежат в одной плоскости, и пространственную систему сходящихся сил, когда линии действия сил лежат в разных плоскостях.
На основании следствия из третьей аксиомы, силу можно переносить по линии ее действия. Поэтому сходящиеся силы всегда можно перенести в одну точку, а именно, в точку пересечения их линий действия.
Рассмотрим плоскую систему сходящихся сил. На рис. а приведена такая система сил, линии действия которых пересекаются в точке К.
Пользуясь указанным следствием из третьей аксиомы, перенесем все силы в точку К. Такой перенос необходим для графического определения равнодействующей заданной системы сил.
Выполнив этот перенос, получим четыре силы Р1 , Р2 , Р3 и Р4 , приложенные в точке К. Для определения их равнодействующей сложим последовательно все данные силы, используя правило треугольника (рис.б).
Сложим сначала две силы Р1 и Р2. Из произвольной точки О проведем, сохраняя масштаб и направление, силу Р1. Из конца силы Р1 проведем вторую силу Р2. Соединив точку О с концом силы Р2, получим силу R1, равную сумме сил Р1 и Р2,
Из конца силы R1 проведем третью силу Р3. Соединив точку О с концом силы Р3, получим силу R2, равную сумме сил Р3 и R1. Но R1 = Р1 + Р2, откуда
R2 = Р1 + Р2 + Р3
Из конца силы R2 проведем четвертую, последнюю силу Р4. Соединив точку О с концом вектора силы Р4, получим силу R, равную сумме сил R2 и Р4, т. е.
R = R2 +Р4 = Р1 + Р2 + Р3 + Р4= ΣРi
Промежуточные векторы R1 и R2 можно не строить, а последовательно, в указанном выше порядке одну за другой отложить все заданные силы и начало первой соединить с концом последней.
Полученная таким образом фигура OABCD (см. рис.б) называется силовым многоугольником. Замыкающая сторона этого многоугольника представляет собой равнодействующую R заданной системы сил, равную их геометрической сумме.
Необходимо обратить внимание на то, что равнодействующая сила R всегда направлена от начала первого слагаемого к концу последнего слагаемого. Иными словами, стрелка равнодействующей силы всегда направлена навстречу обходу многоугольника, соответствующему последовательному сложению заданных сил (см. рис. б).
Сложение данных сил можно выполнить также, пользуясь правилом параллелограмма, но такой способ связан с более громоздкими построениями.
Если при построении силового многоугольника конец последней слагаемой силы совместится с началом первой, равнодействующая R системы сходящихся сил окажется равной нулю. В этом случае система сходящихся сил будет находиться в равновесии.
Замкнутость силового многоугольника данной системы сходящихся сил является геометрическим условием ее равновесия. Таким образом, для уравновешенной системы сходящихся сил вектор равнодействующей обращается в точку.
Иными словами, геометрическое (графическое) условие равновесия системы сходящихся сил — силовой многоугольник должен быть замкнут.
Источник
Сумма векторов: графический метод, примеры, решенные упражнения.
Содержание:
В векторная сумма это операция сложения между векторами, которая приводит к другому вектору. Векторы характеризуются величиной, а также направлением и смыслом. Следовательно, в общем случае невозможно сложить их, как это было бы со скалярными величинами, то есть путем сложения чисел.
Вектор, полученный из суммы нескольких векторов, называется результирующий вектор. В механике говорят о Равнодействующая сила, которая представляет собой векторную сумму всех сил, действующих на тело. Эта равнодействующая эквивалентна множеству или системе сил.
Чтобы полностью указать вектор суммы, необходимо указать величину и единицу, направление и смысл.
Важно отметить, что при сложении векторов они должны представлять одну и ту же физическую величину, поэтому векторная сумма является однородной операцией. Это означает, что мы можем добавлять одну силу к другой, но не силу со смещением, поскольку результат не имеет смысла.
Для нахождения результирующего вектора доступны несколько методов: графический и аналитический. Чтобы найти векторные суммы с помощью графических методов, мы начнем с простого представления вектора, а именно с ориентированного сегмента или стрелки, подобного этому:
Векторы обозначаются жирными буквами в печатном тексте или стрелкой над буквой, чтобы отличать их от соответствующих величин или скалярных величин. Например, величина вектора vЭто просто v.
Графический метод сложения векторов
Чтобы добавить более двух копланарных векторов, полигональный метод или метод траверса, который состоит из трансляции себя параллельно каждому из векторов слагаемых. Характерной чертой векторов является то, что они инвариантны относительно сдвига, поэтому мы будем использовать это свойство для определения суммы.
Мы начинаем с любого из векторов, так как сложение векторов коммутативно и порядок слагаемых не влияет на сумму. Затем переводится второй вектор, сопоставляя его начало с концом первого.
Затем он переносится к следующему вектору и помещается следующим, следуя той же процедуре, которая заключается в совпадении начала координат с концом предыдущего. Продолжайте таким образом, пока не будет установлен последний вектор.
Результирующий вектор — это тот, который соединяет начало первого со свободным концом последнего. Название этого метода происходит от получившегося рисунка: многоугольник.
пример
Возьмем для примера сумму двух векторов или Y v показано на рисунке выше.
Начиная с вектора или, переехал в вектор v чтобы его начало совпадало с концом первого. Результирующий вектор ш взят из происхождения или до конца v, образуя трехстороннюю фигуру: треугольник. Поэтому в этом частном случае процедура называется метод треугольника.
Обратите внимание на важную деталь: величина или модуль результирующего вектора не является суммой модулей добавленных векторов. Фактически, это почти всегда меньше, если векторы не параллельны.
Посмотрим, что происходит в этом случае ниже.
Частный случай: сумма параллельных векторов
Описанный метод применим и к частному случаю, когда векторы параллельны. Рассмотрим следующий пример:
Оставлено вектору v в исходном положении и переводится в вектор или таким образом, что его происхождение совпадает с концом v. Теперь нарисован вектор, начиная с начала координат v и заканчивает конец или.
Это результирующий вектор ш а его размер — это сумма размеров слагаемых. Направление и смысл трех векторов одинаковы.
Результирующий вектор имеет максимальный модуль, если слагаемые образуют угол 0º друг с другом, как в примере. Если векторы расположены под углом 180º друг к другу, то результирующий вектор имеет минимальный модуль.
Примеры сложения векторов
— Смещения
Велосипедист проезжает сначала 3 км в северном направлении, а затем 4 км на запад. Ваше перемещение, которое мы называем р, легко найти с помощью метода треугольника плюс система отсчета, где отмечены стороны света:
Шаги к векторному сложению
— Начальная точка совпадает с началом системы отсчета.
-По осям координат выбран масштаб, который в данном случае составляет 1 см = 1 км.
-Первое смещение нарисовано в масштабе d1.
-Следующий d1 второе смещение нарисовано d2, также в масштабе.
-В результате смещения р — вектор, идущий от начала до конца d2.
-Размерр измеряется градуированной линейкой, легко проверить, что R = 5.
-Наконец, угол, который р форма по горизонтали измерена с помощью транспортира и составляет θ = 37 0
— Результирующая скорость
Пловец хочет пересечь реку и для этого плывет со скоростью 6 км / ч перпендикулярно берегу, но его отклоняет течение со скоростью 4 км / ч.
Чтобы узнать его итоговую скорость, добавляются векторы скорости пловца, изображенного вертикально, и вектора скорости, отображаемого горизонтально.
Графическим методом получается результирующая скорость. vр:
Отклонение, которое испытывает пловец, можно рассчитать следующим образом:
θ = arctg (4/6) = 33,7º вправо от начального направления
Величина его скорости увеличивается благодаря тому, что скорость реки складывается векторно. Его можно найти, аккуратно установив масштаб, как в примере выше.
Или с помощью тригонометрических соотношений 33,7º:
грех 33,7º = 4 / vр
vр = 4 / sin 33,7º = 7,21 км / ч
Упражнение решено
На частицу действуют следующие силы, величины которых указаны ниже:
Найдите равнодействующую силу.
Решение
Мы можем складывать графически, начиная с любого из векторов, поскольку векторная сумма коммутативна.
На рисунке A мы начали с F1. Устанавливая масштаб, с помощью линейки и квадрата переносятся другие векторы, чтобы расположить их один за другим.
Вектор Fр направлено от происхождения F1 до конца F4. Его величина составляет 5,2 Н, и он образует угол 26,5 ° по отношению к горизонту.
На рисунке B была решена та же проблема, начиная с F3 и заканчивая F4, чтобы сравнятьсяFр .
Многоугольники разные, но результат тот же. Читатель может провести тест, снова изменив порядок векторов.
Источник







