Графический способ решения задачи это как

Решение задач линейного программирования графическим методом

Описание метода

Если в задаче линейного программирования имеется только две переменные, то ее можно решить графическим методом.

Рассмотрим задачу линейного программирования с двумя переменными и :
(1.1) ;
(1.2)
Здесь , есть произвольные числа. Задача может быть как на нахождение максимума (max), так и на нахождение минимума (min). В системе ограничений могут присутствовать как знаки , так и знаки .

Построение области допустимых решений

Графический метод решения задачи (1) следующий.
Вначале мы проводим оси координат и и выбираем масштаб. Каждое из неравенств системы ограничений (1.2) определяет полуплоскость, ограниченную соответствующей прямой.

Так, первое неравенство
(1.2.1)
определяет полуплоскость, ограниченную прямой . С одной стороны от этой прямой , а с другой стороны . На самой прямой . Чтобы узнать, с какой стороны выполняется неравенство (1.2.1), мы выбираем произвольную точку, не лежащую на прямой. Далее подставляем координаты этой точки в (1.2.1). Если неравенство выполняется, то полуплоскость содержит выбранную точку. Если неравенство не выполняется, то полуплоскость расположена с другой стороны (не содержит выбранную точку). Заштриховываем полуплоскость, для которой выполняется неравенство (1.2.1).

Тоже самое выполняем для остальных неравенств системы (1.2). Так мы получим заштрихованных полуплоскостей. Точки области допустимых решений удовлетворяют всем неравенствам (1.2). Поэтому, графически, область допустимых решений (ОДР) является пересечением всех построенных полуплоскостей. Заштриховываем ОДР. Она представляет собой выпуклый многоугольник, грани которого принадлежат построенным прямым. Также ОДР может быть неограниченной выпуклой фигурой, отрезком, лучом или прямой.

Может возникнуть и такой случай, что полуплоскости не содержат общих точек. Тогда областью допустимых решений является пустое множество. Такая задача решений не имеет.

Можно упростить метод. Можно не заштриховывать каждую полуплоскость, а вначале построить все прямые
(2)
Далее выбрать произвольную точку, не принадлежащую ни одной из этих прямых. Подставить координаты этой точки в систему неравенств (1.2). Если все неравенства выполняются, то область допустимых решений ограничена построенными прямыми и включает в себя выбранную точку. Заштриховываем область допустимых решений по границам прямых так, чтобы оно включало в себя выбранную точку.

Если хотя бы одно неравенство не выполняется, то выбираем другую точку. И так далее, пока не будет найдены одна точка, координаты которой удовлетворяют системе (1.2).

Нахождение экстремума целевой функции

Итак, мы имеем заштрихованную область допустимых решений (ОДР). Она ограничена ломаной, состоящей из отрезков и лучей, принадлежащих построенным прямым (2). ОДР всегда является выпуклым множеством. Оно может быть как ограниченным множеством, так и не ограниченным вдоль некоторых направлений.

Теперь мы можем искать экстремум целевой функции
(1.1) .

Для этого выбираем любое число и строим прямую
(3) .
Для удобства дальнейшего изложения считаем, что эта прямая проходит через ОДР. На этой прямой целевая функция постоянна и равна . такая прямая называется линией уровня функции . Эта прямая разбивает плоскость на две полуплоскости. На одной полуплоскости
.
На другой полуплоскости
.
То есть с одной стороны от прямой (3) целевая функция возрастает. И чем дальше мы отодвинем точку от прямой (3), тем больше будет значение . С другой стороны от прямой (3) целевая функция убывает. И чем дальше мы отодвинем точку от прямой (3) в другую сторону, тем меньше будет значение . Если мы проведем прямую, параллельную прямой (3), то новая прямая также будет линией уровня целевой функции, но с другим значением .

Таким образом, чтобы найти максимальное значение целевой функции, надо провести прямую, параллельную прямой (3), максимально удаленную от нее в сторону возрастания значений , и проходящую хотя бы через одну точку ОДР. Чтобы найти минимальное значение целевой функции, надо провести прямую, параллельную прямой (3) и максимально удаленную от нее в сторону убывания значений , и проходящую хотя бы через одну точку ОДР.

Если ОДР неограниченна, то может возникнуть случай, когда такую прямую провести нельзя. То есть как бы мы ни удаляли прямую от линии уровня (3) в сторону возрастания (убывания) , то прямая всегда будет проходить через ОДР. В этом случае может быть сколь угодно большим (малым). Поэтому максимального (минимального) значения нет. Задача решений не имеет.

Рассмотрим случай, когда крайняя прямая, параллельная произвольной прямой вида (3), проходит через одну вершину многоугольника ОДР. Из графика определяем координаты этой вершины. Тогда максимальное (минимальное) значение целевой функции определяется по формуле:
.
Решением задачи является
.

Также может встретиться случай, когда прямая параллельна одной из граней ОДР. Тогда прямая проходит через две вершины многоугольника ОДР. Определяем координаты и этих вершин. Для определения максимального (минимального) значения целевой функции, можно использовать координаты любой из этих вершин:
.
Задача имеет бесконечно много решений. Решением является любая точка, расположенная на отрезке между точками и , включая сами точки и .

Пример решения задачи линейного программирования графическим методом

Фирма выпускает платья двух моделей А и В. При этом используется ткань трех видов. На изготовление одного платья модели А требуется 2 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. На изготовление одного платья модели В требуется 3 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. Запасы ткани первого вида составляют 21 м, второго вида — 10 м, третьего вида — 16 м. Выпуск одного изделия типа А приносит доход 400 ден. ед., одного изделия типа В — 300 ден. ед.

Составить план производства, обеспечивающий фирме наибольший доход. Задачу решить графическим методом.

Пусть переменные и означают количество произведенных платьев моделей А и В, соответственно. Тогда количество израсходованной ткани первого вида составит:
(м)
Количество израсходованной ткани второго вида составит:
(м)
Количество израсходованной ткани третьего вида составит:
(м)
Поскольку произведенное количество платьев не может быть отрицательным, то
и .
Доход от произведенных платьев составит:
(ден. ед.)

Тогда экономико-математическая модель задачи имеет вид:

Решаем графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 7) и (10,5; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 10) и (10; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (8; 0).

Прямые и являются осями координат.

Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

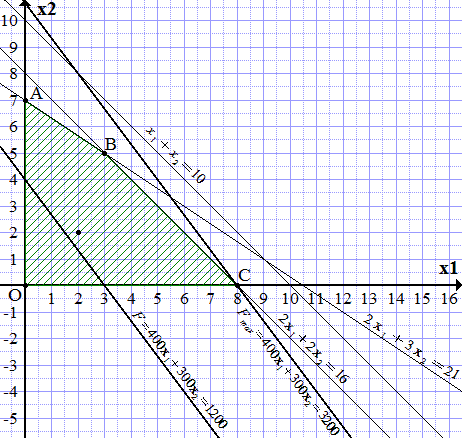
Заштриховываем область, чтобы точка (2; 2) попала в заштрихованную часть. Получаем четырехугольник OABC.

Строим произвольную линию уровня целевой функции, например,
(П1.1) .
При .
При .
Проводим прямую через точки (0; 4) и (3; 0).

Далее замечаем, что поскольку коэффициенты при и целевой функции положительны (400 и 300), то она возрастает при увеличении и . Проводим прямую, параллельную прямой (П1.1), максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку четырехугольника OABC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.

.
То есть, для получения наибольшего дохода, необходимо изготовить 8 платьев модели А. Доход при этом составит 3200 ден. ед.

Пример 2

Решить задачу линейного программирования графическим методом.

Решаем графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 6) и (6; 0).

Строим прямую .
Отсюда .
При .
При .
Проводим прямую через точки (3; 0) и (7; 2).

Строим прямую .
Строим прямую (ось абсцисс).

Область допустимых решений (ОДР) ограничена построенными прямыми. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

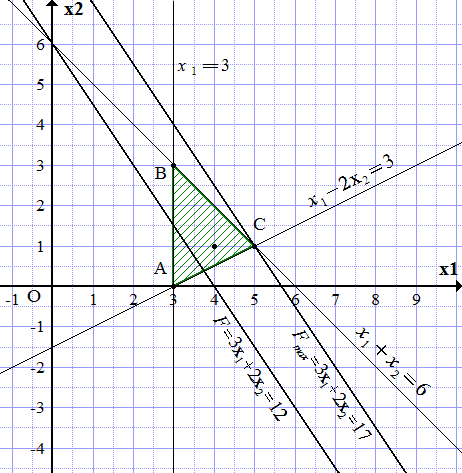
Заштриховываем область по границам построенных прямых, чтобы точка (4; 1) попала в заштрихованную часть. Получаем треугольник ABC.

Строим произвольную линию уровня целевой функции, например,
.
При .
При .
Проводим прямую линию уровня через точки (0; 6) и (4; 0).
Поскольку целевая функция увеличивается при увеличении и , то проводим прямую, параллельную линии уровня и максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку треугольника АВC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.

Пример отсутствия решения

Решить графически задачу линейного программирования. Найти максимальное и минимальное значение целевой функции.

Решаем задачу графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (2,667; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 3) и (6; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (3; 0) и (6; 3).

Прямые и являются осями координат.

Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

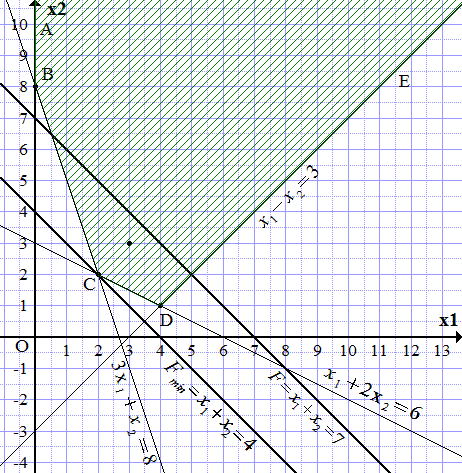
Заштриховываем область, чтобы точка (3; 3) попала в заштрихованную часть. Получаем неограниченную область, ограниченную ломаной ABCDE.

Строим произвольную линию уровня целевой функции, например,
(П3.1) .
При .
При .
Проводим прямую через точки (0; 7) и (7; 0).
Поскольку коэффициенты при и положительны, то возрастает при увеличении и .

Чтобы найти максимум, нужно провести параллельную прямую, максимально удаленную в сторону возрастания , и проходящую хотя бы через одну точку области ABCDE. Однако, поскольку область неограниченна со стороны больших значений и , то такую прямую провести нельзя. Какую бы прямую мы не провели, всегда найдутся точки области, более удаленные в сторону увеличения и . Поэтому максимума не существует. можно сделать сколь угодно большой.

Ищем минимум. Проводим прямую, параллельную прямой (П3.1) и максимально удаленную от нее в сторону убывания , и проходящую хотя бы через одну точку области ABCDE. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Минимальное значение целевой функции:

Максимального значения не существует.
Минимальное значение
.

Автор: Олег Одинцов . Опубликовано: 08-08-2016

Источник

Статья «Графический метод решения задач» по математике для обучающихся 7-11 классов

Графический метод решения задач.

В школьной практике в последнее время один из ведущих способов решения задач связан с алгебраическим (аналитическим) методом их решения, что указывает на определённый разрыв между методами решения задач, применяемыми в науке, технике, повседневной жизни.

Устранение, где это возможно, указанного разрыва является одной из важнейших проблем усиления политехнической направленности школьного курса обучения. В большей степени эта проблема вызвана тем, что существующие учебные и методические пособия не уделяют должного внимания различным методам решения задач. Между тем реализация их даёт большие возможности для совершенствования обучения математике. Для обеспечения дальнейшего повышения

качества обучения недостаточно совершенствовать лишь вычислительные методы математики, но необходимо также развивать и совершенствовать геометрические и графические методы, составляющие основы конструктивного мышления.

Графические методы и проецирование, как мне кажется, могут

успешно конкурировать и сочетаться с аналитическими , как отличающиеся большей наглядностью и простотой.

В своей практике я часто применяю этот метод для решения задач из разных тем и разделов алгебры и геометрии. В одной небольшой статье не представляется возможным сколь-нибудь обстоятельно раскрыть все аспекты. Для выявления определённых преимуществ графических методов перед аналитическими рассмотрю решения некоторых задач.

1 . Решение текстовых задач с использованием координатного метода.

Как уже отмечалось выше, один из ведущих способов решения текстовых задач связан с использованием уравнений, первое знаком-ство с которыми начинается в начальной школе. Обучающиеся пя-тых- шестых классов, по существу, решают текстовые задачи только составлением уравнения по их условию. Считаю чрезмерное

увлечение этим способом не вполне оправданным.

Некоторые задачи решаются проще арифметическим способом с использованием координатного луча. Замечу, что в процессе решения задач единичный отрезок явно не указывается, но подразумевается в каждой наглядной иллюстрации.

Задача 1. Турист часть пути прошёл пешком, часть проехал на вело-

сипеде, остальной путь проехал на машине. Пешком турист

преодолел путь, в четыре раза меньший, чем на велосипеде,

а на машине на 300 км. больший, чем пешком. Какой путь

турист прошёл пешком, если на машине он проехал на

60 км. больше, чем на велосипеде?

1 способ 2 способ

Пусть х км.- путь туриста пешком. Изобразим схематически

Тогда 4х км.- путь, проделанный движение туриста на раз-

на велосипеде, ( х + 300 )км., или ных участках его пути.

( 4х + 60 )км.- путь на машине. п:

Составим уравнение и решим его: в:

х + 300 = 4х + 60; м:

4х – х = 300 – 60; -60

3х = 240;

х = 80. Покажем, какова разница в

километрах между ними.

Из чертежа явно видно, что

Турист прошёл пешком 80 км.. в трёх частях пути 240 км.,

значит в одной части 80 км.

Рассмотрим ещё один пример:

Задача 2: Из деревни вышел пешеход, а через два часа вслед за ним

выехал велосипедист. Скорость велосипедиста 10 км/ч., а

скорость пешехода 5км/ч.. Через сколько времени после

своего выезда велосипедист догонит пешехода.

Решим задачу графически.

 ______  ______  ______  ______  _______________

Ответ: встреча произойдёт через два часа.

Ознакомление обучающихся с этим способом не потребует много времени, однако его применение поможет учителю в обучении решению задач.

Хочу отметить, что возможно и разумное сочетание рассмотренных способов, например, сначала изобразить наглядно условие задачи для лучшего его понимания, а после этого ввести х и составить уравнение по условию.

Использование координатного луча кроме непосредственной помощи в нахождении верного пути решения задачи формирует координатные представления обучающихся. Это, несомненно, станет дополнительной основой при дальнейшем изучении координатного метода.

2 . Графики равномерного движения при решении текстовых задач.

Задача 2. Из двух населённых пунктов А и В одновременно навстречу

друг другу выходят два туриста. При встрече оказывается,

что турист, вышедший из А, прошёл на 2 км. больше, чем

турист, вышедший из В. Продолжая движение с той же

скоростью, первый турист прибывает в В через 1 час 36мин.,

а второй в А – через 2 часа 30 мин.. Найдите расстояние АВ

и скорость каждого туриста.

Обычно при решении текстовых задач на движение для наглядности

пройденное расстояние изображают отрезком. Применение коорди-натной прямой для решения этой задачи вряд ли приведёт к его упро-щению. Этот недостаток можно устранить, применяя графическое представление движения, известное из курса физики.

Отмечу, что при решении задач на равномерное движение, если равны скорости, пройденные расстояния и промежутки времени, полезны соотношения:

Кроме того, напомню, что тангенс угла наклона прямой х = x ₀ + vt к оси О t численно равен скорости тела.

Источник