Графический способ решения задач пример

Содержание

Решение задач линейного программирования графическим методом
Описание метода
Построение области допустимых решений
Нахождение экстремума целевой функции
Пример решения задачи линейного программирования графическим методом
Пример 2
Пример отсутствия решения
Исследовательская работа Графический метод решения текстовых задач
Глава 2. Основные приемы решения задач с помощью графического метода.

Решение задач линейного программирования графическим методом

Описание метода

Если в задаче линейного программирования имеется только две переменные, то ее можно решить графическим методом.

Рассмотрим задачу линейного программирования с двумя переменными и :
(1.1) ;
(1.2)
Здесь , есть произвольные числа. Задача может быть как на нахождение максимума (max), так и на нахождение минимума (min). В системе ограничений могут присутствовать как знаки , так и знаки .

Построение области допустимых решений

Графический метод решения задачи (1) следующий.
Вначале мы проводим оси координат и и выбираем масштаб. Каждое из неравенств системы ограничений (1.2) определяет полуплоскость, ограниченную соответствующей прямой.

Так, первое неравенство
(1.2.1)
определяет полуплоскость, ограниченную прямой . С одной стороны от этой прямой , а с другой стороны . На самой прямой . Чтобы узнать, с какой стороны выполняется неравенство (1.2.1), мы выбираем произвольную точку, не лежащую на прямой. Далее подставляем координаты этой точки в (1.2.1). Если неравенство выполняется, то полуплоскость содержит выбранную точку. Если неравенство не выполняется, то полуплоскость расположена с другой стороны (не содержит выбранную точку). Заштриховываем полуплоскость, для которой выполняется неравенство (1.2.1).

Тоже самое выполняем для остальных неравенств системы (1.2). Так мы получим заштрихованных полуплоскостей. Точки области допустимых решений удовлетворяют всем неравенствам (1.2). Поэтому, графически, область допустимых решений (ОДР) является пересечением всех построенных полуплоскостей. Заштриховываем ОДР. Она представляет собой выпуклый многоугольник, грани которого принадлежат построенным прямым. Также ОДР может быть неограниченной выпуклой фигурой, отрезком, лучом или прямой.

Может возникнуть и такой случай, что полуплоскости не содержат общих точек. Тогда областью допустимых решений является пустое множество. Такая задача решений не имеет.

Можно упростить метод. Можно не заштриховывать каждую полуплоскость, а вначале построить все прямые
(2)
Далее выбрать произвольную точку, не принадлежащую ни одной из этих прямых. Подставить координаты этой точки в систему неравенств (1.2). Если все неравенства выполняются, то область допустимых решений ограничена построенными прямыми и включает в себя выбранную точку. Заштриховываем область допустимых решений по границам прямых так, чтобы оно включало в себя выбранную точку.

Если хотя бы одно неравенство не выполняется, то выбираем другую точку. И так далее, пока не будет найдены одна точка, координаты которой удовлетворяют системе (1.2).

Нахождение экстремума целевой функции

Итак, мы имеем заштрихованную область допустимых решений (ОДР). Она ограничена ломаной, состоящей из отрезков и лучей, принадлежащих построенным прямым (2). ОДР всегда является выпуклым множеством. Оно может быть как ограниченным множеством, так и не ограниченным вдоль некоторых направлений.

Теперь мы можем искать экстремум целевой функции
(1.1) .

Для этого выбираем любое число и строим прямую
(3) .
Для удобства дальнейшего изложения считаем, что эта прямая проходит через ОДР. На этой прямой целевая функция постоянна и равна . такая прямая называется линией уровня функции . Эта прямая разбивает плоскость на две полуплоскости. На одной полуплоскости
.
На другой полуплоскости
.
То есть с одной стороны от прямой (3) целевая функция возрастает. И чем дальше мы отодвинем точку от прямой (3), тем больше будет значение . С другой стороны от прямой (3) целевая функция убывает. И чем дальше мы отодвинем точку от прямой (3) в другую сторону, тем меньше будет значение . Если мы проведем прямую, параллельную прямой (3), то новая прямая также будет линией уровня целевой функции, но с другим значением .

Таким образом, чтобы найти максимальное значение целевой функции, надо провести прямую, параллельную прямой (3), максимально удаленную от нее в сторону возрастания значений , и проходящую хотя бы через одну точку ОДР. Чтобы найти минимальное значение целевой функции, надо провести прямую, параллельную прямой (3) и максимально удаленную от нее в сторону убывания значений , и проходящую хотя бы через одну точку ОДР.

Если ОДР неограниченна, то может возникнуть случай, когда такую прямую провести нельзя. То есть как бы мы ни удаляли прямую от линии уровня (3) в сторону возрастания (убывания) , то прямая всегда будет проходить через ОДР. В этом случае может быть сколь угодно большим (малым). Поэтому максимального (минимального) значения нет. Задача решений не имеет.

Рассмотрим случай, когда крайняя прямая, параллельная произвольной прямой вида (3), проходит через одну вершину многоугольника ОДР. Из графика определяем координаты этой вершины. Тогда максимальное (минимальное) значение целевой функции определяется по формуле:
.
Решением задачи является
.

Также может встретиться случай, когда прямая параллельна одной из граней ОДР. Тогда прямая проходит через две вершины многоугольника ОДР. Определяем координаты и этих вершин. Для определения максимального (минимального) значения целевой функции, можно использовать координаты любой из этих вершин:
.
Задача имеет бесконечно много решений. Решением является любая точка, расположенная на отрезке между точками и , включая сами точки и .

Пример решения задачи линейного программирования графическим методом

Фирма выпускает платья двух моделей А и В. При этом используется ткань трех видов. На изготовление одного платья модели А требуется 2 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. На изготовление одного платья модели В требуется 3 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. Запасы ткани первого вида составляют 21 м, второго вида — 10 м, третьего вида — 16 м. Выпуск одного изделия типа А приносит доход 400 ден. ед., одного изделия типа В — 300 ден. ед.

Составить план производства, обеспечивающий фирме наибольший доход. Задачу решить графическим методом.

Пусть переменные и означают количество произведенных платьев моделей А и В, соответственно. Тогда количество израсходованной ткани первого вида составит:
(м)
Количество израсходованной ткани второго вида составит:
(м)
Количество израсходованной ткани третьего вида составит:
(м)
Поскольку произведенное количество платьев не может быть отрицательным, то
и .
Доход от произведенных платьев составит:
(ден. ед.)

Тогда экономико-математическая модель задачи имеет вид:

Решаем графическим методом.
Проводим оси координат и .

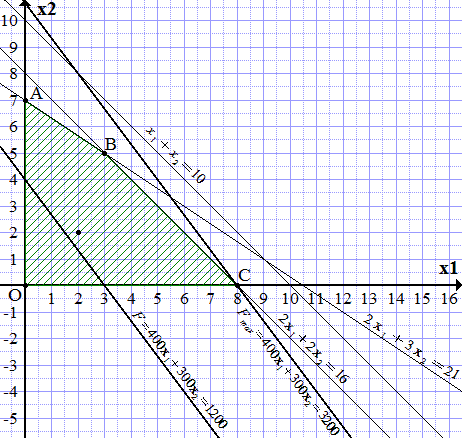
Строим прямую .
При .
При .
Проводим прямую через точки (0; 7) и (10,5; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 10) и (10; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (8; 0).

Прямые и являются осями координат.

Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

Заштриховываем область, чтобы точка (2; 2) попала в заштрихованную часть. Получаем четырехугольник OABC.

Строим произвольную линию уровня целевой функции, например,
(П1.1) .
При .
При .
Проводим прямую через точки (0; 4) и (3; 0).

Далее замечаем, что поскольку коэффициенты при и целевой функции положительны (400 и 300), то она возрастает при увеличении и . Проводим прямую, параллельную прямой (П1.1), максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку четырехугольника OABC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.

.
То есть, для получения наибольшего дохода, необходимо изготовить 8 платьев модели А. Доход при этом составит 3200 ден. ед.

Пример 2

Решить задачу линейного программирования графическим методом.

Решаем графическим методом.
Проводим оси координат и .

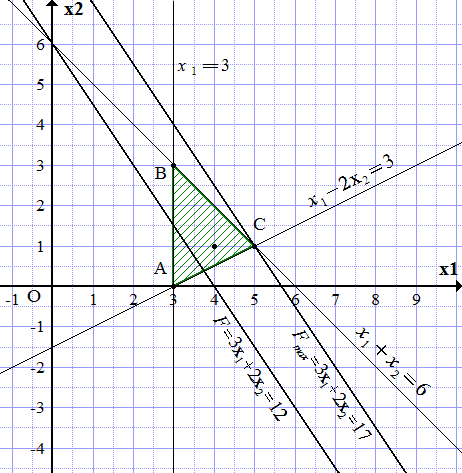
Строим прямую .
При .
При .
Проводим прямую через точки (0; 6) и (6; 0).

Строим прямую .
Отсюда .
При .
При .
Проводим прямую через точки (3; 0) и (7; 2).

Строим прямую .
Строим прямую (ось абсцисс).

Область допустимых решений (ОДР) ограничена построенными прямыми. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

Заштриховываем область по границам построенных прямых, чтобы точка (4; 1) попала в заштрихованную часть. Получаем треугольник ABC.

Строим произвольную линию уровня целевой функции, например,
.
При .
При .
Проводим прямую линию уровня через точки (0; 6) и (4; 0).
Поскольку целевая функция увеличивается при увеличении и , то проводим прямую, параллельную линии уровня и максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку треугольника АВC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.

Пример отсутствия решения

Решить графически задачу линейного программирования. Найти максимальное и минимальное значение целевой функции.

Решаем задачу графическим методом.
Проводим оси координат и .

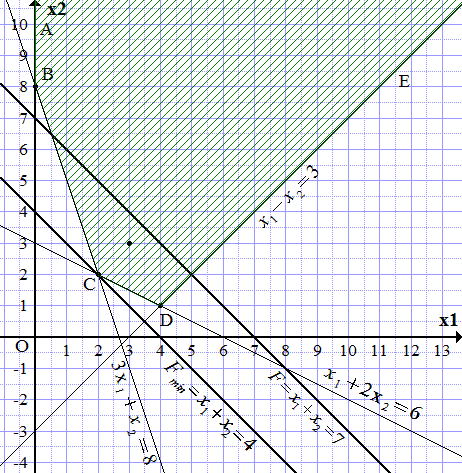
Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (2,667; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 3) и (6; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (3; 0) и (6; 3).

Прямые и являются осями координат.

Заштриховываем область, чтобы точка (3; 3) попала в заштрихованную часть. Получаем неограниченную область, ограниченную ломаной ABCDE.

Строим произвольную линию уровня целевой функции, например,
(П3.1) .
При .
При .
Проводим прямую через точки (0; 7) и (7; 0).
Поскольку коэффициенты при и положительны, то возрастает при увеличении и .

Чтобы найти максимум, нужно провести параллельную прямую, максимально удаленную в сторону возрастания , и проходящую хотя бы через одну точку области ABCDE. Однако, поскольку область неограниченна со стороны больших значений и , то такую прямую провести нельзя. Какую бы прямую мы не провели, всегда найдутся точки области, более удаленные в сторону увеличения и . Поэтому максимума не существует. можно сделать сколь угодно большой.

Ищем минимум. Проводим прямую, параллельную прямой (П3.1) и максимально удаленную от нее в сторону убывания , и проходящую хотя бы через одну точку области ABCDE. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Минимальное значение целевой функции:

Максимального значения не существует.
Минимальное значение
.

Автор: Олег Одинцов . Опубликовано: 08-08-2016

Источник

Исследовательская работа Графический метод решения текстовых задач

«Графический метод решения текстовых задач»

Киреева Людмила Александровна

учитель математики первой категории МБОУ

«Лицей №6 г. Горно-Алтайска»

Известно, что некоторые задачи алгебры очень трудно решить аналитическим путем. Поэтому любое представление условия задачи в виде рисунка или чертежа облегчает их решение.

В данной работе представлен графический метод решения задач, который основан на наглядно-геометрических интерпретациях, связанных с построением графического образа задачи на координатной плоскости. Таким образом, выбранная тема актуальна и перспективна. Из-за сложности, нестандартности графический метод решения задач в школьном курсе математики не изучается.

Проблема: Появились совершенно новые типы задач, не входящие в действующие школьные учебники, при решении которых необходимо практическое применение свойств, которые раньше заучивались лишь теоретически.

Гипотеза: решение задач графическим методом является наглядным представлением условий в виде рисунка или чертежа, что помогает глубже понять условие задачи, делает его более наглядным, значительно упрощает решение.

Предмет исследования: графический метод решения задач

Цель: изучить графический метод решения задач, а также области его применения.

Изучить историю применения графического метода для решения задач различных видов.

Рассмотреть различные типы задач, методом решения которых может являться график.

Выявить плюсы и минусы этого метода, в сравнении с другими способами решения задач.

Выяснить области применения графического метода решения задач.

Глава 1. История применения графического метода для решения задач

Древние греки в 6–4 вв. до н.э. решали уравнения с неизвестными посредством геометрических построений. Были разработаны специальные построения для выполнения сложения, вычитания, умножения и деления отрезков, извлечения квадратных корней из длин отрезков; ныне этот метод называется геометрической алгеброй.

Они решали задачи на построение и смотрели, при каких значениях задача имеет решение, изучали, сколько решений может иметь эта задача, и т.д. Величайшим математическим физиком древности был Архимед. Для доказательства теорем механики он использовал геометрические соображения.

Приведение задач к геометрическому виду имело ряд важных последствий. В частности, числа стали рассматриваться отдельно от геометрии, поскольку работать с несоизмеримыми отношениями можно было только с помощью геометрических методов. Геометрия стала основой почти всей строгой математики по крайней мере до 17 века. И даже в 18 веке, когда уже были достаточно развиты алгебра и математический анализ, строгая математика трактовалась как геометрия, и слово «геометр» было равнозначно слову «математик».

Глава 2. Основные приемы решения задач с помощью графического метода.

Очень многие текстовые задачи на составление уравнений (или систем уравнений) можно решать графически. Графическое изображение функций, описывающих условие задачи – зачастую удобный технический прием.

Задачи на движение

Задачи на совместную работу

Задачи на смеси и сплавы

Задачи с параметрами

Решение, как известно, осуществляется двумя приемами: либо точными построениями при помощи инструментов (конструктивный прием), либо обоснованными вычислениями (вычислительный прием):

Конструктивный приём (чисто графический). График вычерчивается как можно более точно непосредственно по значениям величин, входящих в условие задачи. Построения делаются циркулем, линейкой на миллиметровой бумаге. Ответ получается обычно приближенный, но приемлемый для практических целей; мы находим его при помощи измерений длин отрезков или других элементов чертежа, или просто «читаем» ответ на чертеже.

Вычислительный прием (графико – вычислительный). График применяется как условное изображение связи между рассматриваемыми величинами. Решение задачи осуществляется на точных геометрических соотношениях.

Решение текстовой задачи графическим способом осуществляется в три этапа:

Построение графической модели задачи.

Решение получившейся графической задачи.

Перевод полученного ответа с графического языка на естественный.

Глава 3. Задачи на движение

Немаловажное значение в математике имеют задачи на движение. Задачи на движение подразделяются на следующие типы: по количеству движущихся объектов, по направлению движущихся объектов, по времени начала движения.

Задача 1 см. в Приложении 1

Из пункта O в пункт N вышел пешеход. Одновременно с ним из пункта N в пункт O выехал велосипедист, который встретил пешехода через 50 минут после своего выезда из N. Сколько времени понадобится пешеходу для того, чтобы пройти весь путь, если известно, что велосипедист проделал бы весть путь на 4 часа быстрее пешехода.

Построим график зависимости пройденного пешеходом и велосипедистом пути от времени (Рис.1). Пусть p(x) – зависимость пройденного пешеходом пути от времени x, w(x) — зависимость пройденного велосипедистом пути от времени x (Полное решение см. в Приложении 2).

Глава 4. Задачи на работу

В задачах на работу речь идёт, как правило, о какой-то деятельности.

Задачу 3 и ее решение смотрите в Приложении 3.

Двое рабочих, выполняя задание вместе, могли бы закончить его за 12 дней. Если сначала будет работать только один из них, а когда он выполнит половину всей работы, его сменит второй рабочий, то всё задание будет закончено за 25 дней. За сколько дней каждый рабочий в отдельности может выполнить всё задание?

Предположим, что первый рабочий работает быстрее, чем второй. Отрезок AN – график работы первого рабочего, а отрезок BD – график работы второго рабочего (Рис. 2 смотрите в Приложении 4).

AQ изображает время совместной работы; AQ=12 ч. Проведем NKǁBD, тогда AK=50, QK=38

x ₁ =18 не подходит, т.к. первый рабочий работает быстрее. Тогда время первого 12 + 8 = 20 дней, а второго 38 8=30 дн.

Ответ: первый за 20 дней, а второй за 30 дней.

Глава 5. Задачи на смеси и сплавы

Задачи на смеси и сплавы считаются сложными.

Задачу 5 и ее решение смотрите в Приложении 5.

В 100г 20%-ного раствора соли добавили 300г её 10%-ного раствора. Определите процентную концентрацию раствора.

Отрезок прямой (основание графика) представляет собой общую массу смеси, а на осях ординат откладывают точки, соответствующие массовым долям растворенного вещества в исходных растворах. Соединив прямой точки на осях ординат, получают прямую, которая отображает функциональную зависимость массовой доли растворенного вещества в смеси от массы смешанных растворов в обратной пропорциональной зависимости. (Рис. 3)

Глава 6. Задачи с параметром

Изучение многих физических процессов, химических, экономических и многих других закономерностей имеют практическую направленность и часто приводят к решению задач с параметрами, которые бывают весьма сложными и требующими нестандартного подхода к решению. Аналитические (алгебраические) методы решения задач с параметрами довольно громоздки, требуют аккуратности выкладок, умения не «потерять решение», проверить всевозможные значения параметра.

В современной жизни решение уравнений с параметрами является неотъемлемой частью выпускных и вступительных экзаменов в различные учебные заведения, поэтому очень важно понять и разобраться с этой темой ещё в школе.

Сколько корней в зависимости от а имеет уравнение ?

Перепишем уравнение в виде . Решим его в системе координат ( Оху ). Для этого построим графики функций и . (Рис. 4)

Ответ: Если , то уравнение имеет два корня; если , то уравнение имеет один корень; если , то корней нет.

Задача 8 и ее решение в Приложении 6.

Одно из преимуществ графического метода перед алгебраическим, состоит в наглядности решения, что позволяет лучше понять задачу. Использование этого метода упрощает решение задач: нет громоздких вычислений. График дает возможность определить, есть ли у данной задачи решение и единственно ли оно. Есть и «минусы»: иногда получаются приближённые значения в случаях неудачного масштаба или очень трудно вообще отыскать решение.

Современная наука и техника очень широко использует графики. График – международный язык техники.

Кроме того, в ходе освоения графического метода решения текстовых задач формируются практические навыки. Графический метод решения таких задач позволяет провести параллель с физикой, где использование системы координат достаточно часто применяется при решении физических задач. Также графический метод позволяет решать некоторые задачи из химии, например, рассмотренные нами задачи на смеси и сплавы.

Целью данной работы было изучение применения графиков линейной функции в решении текстовых задач. В процессе работы над данной темой, выяснилось, что при решении текстовых задач наряду с традиционными методами, можно использовать и графический метод. Были изучены материалы учебно-методической литературы. Решены задачи из экзаменационных материалов разными способами.

Гипотеза подтвердилась частично. Графический метод упрощает решение задач. Но есть и минусы, о которых было сказано выше. Настоящее исследование значительно расширило представление о линейной функции, способствовало глубокому пониманию взаимосвязи этой функции с реальными ситуациями, возникающими в нашей жизни. Есть планы продолжить исследование в этом направлении и более детально рассмотреть графико-геометрический метод, который основан на подобии треугольников.

Быков А.А. Сборник задач по математике. – М.:Изд..дом ГУ ВШЭ,2008

Генкель Г.З. «Геометрические решения негеометрических задач», — Москва: Просвещение 2007.

Кочагин В.В. ОГЭ 2018. Математика: тематические тренировочные задания: 9 класс. – Москва: Эксмо, 2017. – 192 с.

Лысенко Ф.Ф. Учимся решать задачи с параметром. Ростов-на-Дону:

Лунина Л.С. Обучение решению алгебраических задач геометрическим методом //Математика в школе: М.: Изд. «Школа-Пресс»,1996.-№4.- с.34-39.

Окунев А.А. Графическое решение уравнений с параметрами. – М.: ШколаПресс,1996.

Пирютко О. Н. «Графический метод решения текстовых задач» — Минск.: Новое знание,2010

Рудин В.Н., Рудина Е.И. Графическое решение текстовых задач. Учебное пособие по математике для учителей и учащихся. Издание Томского института повышения квалификации работников образования, 1995 г.

Савин А. П. Занимательные математические задачи. – М.: АСТ, 1995.

Сергеев И. Н. Математика. Задачи с ответами и решениями. Учебное пособие. – М.: Бином, 2004.

Шарыгин И. Ф. Факультативный курс по математике. Решение задач. Учебное пособие для 10 класса средней школы. – М.: Просвещение, 1989.

Из пункта A вышла грузовая машина со скоростью 60 км/ч. Через 2 ч вслед за ней из А вышла легковая машина со скоростью 90 км/ч. На каком расстоянии от пункта А легковая машина догонит грузовую?

За начальный отсчет времени берется момент выхода грузовой машины, тогда момент выхода легковой машины будет через два часа. Зная скорости движения объектов, построим графики движения (Рис. 5). По чертежу видно, что точка пересечения графиков показывает встречу машин, она состоялась на расстоянии 360 км.