Графический способ решения систем неравенств с двумя переменными 9 класс

Графическое решение систем неравенств с двумя переменными

В презентации на конкретных примерах представлен способ решения систем неравенств с двумя переменными на координатной плоскости. Материал предназначен для объяснения темы «Системы неравенств с двумя переменными».в 9 классе (Алгебра, 9 класс, автор Макарычев Ю.Н.)

Просмотр содержимого документа
«Графическое решение систем неравенств с двумя переменными»

с двумя переменными

К учебнику Ю.Н.Макарычева

Алгебра, 9 класс, Глава III §

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

Решение системы неравенств

с двумя переменными

Решением системы неравенств с двумя переменными называется пара значений этих переменных, являющаяся как решением первого неравенства, так и второго неравенства системы.

Изображение множества решений неравенства с двумя переменными на координатной плоскости

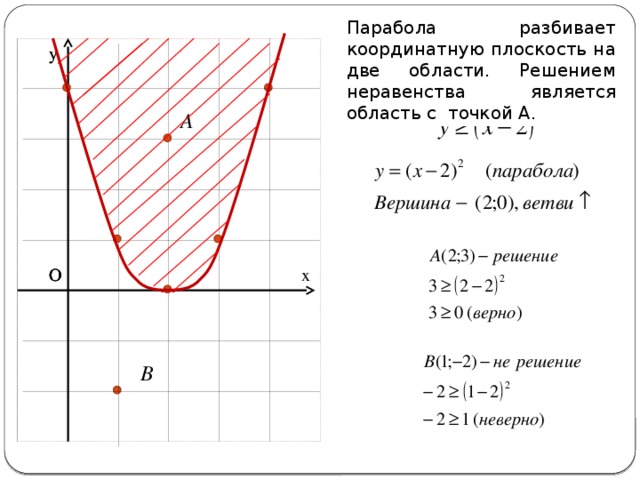
Парабола разбивает координатную плоскость на две области. Решением неравенства является область с точкой А.

Изображение множества решений системы неравенств с двумя переменными на координатной плоскости

Множеством решений системы неравенств с двумя переменными является пересечение множеств решений неравенств, входящих в систему. На координатной плоскости множество решений системы неравенств изображается множеством точек, являющихся общей частью множеств, представляющих собой решения каждого неравенства системы.

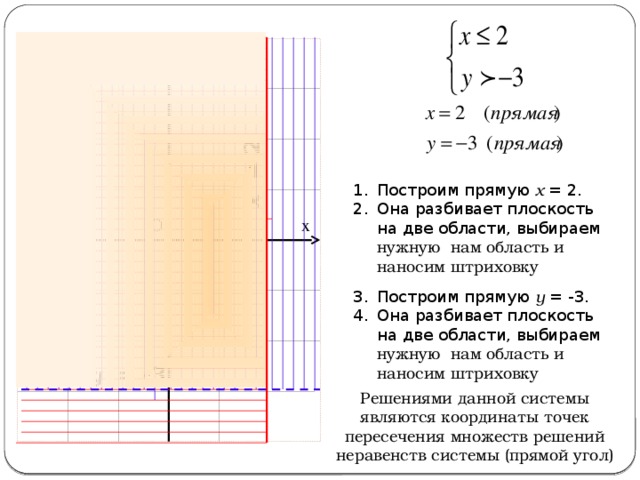
• Построим прямую х = 2.
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим прямую у = -3.
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (прямой угол)

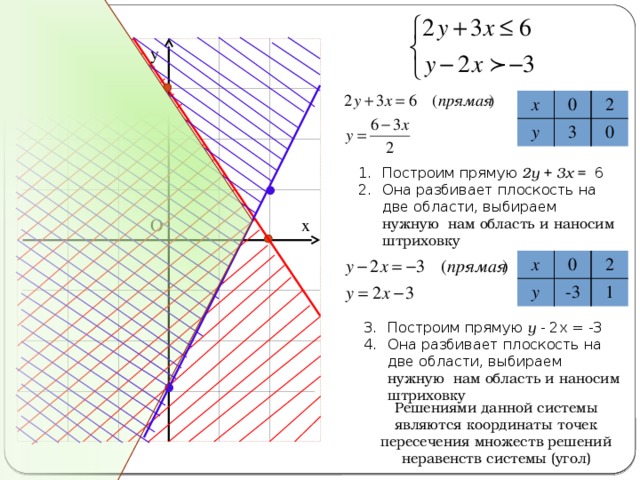
• Построим прямую 2у + 3х = 6
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим прямую у — 2х = -3
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (угол)

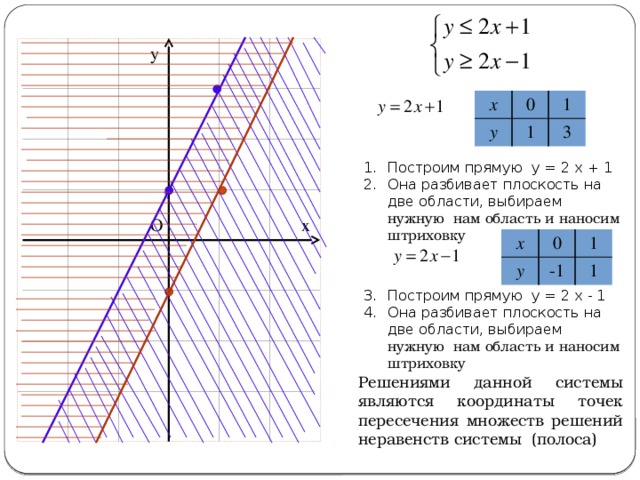
• Построим прямую у = 2 х + 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим прямую у = 2 х — 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (полоса)

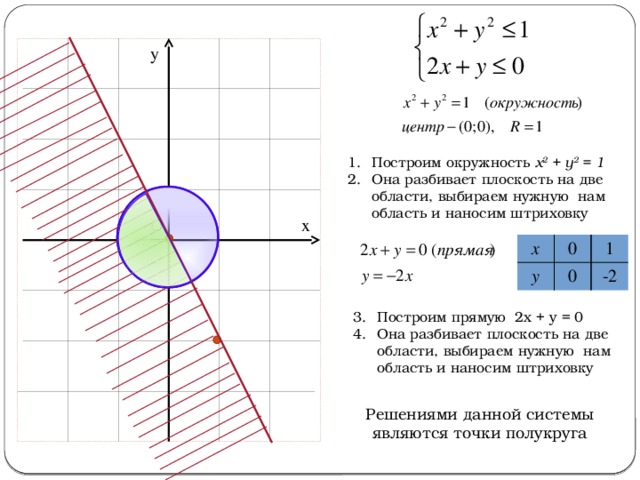
• Построим окружность х2+ у2= 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим прямую 2х + у = 0
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются точки полукруга

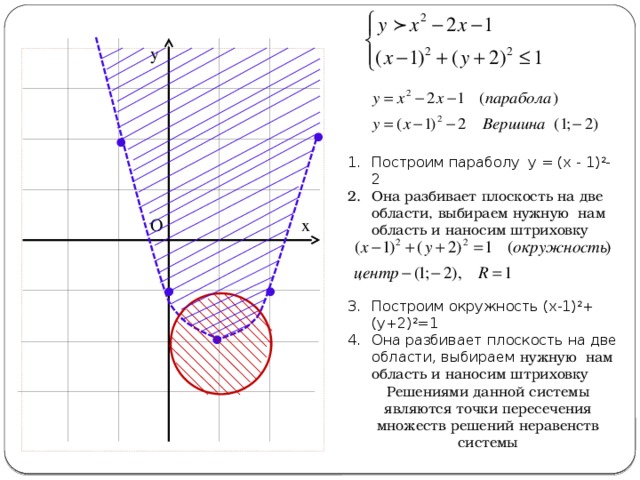
• Построим параболу у = (х — 1) 2 -2
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим окружность (х-1) 2 +(у+2) 2 =1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются точки пересечения множеств решений неравенств системы

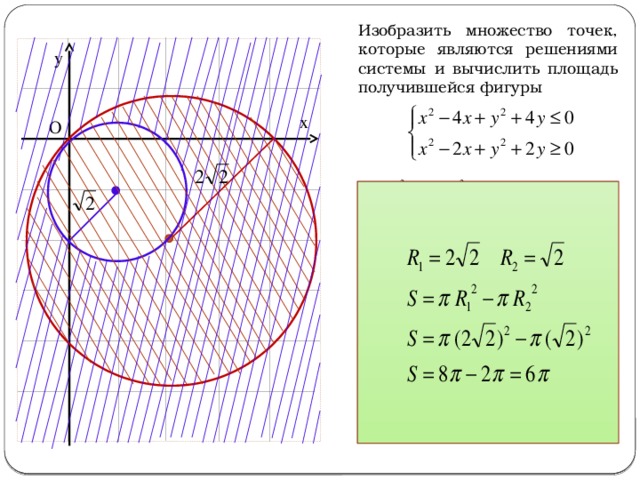
Изобразить множество точек, которые являются решениями системы и вычислить площадь получившейся фигуры

Источник

Системы неравенств с двумя переменными

п.1. Алгоритм графического решения системы неравенств с двумя переменными

Найти на координатной плоскости множество решений системы неравенств: $$ \left\< \begin < l >\mathrm & \\ \mathrm & \end\right. $$ Множество решений – сегмент круга, отсекаемый отрезком AB. Сам отрезок в множество решений не входит.

п.2. Примеры

Пример 1. Найдите на координатной плоскости множество решений системы неравенств.

Выразим y(x) в явном виде

Строим прямые, заштриховываем области над ними, находим пересечение.

Выразим y(x) в явном виде

Заштриховываем область под первой параболой и над второй параболой.

Выразим y(x) в явном виде

Строим гиперболу и прямую. Заштриховываем области под гиперболой и над прямой.

Заштриховываем области вне первой окружности и внутри второй.

Находим пересечение – кольцо.

Пример 2. Задайте системой неравенств треугольник с вершинами
A(2; 3), B(4; 4), C(3; 0)
Уравнения прямых, на которых лежат стороны треугольника:

Источник

Графическое решение неравенств с двумя переменными
презентация к уроку по алгебре (9 класс) на тему

Урок-объяснение нового материала- «Графическое решение неравенств, систем неравенств с двумя переменными.», в 9 классе, с углубленным изучением математики.

Скачать:

Вложение	Размер
neravenstva.rar	217.38 КБ

Предварительный просмотр:

Урок алгебры в 9 классе

Графическое решение неравенств, систем неравенств с двумя переменными.

Учитель математики Прокофьева И.Л.

МБОУ лицей №8 г. Ставрополь

Цели и задачи урока:

1. Ввести понятие системы неравенств с двумя переменными.

Составить алгоритм решения систем неравенств

Формировать навыки решения систем неравенств

2. Развивать « критическое» мышление и интерес к предмету у учащихся в процессе решения проблемных ситуаций и заданий творческого характера.

Оборудование: Ноутбук , мультимедийный проектор,

• Организация начала занятия.
• Проверка выполнения домашнего задания.
• Подготовка к усвоению новых знаний.
• Изучение нового материала.
• Первичная проверка знаний.
• Закрепление знаний.
• Подведение итогов занятий.
• Домашнее задание.

Ход урока. 1. Организационный момент.

На предыдущих уроках мы решали системы уравнений графическим способом. Сегодня мы переходим к изучению новой темы «Графическое решение неравенств, систем неравенств с двумя переменными». Повторим материал прошлого урока.

1. Устная работа учащихся с использованием проектора.

Из данных 6 функций выберите те, которые будут изображаться на экране.

Даны функции (записаны на доске)

• 

3 .Изучение новой темы .

Неравенство с двумя неизвестными можно представить так: f(x;y) > , где f(x;y), – многочлен двух переменных х и у . Его можно записать в виде .

Неравенства содержащие неизвестные могут быть вида

F(x,y) 0, F(x,y) 0, F(x,y) 0.

• Решением неравенства называется упорядоченная пара действительных чисел , обращающая это неравенство в верное числовое неравенство.
• Графически это соответствует заданию точки координатной плоскости.
• Решить неравенство — значит найти множество его решений

Если одно из неравенств системы представлено в виде нестрогого неравенства, то график изображается сплошной линией, если строгое, то пунктирной.

Если одно из неравенств системы представлено в виде у ≥f(x). То это неравенство задает на плоскости область, которая лежит не ниже графика.

Если одно из неравенств системы представлено в виде у ≤f(x). То это неравенство задает на плоскости область, которая лежит не ниже графика.

Если линия f(x.у)- замкнутая, например окружность, или замкнутая ломанная , то неравенство f(x.у≥0, задает область лежащую внутри замкнутой линии., а неравенство f(x.у)≤0 — область лежащую вне.

И наиболее универсальное, полезное для проверки правило- Правило пробной точки

• Построить F(x;y)=0
• Взяв из какой — либо области пробную точку установить, являются ли ее координаты решением неравенства
• Сделать вывод о решении неравенства

Рассмотрим многочлен F(x;y)=y+x-1, тогда

В следующем примере дано уравнение окружности.

Необходимо расставить знаки неравенств >, ,используя правило пробной точки О(0,0).

1. Решить неравенство:│х-0,5│-1,5≤0
2. Решить неравенство:
3. Решить неравенство:

Системой неравенств с двумя переменными является система вида.

Алгоритм решения систем неравенств.

• Построить F(x;y)=0 и G(x;y)=0
• Взяв из каждой области пробную точку установить, являются ли ее координаты решением системы

Объединение полученных областей- решение системы неравенств

• Решаем вместе .

1. Решить систему неравенств:

2. Решить систему неравенств:

3 Решить графически неравенство:

Подведение итогов урока. Домашнее задание.

1. Ю.Н.МакарычевН.Г.Миндюк, К.Н.Нешков Алгебра. 9кл. учебник для класса с углубленным изучением математики Изд. Мнемозина, 2004-2006
2. Мордкович А.Г. . Алгебра, 9 кл. Учебник для классов с углубленным изучением математики. Изд. Мнемозина, 2004-2006
3. Мордкович А.Г. . Алгебра, 9 кл. Задачник для классов с углубленным изучением математики. Изд. Мнемозина, 2004-2006
4. А. Корянов Неравенства с двумя переменными: графическое и аналитическое решения Библиотека «Первого сентября, серия «Математика», выпуск 22,Москва, Чистые пруды,2008

По теме: методические разработки, презентации и конспекты

Презентация по теме «Решение неравенств с двумя переменными»

Данная презентация наглядно показывает графический способ решения неравенств с двумя переменными.

«Графическое решение уравнений с двумя переменными»

Урок по теме «Графическое решение уравнений с двумя переменными» разработан для учащихся 7 классов по программе учебника «Алгебра 7» Ю.Н. Макарычев, Н.Г. Миндюк и др. под ред. С.А. Теляковского.

Графическое решение неравенств c одной переменной. Графический способ решения систем уравнений.

Алгебра. Повторение. Подготовка к ГИА. 9 класс.

Решение неравенств и систем неравенств с двумя переменными

Алгебра.Повторение. Подготовка к ГИА. 9 класс.

Уравнения и неравенства с двумя переменными и их геометрическое решение

Разработка комплекса уроков содержит задания, аналитическое и графическое решения.Предназначена для подготовки к ЕГЭ.

Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем

Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.

Графическое решение неравенств с двумя переменными

Графическое решение неравенств с двумя переменными.

Источник

Алгебра

А Вы уже инвестируете?
Слышали про акцию в подарок?

Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб

План урока:

Уравнения с двумя переменными

Порою в ур-нии содержится не одна, а две переменных. Такие ур-ния мы уже изучали в 7 классе. Приведем несколько примеров уравнений с двумя переменными:

В абсолютном большинстве таких задач для обозначения переменных используют буквы х и у. Решение указывают в виде пары чисел, причем на первом месте пишут значение х, а на втором – значение у. Например, несложно убедиться, что пара чисел (– 1; 3) является решением ур-ния

Для этого надо лишь вместо х подставить (– 1), а вместо у – число 3:

Получили верное равенство. Заметим, что пара (– 1; 3) является не единственным решением ур-ния. Например, пара (2; 0) также обращает ур-ние в верное рав-во:

У ур-ний с двумя неизвестными, как и у ур-ний с одной неизвестной, можно определить степень. Для этого надо представить их в таком виде, когда слева записан многочлен, а справа – ноль. Тогда степень ур-ния будет равна степени многочлена. Так как ур-ние содержит две переменных, то для обозначения такого многочлена используется запись Р(х; у).

Пример. Определите степень уравнения

Решение. Раскроем скобки слева, а потом перенесем все слагаемые в одну сторону:

х 3 + ху – х – 1 = 0

В левой части стоит многочлен третьей степени (подробнее об определении степени полинома можно узнать из этого урока). Поэтому и степень ур-ния равна 3.

График уравнения с двумя переменными

Очень часто ур-ние с 2 переменными имеет бесконечное число решений. Их удобно изображать в виде графика, ведь каждой паре чисел (х₁; у₁) соответствует точка на координатной плоскости с координатами х₁ и у₁.

Проще всего строить график уравнения с двумя переменными в том случае, когда удается выразить переменную у через х. Например, пусть надо построить график ур-ния

Выразим неизвестную величину у через х, то есть попытаемся получить ф-цию у = у(х):

Построим график ф-ции у = 3 – 2х. Он одновременно будет являться и графиком ур-ния 6х + 3у = 9:

Не всегда можно так преобразовать ур-ние, чтобы получилась ф-ция у = у(х). Действительно, по определению функции, каждому значению аргумента должно соответствовать только одно значение ф-ции. Однако рассмотрим пример ур-ния

Можно убедиться, что его обращают в верное рав-во пары чисел (1; 1) и (1; – 1):

Получается, что одному значению х(х = 1) соответствует сразу 2 значения у (у = 1 и у = –1). Это значит, что графиком такого ур-ния не может являться ф-ция у = у(х)

В данном случае возможно выразить х через у. Перенесем слагаемое у 2 вправо:

Получили «перевернутую ф-цию» х = х(у), где не у зависит от х, а х от у. Ф-ция является квадратичной, а потому ее графиком будет парабола:

Так как х и у в ф-ции поменялись местами, то ось параболы стала не вертикальной, а горизонтальной.

Встречаются случаи, когда из ур-ния невозможно получить ни ф-цию у(х), ни ф-цию х(у). Рассмотрим ур-ние

Его решениями являются пары чисел (0; 5) и (0; – 5). То есть значению х = 0 соответствует два значения у (5 и – 5), поэтому не получиться записать ф-цию у(х). С другой стороны, решениями ур-ния являются также пары (5; 0) и (– 5; 0), то есть значению у = 0 также соответствует два значения х (– 5 и 5), поэтому и записать ф-цию х(у) не удастся. Вообще данное ур-ние является частным случаем ур-ния

где R– некоторое постоянное число, или параметр. Оно называется уравнением окружности, потому что его графиком как раз и является окружность.

Докажем это утверждение. Пусть на координатной плоскости есть точка А с произвольными координатами (х; у):

Опустим из А перпендикуляр на ось Ох в точку В. Получили прямоугольный треугольник ОАВ. Его катет ОВ равен у, а катет АВ = х. По теореме Пифагора можно найти длину гипотенузы ОА, которая и является расстоянием от О до А:

ОА 2 = ОВ 2 + АВ 2 = х 2 + у 2

Окружность радиусом R– это множество точек, удаленных от центра на расстояние R. То есть расстояние ОА равно R, то точка А лежит на окружности радиусом R c центром в О:

х 2 + у 2 = ОА 2 = R 2

Таким образом, координаты любой точки, лежащей на расстоянии Rот центра, удовлетворяют ур-нию

В частности, графиком ур-ния

является окружность с радиусом 5 (так как 25 = 5 2 )

Система уравнений с двумя переменными

Рассмотрим задачу. Разность двух чисел равна единице, а сумма их квадратов составляет 25. Чему равны эти два числа?

В задаче неизвестны два числа. Поэтому обозначим их за неизвестные величины х и у. Первое условие задачи, «разность чисел равна 1», можно записать ур-нием:

Второе условие записывается так:

Нам надо найти такие х и у, которые удовлетворяют одновременно обоим условиям задачи. То есть необходимо решить систему уравнений с двумя переменными:

Напомним, что в 7 классе мы уже изучали сис-мы ур-ний, однако рассматривались только случаи, когда все они являлись линейными. В рассматриваемом случае второе ур-ние линейным НЕ является (потому что переменные величины стоят во второй степени).

Для каждого ур-ния построим отдельный график. Точки их пересечения и будут соответствовать решениям сис-мы. Ур-ниех 2 + у 2 = 25 задает окружность. Ур-ние х – у = 1 будет совпадать с графиком линейной ф-ции у = х – 1:

Графики пересеклись в двух точках: (4; 3) и (– 3; – 4). Подставив их в сис-му, можно убедиться, что именно эти пары чисел являются решениями этой сис-мы.

Конечно, графический метод решения сис-м не всегда точный. Однако он позволяет оценить количество корней и их примерное расположение. Также графики помогают при изучении сис-м, содержащих параметры.

Пример. Найдите с помощью графиков решение сис-мы ур-ний

Решение. Построим графики каждого ур-ния. График первого ур-ния представляет собой параболу, а второй график – это прямая у = 4 – х:

Видно, что графики пересеклись в двух точках: (– 1; 5) и (4; 0). Убедиться в точности построения можно, просто подставив эти значения в решаемую сис-му.

Пример. При каком а сис-ма ур-ний

имеет ровно 3 решения?

Решение. Преобразуем 2-ое ур-ние сис-мы:

График ур-ния х 2 + у 2 = 9 представляет собой окружность радиусом 3. График у = – х 2 + а является параболой с ветвями, смотрящими вниз. Покажем на плоскости различные варианты взаимного расположения этих графиков при различных значениях параметра а:

Видно, что 3 точки пересечения у параболы и окружности может быть только в случае, если вершина параболы касается окружности в точке (0; 3). Для этого парабола должна определяться ур-нием у = – х 2 + 3. Это значит, что только при значении а = 3 сис-ма имеет 3 решения.

Метод подстановки

Конечно, решать сис-му ур-ний графическим способом не очень удобно, так как часто можно получить лишь приближенный ответ. При изучении систем линейных уравнений с двумя переменными мы познакомились с двумя универсальными способами их решения: методы подстановки и сложения. К сожалению, для нелинейных сис-м нет универсальных методов их решения. Однако тот же способ подстановки иногда может помочь.

Его суть заключается в том, что в одном ур-нии надо выразить одну переменную через другую. В результате получится ф-ция у(х) или х(у), и ее можно будет подставить во второе ур-ние и тем самым получить ур-ние с одной неизвестной. Иногда такое действие называют исключением переменной.

Пример. Найдите решение сис-мы уравнений методом подстановки:

Решение. Сразу видно, что во втором ур-нии можно выразить у через х:

Подставим выражение у = х 2 – 6 в первое ур-ние:

2х 2 + х – 3у – 16 = 0

2х 2 + х – 3(х 2 – 6) – 16 = 0

Получилось ур-ние, в котором уже нет у! Его достаточно легко решить, ведь оно сводится к квадратному ур-нию:

2х 2 + х – 3(х 2 – 6) – 16 = 0

2х 2 + х – 3х 2 + 18 – 16 = 0

D = b 2 – 4ас = 1 2 – 4•(– 1)•2 = 1 + 8 = 9

Получили два возможных значения х. Теперь выполним обратную подстановку:

Итак, имеем две пары чисел, (– 1; – 5) и (2; – 2), которые являются решениями сис-мы ур-ний.

Ответ: (– 1; 5); (2; – 2)

Пример. При каких х и у справедлива сис-ма

Решение. Попробуем найти решение методом подстановки. Из второго ур-ния следует, что ни одна из переменных не равна нулю, ведь иначе бы произведение ху равнялось бы не 7, а нулю. Поэтому можно поделить второе ур-ние на х:

У нас получилось выразить у через х. Подставим полученное выражение в первое ур-ние:

Заменим переменную х 2 на t:

Умножим ур-ние на t. Так как х ≠ 0, то и t≠ 0,поэтому мы можем смело производить подобное умножение:

t 2 – 50t + 49 = 0

Получили квадратное ур-ние. Можно честно решить его, однако мы поступим проще. По теореме Виета, произведение корней ур-ния должно равняться 49 (свободный член ур-ния), а в сумме они должны давать 50 (второй коэффициент ур-ния с противоположным знаком). Под эти условия подходят числа 1 и 49:

На всякий случай подставим их в квадратное ур-ние и убедимся, что они действительно являются его корнями:

1 2 – 50•1 + 49 = 1 – 50 + 49 = 0

49 2 – 50•49 + 49 = 2401 – 2450 + 49 = 0

Итак, имеем два корня: t₁ = 1 и t₂ = 49.

Теперь произведем обратную замену:

х 2 = 1 или х 2 = 49

Имеем два квадратных ур-ния. Корнями первого являются числа

У ур-ния х 2 = 49 корни – это числа

Получили четыре значения х. Для каждого из них можно вычислить соответствующее значение у по формуле у = 7/х:

при х = –1; у = 7/ – 1 = – 7

при х = 1; у = 7/1 = 7

при х = – 7; у = 7/– 7 = – 1

при х = 7; у = 7/7 = 1

В итоге имеем 4 пары решений: (– 1; – 7), (1; 7), (– 7; – 1) и (7; 1).

Ответ: (– 1; – 7), (1; 7), (– 7; – 1), (7; 1).

Метод сложения

Очевидно, что не всегда в ур-нии можно выразить одну переменную через другую. Такую ситуацию можно, например, наблюдать в сис-ме

Однако здесь в каждом ур-нии есть слагаемое 6у 2 , взятое с разными знаками. За счет этого сис-му можно решить методом сложения, ведь при сложении левых частей ур-ний слагаемые 6у 2 и (– 6у 2 ) сократятся, что позволит исключить переменную у из ур-ния. Для этого надо сложить по отдельности левые и правые части ур-ний и получить новое ур-ние:

(3х 2 – 6у 2 + 3х) + (– 2х 2 + 6у 2 ) = –18 + 22

3х 2 – 6у 2 + 3х – 2х 2 + 6у 2 = 4

Получили ур-ние, не содержащее у. Его можно решить как обычное квадратное ур-ние:

D = b 2 – 4ас = 3 2 – 4•1•(– 4) = 9 + 16 = 25

Нашли два значения х. Подставляя его второе ур-ние, получим

– 2•(– 4) 2 + 6у 2 = 22

Имеем 4 решения сис-мы (– 4; 3), (– 4; – 3), (1; – 2), (1; 2).

Мы рассмотрели простейший случай использования метода сложения уравнений, когда ур-ния сис-мы можно сложить сразу. Однако порою их надо сначала умножить на какие-то числа, и лишь потом складывать.

Пример. Укажите решение для сис-мы:

Решение. Сразу складывать эти ур-ния нет смысла, потому что при этом не исчезнет ни одна переменная. Напомним, что обе части любого ур-ния можно умножить на число, не равное нулю, и в результате получится равносильное ур-ние. Поэтому второе ур-ние умножим на (– 2):– 4х 2 + 2у 2 = – 2

А вот теперь есть смысл сложить его с первым ур-нием, так как у них есть слагаемые 2у 2 с противоположными знаками:

(3х 2 – 2у 2 ) + (– 4х 2 + 2у 2 ) = 1 – 2

Полученные значения х будем подставлять в другое ур-ние, например, в 2х 2 – у 2 = 1 (на самом деле можно выбрать любое другое из ур-ний сис-мы).

Теперь подставим х = 1:

В итоге получаем 4 решения: (– 1; – 1), (– 1; 1), (1; – 1) и (1; 1)

Ответ:(– 1; – 1), (– 1; 1), (1; – 1), (1; 1).

Порою метод сложения и метод подстановки следует использовать одновременно.

Пример. Решите систему методом сложения:

Решение: постараемся избавиться от слагаемых с буквенной частью ху. Для этого умножим второе ур-ние на (– 2):

– 2х – 2у – 2ху = 12

Сложим его с первым ур-нием:

(3х + у + 2ху) + (– 2х – 2у – 2ху) = – 6 + 12

исключить переменную не удалось, однако мы получили линейное ур-ние. Выразим из него у:

Теперь можно подставить это выражение, например, во второе ур-ние системы:

х + (х – 6) + х(х – 6) = – 6

х = 0 или х – 4 = 0

Подставим полученные результаты в выражение у = х – 6

Получили два решения: (0; – 6) и (4; – 2).

Ответ: (0; – 6) и (4; – 2).

Разложение левой части уравнения на множители

Если нельзя использовать ни метод подстановки, ни способ сложения, то могут помочь другие методы. Например, иногда в одном ур-нии справа можно оставить ноль, а слева – разложить многочлен на множители.

Пример. Решите систему:

Решение. В верхнем ур-нии можно выполнить следующие преобразования:

9х 2 – у 2 = 3х – у

(3х – у)(3х + у) = (3х – у)

(3х – у)(3х + у) – (3х – у) = 0

Можно заметить, что в левой части находится разность двух выражений, содержащих множитель (3х – у). Этот множитель можно вынести за скобки, при этом вместо второго выражения останется только единица, ведь его можно переписать как (3х – у)•1 (при умножении на единицу любое выр-ние остается неизменным):

(3х – у)(3х + у) – (3х – у)•1 = 0

(3х – у)(3х + у – 1) = 0

Вспомним, что произведение равно нулю, если один из его сомножителей нулевой. Поэтому

3х – у = 0 или 3х + у – 1 = 0

у = 3х или у = 1 – 3х

Получили два возможных варианта выражения для у. Будем подставлять их во второе ур-ние:

х = 0 или – 2х + 3 = 0

Найдем значение у, учитывая, что у = 3х:

Имеем решения (0; 0) и (1,5; 4,5). Далее рассмотрим второй случай, когда у = 1 – 3х:

х 2 + (1 – 3х) = х(1 – 3х)

х 2 + 1 – 3х = х – 3х 2

Перенося слагаемые влево, получаем квадратное ур-ние:

х 2 + 1 – 3х – х + 3х 2 = 0

D = b 2 – 4ас = (– 4) 2 – 4•4•1 = 0

Получаем, что у квадратного ур-ния есть лишь один корень:

Найдем соответствующее ему значение у:

Получили третье решение: (0,5; – 0,5).

Ответ: (0; 0); (1,5; 4,5);(0,5; – 0,5).

Системы ур-ний часто используются при решении геометрических задач.

Пример. Площадь прямоугольного треугольника равна 150 см 2 . Известно, что один из его катетов больше другого на 5 см. Каков периметр треугольника?

Решение. Традиционно катеты обозначают буквами а и b. Площадь прямоугольного треугольника равна половине произведения катетов:

Отсюда следует ур-ние:

Будем считать, что катет а больше, чем b. Тогда из условия можно записать

Итак, получается система:

Очевидно, что систему можно решить подстановкой а = 5 + b

b 2 + 5b – 300 = 0

Решая это квадратное ур-ние, легко получить два значения b: 20 и (– 15). По смыслу задачи длина катета должна измеряться положительным числом, а потому b = 20. Второй катет на 5 см меньше, то есть он равен 20 – 5 = 15 см. Длину гипотенузы с можно найти по теореме Пифагора:

с 2 = а 2 + b 2 = 20 2 + 15 2 = 625

Периметр треугольника – это сумма его сторон, она равна 25 + 20 + 15 = 60 см.

Линейное неравенство с двумя переменными

Изучение неравенств с двумя переменными начнем с простейших из них – линейных неравенств. Их можно получить из линейных ур-ний, поставив вместо знака «=» один из четырех знаков сравнения.

Приведем примеры линейных неравенств с двумя переменными:

– 18,4x + 45,325y + 54,36 0

Пример. Отметьте на координатной прямой все решения неравенства с двумя переменными

Решение. Рассмотрим ур-ние

Перенеся часть слагаемых вправо, можно получить функцию

Построим ее график. Он представляет собой параболу, которая разбивает плоскость на две области:

Для определения того, выполняется ли нер-во в той или иной области, достаточно рассмотреть по одной точке в каждой из областей. Начнем с внутренней области. К ней относится начало координат, точка (0; 0). Подставив х = 0 и у = 0 в нер-во, мы увидим, что оно выполняется:

Во второй области выполняется обратное нер-во у – х 2 + 5 2 + 5 4 + 2х 2 у + у 2 > 0

Решение. Изучим ур-ние

х 4 + 2х 2 у + у 2 = 0

В левой части стоит квадрат суммы слагаемых х 2 и у:

(х 2 + у) 2 = (х 2 ) 2 + 2х 2 у + у 2 = х 4 + 2х 2 у + у 2

С учетом этого ур-ние можно переписать так:

Построим график и определим, какое нер-во выполняется в полученных областях. В области I возьмем точку (0; – 1). При ее подстановке в исходное нер-во получаем:

0 4 + 2•0 2 (– 1) + (– 1) 2 > 0

Однако и в области II выполняется то же самое нер-во. Это можно увидеть на примере точки (0; 1):

0 4 + 2•0 2 •1 + 1 2 > 0

Получается, что решениями нер-ва являются точки обеих областей. То есть надо заштриховать всю координатную плоскость, кроме самой кривой у = – х 2 , которую мы покажем из-за этого штрихпунктирной линией:

Отдельно отметим, что возможны случаи, когда график ур-ния разбивает плоскость не на две, а на большее кол-во областей. В качестве примера можно привести нер-во

Ему соответствует ур-ние ху – 5 = 0

Из него можно получить функцию у = 5/х, графиком которой является гипербола. Этот график образует 3 области. Будем действовать как и раньше – выберем из каждой области по одной точке и посмотрим, выполняется ли на нем нер-во ух – 5 > 0. Из области I возьмем точку (– 5; – 5):

ху – 5 = (– 5)•(– 5) – 5 = 25 – 5 > 0

Из II области выберем точку (5; 5):

ху – 5 = 5•5 – 5 = 20 > 0

Наконец, из III области возьмем точку (0; 0):

ху – 5 = 0•0 – 5 = 0 – 5 2 + у 2 = 9 является окружность радиусом 3, то решением первого нер-ва является круг:

Нер-во х – у > 0 является линейным. Его решением будет полуплоскость:

Теперь совместим два полученных решения. Решением системы нер-в будет пересечение заштрихованных областей. Ведь именно здесь оба нер-ва системы будут выполняться одновременно. Это пересечение представляет собой полукруг (он заштрихован квадратиками):

Пример. Постройте решение системы нер-в

Решение. Построим графики ур-ний х 2 – у = 2 и у 2 – х = 2. Первый из них будет являться параболой у = х 2 – 2. Второй же будет выглядеть, как парабола, повернутая на 90°. Это будет функция х = у 2 – 2:

В том, что мы выбрали правильную область на плоскости, можно убедиться, просто подставив одну из ее точек, в частности (0; 0), в систему:

Источник