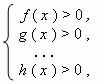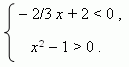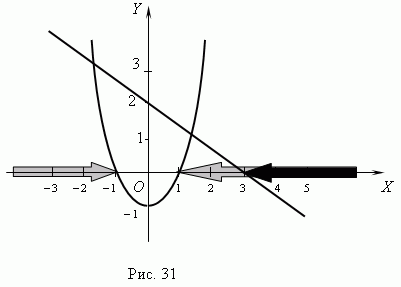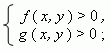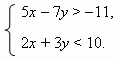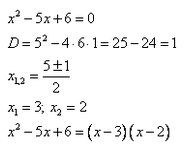Графическое решение неравенств
Приближённое решение неравенств.
Графическое решение неравенств с одним неизвестным.
Графическое решение систем неравенств с двумя неизвестными.
Графическое представление функций позволяет приближённо решать неравенства с одним неизвестным и системы неравенств с одним и двумя неизвестными. Чтобы решить графически неравенство с одним неизвестным, необходимо перенести все его члены в одну часть, т. e . привести к виду:
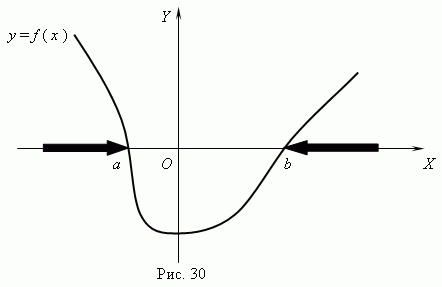
и построить график функции y = f ( x ). После этого, используя построенный график, можно найти нули функции (см. выше), которые разделят ось Х на несколько интервалов. Теперь на основе этого определим интервалы x , внутри которых знак функции соответствует знаку неравенства. Например, нули нашей функции: a и b ( рис.30 ). Тогда из графика очевидно, что интервалы, внутри которых f ( x ) > 0: x a и x > b ( они выделены жирными стрелками ). Ясно, что знак > здесь условный; вместо него может быть любой другой:
Чтобы решить графически систему неравенств с одним неизвестным, нужно перенести в каждом из них все члены в одну часть, т. e . привести неравенства к виду:
и построить графики функций y = f ( x ), y = g ( x ) , . , y = h ( x ). Каждое из этих неравенств решается графическим методом, описанным выше. После этого нужно найти пересечение решений всех неравенств, т. e . их общую часть.
П р и м е р . Решить графически систему неравенств:
Р е ш е н и е . Сначала построим графики функций y = — 2 / 3 x + 2 и
Решением первого неравенства является интервал x > 3, обозначенный на рис.31 чёрной стрелкой; решение второго неравенства состоит из двух интервалов: x — 1 и x > 1, обозначенных на рис.31 серыми стрелками.
Из графика видно, что пересечением этих двух решений является интервал x > 3. Это и есть решение заданной системы неравенств.
Чтобы решить графически систему двух неравенств сдвумя неизвестными, надо:
1) в каждом из них перенести все члены в одну часть, т. e . привести
нера венства к виду:
2) построить графики функций, заданных неявно: f ( x , y ) = 0 и g ( x , y ) = 0;
3) каждый их этих графиков делит координатную плоскость на две части:
в одной из них неравенство справедливо, в другой – нет; чтобы решить
графически каждое из этих неравенств, достаточно проверить
справедливость неравенства в одной произвольной точке внутри любой
части плоскости; если неравенство имеет место в этой точке, значит
эта часть координатной плоскости является его решением, если нет – то
решением является противоположная часть плоскости ;
4) решением заданной системы неравенств является пересечение
(общая область) частей координатной плоскости.
П р и м е р . Решить систему неравенств:
Р е ш е н и е . Сначала строим графики линейных функций: 5 x – 7 y = — 11 и
2 x + 3 y = 10 ( рис.32 ). Для каждой из них находим полуплоскость,
внутри которой соответствующее заданное неравенство
справедливо. Мы знаем, что достаточно проверить справедливость
неравенства в одной произвольной точке области; в данном
случае легче всего использовать для этого начало координат O ( 0, 0 ).
Подставляя его координаты в наши неравенства вместо x и y ,
получим: 5 · 0 – 7 · 0 = 0 > — 11, следовательно, нижняя
полуплоскость ( жёлтого цвета ) является решением первого
неравенства; 2 · 0 + 3 · 0 = 0 неравенство
имеет своим решением также нижнюю полуплоскость ( голубого
цвета ). Пересечение этих полуплоскостей ( область цвета бирюзы )
является решением нашей системы неравенств.
Источник
Метод интервалов, решение неравенств
О чем эта статья:
Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
 |
где x — переменная,
Квадратное неравенство можно решить двумя способами:
- графический метод;
- метод интервалов.
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два корня;
- D
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.
Если неравенство со знаком
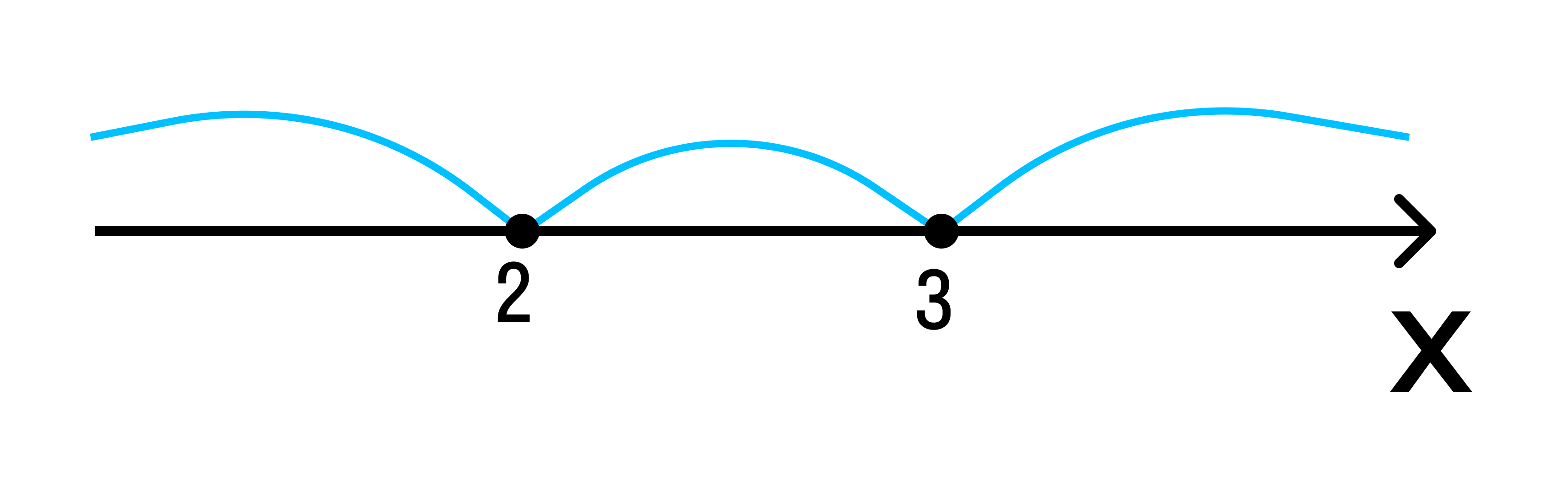
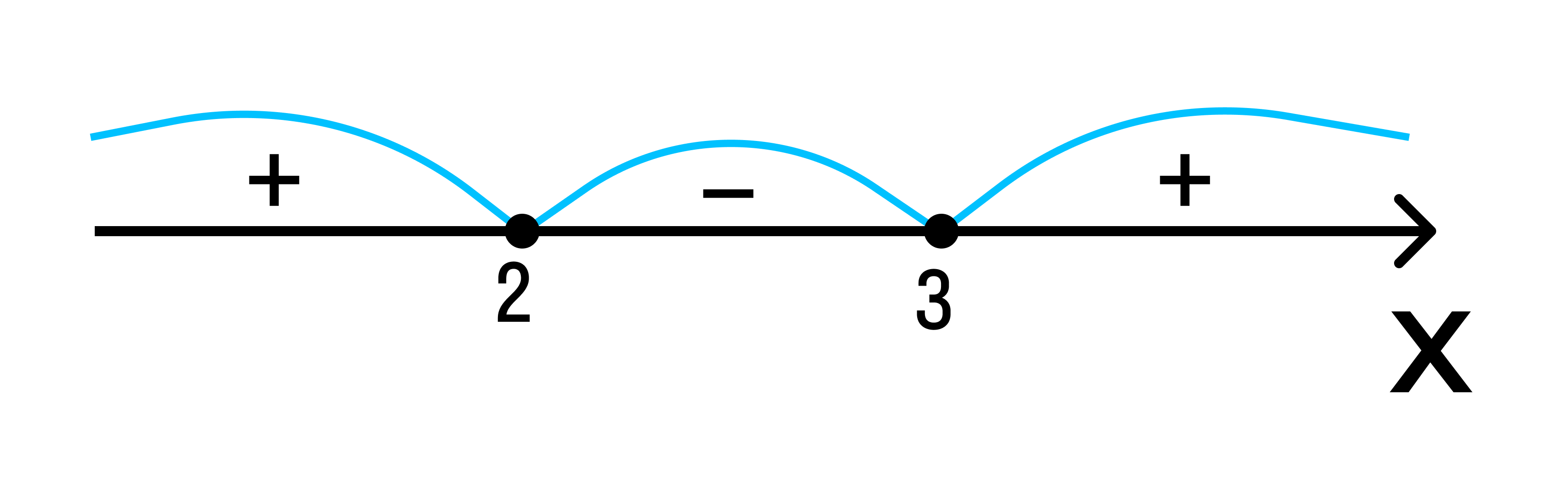
Отобразим эти данные на чертеже:
2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
- (25 — 3) (25 — 2) = 22*23 = 506 > 0
Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.
Исходное неравенство: (х — 3) * (х — 2) ≥ 0.
Если (х — 3) * (х — 2) > 0:
Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.
Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Ответ: х ≤ 0, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3
Источник
Конспект урока 9 класс на тему «Графическое решение неравенства с двумя переменными»
Конспект урока в 9 классе по алгебре
Графическое решение неравенства с двумя переменными
образовательные: рассмотреть графики неравенств с двумя переменными;
развивающие: способствовать развитию логического мышления, математической речи учащихся, внимания, памяти;
воспитательные: воспитание интереса к математике как учебному предмету через современные технологии преподавания; способствовать развитию навыков самоконтроля;
Оборудование: учебник, доска.
Тип урока: Урок изучения новых знаний.
Приветствие. Проверка готовности учеников к уроку.
Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
1. Сумма двух чисел равна 30, а их произведение равно 216. Найдите эти числа.
2. Гипотенуза прямоугольного треугольника равна 20 см, а его периметр равен 48 см. Найдите катеты треугольника.
1. Сумма двух чисел равна 40, а их произведение равно 364. Найдите эти числа.
2. Гипотенуза прямоугольного треугольника равна 25 см, а его периметр равен 60 см. Найдите катеты треугольника.
Учитель объявляет тему и цель урока.
Изучение нового материала
Часто приходится изображать на координатной плоскости множество решений неравенства с двумя переменными. Напомним, что решением неравенства с двумя переменными называют пару значений этих переменных, которая обращает данное неравенство в верное числовое неравенство.
Рассмотрим неравенство 3х 2 – 1/ y ≤ 8.
Пара значений переменных (-1; 1) обращает это неравенство в верное числовое неравенство 3 · (-1)2 – 1/1 ≤8, или 2 ≤ 8, и является решением неравенства. Пара значений (2; 1) приводит к неверному числовому неравенству 3 · 22 – 1/1 ≤ 8, или 11 ≤ 8, и не является решением данного неравенства.
На примерах рассмотрим, как изображается множество решений неравенства с двумя переменными на координатной плоскости.
Изобразим на координатной плоскости множество решений неравенства 2у + 3х ≤ 6.
Сначала построим прямую 2у + 3х = 6, или у = 3 – 3/2х. Она разбивает множество всех точек координатной плоскости на точки, расположенные выше ее, и точки, расположенные ниже ее. Возьмем из каждой области по контрольной точке, например A (1; 1) и B (1; 3).
Координаты точки А удовлетворяют данному неравенству 2у + 3х ≤ 6, т. е. 2 · 1 + 3 · 1 ≤ 6.
Координаты точки В не удовлетворяют данному неравенству 2 · 3 + 3 · 1 ≤ 6.
Так как данное неравенство может изменить знак на прямой 2у + 3х = 6, то неравенству удовлетворяет множество точек той области, где расположена точка А. Заштрихуем эту область.
Таким образом, мы изобразили множество решений неравенства 2у + 3х ≤ 6.
Изобразим множество решений неравенства х 2 + 2х + у 2 — 4у + 1 >0 на координатной плоскости.
Построим сначала график уравнения х 2 + 2х + у 2 — 4у + 1 = 0. Выделим в этом уравнении уравнение окружности: (х 2 + 2х + 1) + (у 2 — 4у + 4) = 4, или (х + 1) 2 + (у — 2) 2 = 22.
Это уравнение окружности с центром в точке O (-1; 2) и радиусом R = 2. Построим эту окружности.
Так как данное неравенство строгое и точки, лежащие на самой окружности, неравенству не удовлетворяют, то строим окружность.
Легко проверить, что координаты центра О окружности данному неравенству не удовлетворяют. Выражение х 2 + 2х + у 2 — 4у + 1 меняет свой знак на построенной окружности. Тогда неравенству удовлетворяют точки, расположенные вне окружности. Эти точки заштрихованы.
Изобразим на координатной плоскости множество решений неравенства (у — х 2 )(у — х — 3) ≤ 3.
Сначала построим график уравнения (у — х 2 )(у — х — 3) = 0. Им является парабола у = х 2 и прямая у = х + 3. Построим эти линии и отметим, что изменение знака выражения (у — х 2 )(у – х — 3) происходит только на этих линиях. Для точки А(0; 5) определим знак этого выражения: (5 — 0 2 )(5 — 0 — 3) > 0 (т. е. данное неравенство не выполняется). Теперь легко отметить множество точек, для которых данное неравенство выполнено (эти области заштрихованы).
Как видно из рассмотренных примеров, для построения множества решений неравенства с двумя переменными используется метод интервалов на координатной плоскости.
Задание на уроке
№ 482 (а, б); 483 (б, в); 484 (г); 485 (а); 486 (в); 487 (а, в); 488 (б); 489 (а); 490 (б); 491 (а); 492 (б).
№ 482 (в); 483 (а, г); 484 (в); 485 (б); 486 (г); 487 (б, г); 488 (а); 489 (б); 490 (а); 491 (б); 492 (а).
Какая была сегодня тема урока?
Какую цель ставили?
Расскажите по схеме, чему научились на уроке:
Источник