Применение графического метода решения задач при принятии управленческих решений
Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трехмерного простран6тва, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трех изобразить графически вообще невозможно.
Эти модели применяют для нахождения оптимального решения в ситуации распределения дефицитных ресурсов при наличии конкурирующих потребностей. Например, с помощью модели линейного программирования управляющий производством может определить оптимальную производственную программу, т.е. рассчитать, какое количество изделий каждого наименования следует производить для получения наибольшей прибыли при известных объемах материалов и деталей, фонде времени работы оборудования и рентабельности каждого типа изделия. Большая часть разработанных для практического применения оптимизационных моделей сводится к задачам линейного программирования.
Типичные варианты применения линейного программирования в управлении производством
Укрупненное планирование производства. Составление графиков производства, минимизирующих общие издержки с учетом издержек в связи с изменением ставки процента, заданных ограничений по трудовым ресурсам и уровням запасов.
Планирование ассортимента изделий. Определение оптимального ассортимента продукции, в котором каждому ее виду свойственны свои издержки и потребности в ресурсах (например, определение оптимальной структуры производства компонентов для бензина, красок, продуктов питания для человека, кормов для животных).
Маршрутизация производства изделия. Определение оптимального технологического маршрута изготовления изделия, которое должно быть последовательно пропущено через несколько обрабатывающих центров, причем каждая операция центра характеризуется своими издержками и производительностью.
Управление технологическим процессом. Сведение к минимуму выхода стружки при резке стали, отходов кожи или ткани в рулоне или полотнище.
Регулирование запасов. Определение оптимального сочетания продуктов на складе или в хранилище.
Календарное планирование производства. Составление календарных планов, минимизирующих издержки с учетом расходов на содержание запасов, оплату сверхурочной работы и заказов на стороне.
Планирование распределения продукции. Составление оптимального графика отгрузки с учетом распределения продукции между производственными предприятиями и складами, складами и магазинами розничной торговли.
Определение оптимального местоположения нового завода. Определение наилучшего пункта местоположения путем оценки затрат на транспортировку между альтернативными местами размещения нового завода и местами его снабжения и сбыта готовой продукции.
Календарное планирование транспорта Минимизация издержек подачи грузовиков под погрузку и транспортных судов к погрузочным причалам.
Распределение рабочих. Минимизация издержек при распределении рабочих по станкам и рабочим местам.
Перегрузка материалов. Минимизация издержек при маршрутизации движения средств перегрузки материалов (например, автопогрузчиков) между отделениями завода и доставке материалов с открытого склада к местам их переработки на грузовых автомобилях разной грузоподъемности с разными технико-экономическими характеристиками.
Графический (геометрический) способ решения ЗЛП обычно предполагает последовательное выполнение следующих действий:
1. Запись математических выражений, представляющих целевую функцию и ограничения, в виде равенств (уравнений).
2. Построение на графике прямых для уравнений, соответствующих ограничениям.
3. Определение области допустимых решений (ОДР) для задачи.
4. Построение на графике прямой, соответствующей целевой функции.
5. Параллельный перенос (перемещение) прямой, построенной для целевой функции, в одну из крайних точек ОДР для получения оптимального решения.
45. Возможные варианты графического метода решения задач при принятии управленческих решений
Пример 1.
Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем первой линии — 60 изделий, второй линии — 80 изделий. На радиоприемник первой модели расходуется 15 однотипных элементов электронных схем, на радиоприемник второй модели — 10 таких же элементов. Максимальный суточный запас используемых элементов равен 950 единиц. Прибыли от реализации одного радиоприемника первой и второй моделей равны 40$ и 20$ соответственно. Определите оптимальные суточные объемы производства первой и второй моделей на основе графического решения задачи.
1.Построение математической модели.
Переменные задачи
В задаче требуется установить, сколько радиоприемников первой и второй модели надо производить. Поэтому искомыми величинами задачи являются суточные объемы производства каждого типа радиоприемников:
– суточный объем производства радиоприемников первой модели, [шт/сутки];
– суточный объем производства радиоприемников второй модели, [шт/сутки];
Целевая функция
Цель задачи – добиться максимального дохода от реализации продукции. Т.е. критерием эффективности служит параметр суточного дохода, который должен стремиться к максимуму.Чтобы рассчитать величину суточного дохода от продажи радиоприемников обоих моделей, необходимо знать:
· их объемы производства, т.е. и радиоприемников в сутки;
· прибыль от их реализации – согласно условию, соответственно 40 и 20 $.
Таким образом, доход от продажи суточного объема производства радиоприемников первой модели равен 
$ в сутки, а от продажи радиоприемников второй модели – 
$ в сутки. Поэтому запишем ЦФ в виде суммы дохода от продажи радиоприемников первой и второй модели:
[$/сутки]
Ограничения
Возможные объемы производства радиоприемников и ограничиваются следующими условиями:
· количество элементов электронных схем, израсходованное в течении суток на производство радиоприемников обоих моделей, не может превышать суточного запаса этих элементов на складе;
· суточный объем первой технологической линии (производство радиоприемников первой модели) не может превышать 60 шт в сутки, второй (производство радиоприемников второй модели) – 80 шт;
· объемы производства радиоприемников не могут быть отрицательными.
Таким образом, все ограничения задачи делятся на 3 группы, обусловленные:
1) расходом элементов электронных схем;
2) суточным объемом технологических линий;
3)неотрицательностью объемов производства.
Запишем эти ограничения в математической форме:
1) Т.к. из условия на радиоприемники первой и второй модели необходимо 15 и 20 элементов соответственно, то данное ограничение имеет вид:
[шт/сутки]
2) Ограничения по суточному объему первой и второй технологических линий имеют вид:
[шт/сутки]
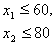
3) Неотрицательность объемов производства задается как
.
Таким образом, математическая модель этой задачи имеет вид
В ходе решения этой задачи графическим методом получили точку D(60;5) [шт/сутки].
Максимальное значение ЦФ равно 
[$/сутки].
Таким образом, наилучшим режимом работы предприятия является ежесуточное производство радиоприемников первой модели в количестве 60 штук и радиоприемников второй модели в количестве 5 штук. Доход от продажи составит 2500$ в сутки.
Решим графическим методом задачи использования сырья и составления рациона. Задача использования сырья. Для изготовления двух видов продукции Р 1 и Р 2 используют три вида сырья: S 1 , S 2 , S 3 . Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а так же величина прибыли, получаемая от реализации единицы продукции, приведены в таблице 1
| Вид сырья | Запас сырья | Количество единиц сырья, идущих на изготовление единицы продукции |
| Р 1 | Р 2 | |
| S 1 | ||
| S 2 | ||
| S 3 | ||
| Прибыль от единицы продукции, руб. |
Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.
Обозначим через х 1 количество единиц продукции Р 1 , а через х 2 – количество единиц продукции Р 2 . Получим систему ограничений:
которая показывает, что количество сырья, расходуемое на изготовление продукции, не может превысит имеющихся запасов.Конечную цель решаемой задачи – получение максимальной прибыли при реализации продукции – выразим как функцию двух переменных х 1 и х 2 . Реализация х 1 единиц продукции Р 1 и х 2 единиц продукции Р 2 дает соответственно 50х 1 и 40х 2 руб. прибыли, суммарная прибыль Z = 50х 1 + 40х 2 (руб.)
Оптимальный план задачи: х 1 = 90/23 = 3,9; х 2 = 40/23 = 1,7. Подставляя значения х 1 и х 2 в линейную функцию, получаем Z max = 50 3,9 + 40 1,7 = 260,3 Таким образом, для того чтобы получить максимальную прибыль в размере 260,3 руб., необходимо запланировать производство 3,9 ед. продукции Р 1 и 1,7 ед. продукции Р 2 .
Задача составления рациона. При откорме каждое животное ежедневно должно получать не менее 9 ед. питательного вещества S 1 , не менее 8 ед. вещества S 2 и не менее 12 ед. вещества S 3 . Для составления рациона используют два вида корма. Содержание количества единиц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма приведены в таблице 2
| Питательные вещества | Количество единиц питательных веществ в 1 кг корма. |
| Корм 1 | Корм 2 |
| S 1 | |
| S 2 | |
| S 3 | |
| Стоимость 1 кг корма, коп. |
Необходимо составить дневной рацион нужной питательности, причем затраты на него должны быть минимальными.
Решение. Для составления математической модели обозначим через х 1 и х 2 соответственно количество килограммов корма 1 и 2 в дневном рационе. Принимая во внимание значения, приведенные в таблице 2.2, и условие, что дневной рацион удовлетворяет требуемой питательности только в случае, если количество единиц питательных веществ не меньше предусмотренного, получаем систему ограничений
Если корм 1 не используется в рационе, то х 1 =0; в противном случае x 1 0. Аналогично имеем х 2 0. То есть должно выполняться условие неотрицательности переменных: х 1 0, х 2 0. Цель данной задачи – добиться минимальных затрат на дневной рацион, поэтому общую стоимость рациона можно выразить в виде линейной функции Z = 4х 1 + 6х 2 (коп.)
Имеем: х 1 = 2; х 2 = 3. Подставляя значения х 1 и х 2 в линейную функцию, получаем Z min = 4 2 + 6 3 = 26.
Таким образом, для того, чтобы обеспечить минимум затрат (26 коп. в день), необходимо дневной рацион составить из 2 кг корма 1 и 3 кг корма 2.
Источник
Графические методы в принятии управленческих решений. Дерево решений
Дерево решений — метод науки управления — схематичное представление проблемы принятия решений — используется для выбора наилучшего направления действий из имеющихся вариантов.
Метод дерева решений аналогичен методу сценариев с его эмоциональным содержанием, но предполагает аналитический подход к выбору наилучшего решения. Метод дерева решений позволяет руководителю визуально оценить результаты действий различных решений и выбрать наилучший их набор. Данный метод использует модель, разветвляющегося по каким — либо условиям процесса. Модель представляет собой графическое изображение связей основных и последующих вариантов управленческого решения. В ней приводятся решения и наименованиях управленческого решения, основных результатах каждого решения и ожидаемой эффективности.
Данный метод хорошо работает совместно с экспертными методами, так как некоторые этапы требуют оценки результатов специалистами. Реализация метода эффективна для типовых управленческих процессов, по которым накоплен значительный опыт и имеется документация о решениях, условиях их реализации и самих результатах.
Основные этапы реализации метода:
— составление новой цели развития или совершенствования компании;
— сбор материалов о реальном состоянии ел в компании по новой цели;
— формулирование проблемы как разности между новой целью и обобщённой ситуации в компании;
— выбор или разработка критериев оценки проблемы;
— декомпозиция проблемы на самостоятельные составные части;
— поиск ресурсов и исполнителей разрешения проблем;
— разработка вариантов основных решений и их предполагаемая эффективность;
— для каждого варианта основных решений разработка вариантов детализирующих решений;
— для каждого варианта детализирующего решения разработка вариантов очередного набора детализирующих решений;
— оценка каждой ветви взаимодействующих решений на эффективность действий и возможности достижения цели;
— выбор наиболее приемлемых сочетаний вариантов решений;
— практическая реализация выбранного варианта сочетания решений.
Графический метод дерева решений эффективен при аналитическом складе ума исполнителя, умеющего просчитывать несколько вариантов на несколько шагов вперед. Если результат очередного хода предполагается хорошим, то исполнитель задумывается над следующими вариантами шагом. Если предполагаемый результат его не устраивает, то исполнитель далее не развивает это направление шагов, а формирует новую цепочку. Данный метод основан на документальном представлении возможных вариантов разветвляющихся решений. Последовательности решений графически фиксируются на бумаге или на экране компьютера. Такое расположение решений напоминает дерево, на котором решения играют роль веток, а стволом является сам процесс выполнения всех решений. В теории управления существуют такие понятия как «дерево целей», «дерево функций» и «дерево структур». Метод дерева решений имеет приоритет наглядности над эмоциональной убедительностью метода сценариев. Наглядность часто служит основным мотивом при выборе варианта решения. Метод дерева решений позволяет руководителю визуально оценить результаты действия различных решений и выбрать наилучший их набор. Это очень эффектный метод. Он позволяет в случае тупикового варианта на каком-либо этапе отменить дальнейшую проработку всех решений, стоящих до него. Пример графической интерпретации метода приведен на рис.1.[1, с. 58]
Деревья решений — это метод, который пригоден не только для решения задач классификации, но и для вычислений и поэтому довольно широко применяется в области финансов и бизнеса, где чаще встречаются задачи численного прогноза. В результате применения этого метода к обучающей выборке данных создается иерархическая структура классифицирующих правил типа «ЕСЛИ. ТО. », имеющаявид дерева. Для того чтобы решить, к какому классу отнести некоторый объект или ситуацию, мы отвечаем на вопросы, стоящие в узлах этого дерева, начиная с его корня. Вопросы могут иметь вид «значение параметра A больше x?» для случая измеряемых переменных или вида «значение переменной В принадлежит подмножеству признаков С». Если ответ положительный, мы переходим к правому узлу следующего уровня, если отрицательный — то к левому узлу; затем снова отвечаем на вопрос, связанный с соответствующим узлом. Таким образом, мы, в конце концов, доходим до одного из оконечных узлов — листьев, где стоит указание, к какому классу (сочетанию признаков) надо отнести рассматриваемый объект. Этот метод хорош тем, что такое представлениеправил наглядно и его легко понять.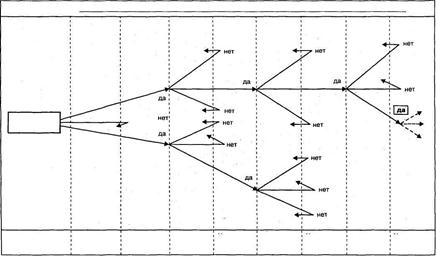 
( в общем виде)
Источник
