Теория игр. Матричные игры. Онлайн калькулятор
С помощю этого онлайн калькулятора можно решить задачу теории игр. Для решения задачи теории игр задайте количество строк и количество столбцов матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Предупреждение
Теория игр − теоретическая часть
Бывают ситуации, в которых сталкиваются интересы двух и более сторон. При этом эффективность принимаемого решения одной стороны зависит от действий другой стороны. Такие ситуации называются конфликтными. Конфликтная ситуация называется антагонистической, если увеличение выигрыша одной стороны на определенную величину приводит к уменьшению выигрыша другой стороны на такую же величину. Математическая модель таких ситуаций описывается матричной игрой. Участники игры (т.е. лица, принимающие решение) называются игроками. Принятие игроком того или иного решения в процессе игры и его реализация называется ходом. Ходы могут быть личными (т.е. сознательными) и случайными. Стратегия игрока − осознанный выбор одного из множества вариантов его действий. Стратегия называется чистой, если выбор игрока неизменен от партии к партии. У первого игрока есть m чистых стратегий, а у второго игрока n чистых стратегий. Если множество стратегий игроков конечный, то игра называется конечной, а если хотя бы у одного игрока множество стратегий бесконечно, то игра называется бесконечной. Стратегия игрока называется оптимальной, если она обеспечивает данному игроку (при многократном повторении) максимально возможный средний выигрыш или минимально возможный средний проигрыш.
Игры, в которых учавствуют 2 игрока, называются парными, а игры с большим числом участников − множественными. Если в парной игре выигрыш одной стороны точностью совпадает с проигрышем другой стороны, то игра называется игрой с нулевой суммой.
В зависимости от вида функций выигрышей, игры бывают матричные, биматричные, непрерывные, выпуклые и др.
Рассмотрим матричную игру двух участников с нулевой суммой и конечным числом возможных ходов.
Решение матричной игры в чистых стратегиях
Пусть игроки A и B распологают конечным числом возможных действий (чистых стратегий). Обозначим их через 
и 
, соответственно. Игрок A может выбрать чистую стратегию 
. В ответ на этот выбор, игрок B может выбрать чистую стратегию 
. Выбор стратегии 
первого игрока и ответный выбор стратегии 
игрока B единственным образом определяет результат aij выигрыш игрока A или проигрыш игрока B.
Таким образом игра с нулевой суммой однозначно определяется матрицей
 | (1) |
которая называется платежной матрицей или матрицей выигрышей. Строки матрицы (1) определяют стратегии первого игрока (), а столбцы соответствуют стратегиям второго игрока ().
Игра проходит партиями. Партия начинается с первого игрока. Он выбирает некоторую строку i матрицы. В ответ на это второй игрок выбирает некоторый столбец j. На этом заканчивается партия и второй игрок платит первому сумму aij, если aij>0 или первый игрок платит сумму aij второму игроку, если aij Теорема 1. В матричной игре нижняя цена игры не превосходит верхней цены, т.е. α ≤ β.
 . | (2) |
Если для чистых стратегий Ak и Bl игроков A и B имеет место равенство α = β, то пару чистых стратегий (Ak,Bl) называют седловой точкой матричной игры а γ=α = β чистой ценой игры. Элемент akl называют седловым элементом платежной матрицы.
Заметим, что отклонение игрока A от максимальной стратегии Ak ведет к уменьшению его выигрыша, а отклонение игрока B от минимальной стратегии Bl ведет к увеличению его проигрыша. Поэтому Ak и Bl являются оптимальными чистыми стратегиями игроков A и B, соответственно.
Тройку (Ak, Bl, γ) называют решением матричной игры. Если игра имеет седловую точку, то говорят, что она решается в чистых стратегиях.
Решение матричной игры в смешанных стратегиях
Если матричная игра не имеет седловой точки, то α ≠ β, и, Теорему 1, получим: α * и q * называются оптимальными, если они образуют седловую точку для платежной функции M(p,q), т.е.
 . |
Значение платежной функции при оптимальных смешанных стратегиях p * и q * называют ценой игры:
 . |
Теорема 2 (Основная теорема теории матричных игр). В любой матричной игре у игроков есть оптимальные смешанные стратегии.
Доказательство. Пусть игра имеет платежную матрицу
| , |
где все элементы положительны.
Пусть 
и 
− смешанные стратегии игроков A и B , соотвестстенно.
Математическое ожидание выигрыша игрока A равна:
 . |
При любом выборе игроками своих смешанных стратегий p и q, математическое ожидание будет положительным, так как все элементы aij платежной матрицы положительны, pi неотрицательные числа и среди них есть хотя бы одно положительное число, qj неотрицательные числа и среди них есть хотя бы одно положительное число.
Нижняя цена игры
 , |
так как aij >0, i=1,2. m, j=1,2. n. Поскольку α>0 и γ не может быть меньше нижней цены игры, то γ ≥ α, а так как α>0, то γ >0.
Пусть игрок A выбирает такую стратегию p, что математическое ожидание его выигрыша независимо от того, какую стратегию выбирает игрок B было не меньше некоторой величины γ:
 , | (3) |
где pi >0, i=1,2. m, 
. Каждая строка в системе линейных неравенств (3) соотвесттвует определенной стратегии игрока B.
Преобразуем систему нерравенств (3), введя новые обозначения:
 , |
Разделим все неравенства системы (3) на положительное число γ. Тогда имеем:
 , |
 , |
Цель игрока A − максимизировать свой гарантированный выигрыш γ или минимизировать величину
 . |
Таким образом, приходим к следующей задаче линейного программирования:
 , | (4a) |
 , | (4b) |
 . | (4c) |
Сделав аналогичные рассуждения с позиции игрока B, получим следующую задачу линейного программирования:
 , | (5a) |
 , | (5b) |
 . | (5c) |
Покажем, что задачи линейного программирования (4) и (5) имеют допустимые решения. Так как aij >0, то можно подобрать достаточно большие положительные числа yi, i=1,2. m так, чтобы выполнялись неравенства (4b). Значит задача линейного программирования (4) имеет допустимое решение.
Допустимое решение задачи линейного программирования (5) является нулевой вектор. Таким образом, пары двойственных задач линейного программирования (4) и (5) имеют допустимые решения. Тогда, согласно теории двойственных задач линейного программирования, обе эти задачи имеют оптимальные планы 
, 
, при этом оптимальные значения целевых функций данных задач равны:
 . |
Цена игры равна:
 . |
Найдем оптимальные смешанные стратегии игроков:
 , |
 . |
  , |
  . |
Пара 
образует седловую точку данной матричной игры в смешанных стратегиях.
Если в матрице 
есть отрицательные элементы или нули, то можно сделать матрицу положительным, добавив к каждому элементу матрицы достаточно большое положительное число r. Тогда получим следующую матрицу A’(aij+r).
Математическое ожидание выигрыша игрока A с платежной матрицей A(aij):
 |
Математическое ожидание игрока A с платежной матрицей A’(aij+r):
 |
   |
Игра с платежной матрицей A’ имеет седловую точку в смешанных стратегиях:
 |
Следовательно, игра с платежной матрицей A также имеет седловую точку в смешанных стратегиях а цена игры с платежной матрицей A равна:
 . |
Для рассмотрения численного примера матричной игры, введите в калькуляторе в начале страницы элементы матрицы и нажмите на кнопку вычислить. Онлайн калькулятор выдаст подробное рашение задачи.
Источник
Графическое решение матричной игры
Если число стратегий одного из игроков равно двум, то для нахождения оптимальных стратегий можно легко воспользоваться графическим методом.
Пусть платежная матрица имеет вид
.
Для произвольной стратегии второго игрока, контролирующего столбцы, имеем выигрыш первого игрока
,
поскольку, как сказано раньше,
, 
.
Графиком зависимости 
будет некоторая прямая. Для разных стратегий, то есть для разных 
, получаются разные прямые.
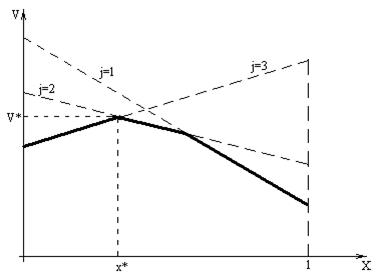
Рассмотрим прямоугольную систему координат, где по оси абсцисс откладывается единичный отрезок A1A2; точка A1 изображает стратегию A1 , а точка A2 изображает стратегию A2. Все промежуточные точки этого отрезка — смешанные стратегии первого игрока, причем расстояние до правого конца отрезка — это вероятность p1 стратегии A1, расстояние до левого конца отрезка это вероятность p2 стратегии A2. На перпендикулярах х=0 и х=1 откладываем выигрыши при стратегиях A1 и A2 соответственно (Рис.3.1).
Рис. 3.1. Графическое нахождение цены игры
На рис. 3.1 изображен случай 
для игры 2 
3. Из принципа минимакса следует, что надо взять нижнюю огибающую всех прямых, соответствующих стратегиям второго игрока (она показана на рисунке жирной линией), а на этой ломаной, обязательно обращенной выпуклостью вверх, надо найти вершину, имеющую максимальное значение v*. Абсцисса этой точки x* и будет искомым значением p1*.
Геометрически можно определять и оптимальную стратегию игрока В для игры 
, но в этом случае строится не нижняя, а верхняя граница выигрыша и на ней определяется не максимум, а минимум.
Алгоритм геометрического решения игры 2×N
1. Откладываем горизонтальный отрезок [0,1], каждая точка которого соответствует смешанной стратегии игрока A. В концах этого отрезка проводим два перпендикуляра. Левый соответствует чистой стратегии A1, правый — чистой стратегии A2 игрока A.
2. На левом перпендикуляре от точки 0 его пересечения с горизонтальным отрезком откладываем (как на вертикальной числовой оси) все элементы первой строки платежной матрицы. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) все элементы второй строки платежной матрицы. При этом масштабы на обоих перпендикулярах должны быть одинаковые, но не обязаны совпадать с масштабом отрезка [0,1].
3. Каждую пару точек, изображающих элементы a1j, a2j, j=1. n, стоящих в j-м столбце платежной матрицы, соединяем отрезком a1j, a2j . Таким образом будут построены n отрезков, представляющих собой графики n линейных функций
4. Находим нижнюю огибающую семейства построенных отрезков a1j, a2j, представляющую собой выпуклую вверх ломаную. Затем находим максимальную точку нижней огибающей. Абсцисса р o этой точки определяет оптимальную смешанную стратегию P o =(1- p o , p o ) игрока A. Ордината наивысшей точки нижней огибающей равна цене игры V.
5. Верхний из концов нижней огибающей, лежащих на перпендикулярах, есть нижняя цена игры в чистых стратегиях, т.е. a.Нижний из верхних концов отрезковa1j, a2j, j=1. n, есть верхняя цена игры в чистых стратегиях b.
6. Элемент платежной матрицы, изображающая точка которого является нижней на перпендикуляре, где она лежит, и верхним концом отрезка, на котором она лежит, будет седловой точкой игры. В этом случае чистая стратегия игрока B, номер которой совпадает со вторым индексом седловой точки, является оптимальной.
Пример 4. Графически решить игру: 
Действуя по алгоритму геометрического нахождения игры 2×N (рисунок 3.2), находим, что цена игры V=3,5, нижняя цена игры: a=2, верхняя цена игры: b=4, оптимальная стратегия игрока A: P o =(1/2,1/2).
Алгоритм геометрического решения игры М×2
1. Откладываем горизонтальный отрезок [0,1], каждая точка которого
соответствует смешанной стратегии игрока B. В концах этого отрезка проводим два перпендикуляра. Левый соответствует чистой стратегии B1, правый — чистой стратегии B2игрока B.
2. На левом перпендикуляре от точки 0 его пересечения с горизонтальным отрезком откладываем (как на вертикальной числовой оси) все элементы первого столбца платежной матрицы. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) все элементы второго столбца платежной матрицы. При этом масштабы на обоих перпендикулярах должны быть одинаковые, но не обязательно совпадающие с масштабом отрезка [0,1].
3. Каждую пару точек, изображающих элементы ai1, ai2, i=1. m, стоящих в i-той строке платежной матрицы, соединяем отрезком ai1, ai2 . Таким образом будут построены m отрезков, представляющих собой графики m линейных функций, зависящих от вероятности q: H(Ai,Q)=(ai2-ai1)q+ai1, i=1. m, q Î[0,1].
4. Находим верхнюю огибающую семейства построенных отрезков ai1, ai2 , представляющую собой выпуклую вниз ломаную. Затем находим минимальную точку верхней огибающей. Абсцисса q o этой точки определяет оптимальную смешанную стратегию Q o =(1-q o ,q o ) игрока B. Ордината наинизшей точки верхней огибающей равна цене игры V.
5. Верхний из нижних концов отрезков ai1, ai2 есть нижняя цена игры в чистых стратегиях, т.е. a. Нижний из концов верхней огибающей (лежащих на перпендикулярах) есть верхняя цена игры в чистых стратегиях, т.е. b.
6. Элемент платежной матрицы, изображающая точка которого является нижним концом отрезка, на котором она лежит, и верхней на перпендикуляре,на котором она лежит, будет седловой точкой игры. В этом случае чистая стратегия игрока A, номер которой совпадает с первым индексом седловой точки, является оптимальной.
Пример 5. Графически решить игру: 
Действуя по алгоритму геометрического нахождения игры М×2
(рисунок 3.3), находим, что цена игры V=4, нижняя цена игры: a=3, верхняя цена игры: b=5, оптимальная стратегия игрока B: Q o =(2/3, 1/3).
Пример 9. Решить графически игру, заданную платежной матрицей: 
Нижняя цена игры равна а11=1,5. Верхняя цена игры равна а21=2, седловая точка отсутствует.
Для игрока А решение представлено на рис. 3.4. Точка N определяет оптимальную стратегию, а ордината — цену игры v. Найдем точку пересечения соответствующих прямых:
Рис. 3.4. Решение матричной игры для игрока А
Следовательно, оптимальная стратегия игрока А заключается в выборе стратегии А1 с вероятностью 0,6 и стратегии А2 с вероятностью 0,4. При этом цена игры v = 1,8.
Для игрока В решение представлено на рис. 3.5. Находя точку пересечения соответствующих прямых, получаем М(0,2; 1,8).
Рис. 3.5. Решение матричной игры для игрока В
Следовательно, оптимальная стратегия игрока В заключается в выборе стратегии В1 с вероятностью 0,8 и стратегии В2 с вероятностью
0,2 = 1 – 0,8. При этом цена игры v = 1,8.
Оптимальное решение игры найдено.
Пример 10. Найти решение игры, заданной матрицей
Проверим наличие седловой точки
Так как 
, седловой точки нет. Решим матричную игру графически. Построим прямые, соответствующие стратегиям игрока А.
Ломанная 
изображает верхнюю границу выигрыша игрока А. На нем определяем К с минимальной ординатой, которая и есть цена игры 
. Оптимальные стратегии для игрока А – вторая и третья.
Матрица оптимальных стратегий имеет вид
, 
,
, 
,
, 
,
, 
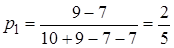
Следовательно, решение игры таково:
, 
, 
Пример 11. Решить матричную игру
Решение. Проверим наличие седловой точки
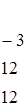
Здесь 
– седловой точки нет.
Решим матричную игру графически. Построим прямые, соответствующие стратегиям игрока В.
Ломаная 
соответствует нижней границе выигрыша. На ней определяем точку К с максимальной ординатой, которая и есть цена игры 
. Оптимальные стратегии для игрока В – первая и четвертая.
Матрица оптимальных стратегий имеет вид
, 
,
, 
,
, 
, 
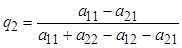
При этом 
ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования.
ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между.
ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры.
Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Источник
