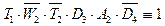Графический способ решения логических задач это

Решение логических задач на ЭВМ.

Графический способ решения логической задачи.

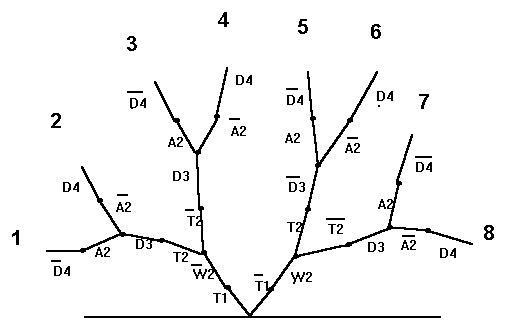
Графический способ решения логических задач заключается в вычерчивании «дерева логических условий». «Дерево» выражает в виде простого чертежа логическую взаимосвязь между данными высказываниями. Каждому простому высказыванию (с отрицанием или без) на дереве соответствует одна ветвь.Логической сумме (дизъюнкции) на логическом дереве соответствует «разветвление» ветвей, логическому произведению (конъюнкция) — «следование» ветвей друг за другом.

Для вычерчивания графического дерева задачи №1 обратимся к высказываниям болельщиков (или можно воспользоваться уравнениями (1),(2), (3)).

Рис.6.

Проанализируем каждую ветвь. Для этого для каждой пронумерованной ветви выписываем формулу. Каждая ветвь состоит из последовательно соединенных частей, что соответствует логической операции конъюнкция.

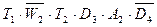
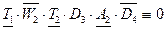
Ветвь 1: . Полученная формула принимает ложное значение , т.к. T₁×T₂º0, A₂×T₂º0

Ветвь 2: 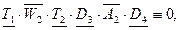т.к. T₁×T₂º0, D₃×D₄ º0

Ветвь 3:

Ветвь 4: 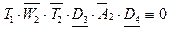, т.к. D₃×D₄ º0

Ветвь 5: 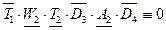, т.к. W₂×T₂º0, T₂×A₂º0, W₂×A₂º0

Ветвь 6: 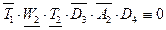, т.к. W₂×T₂º0

Ветвь 7: 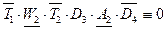, т.к. W₂×A₂º0

Ветвь 8: 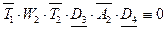, т.к. D₃×D₄ º0

Итак, только выражение ветви 3 эквивалентно 1:

Из этого выражения следует: Таня — первая; Алла — вторая; Даша — третья; Валя — четвертая.

Решение логических задач на ЭВМ.

Решить задачу на ЭВМ, значит найти истинное логическое выражение, отвечающее на поставленный в задаче вопрос. Чтобы это выполнить, необходимо перебрать все возможные значения T₁, W₂ , T₂, D₃, A₂, D₄ и выбрать истинное значение основной функции (F), которая равна логическому произведению уравнений (1)-(8).

Учитывая, что каждое простое высказывание (T₁, W₂ , T₂, D₃, A₂, D₄) может принимать только два значения истина (1) и ложь (0), то в алгоритме и программе будут использованы вложенные циклы с параметром (начальное значение параметра цикла равно 0, конечное – 1). По правилам алгоритмического языка записываются выражения (1)-(8). В случае, если F принимает значение 1 (истина), то мы выводим на экран сообщение о том, какие значения принимают T1, W2, T2, D3, A2, D4.

Источник

Как решать логические и математические задачи

Решение задач на логику — отличная гимнастика для ума детей и взрослых на каждый день. На ЛогикЛайк более 3500 заданий с ответами и пояснениями, полноценный учебный комплекс для развития логики и способностей к математике.

Решаем логические задачи

Чтобы научиться решать типовые логические задачи, простые и нестандартные математические задачи, важно знать основные приемы и методы их решения. Ведь решить одну и ту же задачу и прийти к правильному ответу во многих случаях можно разными способами.

Знание и понимание различных методов решения поможет определить, какой способ подойдет лучше в каждом конкретном случае, чтобы выбрать наиболее быстрый и простой путь получения ответа.

К «классическим» логическим задачам относятся текстовые задачи, цель решения которых состоит в распознавании объектов или расположении их в определенном порядке в соответствии с заданными условиями.

Более сложными и увлекательными типами заданий являются задачи, в которых отдельные утверждения являются истинными, а другие ложными. Задачи на перемещение, перекладывание, взвешивание, переливание — самые яркие примеры широкого ряда нестандартных задач на логику.

Основные методы решения логических задач

• метод рассуждений;
• с помощью таблиц истинности;
• метод блок-схем;
• средствами алгебры логики (алгебры высказываний);
• графический (в том числе, «дерево логических условий», метод кругов Эйлера);
• метод математического бильярда.

Давайте рассмотрим подробнее с примерами три популярных способа решения логических задач, которые мы рекомендуем использовать в начальной школе (детям 6-12 лет):

• метод последовательных рассуждений;
• разновидность метода рассуждений — «с конца»;
• табличный способ.

Метод последовательных рассуждений

Самый простой способ решения несложных задач заключается в последовательных рассуждениях с использованием всех известных условий. Выводы из утверждений, являющихся условиями задачи, постепенно приводят к ответу на поставленный вопрос.

На столе лежат Голубой , Зеленый , Коричневый и Оранжевый карандаши.

Третьим лежит карандаш, в имени которого больше всего букв. Голубой карандаш лежит между Коричневым и Оранжевым .

Разложи карандаши в описанном порядке.

Рассуждаем. Последовательно используем условия задачи для формулирования выводов о позиции, на которой должен лежать каждый следующий карандаш.

• Больше всего букв в слове «коричневый», значит, он лежит третьим.
• Известно, что голубой карандаш лежит между коричневым и оранжевым. Справа от коричневого есть только одна позиция, значит, расположить голубой между коричневым и другим карандашом возможно только слева от коричневого.
• Следующий вывод на основе предыдущего: голубой карандаш лежит на второй позиции, а оранжевый — на первой.
• Для зеленого карандаша осталась последняя позиция — он лежит четвертым.

Метод «с конца»

Такой способ решения является разновидностью метода рассуждений и отлично подходит для задач, в которых нам известен результат совершения определенных действий, а вопрос состоит в восстановлении первоначальной картины.

Бабушка испекла для троих внуков рогалики и оставила их на столе. Коля забежал перекусить первым. Сосчитал все рогалики, взял свою долю и убежал.
Аня зашла в дом позже. Она не знала, что Коля уже взял рогалики, сосчитала их и, разделив на троих, взяла свою долю.
Третьим пришел Гена, который тоже разделил остаток выпечки на троих и взял свою долю.
На столе осталось 8 рогаликов.

Сколько рогаликов из восьми оставшихся должен съесть каждый, чтобы в результате все съели поровну?

Начинаем рассуждение «с конца».
Гена оставил для Ани и Коли 8 рогаликов (каждому по 4). Получается, и сам он съел 4 рогалика: 8 + 4 = 12.
Аня оставила для братьев 12 рогаликов (каждому по 6). Значит, и сама она съела 6 штук: 12 + 6 = 18.
Коля оставил ребятам 18 рогаликов. Значит, сам съел 9: 18 + 9 = 27.

Бабушка положила на стол 27 рогаликов, рассчитывая, что каждому достанется по 9 штук. Поскольку Коля уже съел свою долю, Аня должна съесть 3, а Гена — 5 рогаликов.

Решение логических задач с помощью таблиц истинности

Суть метода состоит в фиксации условий задачи и полученных результатов рассуждений в специально составленных под задачу таблицах. В зависимости от того, является высказывание истинным или ложным, соответствующие ячейки таблицы заполняются знаками «+» и «-» либо «1» и «0».

Три спортсмена ( красный , синий и зеленый ) играли в баскетбол.
Когда мяч оказался в корзине, красный воскликнул: «Мяч забросил синий».
Синий возразил: «Мяч забросил зеленый».
Зеленый сказал: «Я не забрасывал».

Кто забросил мяч, если только один из троих сказал неправду?

Сначала таблицу составляют: слева записывают все утверждения, которые содержатся в условии, а сверху — возможные варианты ответа.

Затем таблицу последовательно заполняют: верные утверждения отмечают знаком «+», а ложные утверждения — знаком «-«.

Рассмотрим первый вариант ответа («мяч забросил красный «), проанализируем утверждения, записанные слева, и заполним первый столбик.
Исходя из нашего предположения («мяч забросил красный «), утверждение «мяч забросил синий» — ложь. Ставим в ячейке «-«.
Утверждение «мяч забросил зеленый» также ложь. Заполняем ячейку знаком «-«.
Утверждение зеленого «Я не забрасывал» – истина. Ставим в ячейке «+».

Рассмотрим второй вариант ответа (предположим, что мяч забросил зеленый ) и заполним второй столбик.
Утверждение «мяч забросил Синий» — ложь. Ставим в ячейке «-«.
Утверждение «мяч забросил зеленый « — истина. Заполняем ячейку знаком «+».
Утверждение зеленого «Я не забрасывал» – ложь. Ставим в ячейке «-«.

И, наконец, третий вариант: предположим, что «мяч забросил синий «.
Тогда утверждение «мяч забросил синий « — истина. Ставим в ячейке «+».
Утверждение «мяч забросил зеленый» — ложь. Заполняем ячейку знаком «-«. Утверждение зеленого «Я не забрасывал» – истина. Ставим в ячейке «+».

Так как по условию лишь один из троих ребят сказал неправду, в заполненной таблице выбираем такой вариант ответа, где будет только одно ложное утверждение (в столбце один знак «-«). Подходит третий столбец.

Значит, правильный ответ – мяч забросил синий.

Метод блок-схем

Метод блок-схем считается оптимальным вариантом для решения задач на взвешивание и на переливание жидкостей. Альтернативный способ решения этого типа задач — метод перебора вариантов — не всегда является оптимальным, да и назвать его системным довольно сложно.

• графически (блок-схемой) описываем последовательность выполнения операций;
• определяем порядок их выполнения;
• в таблице фиксируем текущие состояния.

Подробнее об этом и других способах решения логических задач с примерами и описанием хода решения мы рассказываем в полном Курсе ЛогикЛайк по развитию логического мышления.

Отгадывайте самые интересные загадки на логику, собранные специально для постоянных читателей нашего блога и учеников LogicLike, решайте логические задачи онлайн вместе с тысячами детей и взрослых!

Учим детей 5-12 лет решать любые логические и математические задачи. Более 3500 занимательных заданий с ответами и пояснениями.

Источник

Графический способ решения логических задач

Графический способ решения логических задач

Если в задаче фигурирует не два, а больше мно­жеств, то ее решение с помощью таблицы может за­метно усложниться, в этом случае приходится пользо­ваться несколькими таблицами. Рассмотрим графичес­кий способ решения задач. Договоримся элементы множеств изображать точками плоскости. Если по ус­ловию задачи между двумя элементами этих множеств есть соответствие, то будем соединять такие элементы сплошной линией. Если же между двумя элементами множеств соответствия нет, то будет соединять их пун­ктирной линией. При наличии взаимно однозначного соответствия каждый элемент одного из множеств бу­дет соединяться сплошной линией только с одним эле­ментом другого множества, а с остальными элемента­ми он будет соединяться пунктирными линиями.

Задача 1. У трех подружек — Ксюши, Насти и Оли — новогодние карнавальные костюмы белого, синего и фиолетового цветов, и шапочки тех же цве­тов. У Насти цвет костюма и шапочки совпали, у Ксюши ни костюм, ни шапочка не были фиолетового цвета, а Оля была в белой шапочке, но цвет костюма у нее не был белым. Как были одеты девочки?

Множество костюмов Множество шапочек.

Будет изображать множество подружек, шапочек и костюмов кругами, а элементы множеств — точками, помещенными в эти круги.

Костюм и шапочка Насти одного цвета. Костюм и шапочка Ксюши не фиолетового цвета. Оля в белой шапочке. Костюм у Оли не белый.

Из условия (2) ясно, что костюм и шапочка Ксюши не фиолетовые, поэтому соединяем элементы множеств — и — пунктирными линиями. Из условия (3) — Оля в белой шапочке, поэтому соединя­ем сплошной линией элементы множества — . Из условия (4) — у Оли костюм не белый, поэтому соединяем пунктирной линией элемен­ты множеств — .Видим, что Ксюша не в фиолетовой шапочке и не в белой (в белой — Оля), значит, Ксюша в синей шапочке. Соединяем сплошной линией элементы мно­жеств — . Так как в бе­лой шапочке Оля, в синей шапочке Ксюша, то сплош­ной линией следует соединить элементы множеств — . Итак, Настя в фиолетовой шапочке. По условию (1) костюм и ша­почка у Насти одного цвета, поэтому соединяем сплош­ной линией элементы множеств — фиоле­товый костюм>

Теперь видно, что Оля в синем костюме: она не в белом (условие 4) и не в фиолетовом (в фиолетовом костюме Настя), а Ксюша в белом костюме.

Таким образом, Настя в фиолетовом костюме и шапочке, Ксюша в синей шапочке и белом костюме, а Оля в синем костюме и белой шапочке.

Задача 2. Три друга — Алеша, Сергей и Денис — купили щенков разной породы: щенка ротвейлера, щенка колли и щенка овчарки. Известно, что: щенок Алеши темнее по окрасу, чем ротвейлер, Лесси и Гриф; щенок Сергея старше Грифа, ротвейлера и овчарки; Джек и ротвейлер всегда гуляют вместе. У кого ка­кой породы щенок? Назовите клички щенков.

Решение. Заметим, что соответствие взаимно од­нозначное.

Выделяем ключевые условия.

Щенок Алеши не ротвейлер, его зовут не Лес­си и не Гриф, так как по условию

задачи он темнее по окрасу, чем ротвейлер, Лесси и Гриф.

Щенка Сергея зовут не Гриф, это не ротвейлер и не овчарка. Ротвейлера зовут не Джек.

В данной задаче следует рассматривать на плоско­сти три множества: множество мальчиков, множество кличек и множество пород собак. Каждое из множеств

содержит три элемента.

Так как щенок Алеши не ротвейлер, его зовут не Лесси и не Гриф (условие 1), то следует соединить пунктирными линиями элементы множеств — , — , — . Как видно, щенка Алеши зовут не Лесси и не Гриф, следовательно, его зовут Джек. Со­единяем соответствующие элементы сплошной лини­ей. Так как щенка Сергея зовут не Гриф, он не ротвейлер и не, овчарка (2), соединяем пунктирными линиями элементы множеств — , — , — .

Множество пород собак Множество кличек собак

Теперь видно, что у Сергея щенок породы колли. Соединяем соответствующие элементы сплошной ли­нией. Кличка щенка Сергея не Гриф (2) и не Джек (мы уже знаем, что Джеком зовут щенка Алеши), значит, сплошной линией соединяем элементы мно­жеств — , то есть щенка Сергея зовут Лесси. Очевидно, что щенка Дениса зовут Гриф. Так как у Алеши не ротвейлер (1) и не колли (колли у Сергея), значит, у Алеши овчарка. Понятно, что в этом случае ротвейлер у Дениса.

Задача 3. Три друга — Алеша, Боря и Володя — учатся в различных школах Санкт-Петербурга (в школах № 000, 141 и 164). Все они живут на различ­ных проспектах (проспект Энтузиастов, проспект Наставников, проспект Косыгина). Причем один из них любит математику, второй — биологию, а тре­тий — химию. Известно, что:

Алеша не живет на проспекте Энтузиастов, а Борис не живет на

мальчик, живущий на проспекте Энтузиастов, не учится в школе №

мальчик, живущий на проспекте Наставников, учится в школе № 000

и любит математику;

Володя учится в школе № 000; ученик школы № 000 не любит химию.

В какой школе учится каждый из друзей, на ка­ком проспекте он живет и какой предмет любит?

Решение. Здесь следует рассмотреть четыре мно­жества: множество друзей, множество проспектов, множество школ и множество школьных предметов. Каждое из множеств содержит три элемента.

Из условия (1): Алеша не живет на проспекте Эн­тузиастов, а Борис не живет на проспекте Наставни­ков. Соединяем пунктирными линиями элементы множеств — , — . Из условия (2) ясно, что мальчик, живущий на проспекте Энтузиастов, не учится в школе № 000, поэтому соединяет пунктир­ной линией элементы множеств — . Из условия (3) ясно, что мальчик, живущий на проспекте Наставников, учит­ся в школе № 000 и любит математику, поэтому со­единяем сплошными линиями элементы множеств: — , — , — . Из условия (4) — Володя учится в школе № 000. Соединяем сплошной линией элементы множеств — . Из условия (5) — ученик школы № 000 не любит хи­мию. Соединяем пунктирной линией элементы мно­жеств — .

Теперь видно, что ученик школы № 000 любит биологию (он не любит химию по условию и не любит математику — этот предмет любит ученик школы № 000). Соединяем сплошной линией элементы мно­жеств — . Очевидно, что ученик школы № 000 любит химию. Соединяем сплошной линией соответствующие элементы. Заме­чаем, что ученик школы № 000 живет на проспекте Косыгина (по условию 2 он не живет на проспекте Энтузиастов и не живет на проспекте Наставников, так как там живет ученик школы № 000 — условие 3). Соединяем сплошной линией элементы множеств — . Очевидно, что ученик школы № 000 живет на проспекте Энту­зиастов, и, значит, соответствующие элементы мож­но соединить сплошной линией.

Множество друзей Множество проспектов

Множество школ Множество школьных предметов

Теперь видно, что ученика школы № 000 зовут Володя, он живет на проспекте Косыгина и любит химию. Соединяем сплошной линией элементы множеств — , — . Так как Алеша не живет на проспекте Энтузиастов и не живет на проспекте Ко­сыгина, то, значит, он живет на проспекте Наставни­ков и, значит, учится в школе № 000 и любит мате­матику. Становится очевидным, что Боря живет на проспекте Энтузиастов, учится в школе № 000 и лю­бит биологию.

Источник