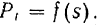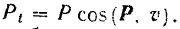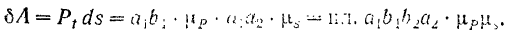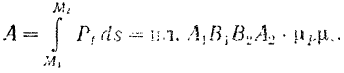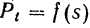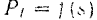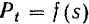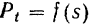Графический способ расчета работы

Графический способ вычисления работы

Графический способ вычисления работы

Вычисление работы си ты на конечном пути по установленным формулам, без знания закона движения точки приложения силы, возможно лишь в частных случаях (например, при постоянной силе).

Для вычисления же работы силы в общем случае, когда сила может зависеть от времени, координат и скорости, нужно знать закон движения точки приложения силы. Только в этом случае можно выразить, как мы видели при решении задачи 86, все переменные в функции времени 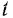и вычислить соответствующий интеграл.

Если же закон движения точки приложения силы неизвестен, то для вычисления работы силы нужно сначала найти этот закон, т. е. решить вторую основную задачу динамики.

На практике для определения работы часто пользуются графическим способом, используя для этой цели график зависимости

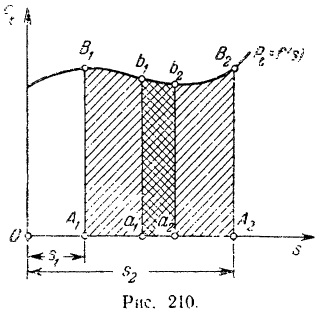
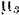
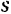
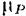
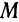
По оси абсцисс этого графика (рис. 210) отложены, в некотором масштабе значения дуговой координаты точки приложения силы, а по оси ординат, также в каком-то масштабе , соответствующие им значения проекции этой силы на направление скорости точки , т.е.

Элементарная работа силы будет равна

Работа силы на конечном перемещении ее точки приложения из положения с дуговой координатой в положение с координатой будет выражаться в некотором масштабе площадью фигуры (рис. 210):

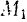
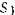
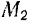
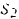
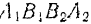
Работа силы на некотором перемещении ее точки приложения выражается в определенном масштабе площадью фигуры, ограниченной осою абсцисс, кривой

и двумя ординатами, соответствующими начальному и конечному положениям точки приложение силы.

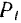
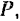
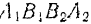
На рис. 210 алгебраические значения касательной составляющей силы отложены и положительную сторону соответствующей оси и потому работа силы изображаемая площадью фигуры , будет положительной. Если же построенная кривая

будет расположена от оси абсцисс в сторону отрицательных значений 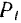, то соответствующая площадь будет изображать отрицательную работу.

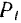
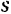
К графическому способу определения работы силы приходится прибегать в тех случаях, когда нам известны значения силы только для отдельных значении , установление же аналитической зависимости

затруднительно или даже невозможно. В ряде случаев (например, при определении работы пара или газа в цилиндрах паровой машины или двигателя) график зависимости

получается автоматически, при помощи самопишущих приборов, называемых индикаторами.

В заключение отметим следующее обстоятельство.

Хотя установленное в механике понятие работы (называемой иногда механической работой) и возникло из повседневного опыта, но оно не всегда совпадает с тем, что понимают под работой с физиологический точки зрения. Так, человек, неподвижно держащий па вытянутых руках тяжелый груз, не совершает, очевидно, с точки зрения механики, никакой работы (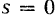). С физиологической же точки зрения он совершает, конечно, определенную работу.

Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:

Возможно вам будут полезны эти дополнительные темы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Графический метод расчета параметров сетевого графика

Рассчитать параметры сетевой модели графическим (секторным) методом можно через калькулятор.

Помимо него существуют следующие способы расчета: табличный метод, метод потенциалов.

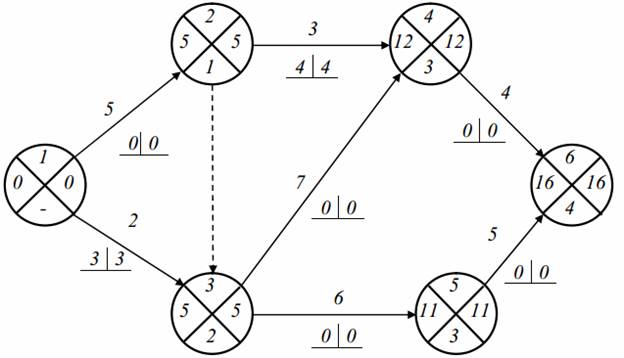
Пример . Определим параметры для событий и критический путь на графике. На практике получил широкое распространение четырехсекторный способ расчета ранних и поздних сроков свершения событий. При этом способе кружок сетевого графика, обозначающий событие, делится на четыре сектора (рис. 2, а). В верхнем ставится номер события i, в левом – наиболее раннее из возможных время свершения события t_p(i), в правом – наиболее позднее из допустимых время свершения события t_п(i), в нижнем – резерв времени данного события R(i).

Раннее время свершения события t_p(i) определяется продолжительностью максимального пути max(t) до (i), предшествующего событию i: t_p(i)=max(t) до (i).
Послойно, переходя от исходного события до конечного, определим t_p(i). Всегда для начального события t_p(1)=0.
Для события 3 (рис., б) – t_p(3)=max<1+3,0+5>=5; для события 4 – t_p(4)=max<1+2,5+6>=11.
Длина критического пути L_кр=11. Послойно, переходя от конечного события до начального, определим t_п(i). Всегда для конечного события t_п(4)=t(L_кр)=11. Позднее время свершения события t_п(i) определяется временем достаточным для выполнения работ, следующих за этим событием, т.е. зная продолжительность максимального из последующих за событием i путей max(t) после (i) и продолжительность критического пути t(L_кр), можно найти t_п(i)= t(L_кр)-max(t) после (i).
Для события 2 – t_п(3)=11-max<3+6,2>=2.
Для критического пути время раннего свершения события t_p(i) равно времени позднего свершения этого события t_п(i), т.е. t_p(i)= t_п(i). Зная ранние и поздние сроки свершения событий сетевого графика, легко выявить резерв времени каждого из них R(i)= t_п(i)- t_p(i).
Резерв времени события показывает максимально допустимое время, на которое можно отодвинуть момент его свершения, не вызывая увеличения критического пути. События критического пути резерва времени не имеют.
Связь параметров сетевого графика для событий и работ показана в таблице.

Источник

Графический способ расчета

Графический способ расчета

Аналитический способ расчета поставов предусматривает проведение множества вычислений, точный, но достаточно трудоемким. При графическом способе применяют график-квадрант (рис. 34).

На оси абсцисс графика отложено двойное расстояние от центра торца бревна к пласти доски, т. е. расстояние между симметричными пропилами. На оси ординат слева – ширина досок с припуском на усушку, по вертикальной шкале справа можно определять оптимальную ширину досок, которые выпиливают из параболической зоны.

Рис. 34. График квадрант для расчета поставов

На график нанесены: а) четверти концентрических окружностей диаметром от 10 до 50 см, которые построены по уравнению
b2 = d2 – Е2; б) наклонная прямая линия с пометкой «квадратный брус», построенная по формуле b = Е = 0,707d (по этой линии можно определить ширину боковой пласти квадратного бруса); в) несколько наклонных линий с пометкой K, равной 1,1; 1,2; 1,3 и 1,4, которые построены по формуле . По этим линиям можно определить Екр в зависимости от d и K = D / d. Рассмотрим порядок расчета поставов по графику-квадранту на примере.

Пример 5. Хвойные бревна диаметрам 24 см и длиной 5 м распиливают с брусовкой по поставу I – ; II – на обрезные доски. Ширина пропила составляет 3,6 мм. Выполнить расчет постава графическим способом.

Решение. Сначала сделаем дополнительные вычисления. Определим комлевый диаметр бревна D = d + cL = 24 + 0,86 • 5 = 28,3 см и коэффициент сбега K = D / d = 28,3 / 24 =1,18. Затем по графику определяем Екр. Для этого находим точку пересечения линий K = 1,18 и d = 24 см и переносим ее на ось абсцисс – Екр = 215 мм. После этого определяем расстояние между симметричными пропилами в I и II проходах (см. рис. 31), пользуясь табл. 1 приложения.

Е1 = 153,9 мм; Е2 = 153,9 + 52,6 = 206,9 мм; Е3 = 206,9 + 40,4 = 246,9 мм;

Е1 = 61,8 мм; Е2 = 61,8 + 130,8 = 192,8 мм; Е3 = 192,8 + 52,6= 245,2 мм.

Отметим, что в I и во II проходах третьи доски будут укорочены, потому что Е3 > Екр. Затем по графику определяем ширину пласти бруса и ширину досок. Для этого на оси абсцисс находим соответствующее значение Е, проводим вертикальную линию до пересечения с окружностью соответствующего диаметра и на оси ординат определяем ширину досок.

Из графика видно, что ширина пласти бруса Вбр = 184 мм, ширина второй доски в I проходе, толщина которой 22 мм, составляет 125 мм. Во II проходе ширина досок, которые выпиливают из пласти бруса, будет равна толщине бруса – 150 мм. С учетам того, что Е3 > Вбр, они будут иметь небольшой обзол, который допускается в первом сорте обрезных досок. Допускается обзол шириной 5 мм длиной до 20% длины доски. В нашем примере ширина обзола будет
(192,8 – 184) / 2 = 4,4 мм, т. е. удовлетворяет требованиям стандарта.

Крайние доски в I и во II проходах будут укорочены. Определим их оптимальную ширину.

Для этого на оси абсцисс находим значение Е3, по вертикали поднимаемся к окружности, соответствующей комлевому диаметру D = 28,3 см. Точки пересечения переносим на вертикальную шкалу справа и определяем bопт. Для крайней доски I прохода находим Е3 = 246,9 мм и определяем bз(ст) = 75 мм и для крайней доски II прохода находим Е3 = 245,2 мм и определяем bз(ст) = 75 мм.

Для вычисления длины этих досок нужен расчетный диаметр. Для этого на оси ординат находим точку, соответствующую b = (75 + 2,3) = 77,3 мм, и проводим горизонтальную линию. На оси абсцисс находим точку, соответствующую Е3 = 246,9 мм, и проводим вертикальную линию. В точке пересечения этих горизонтальной и вертикальной линий dp = 25,9 см, для крайней доски II прохода dp = 25,7 см. Затем определяем длину этих досок.

Длина крайней доски I прохода будет l1(p) = (28,3 – 25,9) / 0,86 = 2,79 м – стандартная l1(ст) = 2,75 м.

Длина крайней доски II прохода l2(р) = (28,3 – 25,7) / 0,86 = 3,02 м – стандартная l2(ст) = 3 м.

Таким образом, в результате расчета постава получили следующие размеры досок (в метрах) и иx объем:

I проход м3

м3

II проход м3

м3

Объемный выход пиломатериалов из бревна составит ?Н = 100 · 0,179 / 0,27 = 66,3%.

Графический способ позволяет сравнительно быстро произвести расчет постава, однако в результате визуального определения размеров досок по графику точность расчетов несколько ниже, чем при аналитическом способе.

Источник