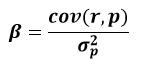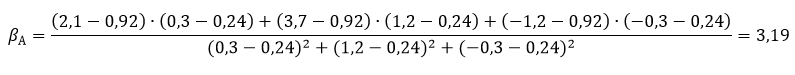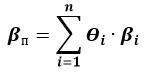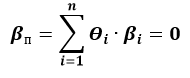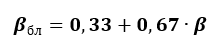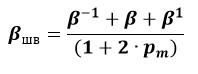Графический способ расчета коэффициента бета

Бета коэффициент

Риски: без их расчета на фондовом рынке никуда. В предыдущих статьях мы разбирали стандартное отклонение и дисперсию (в статье волатильность), как меру риска, сегодня поговорим о коэффициенте бета.

СОДЕРЖАНИЕ СТАТЬИ:

Коэффициент бета β – показатель ценной бумаги (портфеля), который рассчитывается как мера рыночного риска и дает оценку относительного изменения доходности ценной бумаги (портфеля) по сравнению с доходностью рынка в целом. Проще говоря, этот коэффициент показывает, как рынок воздействует на ценную бумагу.

Коэффициент бета необходим для:

— определения рыночного риска актива (портфеля) относительно рынка в целом;

— составление портфеля, нейтрального к риску;

— расчета оценки стоимости капитала.

Формула беты и ее возможные значения

Общепринятый подход к оценке параметра «бета акции» основывается на регрессионном анализе доходности акции относительно доходности фондового индекса.

Классическая бета или, как ее еще называют «сырая», необработанная бета (raw beta):

β – коэффициент бета;

cov (r, p) – ковариация ценной бумаги и портфеля (вместо портфеля часто применяют рыночный индекс, например, индекс Московской Биржи и индекс РТС);

r – доходность актива (ценной бумаги);

p – доходность портфеля (фондового индекса);

σ_p 2 – дисперсия портфеля (фондового индекса).

Значения, которые может принимать бета:

β = 1 – доходность такой бумаги будет изменяться одинаково с доходностью рынка (фондового индекса);

β > 1 – доходность (а также изменчивость) таких бумаг очень чувствительна к изменению рынка. Такие активы больше подвержены риску, но потенциально более доходны. В целом, такие ценные бумаги можно назвать агрессивными;

β – коэффициент бета;

r_i – доходность актива в i-ый момент времени;

p_i – доходность портфеля (индекса) в i-ый момент времени;

r _ср – доходность актива в i-ый момент времени;

р _ср – доходность портфеля (индекса) в i-ый момент времени;

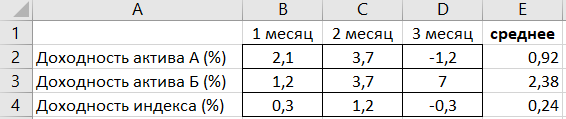
Пример для расчета беты

Совершим расчет беты для актива А

Тот же пример, но с расчетом в Excel

— с помощью опции вставить функцию :

А именно, =ИНДЕКС(ЛИНЕЙН(B2:D2;B4:D4);1) = 3,14

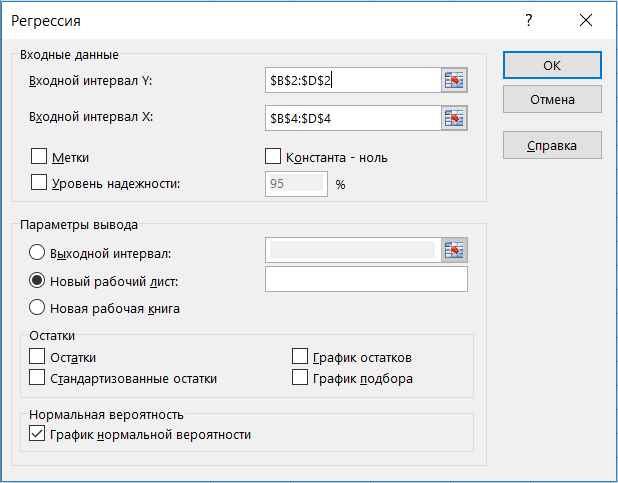
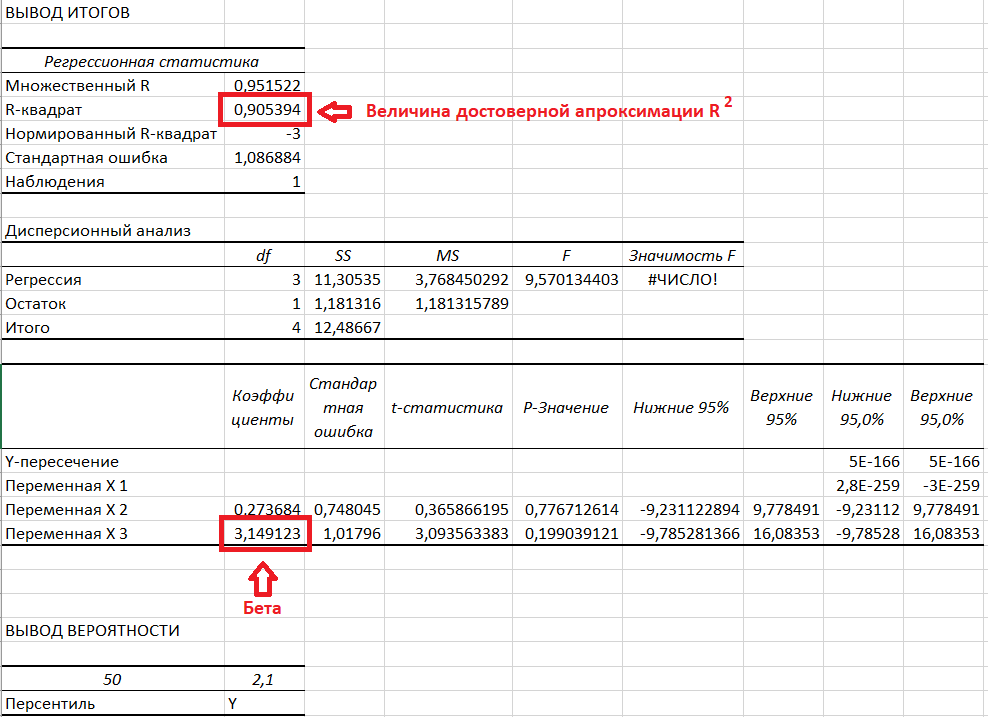
— с помощью пакета «анализ данных» в Excel (пример только для актива А):

Сначала нужно проверить наличие пакета «анализ данных», если не стоит, то установить в файл → параметры → надстройки. Затем в пакете выбираем опцию регрессия и делаем следующие манипуляции, согласно фото

Получаем следующие значения:

Как видим значения сошлись.

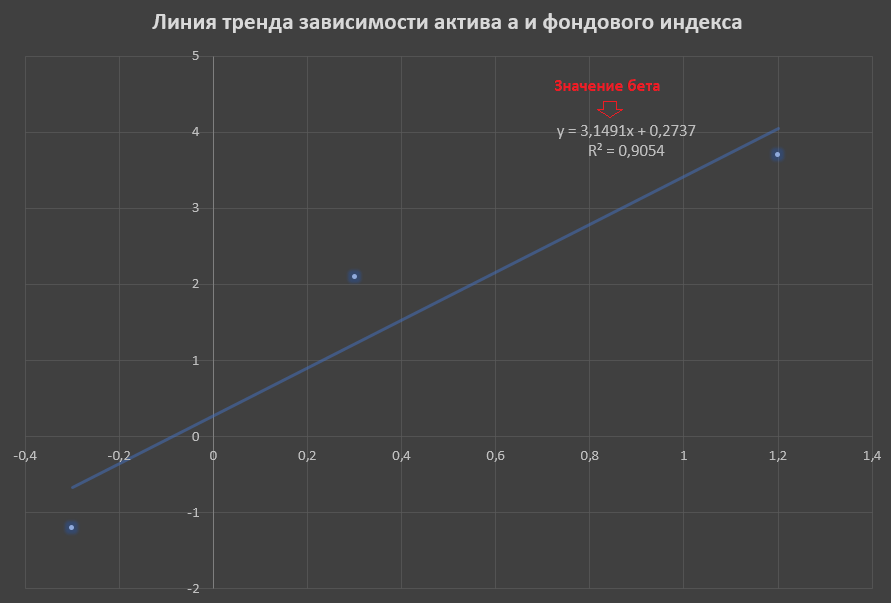
Теперь с помощью Excel покажем графическое представление бета:

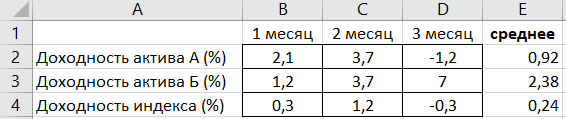
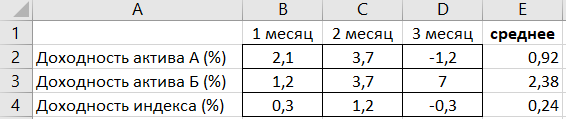
На основании данных, приведенных в таблице значений по месяцам построим точечный график зависимости доходности актива А от фондового индекса (в примере будем делать только для актива А)

По оси Х следует вводить значения доходности индекса, по Y — значения доходностей актива.

Уравнение тренда – это и есть уравнение линейной регрессии, в котором значение 3,1491 — значение бета. Таким образом можно сказать, что бета представляет собой наклон линии тренда. Значение беты показывает, что при повышении фондового индекса на 1, значение актива возрастает на 3,1491.

Бета портфеля, бета – нейтральный портфель.

Бета портфеля показывает совокупный риск вашего собственного портфеля относительно рынка. Важно понимать, как его рассчитать, чтобы составить портфель максимально нетерпимый к риску, а точнее, независимый от рынка.

Формула расчета беты портфеля:

β_п – коэффициент бета портфеля;

Θ_i – вес i-ого актива в портфеле;

β_i – бета i-ого актива в портфеле.

Рассчитаем бету портфеля, в активе которого есть актив А и Б

Возьмем данные из предыдущего примера, для расчетов примем вес актива А в портфеле 10%, актива Б — 90%.

Значение беты портфеля β_п = 3,14·0,1-1,8·0,9 = -1,306

Бета — нейтральный портфель и принципы его составления

Бета-нейтральный портфель, это частный случай, при котором бета портфеля равна нулю

Как же его получить?

Надо включить в портфель в дополнение к бумагам с положительной бетой, бумаги с отрицательной бетой и с такими весами, чтобы при подсчете беты портфеля она получилась равной нулю.

На практике достаточно мало портфелей имеют бету меньше нуля, но практически к ним можно отнести акции золотодобывающих компаний, т.к. в период кризисов они не просто не падают, а показывают существенный рост. (В России – это акций ПАО «Полюс» и ПАО «полиметалл»).

Включить в портфель активы, которые не куплены, а проданы (а точнее, в шорте). Т.к. актив в шорте, то перед бетой надо поставить знак -1.

Если нет желания считать бету самостоятельно, то посмотреть ее можно здесь:

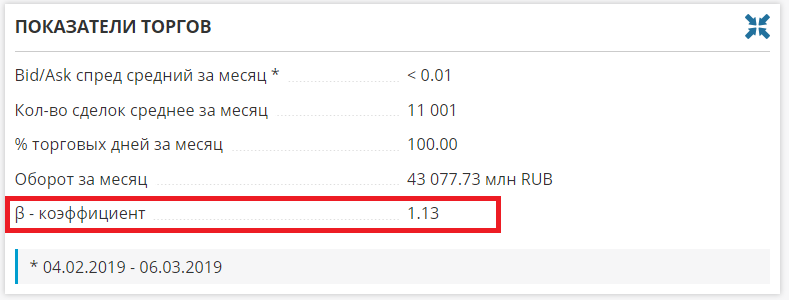
Бету всегда можно найти на сайте Московской Биржи, по ссылке:

На сайте investfunds.ru

Недостатки использования беты и их модификации

Как и у любой модели, у методики применения беты есть свои преимущества и недостатки. Многие эксперты пришли к выводу, что для любой акции ее бета не является устойчивым во времени показателем и поэтому не может служить точной оценкой будущего риска.

Для российского рынка характерны следующие недостатки применения модели классической беты:

1) Низкий показатель детерминации. Показывает долю риска, который присущ рыночному риску;

2) Мало информативные значения беты (которые нельзя применять) для акций малой ликвидности и капитализации;

3) Не применим к бумагам, у которых нету исторических цен (на длительном отрезке времени);

4) Коэффициент бета не может предусмотреть реальных положений дел в компаниях.

По всем этим причинам, описанным выше, были выведены модифицированные беты:

Наиболее популярные модификации представлены ниже (2 формулы)

Бета согласно Маршалу Блюму

Его расчеты показали, что со временем величина бета-портфеля приближается к единице, а внутренний риск компании стремится к среднеотраслевому или среднерыночному. Такую бету используют многие инвестиционные банки мира.

β_бл – бета по Маршалу Блюму;

β – коэффициент классической, сырой беты;

Бета согласно Шоулза-Виллимса

β_шв – бета по Маршалу Блюму;

— коэффициенты бета для предыдущего, текущего и последующего периода;

— коэффициент автокорреляции рыночной доходности.

Источник

CFA — Расчет бета-коэффициента и определение беты для инвестиционного проекта

Рассмотрим порядок оценки бета-коэффициента, используемого в модели CAMP, а также особенности расчета беты для непубличных компаний и отдельных инвестиционных проектов, — в рамках изучения корпоративных финансов по программе CFA.

При расчете средневзвешенной стоимости капитала (WACC) важно понять факторы риска, которые были рассмотрены при определении безрисковой ставки, премии за риск акций и бета-коэффициента, чтобы обеспечить согласованный расчет WACC и избежать двойного учета или упущения соответствующих факторов риска.

Когда финансовый аналитик использует модель CAPM для оценки стоимости собственного капитала (затрат на капитал), он должен оценить бета-коэффициент. Оценка бета-коэффициента обычно связана со множеством вариантов и сложностей.

Одним из распространенных методов расчета бета-коэффициента акций компании является использование регрессии рыночной модели доходности акций компании \( (R_i) \) в зависимости от рыночной доходности \( (R_m) \) за \( T \) периодов:

\( R_ = \hat a + \hat b R_ \) \(t = 1,2, \ldots T\)

Где \( \hat a \) представляет собой оценочный отрезок, отсекаемый линией регрессии, а \( \hat b \) является оценочным наклоном регрессии, которая используется для расчета бета-коэффициента.

Это уравнение обычно называют рыночной моделью (англ. ‘market model’), которая впервые была представлена ​​Майклом С. Дженсеном в публикации «The Performance of Mutual Funds in the Period 1945-1964«», Journal of Finance, Vol. 23, No. 2 (1969), стр. 389-416.

Однако оценка бета-коэффициента чувствительна к методу оценки и используемым данным. Вот некоторые из проблем, с которыми приходится сталкиваться:

Период оценки. Бета чувствительна к длительности периода оценки, и обычно оценивается с использованием данных за 2-9 лет. Выбор периода оценки — это компромисс между большим объемом данных за более длительные периоды оценки и конкретными изменениями в компании, которые лучше отражаются в более коротких периодах.

В целом, более длительные периоды оценки применяются к компаниям с долгой и стабильной историей операционной деятельности, а более короткие периоды оценки используются для компаний, которые претерпели значительные структурные изменения в недавнем прошлом (например, реструктурирование, недавнее приобретение или ликвидация подразделения) или изменения в финансовом и операционном рычаге.

Периодичность интервала доходности (например, дневной, недельный или месячный). Исследователи наблюдали меньшую стандартную ошибку в бета-коэффициенте, оцененном с использованием меньших интервалов доходности, таких как ежедневная доходность.

Выбор соответствующего рыночного индекса. Выбор рыночного индекса влияет на оценку бета.

Использование метода сглаживания. Некоторые аналитики корректируют историческую бета, чтобы отразить тенденцию стремления бета к 1. Например, выражение \( \beta_> = 0.333 + 0.667 \beta_i \) корректирует бета выше и ниже 1.0, сводя ее к 1.0.

Корректировки для акций с малой капитализацией. Акции с малой капитализацией обычно проявляют больший риск и большую доходность, чем акции с большой капитализацией в течение длительного периода. Исследователи Роджер Ибботсон, Пол Каплан и Джеймс Петерсон утверждают, что бета-коэффициенты для компаний с малой капитализаций должны корректироваться в сторону увеличения.

См.: Roger G. Ibbotson, Paul D. Kaplan, and James D. Peterson, “Estimates of Small Stock Betas Are Much Too Low,” Journal of Portfolio Management (1997), стр. 104-110.

Расчет бета-коэффициента для публичных компаний, как правило, не является проблемой из-за доступности данных о доходности акций, простоты расчета бета с использованием простой регрессии, а также наличия оценочных бета для публичных компаний от поставщиков данных для финансового анализа, таких как Barra, Bloomberg, DataStream Thompson Financials, Reuters и Line Value.

Как правило, проблема состоит в том, чтобы оценить бета-коэффициент для компании, чьи акции не торгуются публично, или оценить бета-коэффициент для проекта, который не является средним или типичным проектом публичной компании.

В этих случаях оценка бета требует использования информации о проекте или компании, в сочетании с бетой публичной компании.

Бета-коэффициент компании или проекта зависит от систематических компонентов бизнес-риска и от финансового риска. Оба этих фактора влияют на неопределенность денежных потоков компании или проекта.

Бизнес-риск или деловой риск (англ. ‘business risk’) компании или проекта — это риск, связанный с неопределенностью получения выручки, называемой риском продаж, а также связанный с операционным риском, который является риском, связанным со структурой операционных расходов компании.

Риск продаж или риск сбыта (англ. ‘sales risk’) зависит от эластичности спроса на продукцию, цикличности выручки и структуры конкуренции в отрасли.

Операционный риск (англ. ‘operating risk’) зависит от относительного сочетания постоянных и переменных операционных расходов: чем выше постоянные операционные расходы по отношению к переменным операционным расходам, тем больше неопределенность доходов и операционных денежных потоков.

Финансовый риск (англ. ‘financial risk’) — это неопределенность чистых доходов и чистых денежных потоков, связанных с использованием видов финансирования, которые имеют постоянную стоимость, таких ​​как долговое финансирование и аренда.

Чем больше используется постоянных источников капитала, относительно переменных источников, тем больше финансовый риск. Другими словами, компания, которая в значительной степени полагается на долговое финансирование вместо долевого финансирования, предположительно принимает больший финансовый риск.

Как финансовый аналитик оценивает бета-коэффициент для непубличной компании или проекта?

Один из обычных методов — это метод чистой игры (англ. ‘pure-play method’), который требует использования бета-коэффициента сопоставимой публичной компании, с корректировкой на различия в финансовом рычаге (леверидже), отражающие финансовый риск.

Сопоставимая компания (англ. ‘comparable company’) — это компания, имеющая аналогичный бизнес-риск. Причина, по которой этот подход называется методом чистой игры, заключается в том, что одним из самых простых способов идентификации сопоставимой компании для проекта является поиск в той же отрасли компании, которая ведет деятельность аналогичным образом.

Например, если аналитик изучает проект, связанный с аптечным бизнесом, соответствующими сопоставимыми компаниями в США могут быть Walgreens, CVS Corporation и Rite Aid Corporation.

Оценивая бету таким образом, аналитик должен сделать корректировки для учета разных уровней финансового рычага. Это требует процесса «де-левериджа» (устранение финансового риска) и «левериджа» (добавление финансового риска) бета-коэффициента (англ. ‘unlevering’, ‘levering’).

Бета-коэффициент сопоставимой компании сначала подвергается «де-левериджу», чтобы убрать из него финансовый риск.

Процесс де-левериджа и левериджа бета-коэффициента был разработан Робертом С. Хамада [“The Effect of the Firm’s Capital Structure on the Systematic Risk of Common Stocks,» Journal of Finance (Май 1972), стр. 435-452] и основан на теориях структуры капитала Франко Модильяни и Мертона Миллера.

Бета-коэффициент без финансового риска часто называют бетой активов или бетой для активов (англ. ‘asset beta’), потому что он отражает деловой риск активов.

После «де-левериджа» бета-коэффициента, мы корректируем его с учетом структуры капитала компании или проекта, что находится в центре нашего анализа. Другими словами, мы осуществляем «леверидж» беты активов, чтобы получить бета-коэффициент собственного капитала интересующего проекта или компании.

Для данной компании мы можем выполнить «де-леверидж» беты собственного капитала, чтобы оценить ее бету активов. Для этого мы должны определить взаимосвязь между бетой активов и бетой собственного капитала компании.

Поскольку риск компании делится между кредиторами и владельцами, мы можем представить риск компании \( \beta_<\text<активы>>\) как взвешенное среднее рыночного риска кредиторов компании \( \beta_<\text<долг>>\) и рыночного риска владельцев компании \( \beta_<\text<капитал>>\):

• \(E \) = рыночная стоимость собственного капитала,
• \(D \) = рыночная стоимость долга,
• \(w_d \) = доля долга = \( D / (D + E) \)
• \(w_e\) = доля собственного капитала = \( E / (D + E) \)

Но проценты по долгу вычитаются компанией при расчете налогооблагаемой прибыли, поэтому нагрузка долгового финансирования на самом деле ниже из-за вычета процентов.

Мы можем представлять бету активов компании как средневзвешенное значение беты долга и беты собственного капитала (акций), с учетом налогового эффекта от процентов:

где \( t\) — это предельная ставка налога.

Как правило, мы предполагаем, что долг компании не имеет рыночного риска, поэтому \( \beta_<\text<долг>> = 0 \). Это означает, что доходность по долгу не варьируется также, как рыночная доходность, что мы, как правило, считаем верным для большинства крупных компаний.

Если \( \beta_<\text<долг>> = 0 \), то упростив выражение \( \beta_<\text<капитал>> \) мы получим:

Следовательно, на рыночный риск собственного капитала компании влияет как рыночный риск активов \( \beta_<\text<активы>> \), так и фактор, представляющий систематическую часть финансового риска компании \( 1 + \left( (1-t) \right) \):

\( \mathbf < \beta_<\text<капитал>> = \beta_<\text<активы>> \left[ 1 + \left( (1-t) \right) \right] > \) (Формула 10)

Предположим, что компания имеет бету собственного капитала 1.5, коэффициент D/E (отношение долга к собственному капиталу) 0.4 и предельную ставку налога 30%. Используя Формулу 9, мы найдем, чтоб бета активов компании составляет 1.1719:

Другими словами, если бы у компании не было никакого долгового финансирования, то ее \( \beta_<\text<активы>> = \beta_<\text<капитал>> = 1.1719 \). Тем не менее, использование долгового финансирования увеличивает ее \( \beta_<\text<капитал>> \) с 1.1719 до 1.5.

Какой была бы бета собственного капитала компании, если бы коэффициент D/E был 0.5 вместо 0.4?

В этом случае мы применяем Формулу 10, используя коэффициент D/E 0.5:

Таким образом, расчет «де-левериджа» (устранение финансового риска по долговому финансированию) дает показатель рыночного риска для активов компании — игнорируя структуру капитала компании.

Мы используем расчет «левериджа» (добавление финансового риска по долговому финансированию) в Формуле 10 для оценки рыночного риска компании, учитывая конкретный риск активов, предельную налоговую ставку и структуру капитала.

Мы можем использовать те же расчеты «де-левериджа» и «левериджа» для оценки риска активов и риска собственного капитала для проекта.

Мы начинаем с беты собственного капитала сопоставимой компании, которая включает эффект финансового рычага \( \beta_> \), а затем преобразуем ее в эквивалентную бету активов сопоставимой компании без учета финансового риска долга \( \beta_> \).

Получив бету активов, мы можем использовать структуру капитала проекта и предельную налоговую ставку для преобразования этой беты активов в бету собственного капитала (акций) проекта \( \beta_> \).

Оценка бета коэффициента с использованием метода чистой игры.

Шаг 1: Выберите сопоставимую компанию. Определите сопоставимую компанию или компании с аналогичным бизнес-риском.

Шаг 2: Рассчитайте бету собственного капитала сопоставимой компании.

Шаг 3: Устраните финансовый риск из беты сопоставимой компании. Сделайте расчет «де-левериджа», устранив компонент финансового риска (для долгового финансирования) из беты собственного капитала, оставив в бете только компонент бизнес-риска.

Шаг 4: Добавьте в бету соответствующий финансовый риск проекта. Сделайте расчет «левериджа» для беты проекта, скорректировав бету активов на финансовый риск проекта.

Мы начинаем с оценки беты сопоставимой компании, включающей финансовый риск \( \beta_> \). Используя структуру капитала и налоговую ставку этой компании, мы оцениваем ее бету активов \( \beta_> \):

Затем мы учитываем финансовый рычаг рассматриваемого проекта или компании и рассчитываем риск собственного капитала \( \beta_> \).

Чтобы проиллюстрировать использование этих формул, предположим, что мы хотим оценить проект, который будет финансироваться долгом и собственным капиталом (акциями) в соотношении 0.4:1. Коэффициент D/E = 0.4 соответствует приблизительно 0.4/(0.4 + 1.0) = €0.286 на каждый евро необходимого капитала.

Мы находим сопоставимую компанию, работающую в том же направлении бизнеса, что и проект. Предельная налоговая ставка для компании, спонсирующей проект, и сопоставимой компания, составляет 35%.

Сопоставимая компания имеет бета-коэффициент 1.2 и коэффициент D/E 0.125.

Бета без финансового риска для сопоставимой компании составляет 1.1098:

Бета с учетом финансового риска для проекта составляет 1.3983:

\( \beta_> = 1.1098 \left[1 + (1 — 0.35) 0.4 \right] = 1.3983 \)

Затем мы используем 1.3983 в качестве бета-коэффициента в нашей оценке с помощью модели CAPM компонентов стоимости капитала (затрат на капитал) для проекта, и, в сочетании со стоимостью долга во взвешенном среднем (WACC), мы делаем оценку стоимости капитала для данного проекта.

В этом примере веса WACC составляют \(w_d \) = 0.4/1.4 = 0.2857, а \(w_e \) = 1/1.4 = 0.7143.

Пример (9) расчета беты активов.

Предположим, что бета собственного капитала публичной компании составляет 1.3, и что рыночная стоимость собственного капитала и долга составляет, соответственно, C$540 млн. и C$720 млн.

Если предельная налоговая ставка этой компании составляет 40%, то каким будет бета-коэффициент активов этой компании?

Решение:

Пример (10) расчета бета-коэффициента с использованием метода чистой игры.

AeroTechnique S.A. — частный бельгийский субподрядчик, поставляющий аэрокосмические детали. Хотя AeroTechnique не торгуется на бельгийской фондовой бирже, руководитель отдела развития оценить бета-коэффициент компании.

У него есть доступ к следующей информации:

• Средние бета-коэффициенты с учетом финансового риска и без учета финансового риска для группы сопоставимых компаний, работающих в разных странах Европы, составляют 1.6 и 1.0 соответственно.
• Коэффициент D/E AeroTechnique, основанный на рыночных данных, составляет 1.4.
• Ставка корпоративного налога AeroTechnique составляет 34%.

Решение:

Бета-коэффициент для AeroTechnique оценивается на основе средней беты группы сопоставимых компаний, из которой устранен финансовый риск. К этой бете применяется финансовая структура AeroTechnique:

\( \beta = 1.0 [1 + (1 — 0,34) (1.4)] = 1.924

Пример (11) оценки средневзвешенной стоимости капитала (WACC).

Bayern Chemicals KgaA является крупным немецким производителем промышленных, коммерческих и потребительских химических продуктов. Bayern Chemicals является частной компанией и ее акции не торгуются на бирже.

Финансовый директор компании поручил внешнему аналитику провести оценку компании и предоставил следующую информацию, чтобы рассчитать средневзвешенную стоимость капитала (WACC) компании:

• Номинальная безрисковая ставка соответствует ​​доходности долгосрочных 10-летних немецких гособлигаций. На дату оценки она составила 4.5%.
• Средняя долгосрочная историческая премия за риск акций в Германии составляет 5.7%.
• Ставка корпоративного налога для Bayern Chemicals составляет 38%.
• Коэффициент D/E составляет 0.7. Bayern поддерживает целевое значение коэффициента.
• Стоимость долга варьируется в пределах 225 базисных пунктов относительно 10-летних гособлигаций.

Иллюстрация 3 содержит дополнительную информацию о сопоставимых компаниях для Bayern Chemicals.

Источник