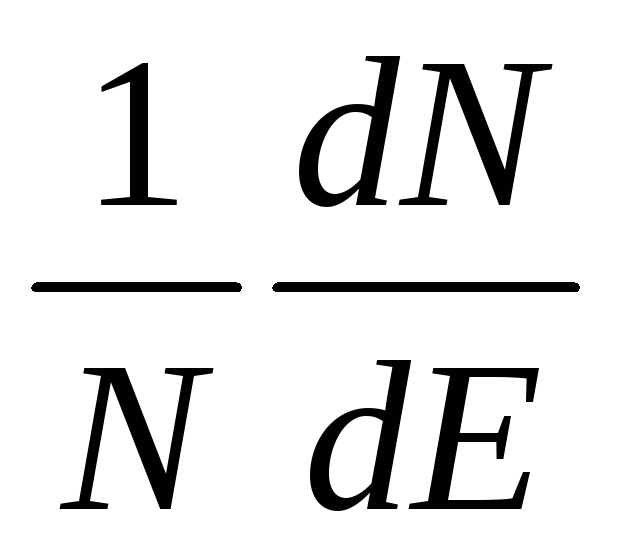Расчет энергии активации
Энергию активации можно рассчитать по экспериментальным данным графическим или аналитическим способами, используя уравнение Аррениуса
,
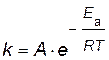
представив его в логарифмическом виде
 . | (4.14) |
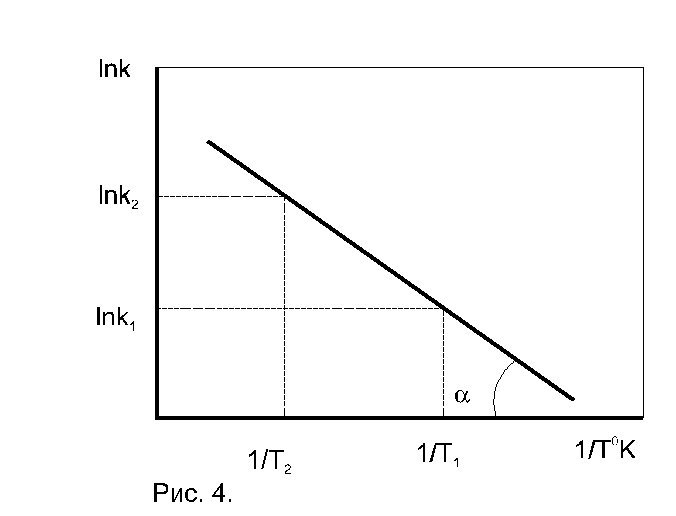
Графический способ. По экспериментальным значениям константы скорости реакции при различных температурах строят график зависимости lnk=f ( 
) (рис. 4.5).
Рис. 4.5. Зависимость константы скорости реакции от температуры
По тангенсу угла наклона прямой к оси абсцисс вычисляют энергию активации
.
Аналитический способ. Если предположить, что для выбранной реакции величины А и Еа постоянны в небольших пределах температур от Т1 до Т2, то:
;
.
В результате вычитания первого уравнения из второго получим
 . | (4.15) |
 . | (4.16) |
Под символом логарифма находится отношение констант скоростей реакции при двух температурах, поэтому константы можно заменить любыми пропорциональными им величинами при тех же температурах. Например, вместо констант скоростей можно подставить скорости реакции, если исходные концентрации реагирующих веществ при измерении скоростей в обоих опытах были одинаковы и скорость изменилась только под влиянием изменения температуры. Тогда получим следующие выражения:
Источник
Методы определения энергии активации:
По экспериментальным значениям константы скорости реакции: Графический метод (рис. 4):
(41)
(42)
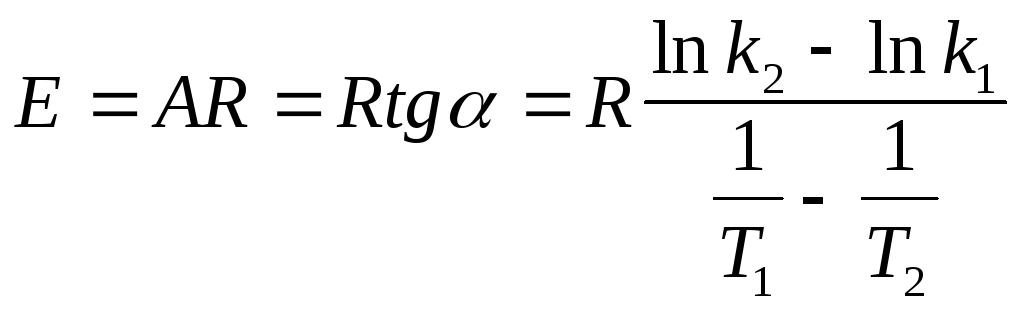
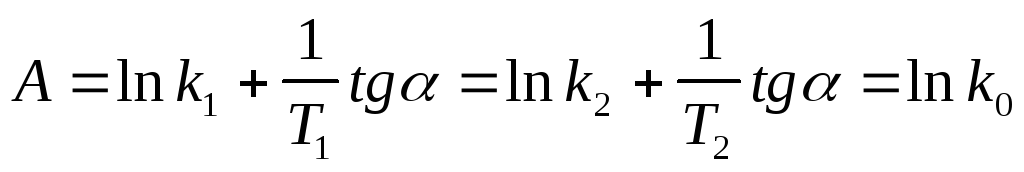
где k0 = k при Т =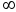 
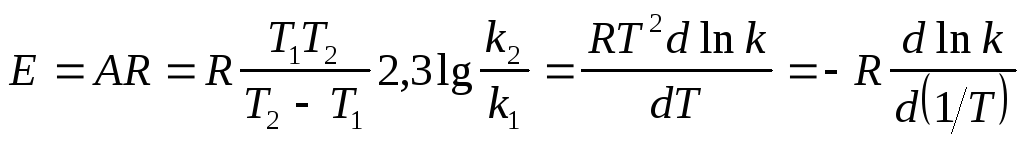
(экстраполяция).
(43)
Относительный температурный коэффициент константы скорости реакции:
(44)
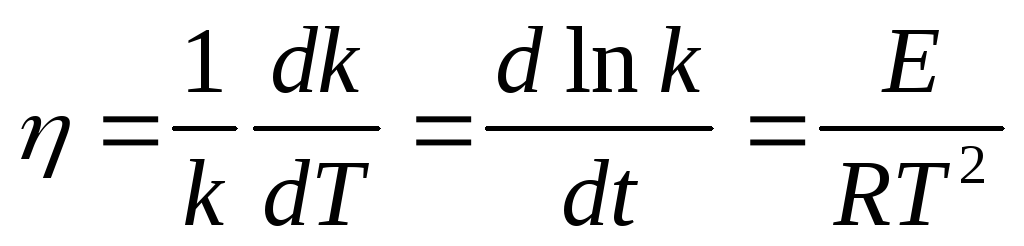
Коэффициент зависит от температуры и поэтому пригоден лишь для сравнительной оценки и ориентировочных расчетов в небольших интервалах температур.
Было сделано много попыток рассчитать теоретически энергию активации. Выдвинуты две основные теории: теория соударений и теория активированного комплекса.
Лекция 4 теория соударений
В 1918г. Льюис предположил, что для протекания реакции А + В = АВ должны столкнуться две молекулы А и В. Поэтому, зная число столкновений, можно, казалось бы, рассчитать скорость химической реакции. Однако если сравнить расчетное число соударяющихся молекул с числом реагирующих молекул, которое определяется экспериментально, то обнаруживаются два противоречия. Во-первых, число соударений примерно в 10 17 раз больше числа реагирующих молекул, т.е. из каждых 10 17 соударений только одно соударение является эффективным в осуществлении реакции. Во-вторых, в то время как при повышении температуры на 10 0 С число бинарных столкновений увеличивается примерно на 2%, скорость химической реакции возрастает на 200-300%.
Эти противоречия были разрешены при допущении, что реакция происходила только в том случае, если соударяющиеся молекулы обладали некоторой избыточной энергией; все остальные соударения неэффективны и не приводят к химической реакции, т.е. скорость реакции равна общему числу соударений, умноженному на долю эффективных соударений. Это допущение опиралось на изучение: 1) распределения скоростей реагирующих молекул и 2) влияния температуры.
Закон распределения скоростей. Все молекулы газа движутся с различными скоростями из-за частых соударений. Между молекулами постепенно происходит взаимообмен количеством движения и, следовательно, их скорости изменяются: одни молекулы увеличивают свою скорость, другие – уменьшают. Математический закон, которому подчиняется распределение скоростей и энергий, был найден Максвеллом и Больцманом в 1860г. Согласно этому закону, доля N/N молекул, обладающих большими скоростями, чем средняя скорость и , или кинетической энергией, превышающей величину ½ mи 2 , составляет:
( )
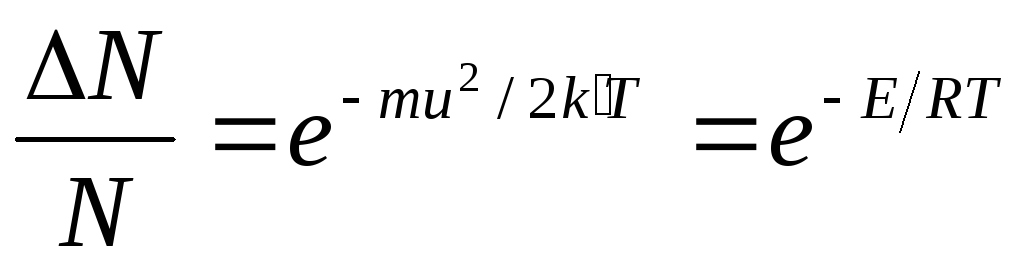
где k’ – константа Больцмана; u — средняя квадратичная скорость, см/с.
В дифференциальной форме это уравнение имеет вид:
, (45)
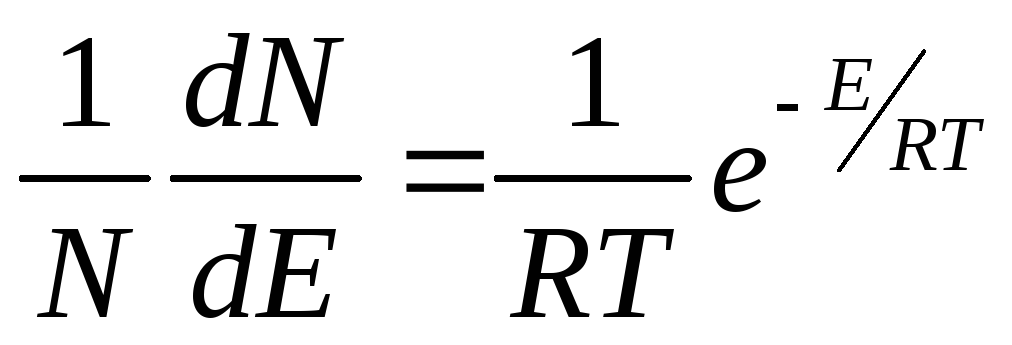
где R — универсальная газовая постоянная, эрг; Т — температура газа, К.
На рисунке 3 представлен график, построенный по уравнению (45). Доля молекул, энергия которых лежит в пределах определенного интервала, изображается площадью столбика, ограниченного кривой и соответствующими ординатами.
Рисунок 3. Распределение энергии по Максвеллу-Больцману.
В результате соударений всегда имеется несколько молекул с энергиями, намного превосходящими среднее значение. Таким образом, возможны столкновения между молекулами, имеющими высокую энергию активации, необходимую для реакции, но число таких соударений будет составлять очень небольшую долю от общего числа столкновений, происходящих в газе. Это объясняет тот факт, что лишь небольшая часть соударений приводит к реакции.
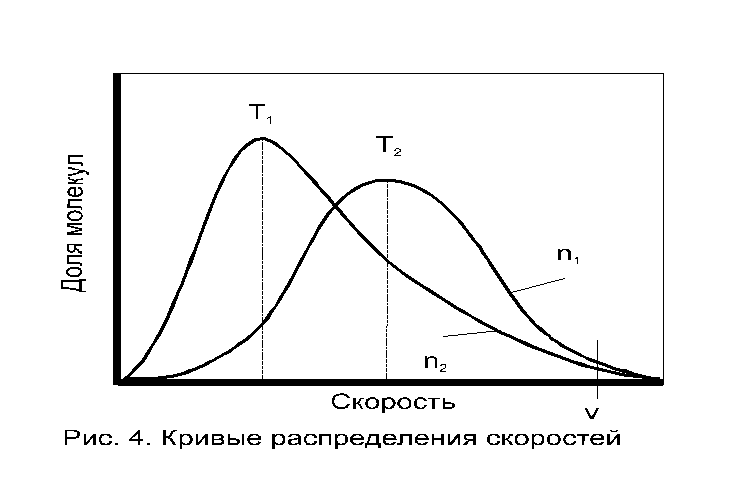
Влияние температуры на распределение скорости (см. Рис. 5.). С ростом температуры наблюдается смещение максимума в сторону более высокой скорости; происходит резкое увеличение числа молекул, имеющих скорости намного выше средней [при скорости имеется число (доля) молекул n1, при температуре Т1, которое увеличивается до n2 при температуре Т2, T2 > T1]. Общее число молекул, имеющих скорости, равные или большие определенного значения определяются площадью под кривой. Но именно небольшая доля молекул n1 и n2 при температурах Т1 и Т2 в конце кривых распределения, обладающих максимальными энергиями и скоростями в сечениях и будет определять эффективную долю столкновений, приводящих к их взаимодействию.
Экспоненциальный фактор в уравнении Максвелла учитывает изменение формы кривой при повышении температуры. Если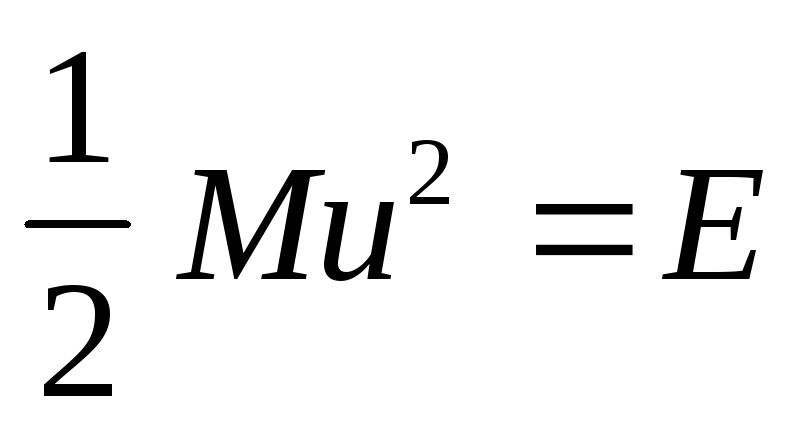 
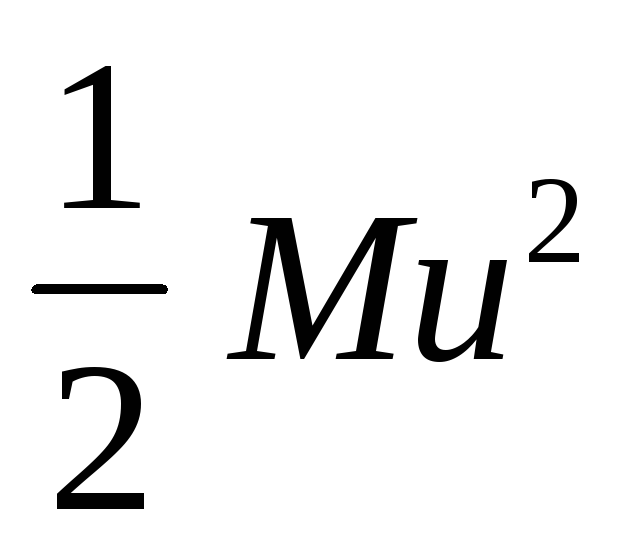
, где М – молекулярный вес, то член
будет представлять собой кинетическую энергию 1 моля молекул, каждая из которых имеет одну и ту же скоростьu . Член exp(-E/RT) называется фактором Больцмана. Этот фактор заметно увеличивается с увеличением температуры. Хотя общее число столкновений незначительно изменяется с ростом температуры, доля эффективных столкновений сильно повышается. Таким образом, отмеченное влияние температуры на скорость реакции может быть объяснено тем, что в газах (или растворах) имеются молекулы со всеми значениями скоростей и кинетических энергий. Число молекул с энергией, равной или большей, определенного значения Е, составляет приблизительно exp(-E/RT) часть от общего числа молекул. Так, например, повышение абсолютной температуры газа вдвое (например от 1000 К до 2000 К) приводит к увеличению средней кинетической энергии молекул в 2 раза, но доля молекул, обладающих энергией свыше 80 кДж/моль возрастает в 150 раз.
Источник
Методы расчета энергии активации химической реакции
Энергия активации – избыточная энергия, которой должны обладать частицы для вступления в химическую реакцию. Энергия активации является постоянной величиной для данной химической реакции и практически не зависит от температуры.
Чем больше активных молекул принимают участие в химической реакции, тем больше скорость реакции. Увеличение скорости реакции при повышении температуры обусловлено ростом доли активных молекул и числа столкновений между ними. Для определения величины энергии активации используют уравнение Аррениуса в интегральной и дифференциальной формах. Расчет энергии активации можно вести графическим и аналитическим способом.
Графический способ: Энергию активации графическим способом можно найти, если прологарифмировать уравнение Аррениуса:
 |
Аналитический способ:
Энергию активации химической реакции можно вычислить по значениям констант скоростей при двух различных температурах по уравнению:
 |
Отсюда, уравнение для расчета энергии активации имеет вид:
 |
Теоретический вывод уравнения Аррениуса сделан для элементарных реакций, но опыт показывает, что подавляющее большинство сложных реакций также подчиняются этому уравнению.
Дата добавления: 2015-01-30 ; просмотров: 125 | Нарушение авторских прав
Источник
Расчет энергии активации
Энергию активации можно рассчитать по экспериментальным данным графическим или аналитическим способами, используя уравнение Аррениуса
,
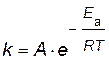
представив его в логарифмическом виде
 . | (4.14) |
Графический способ. По экспериментальным значениям константы скорости реакции при различных температурах строят график зависимости lnk=f ( 
) (рис. 4.5).
Рис. 4.5. Зависимость константы скорости реакции от температуры
По тангенсу угла наклона прямой к оси абсцисс вычисляют энергию активации
.
Аналитический способ. Если предположить, что для выбранной реакции величины А и Еа постоянны в небольших пределах температур от Т1 до Т2, то:
;
.
В результате вычитания первого уравнения из второго получим
 . | (4.15) |
 . | (4.16) |
Под символом логарифма находится отношение констант скоростей реакции при двух температурах, поэтому константы можно заменить любыми пропорциональными им величинами при тех же температурах. Например, вместо констант скоростей можно подставить скорости реакции, если исходные концентрации реагирующих веществ при измерении скоростей в обоих опытах были одинаковы и скорость изменилась только под влиянием изменения температуры. Тогда получим следующие выражения:
Источник
