Графический способ представления случайной величины

Графическое представление случайной величины

Для определения вида закона распределения случайной величины удобно представить данные наблюдений в графическом виде. Для графического представления данных наблюдения используется специальный график – гистограмма (рисунок 3.1).

Рисунок 3.1 – Гистограмма и полигон распределения

Гистограмма является важным вспомогательным средством при принятии гипотезы о виде функции распределения. Поэтому необходимо извлечь из нее максимум информации. Дело в том, что форма гистограммы зависит от числа и величины интервалов разбиения. При слишком малом числе интервалов разбиения (интервал велик), плохо выявляются характерные особенности распределения. С ростом числа интервалов характерные особенности выявляются все лучше, но лишь до определенного предела. При большом числе интервалов (интервал слишком мал) гистограмма снова теряет характерные особенности распределения, превращаясь в пределе (когда в каждом интервале не более одного значения) в чередование «пустых» интервалов и одинаковых по высоте прямоугольников.

Наиболее простой способ разбиения вариационного ряда — это использование равновеликих интервалов, количество которых определяется по специальным формулам, например, по формуле (2.6).

Согласно этому правилу при объеме выборки до тысячи полных реализаций рекомендуемое число интервалов разбиения не превышает одиннадцати. Для объемов выборки n

По данным статистического ряда можно вычислить еще одну характеристику случайной величины — эмпирическую интегральную функцию распределения. Значение эмпирической интегральной функции распределения для j-ого интервала Fj определяется по формуле:

(3.2)

Функция распределения F(x) может быть представлена в виде графика, который строится подобно гистограмме, только высоты прямоугольников равны значениям функции распределения соответствующих интервалов.

Пример графика приведен на рисунке 3.2.

Рисунок 3.2 – График эмпирической интегральной функции

распределения опытных данных

Интегральная функция распределения является более универсальной характеристикой распределения по сравнению с гистограммой, которая определяет вероятность того события, что случайная величина X будет меньше или равна заданному значению x. Эмпирическая интегральная функция распределения определяет частость (опытную вероятность) события X ≤ x.

Пример 5 Построим гистограмму и график интегральной функции распределения для данных из примера 2.

В качестве первого приближения принимаем число интервалов, рассчитанное по формуле Стенжерса.

Принимаем число интервалов k = 6, ширина интервала Δx = 43,3.

В этом случае имеем одну инверсию (при переходе с 5 на 6 интервал).

Принимаем число интервалов k = 7, ширина интервала Δx = 37,13.

Расчеты сведены в таблицу 3.1.

Таблица 3.1 – Подсчет частот

Номер интервала	Границы интервалов	Середина интервала, xj	Число попаданий, mj
1	70 -107,1	88,6	1
2	107,1 -144,3	125,7	1
3	144,3-181,4	162,8	4
4	181,4 -218,5	200,0	9
5	218,5-255,6	237,1	11
6	255,6-292,8	274,2	15
7	292,8-329,9	311,3	4

В этом случае опять получаем одну инверсию.

Принимаем число интервалов k = 8, ширина интервала Δx = 32,5

Расчеты сведены в таблицу 3.2

Таблица 3.2 – Подсчет частот

Номер интервала	Границы интервалов	Середина интервала, xj	Число попаданий, mj
1	70 -102,5	86,24	1
2	102,5-135	118,7	1
3	135-167,5	151,2	3
4	167,5 -200	183,7	7
5	200-232,4	216,2	9
6	232,4-264,9	248,7	10
7	264,9-297,4	281,2	11
8	297,4-329,9	313,7	3

И в этом случае получаем одну инверсию.

Принимаем число интервалов k = 9, ширина интервала Δx = 28,9.

Расчеты сведены в таблицу 3.3.

Таблица 3.3 – Подсчет частот

Номер интервала	Границы интервалов	Середина интервала, xj	Число попаданий, mj
1	70 -98,88	84,4	1
2	98,88-127,8	142,2	0
3	127,8-156,6	200,0	3
4	156,6-185,5	257,7	4
5	185,5-214,4	315,5	7
6	214,4-243,3	373,2	9
7	243,3-272,1	431,0	12
8	272,1-301	488,7	7
9	301-329,9	315,5	2

В данном случае имеем две инверсии (при переходе с 1 на 2 интервал и с 7 на 8). Таким образом принимаем количество интервалов, равное 8, т.к. количество инверсий минимально, а количество интервалов наибольшее.

Источник

Графическое представление распределения случайной величины. Описательная статистика включает графическое отображение выборки случайных величин.

Описательная статистика включает графическое отображение выборки случайных величин.

1. Гистограмма – столбчатая диаграмма, показанная на рис. 9, является наиболее широко используемой графической формой представления распределения случайной величины. Ее размах делится на интервалы, и их значения откладываются на горизонтальной оси. Каждому интервалу отвечает вертикальный столбик с высотой, равной частоте случайной величины.

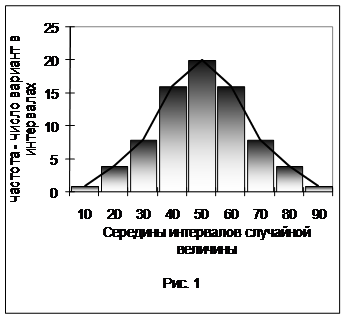
2. Полигон частот – это график в виде ломанной лини, соединяющей середины верхних оснований интервальных столбиков, как показано на рис. 9.

В аналогии распределения случайных величин с рассеянием песка, гистограмме отвечает вертикальный разрез через вершину кучи песка со ступенчатой (соответственно интервалам) поверхностью. Полигон частот на таком вертикальном разрезе можно имитировать сглаживанием песчаных ступенек.

Необходимым, но, к сожалению, недостаточным условием однородности распределения является одновершинность гистограммы и полигона частот – их мономодальность.

3.Накопительная (иначе: интегральная, кумулятивная) гладкая кривая или ломаная линия, т.е. полигон накопленных частот, и соответствующая столбиковая диаграмма, показанные на рис. 10, являются графическими формами отображения эмпирической функции распределения F(x).

При этом по горизонтальной оси откладываются значения случайной величины.

По вертикальной оси для интервалов откладываются накопленные частоты, получающиеся добавлением к частоте интервала суммы частот интервалов, расположенных левее. Для первого, самого левого интервала, ордината равна его частоте. Для второго интервала ордината складывается из его частоты и частоты первого интервала. Ордината третьего интервала получается прибавлением его частоты к сумме частот первого и второго интервалов и т.д.

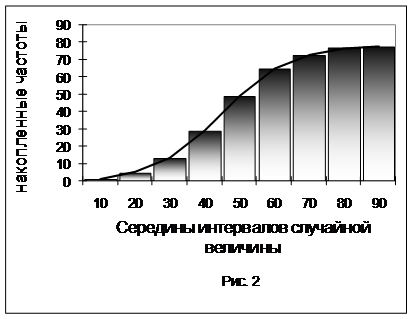
Такие накопленные частоты, выраженные в долях объема (от 0 до 1), рассматриваются, как эмпирические функции распределения F(x). Однородные выборки характеризуются гладкими эмпирическими накопительными кривыми, которые удобно сравнивать с теоретическими распределениями.

Источник

Графическое представление распределения случайной величины. Графические изображения статистических данных облегчают их обобщение и анализ

Графические изображения статистических данных облегчают их обобщение и анализ. Графики применяются для характеристи­ки развития явления во времени, в пространстве, отображения структуры явления и структурных сдвигов, при контроле за вы­полнением плана, изучении взаимосвязи между явлениями.

По способу построения графики делятся на диаграммы, кар­тограммы и картодиаграммы.

Диаграмма— изображение статистических данных при помо­щи геометрических фигур, линий, точек.

Картограмма— это географическая (контурная) карта, которая графически характеризует пространственное распределение ка­кого-либо статистического показателя путем различной окраски, штриховки и т. д. (например, плотность населения в различных регионах).

Картодиаграмма— это совмещение картограммы с диаграм­мой, т. е. в отдельных районах условными знаками наносят абсо­лютные значения статистических показателей.

Самым распространенным видом графиков являются диа­граммы, которые делятся на линейные, столбиковые, структур­ные, фигурные, знаки Варзара и др.

Линейные диаграммы— наиболее простой способ наглядного изображения статистических данных, когда изучаемое явление представляется в виде отрезков ломаной линии, называемой ста­тистической кривой. Они применяются для характеристики и сравнения развития различных явлений во времени, пространст­ве, а также для отображения взаимосвязи между явлениями.Для построения линейной диаграммы используется прямо­угольная система координат. На оси абсцисс (по горизонтальной шкале) откладываются равные отрезки, представляющие собой периоды времени, на ось ординат наносят масштаб для отображе­ния уровня явления. Соединение точек, построенных на коорди­натной системе, дает ломаную линию, представляющую собой закономерность развития явления.Рекомендуется строить координатную сетку с учетом соотно­шения масштабов по осям координат примерно 1:1,5 (правило «золотого сечения»), т. е. с учетом соотношения масштабов по сторонам занятого графиком пространства по вертикали и гори­зонтали. Преимуществом линейных графиков является то, что на од­ном графике имеется возможность отображения закономерности нескольких явлений. Разновидностью линейных диаграмм явля­ются контрольно-плановые графики, обеспечивающие оператив­ный контроль за ходом выполнения задания как за отдельные промежутки (дни, пятидневки), так и нарастающим итогом с на­чала периода. Для сравнения различных величин между собой и для изобра­жения динамики могут быть использованы столбиковые (ленточ­ные) диаграммы.Для их построения также используется система прямоугольных координат. Основания столбиков одинакового размера, представляющие собой периоды времени (годы, меся­цы, дни), размещаются на оси абсцисс, а вершины столбиков со­ответствуют величине изучаемого показателя. Столбиковые диа­граммы называют ленточными, если столбики расположены го­ризонтально в виде лент.

Структурные диаграммыприменяются для изображения струк­туры явления и характеристики структурных сдвигов. При пост­роении таких графиков состав совокупности выражается относи­тельными величинами структуры, исчисленными в процентах. Они могут быть двух видов: столбиковые и круговые. Общая вы­сота столбика и площадь круга отображают целое и принимаются соответственно за 100%. При построении круговой диаграммы необходимо проценты перевести в градусы, учитывая, что каждый процент равен 3,6° (360: 100).

Знаки Варзара(по имени статистика В. Е. Варзара) являются разновидностью столбиковых диаграмм. Они позволяют отобра­зить на графике сложное явление, представляющее собой произ­ведение двух показателей. Например, объем продукции — произ­ведение производительности труда и численности работников. Если в прямоугольнике одну сторону взять пропорционально уровню производительности труда, а другую — пропорционально численности работников, то площадь прямоугольника будет пропорциональна объему произведенной продукции.

Одномерная выборка случайной величины графически представляется гистограммой, полигоном частот и их накопительными аналогами.

Гистограмма – столбчатая диаграмма (рис. 1.1, диаграмма 1), широко используемая для иллюстрации распределения случайной величины.

По горизонтальной оси откладываются интервалы случайной величины, получаемые делением размаха на обычно равные части. Каждый интервал является основанием вертикального столбца, высота которого отражает частоту попадания в него вариант. Высота столбца может быть выражена как частость, то есть доля попавших в интервал вариант по отношению ко всему объему выборки. Соответственно сумма высот всех столбцов равна объему выборки или единице.

Количество интервалов, на которые делится размах, не должно быть слишком большим, так как при этом в интервалы попадет мало вариант и частоты будут слишком неустойчивыми. Это следует из примера с подбрасыванием монеты. При небольшом числе подкидываний количество выпадений «орла» может составлять от 0 до 100%, но по мере увеличения подкидываний количество выпадений «орла» будет приближаться к 50%, то есть истинной вероятности явления. Естествоиспытатель XVIII века Ж. Бюффон при 4040 подкидываниях монеты получил частость выпадений орла 0,5080. У известного статистика К. Пирсона при 12000 подкидываниях частость составила 0,5016 и при 24000 – 0,5005. Опыты подтверждают за кон больших чисел – теорему Бернулли об асимптотической сходимости частот событий к их вероятностям при увеличении числа испытаний.

При малом количестве интервалов, на которые делится размах, в интервалы попадает больше вариант и частота оценивается более надежно, но теряется детальность отображения распределения случайной величины.

Ясно, что количество интервалов прямо зависит от объема выборки и примерно подсчитывается как 1 + 3,32lgN, где N – объем выборки. Например, для объема 100 вариант получается ≈8 интервалов, при увеличении выборки до 500 вариант количество интервалов возрастает до 10. Подсчеты носят ориентировочный характер, и количество интервалов корректируется соответственно особенностям эмпирического распределения.

Полигон частот – это график в виде ломаной линии (рис. 1.1, график 2), которая соединяет середины верхних оснований интервальных столбцов.

Гистограмма при имитации рассеяния случайной величины кучей песка со ступенчатой поверхностью отвечает вертикальному сечению через вершину. Полигон частот в таком вертикальном сечении получается при сглаживании ступеней.

Необходимым, но, к сожалению, недостаточным условием однородности распределения является одновершинность гистограммы и полигона частот, то есть их мономодальность.

Накопительная (иначе – интегральная, кумулятивная) гладкая кривая или ломаная линия, то есть полигон накопленных частот (рис. 1.2, график 2) и соответствующая

столбиковая диаграмма (рис. 1.2, диаграмма 1), являются графическими формами отображения эмпирической функции распределения F(x).

При этом по горизонтальной оси откладываются значения случайной величины. По вертикальной оси для интервалов откладываются накопленные частоты, получающиеся добавлением к частоте текущего интервала суммы частот интервалов, расположенных левее. Для первого, самого левого, интервала ордината равна его частоте. Для второго интервала ордината складывается из его частоты и частоты первого интервала. Ордината третьего интервала получается прибавлением его частоты к сумме частот первого и второго интервалов и т.д.

Такие накопленные частоты, выраженные в долях объема (от 0 до 1), рассматриваются как эмпирические функции распределения F(x). Однородные выборки характеризуются гладкими эмпирическими накопительными кривыми, которые удобно сравнивать с теоретическими распределениями.

Источник