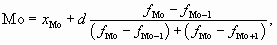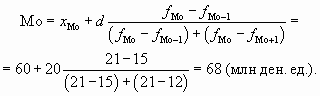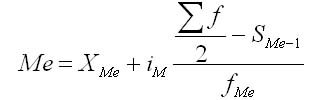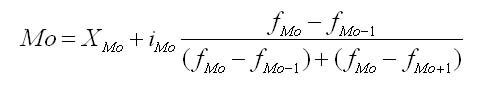Графический способ определения моды

Структурные характеристики вариационного ряда распределения

8.1. Мода

Мода (Мо) — это наиболее часто встречающееся значение признака, или иначе говоря, значение варианты с наибольшей частотой. В дискретных и интервальных рядах моду рассчитывают по-разному.

8.1.1. Определение моды в дискретных вариационных рядах

В дискретных вариационных рядах для определения моды не требуется специальных вычислений: значение признака, которому соответствует наибольшая частота, и будет значением моды.

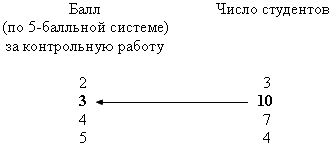
Пример 8.1. По представленным ниже результатам проведения контрольной работы по статистике определим моду.

Здесь наибольшая частота — 10, она принадлежит варианте со значением 3, значит, Мо = 3. Таким образом, самой распространенной оценкой, полученной студентами за контрольную работу, была «тройка».

8.1.2. Определение моды в интервальных вариационных рядах с равными интервалами

Для определения моды в интервальных вариационных рядах с равными интервалами сначала находят модальный интервал, которым является интервал с наибольшей частотой, а затем ведут расчет по формуле

где х_Мо — нижняя граница модального интервала;

d — величина интервала;

f_Mo — частота модального интервала;

f_Mo — 1 — частота интервала, предшествующего модальному;

f_Mo + 1 — частота интервала, следующего за модальным.

Пример 8.2. Имеются данные по группе банков.

Таблица 8.1.

Сумма выданных кредитов, млн ден. ед.	Количество банков
До 40	8
40-60	15
60-80	21
80-100	12
100-120	9
120-140	7
140 и выше	4
Итого	77

Определим модальный размер выданных кредитов:

1. модальным является интервал 60-80, так как ему соответствует наибольшая частота (21);
2. нижняя граница модального интервала x_Мо = 60; величина интервала d = 20 (80 — 60 = 20);
3. частота модального интервала f_Мо = 21; частота интервала, предшествующего модальному, f_Мо — 1 = 15; частота интервала, следующего за модальным, f_Мо + 1 = 12.

Подставив в формулу соответствующие величины, получим

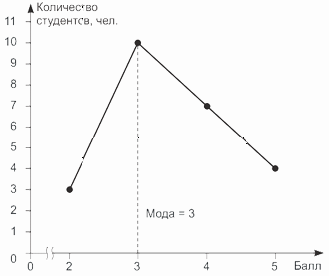
Определить модальное значение признака можно и по графику. Для этого в случае дискретных вариационных рядов строится полигон распределения. Напомним, что у него на оси абсцисс помещаются значения признака (варианты), а на оси ординат — соответствующие им частоты. Значение абсциссы, соответствующее наибольшей вершине полигона, будет значением моды.

Пример 8.3. По результатам проведения контрольной работы по статистике, приведенным в примере 8.1, определим моду графическим способом.

Для этого построим полигон распределения и найдем абсциссу его вершины (рис. 8.1).

Если имеется интервальный вариационный ряд с равными интервалами, то для определения моды строится гистограмма, у которой на оси абсцисс находятся значения границ интервалов, а на оси ординат — соответствующие интервалам частоты. На гистограмме модальный интервал будет иметь наибольшую высоту столбца. Затем надо провести линии, соединяющие вершины модального столбца с прилегающими вершинами соседних столбцов. Для нахождения значения моды из точки пересечения проведенных линий на ось абсцисс опускают перпендикуляр. Абсцисса точки пересечения будет значением моды. Продемонстрируем это на примере.

Пример 8.4. По данным о распределении банков по сумме выданных кредитов, приведенным в примере 8.2, определим моду графическим способом (рис. 8.2).

Вариационный ряд может содержать несколько модальных значений. Чаще всего это происходит, когда в один ряд объединяют разнородные единицы наблюдения, которые желательно разделить на подгруппы и анализировать по отдельности. Вариационный ряд, имеющий одну моду, называется унимодальным, две — бимодальным, три и более — мультимодальным.

Источник

Мода и медиана

Медиана в статистке

Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда.

Посмотреть решение задачи на нахождение моды и медианы Вы можете здесь

В ранжированных рядах несгруппированные данные для нахождения медианы сводятся к поиску порядкового номера медианы. Медиана может быть вычислена по следующей формуле:

где Хm — нижняя граница медианного интервала;
im — медианный интервал;
Sme— сумма наблюдений, которая была накоплена до начала медианного интервала;
fme — число наблюдений в медианном интервале.

Свойства медианы

1. Медиана не зависит от тех значений признака, которые расположены по обе стороны от нее.
2. Аналитические операции с медианой весьма ограничены, поэтому при объединении двух распределений с известными медианами невозможно заранее предсказать величину медианы нового распределения.
3. Медиана обладает свойством минимальности. Его суть заключается в том, что сумма абсолютных отклонений значений х, от медианы представляет собой минимальную величину по сравнению с отклонением X от любой другой величины

Графическое определение медианы

Для определения медианы графическим методом используют накопленные частоты, по которым строится кумулятивная кривая. Вершины ординат, соответствующих накопленным частотам, соединяют отрезками прямой. Разделив поп олам последнюю ординату, которая соответствует общей сумме частот и проведя к ней перпендикуляр пересечения с кумулятивной кривой, находят ординату искомого значения медианы.

Определение моды в статистике

Мода — значение признака, имеющее наибольшую частоту в статистическом ряду распределения.

Определение моды производится разными способами, и это зависит от того, представлен ли варьирующий признак в виде дискретного или интервального ряда.

Нахождение моды и медианы в контрольных по статистике происходит путем обычного просматривания столбца частот. В этом столбце находят наибольшее число, характеризующее наибольшую частоту. Ей соответствует определенное значение признака, которое и является модой. В интервальном вариационном ряду модой приблизительно считают центральный вариант интервала с наибольшей частотой. В таком ряду распределения мода вычисляется по формуле:

где ХМо — нижняя граница модального интервала;
imo — модальный интервал;
fм0, fм0-1,, fм0+1 — частоты в модальном, предыдущем и следующем за модальным интервалах.

Модальный интервал определяется по наибольшей частоте.

Мода широко используется в статистической практике при анализе покупательного спроса, регистрации цен и т. д.

Соотношения между средней арифметической, медианой и модой

Для одномодального симметричного ряда распределения средняя арифметическая, медиана и мода совпадают. Для асимметричных распределений они не совпадают.

К. Пирсон на основе выравнивания различных типов кривых определил, что для умеренно асимметричных распределений справедливы такие приближенные соотношения между средней арифметической, медианой и модой:

Источник