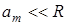Графический способ определения длины волны
Цель работы: Ознакомиться с методами получения когерентных источников, изучить явление интерференции света в тонких пленках (полосы равного наклона и равной толщины).
Приборы и принадлежности: бипризма Френеля, поляризационный микроскоп МП-7, окулярные микрометры, светофильтры, оптическая скамья, плоско-выпуклая линза, источники света (теневые проекторы).
Краткая теория . Интерференцией света называется явление наложения двух или нескольких когерентных волн, распространяющихся вдоль одного направления, в результате которого происходит перераспределение энергии в пространстве, т.е. чередование максимумов и минимумов интенсивности. Волны называются когерентными, если разность фаз 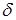
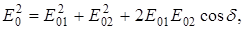
где 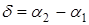
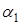
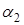
В случае некогерентных волн 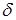
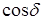
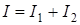
В случае когерентных волн 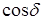
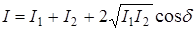
Особенно интерференция отчетливо проявляется в случае, когда 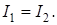
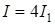
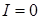
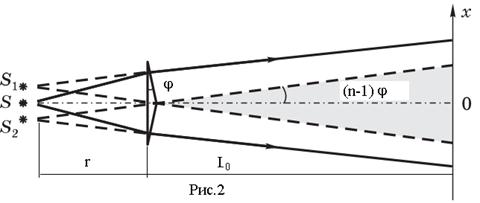
Когерентные световые волны можно получить, разделив волну, излучаемую одним источником, на две части. Если заставить эти две волны пройти разные оптические пути, а потом наложить их друг на друга, наблюдается интерференция. Пусть разделение на две когерентные волны происходит в точке
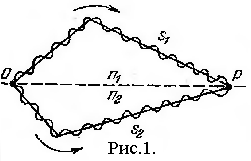
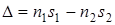

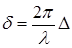
Из этой формулы видно, что если оптическая разность хода равна целому числу длин волн
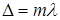
то разность фаз 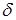
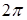
Если 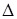
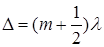
то 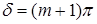
Разным точкам экрана соответствуют разные значения разности хода слагаемых волн. Поэтому на экране регулярно чередуются полосы максимальной и минимальной интенсивности, если источником является узкая щель, параллельная экрану. Такая устойчивая во времени картина называется интерференционной картиной.
Для количественной характеристики интерференционной картины вводят параметр 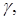
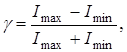
где 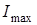
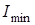
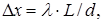
где 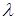


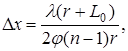
где 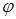
Измерения: Бипризма помещается на расстоянии 10- 15 см от щели так, чтобы ребро тупого угла бипризмы было расположено вертикально. На расстоянии 55- 75 см от бипризмы помещают окулярный микрометр. Цена деления окулярного микрометра равна 0,01 мм . Осветитель, щель, бипризма и окулярный микрометр должны быть строго установлены на одной высоте оптической скамьи.
Сделав щель достаточно узкой, слегка поворачивают бипризму около горизонтальной оси, добиваясь такого положения, чтобы ребро бипризмы было строго параллельно щели. При такой установке интерференционная картина будет наиболее отчетливой. Перед осветителем ставят красный светофильтр. Окулярный микрометр устанавливают на расстоянии 65 см от щели. С его помощью определяют не менее пяти расстояний 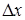
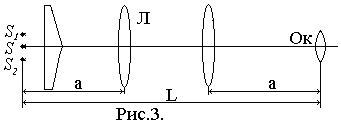
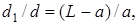
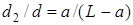
откуда 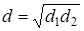

Подставляя (10) в (7), вычисляют длину волны по формуле:
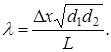
Таким образом, при данном L для пяти значений 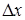
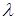
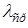
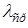
2. Определение радиуса кривизны линзы и длины световой волны с помощью колец Ньютона.
Задача посвящена явлению интерференции света в тонких прозрачных изотропных пленках, в частности, когда интерференционная картина локализована на поверхности тонкого клина (полосы равной толщины, метод деления амплитуды). Наблюдение интерференции с помощью колец Ньютона представляет собой наиболее простой метод изучения этого явления и определения длины световой волны.
Интерференционную картину полос равной толщины можно наблюдать от воздушной прослойки, образованной плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой или двояковыпуклой линзой. В этом случае геометрическим местом точек равной толщины является окружность и, поэтому соответствующие полосы равной толщины будут иметь вид концентрических окружностей с центром в точке соприкосновения линзы с плоскопараллельной пластинкой. В отраженном свете в центре интерференционной картины будет наблюдаться минимум. Схема, с помощью которой наблюдаются кольца Ньютона, представлена на рис.4. Так как интерференция происходит между волнами, отраженными от нижней и верхней поверхностей воздушной 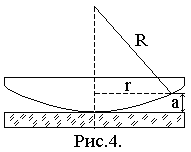
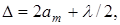
где am — толщина воздушной прослойки (показатель преломления воздуха n=1). am легко вычисляется из геометрических соображений при условии
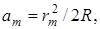
где rm — радиус m — го кольца, R — радиус кривизны линзы.
Условие образования m — го темного кольца имеет вид
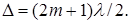
Из формул (12), (13), (14) получим

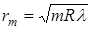
Чем больше m, тем меньше различие между радиусами соседних колец.
Для радиусов светлых колец в отраженном свете будем иметь
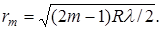
Вследствие упругой деформации невозможно соприкосновение сферической линзы и плоской пластинки строго в одной точке. Поэтому более правильный результат получится, если R и 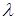
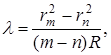
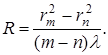
На опыте трудно измерять rm и rn . Разность квадратов радиусов можно заменить разностью квадратов хорд m— го и n— го колец 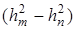
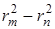
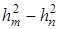
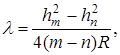
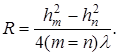
Таким образом, измерив величины хорд колец для монохроматического света с известной длиной волны 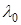
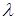
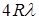
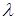
Измерения. Кольца Ньютона наблюдают при помощи поляризационного микроскопа МП-7.
1. Включают осветитель в сеть.
2. Сняв линзу, фокусируют микроскоп на верхнюю поверхность стеклянной пластинки, положив на нее кусок миллиметровой бумаги. Поставив затем линзу в прежнее положение, устанавливают пластинку так, чтобы точка соприкосновения линзы и пластинки попала в центр поля зрения микроскопа. При этом кольца Ньютона должны быть отчетливо видны. Если этого нет, то, не снимая линзу, исправляют фокусировку микроскопа до получения резкой картины. Если в точке соприкосновения вместо темного кольца будет светлое, то это значит, что между поверхностями линзы и пластинки имеется пыль, которую следует удалить при помощи замши.
3. Для измерения хорд применяют окулярный микрометр, позволяющий определить длину с точностью 0,01 мм . Вращая барабан окулярного микрометра, производят измерения величин хорд для всех колец (светлых и темных), начиная с 3-го, так как первые кольца широки и размыты. Вначале эксперименты проводят с зеленым светофильтром ( 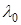
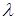
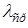
Примечание. В расчетах необходимо учесть увеличение, даваемое объективом микроскопа (применен объектив с увеличением х5,5). Измеренные хорды по барабану окулярного микрометра следует уменьшить в 5,5 раза.
Часть теории интерференции света дана в работе “Когерентность света”.
1. В чем заключается явление интерференции?
2. Какие источники называются когерентными? Пространственная и временная когерентности.
3. Почему преломляющий угол бипризмы должен быть малым?
3. Интерференционные полосы равного наклона и равной толщины в тонких пленках и их локализация.
4. Почему радиус кривизны линзы должен быть велик?
5. Вывести формулу (15).
6. Методы получения когерентных источников света.
Литература
1. Годжаев Н.М. Оптика. -М .: Высшая школа, 1977. с.67-116.
2. Сивухин Д.В. Общий курс физики. Т. IV . Оптика. – 3-е изд. Стереотип. – М.: ФИЗМАТЛИТ. 2005. С. 199-216, 247-249.
3. Матвеев А.Н. Оптика. -М .: Высшая школа, 1985, с.180-189.
4. Савельев И.В. Курс общей физики. — М.: Наука, 1971, Т.3, с.78-99.
5. Бутиков Е.И. Оптика: Учебное пособие. 3-е изд., доп. – СПб .: Изд. «Лань». 2012. С. 241-255.
Источник