ГЛАВА 6. ГРАФИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ
Рисунок – источник и душа каждого
изображения и корень каждой науки.
Микеланджело
Для описания движения тела часто используется графический язык, когда на некоторой координатной плоскости строятся графики зависимости одного кинематического параметра от другого. Наиболее часто используются графики зависимости координаты, скорости или ускорения тела от времени, хотя возможны и другие варианты, например, зависимость одной координаты тела от другой, или скорости от координаты и т.д. Такой способ описания является достаточно удобным и плодотворным, поскольку позволяет как «увидеть» все движение в целом, так и выделить его наиболее характерные особенности.
Рассмотрим несколько примеров, в которых содержатся основные принципы построения графиков движений или извлечения из этих графиков той или иной информации о движении тела.
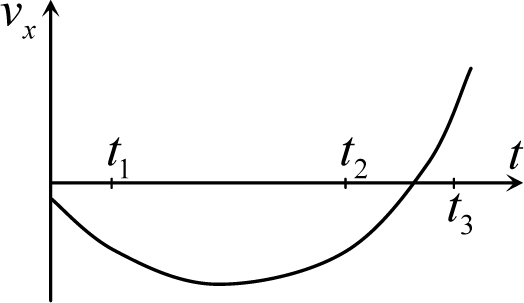
Пример 6.1. Тело движется прямолинейно вдоль некоторой оси x . На рис. 6.1 приведен график зависимости проекции скорости тела на ось x от времени. Сравнить проекции ускорения тела на ось x в моменты времени t 1 , t 2 и t 3 . Доказать, что на графике vx ( t ) не может быть разрывов.
Решение. Основная идея ответа на поставленный вопрос заключается в том, что мгновенному ускорению тела соответсвуют геометрические характеристики рассматриваемого графика. Для установления этого соответствия будем исходить из определения мгновенного ускорения в некоторый момент времени t :
Источник
Графический способ описания механического движения
Графическое представление равномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
V (t) — изменение скорости со временем
S(t) — изменение перемещения (пути) со временем
a(t) — изменение ускорения со временем

За висимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) — прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Так как тело движется прямолинейно и равномерно ( v = const ), т.е. скорость со временем не изменяется, то график с зависимостью скорости от времени v(t) — прямая линия, параллельная оси времени.
Проекция перемещения тела численно равна площади прямоугольника АОВС под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.
Зависимость перемещения от времени. График s(t) — наклонная линия :
Из графика видно, что проекция скорости равна:
Рассмотрев эту формулу, мы можем сказать, чем больше угол, тем быстрей движется тело и оно проходит больший путь за меньшее время.
Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Неравномерное прямолинейное движение.
Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.
Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным или переменным движением.
Для характеристики неравномерного движения вводится понятие средней скорости.
Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:
Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.
Различие между средней и мгновенной скоростями показано на рисунке.
Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.
Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:
Vx — Скорость тела при равноускоренном движении по прямой
Vx o — Начальная скорость тела
ax — Ускорение тела
t — Время движения тела
Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.
Единица измерения ускорения в СИ [м/с 2 ].
Ускорение измеряют акселерометром
Уравнение скорости для равноускоренного движения: vx = vxo + axt
Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):
Sx — Перемещение тела при равноускоренном движении по прямой
Vx o — Начальная скорость тела
Vx — Скорость тела при равноускоренном движении по прямой
ax — Ускорение тела
t — Время движения тела
Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:
— если известны начальная, конечная скорости движения и ускорение.
— если известны начальная, конечная скорости движения и время всего движения
Графическое представление неравномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
V(t) — изменение скорости со временем
S(t) — изменение перемещения (пути) со временем
a(t) — изменение ускорения со временем
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.
Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости vx = vxo + axt . Графиком является наклонная линия.
Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.
Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости:
В координатах зависимость имеет вид:
Источник
Способы описания движения

Средняя оценка: 4.6
Всего получено оценок: 218.
Средняя оценка: 4.6
Всего получено оценок: 218.
Кинематика – это раздел механики, изучающий движения тел вне зависимости от их причин. Для описания движения применяется ряд способов, обзор которых предлагается в данной статье.
Движение и его описание
Суть любого механического движения состоит в том, что тела меняют свое положение с течением времени. Главная задача кинематики состоит в том, чтобы находить это положение в любой указанный момент времени, как прошлого, так и будущего.
Для решения этой задачи движение необходимо описать так, чтобы описание выявляло закономерности, по которым происходит изменение положения тел. А дальше, задаваясь нужным моментом времени и сформулированным описанием – можно найти положение тела без непосредственного ожидания и измерения.
Таким образом, описание движения позволяет понять события, произошедшие в прошлом и будущем (иногда в далеком).
Способы описания движения
Любое описание движения заключается в том, чтобы найти связь между координатами тела в выбранной Системе Отсчета с моментами времени в этой же Системе. Если эта связь задана, то выбрав необходимый момент, можно получить координаты тела в это время.
Как можно задать связь между временем и координатой ? Имеется три способа описания механического движения.
Табличный способ
Исторически первым способом описания движения стал табличный. Он заключается в том, чтобы отмечать координаты тела в некоторые моменты времени. По представленному ряду пар «время – координата» мы можем видеть, в какие моменты прошлого тело двигалось быстрее, в какие медленнее, и когда где оно было.
Безусловно, такой способ самый грубый, поскольку моменты времени в таблице не обязательно будут равномерными, и, кроме того, таблица не дает представления о том, в каких точках находилось тело в моменты времени, не указанные в таблице. Однако, зачастую это и не требуется. Поэтому табличный способ описания движения до сих пор находит применение. В современных условиях для этого чаще всего используют стробоскопическую фотографию. Освещая тело в ряд моментов, можно зафиксировать положение тела в эти моменты.
Например, бросив тело с начальной высоты 2м вверх со скоростью 5м/с, и настроив стобоскоп на промежуток 0.2с, можно получить следующую таблицу, описывающую движение:
Время, с
Координата, м
Любое описания путешествий является таким табличным способом, поскольку везде, как правило, указывается ряд пар «место, где был путешественник – время, когда он туда прибыл».
Графический способ
Самым наглядным описанием движения является графический способ. Откладывая на оси абсцисс время, а на оси ординат расстояние – можно получить график, по которому положение тела в пространстве определяется в любой нужный момент. Кроме того, такой график дает наглядное представление о скорости изменения координаты.
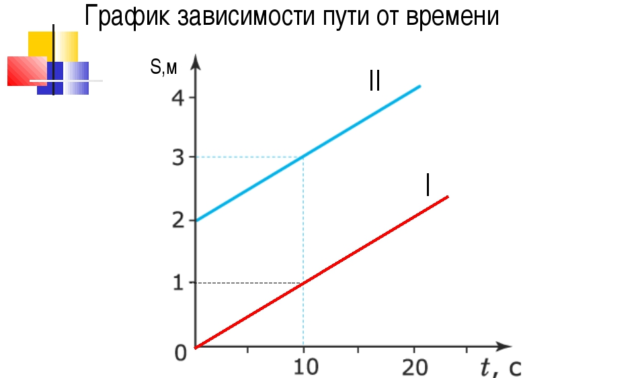
График зависимости координаты от времени ничего не говорит о траектории пути! График может быть прямой, а траектория – извилистой, и наоборот. Например, для случая, рассмотренного выше (тело, брошенное вверх), график координаты будет параболой. А траектория пути – прямой.
Аналитический способ
Наиболее полным и точным способом описания движения является аналитический, то есть, заданный математически.
Поскольку любая функция выражает зависимость, а описание движение и есть описание зависимости расстояния от времени – то во многих случаях данную зависимость можно выразить функцией. Задавшись такой функцией, и подставляя в качестве исходной переменной нужный момент времени – мы можем получить координату в этот момент.
Для примера, рассмотренного выше (тело, брошенное вверх), математическая функция, описывающая движение тела, выглядит следующим образом:
$$x(t) = 2 + 5t – 4.9t^2$$
Подставляя необходимый момент $t$, можно получить все значения из таблицы выше, а если надо – то и построить график зависимости расстояния от времени.
К сожалению, для большинства движений точное аналитическое описание слишком сложно (например, учет сопротивления воздуха сильно усложняет приведенную формулу). Однако, аналитический способ позволяет выделить наиболее важную компоненту движения, и описать ее наиболее удобным для дальнейшего использования образом.
Что мы узнали?
Описание движения устанавливает закономерности, с которыми тело меняло свое положение в пространстве. Они позволяют узнать положение тела в любой момент в прошлом, и спрогнозировать положение в будущем. Для описания движения применяется три способа: табличный, графический и аналитический.
Источник