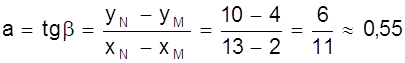Графический способ обработки данных

Графические методы обработки экспериментальных данных

Экспериментальные данные могут выражаться в виде таблиц, графиков, а также с помощью математических уравнений.

Табличный способ записи экспериментальных данных является наиболее простым и широко распространенным, полностью воспроизводит полученные результаты. Однако табличный способ менее наглядный по сравнению с графическим.

Графический метод позволяет наглядно оценить изменения переменных величин, установить характер этого изменения, а также с помощью этого метода можно без особых вычислений найти промежуточные значения переменных величин.

Кроме этого, графические методы обработки экспериментальных данных помогают вывести эмпирическую формулу в тех случаях, когда исследуемые процессы не подчиняются уже известным теоретическим законам. Тогда по экспериментальным данным устанавливается вид формулы и постоянные коэффициенты.

Табличный способ записи. В исследованиях по технологии бетона часто приходится определять зависимость между отдельными переменными величинами. При наличии возможности свободно задаваться численными значениями независимых переменных все опыты должны разбиваться на ряд серий с таким расчетом, чтобы в каждой серии одна из независимых переменных оставалась постоянной величиной. Например, необходимо найти зависимость между тремя переменными, из которых -искомая, В/Ц — изменение переменных в следующих пределах:

Для равномерного распределения значений переменных и В/Ц можно записать: для 5 значений, а для В/Ц — 7 значений.

Форма записи по переменной #ц будет иметь вид, приведенный в табл. 43.

Форма записи по перемещенной В/Ц будет иметь вид, приведенный в табл. 44.

Таким образом получили пять серий опытов, каждая при своем постоянном значении переменной, и семь опытов в каждой серии. При наличии таблицы можно на одном графике построить кривые зависимости неизвестной величины от переменной В/Ц при частных значениях переменной. При наличии таблицы легко построить график зависимости неизвестной от переменной при частных значениях переменной В/Ц. При наличии таких графиков легче подыскать и вывести зависимость между тремя переменными.

Выбор масштаба шкалы при построении графиков. При построении графической зависимости переменных величин пользуются равномерными и неравномерными шкалами. Равномерной шкалой при изображении функции в прямоугольных координатах называют такую, на которой расстояния между двумя делениями, соответствующими изменению переменной на одну и ту же величину, равны.

Если расстояния между двумя делениями, соответствующими изменению переменной на одну и ту же величину, не равны, такую шкалу называют неравномерной (логарифмической квадратичной шкалой и т. д.).

Масштабы по осям координат для равномерных шкал обычно принимают равными. Однако в некоторых случаях при значительной разнице в пределах изменения переменных величин не удается применить равные масштабы, тогда на осях координат применяют различные масштабы шкал, но обязательно с таким расчетом, чтобы построенные на этом графике кривые были наглядными и сам график получился бы наиболее компактным.

Применение различных масштабов шкал не сказывается на точности отсчетов, если на графике получается прямая линия, так как с изменением масштабов изменится лишь только ее наклон (черт. № 198).

Если же на графике получается кривая линия, то в этом случае при применении различных масштабов кривая будет искажаться, что может привести к снижению точности отсчетов и ввести в заблуждение исследователя при составлении выводов. Если на графике зависимости двух переменных величин получается кривая линия, следует пользоваться на обеих осях шкалами с равными масштабами.

Построение логарифмической шкалы основано на свойстве логарифмов, заключающемся в том,- что если любое число увеличить в 10, 100 и т. д. раз, то полученный логарифм нового числа, сохраняя свою мантиссу, увеличит только характеристику этого числа соответственно на 1, 2, 3 и т. д. Так, если 6 = 0,78, а 60= 1,78, то для получения отрезка, отвечающего 1д60, т. е. 1,78, нужно на оси отложить отрезок, равный 0,78, так как длина шкалы для значений х от 1 до 10 принимается равной единице (lg 10=1).

Для построения логарифмической шкалы берут две параллельные прямые и на одной из них (верхней) строят равномерную шкалу от 0 до 1. Затем определяют значения логарифмов целых чисел от 1 до 10, отмечают на верхней шкале точки, отвечающие значениям gx и переносят их на нижнюю прямую, записывая каждой перенесенной точке соответствующее значение х (черт. № 199). Логарифмическая шкала на осях координат позволяет спрямить получаемые кривые зависимости исследуемых величин и упрощает построение некоторых уравнений.

черт. № 198. Построение графика зависимости в прямоугольных координатах:

А — с равными масштабами шкал для прямой; б -с различными масштабами шкал для прямой; в — с равными масштабами шкал для кривой; г — с разными масштабами шкал для кривой

черт. № 199. Построение логарифмической шкалы функции длиной в два модуля

Источник

Графический метод обработки результатов

3.1. Графический метод обработки результатов

Графический метод заключается в построении графика зависимости между исследуемыми величинами с последующим определением уравнения зависимости между ними.

Графики строят прежде всего в равномерных шкалах. Если характер связи между исследуемыми величинами неизвестен, то сначала проверяют совпадение экспериментальных точек с заданной кривой. Если предварительные сведения о характере уравнения отсутствуют, то первым этапом обработки данных является нахождение кривой, совпадающей с опытными точками. Эта задача решается методом подбора. Можно использовать эталон — кальку с предварительно вычерченным на ней семейством кривых с различными параметрами. Естественно, что масштаб кальки и эмпирической кривой должен быть одинаков.

Построенный по опытным данным отрезок кривой может совпадать с большим количеством различных кривых, проходящих достаточно близко к опытным точкам. В этом случае выбирают кривую с наиболее простым и удобным в использовании уравнением. Иногда эмпирическая кривая может иметь перегибы или состоять из отдельных ярко выраженных участков. Однако при этом необходимо определить координаты точек перехода от одной кривой к другой.

Уравнение зависимости между исследуемыми величинами при графическом методе просто определяется тогда, когда эмпирические точки достаточно хорошо совпадают с прямой линией, т.е. описываются уравнением y = ax + b, где a, b — коэффициенты, подлежащие определению.

Определение коэффициентов при графическом методе основано на ²способе натянутой нити². Нанеся результаты эксперимента на график (лучше, если он выполнен на миллиметровке), подбираем графическую прямую, ближе всего подходящую к нанесенным точкам. Выбрав положение прямой, определяем две произвольные точки на этой прямой (не обязательно являющиеся точками эксперимента), определяем их координаты (x₁; y₁), (х₂; y₂). И для определения коэффициентов а и b получаем два простых уравнения

На рис. 10 приведена иллюстрация этого метода. Точки — результаты, полученные в эксперименте. Прямая проведена на глаз как можно ближе к экспериментальным точкам. На прямой выбраны точки М (2; 4) и N (13; 10). Коэффициент а характеризует угол наклона прямой.

.

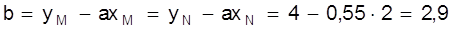
Таким образом y = 0,55х + 2,9.

Рис. 10. Графический метод интерполяции

В случае, если экспериментальная зависимость имеет нелинейный характер, то графическим способом в системе координат с равномерными шкалами определить коэффициенты кривой затруднительно. Но достаточно большой класс нелинейных зависимостей путем замены переменных и графического изображения в функциональных шкалах можно привести к линейным и далее использовать способ натянутой нити.

3.2. Функциональные шкалы и их применение

Пусть функция y = ¦(х) непрерывна и монотонна на некотором промежутке [ a; b ]. Возьмем ось ОМ, на которой будет строиться шкала, выберем на ней точку начала отсчета О и установим масштаб m. Функциональная шкала строится следующим образом.

Разбив интервал [ а; b ] на равные части, вычисляем значение функции ¦(х) в каждой из точек деления и отложим на оси ОМ для каждой точки отрезок m¦(х). Получающаяся при этом точка снабжается отметкой х, т.е. откладывается в выбранном масштабе значение функции, а надписывается значение аргумента.

Иногда начало шкалы помещают в первую точку отсчета, т.е. точку с надписью а совмещают с 0. Тогда точка х будет находиться в конце отрезка m [ ¦(х) — ¦(а) ]. Полученная шкала позволяет судить о поведении функции на рассматриваемом участке: большие промежутки между отметками укажут, что функция изменяется быстрее, чем там, где эти промежутки малы.

Выбор масштаба m определяет длину шкалы. Чаще поступают наоборот: задаются длиной шкалы l и определяют масштаб.

Þ m = .

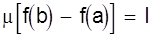
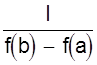
Пример. Построим функциональную шкалу для функции y = x 2 на участке [ 1; 2 ]. Зададимся длиной шкалы l = 12 см. Тогда m = 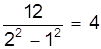см. Разобьем отрезок [ 1; 2 ] на десять равных частей и вычислим значения функции во всех точках деления. Совместим начало шкалы с точкой отсчета х = 1. Результаты расчета сведены в табл. 2, а функциональная шкала приведена на рис. 11.

Расчет функциональной шкалы y = x 2

х	1,0	1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9	2,0
1,0	1,21	1,44	1,69	1,96	2,25	2,56	2,89	3,24	3,61	4,00
0	0,21	0,44	0,69	0,96	1,25	1,56	1,89	2,24	2,26	3,00
0	0,84	1,76	2,76	3,84	5,00	6,24	7,56	8,94	10,44	12,0

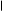1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0

Рис. 11. Функциональная шкала y = x 2

С помощью функциональных шкал графики многих функций могут быть преобразованы к прямолинейному виду.

Например, уравнение параболы y = x 2 . Если на оси OY нанести равномерную шкалу, а на оси OX₁ шкалу квадратов х₁ = х 2 , то получится сетка, где уравнение параболы имеет изображение прямой линии ( y = x₁ ),

проходящей через начало координат.

Особенно часто используются различные логарифмические функции, с помощью которых можно ²выпрямлять² графики степенных и показательных функций. Например, y = ae bx ; lg y = (b lg å) х + lg a. Полагая lg y = y₁, lg a = A, b lg e = B запишем исходное уравнение в виде y₁ = А + Вх, откуда видно, что оставив равномерной шкалу х и построив логарифмическую шкалу y₁, можно изобразить исходное уравнение прямой линией. Полученная координатная сетка называется полулогарифмической.

Очевидно, что такого рода преобразования возможны и в более общем случае. Всякая неявная функция, заданная соотношением вида

где a, b, с — постоянные, будет изображаться прямой линией на функциональной сетке, где на оси ОХ построена шкала j(х), а на оси OY — шкала функции y(y). Естественно, что функции j(х) и y(y) должны удовлетворять условиям непрерывности и монотонности. В табл. 3 приведены преобразования для некоторых функций.

Источник

Графические методы обработки данных

Графические редакторы. Широкий класс программ, предназначенных для создания и обработки графических изображений. Различают три категории: растровые редакторы (Adobe PhotoShop); векторные редакторы (CorelDraw); 3-D редакторы (трехмерная графика, 3D-Max).

В основе растровой графики лежит принцип точечного формирования изображения в ограниченных пространственных координатах без элементарных математических преобразований. Растровое изображение строится как совокупность отдельных точек, имеющих разный цвет. Если точки достаточно малы, то человеческий глаз воспринимает их как единое целое. Объекты изображения выделяются наблюдателем путем анализа изменений полутонов картины. Таким образом, без предварительного указания цвета точек изображения невозможно определить границы объектов, характеризующие их форму. Поскольку растровое изображение фактически является мозаикой из цветных точек, форма самой точки особой роли не играет. Главное для точки – ее цвет. Разрешение растрового изображения выражается количеством точек, приходящихся на единицу длины. Различают разрешение оригинала изображения, которое измеряют в точках на дюйм (dots per inch – dpi), и разрешение экранных и печатных копий изображений, которое измеряется в пикселях на дюйм (pixel per inch – ppi). Дюймовая система стала основной вследствие ее широко использования в сканирующей аппаратуре и в полиграфии.

Векторные редакторы позволяют создавать изображения из геометрических примитивов (точек, отрезков, дуг и многоугольников). Редактор векторной графики CorelDraw канадской фирмы Corel Corporation считается одним из лучших для векторной графики наряду с Adobe Illustrator, Deneba Canvas. Для векторной графики подошло бы утверждение «Цвет и форма независимы друг от друга, но форма первична, а цвет просто заполнитель формы». В векторном изображении базовым элементом является линия. Только замкнутая линия может быть заполнена цветом, текстурой или иным объектом, растровым или векторным. Таким образом, первой должна появиться линия (форма объекта), и лишь затем возможно изменение цвета. В векторной графике объект фактически является видимым отображением некоей хитрой формулы, описывающей этот объект. Следовательно, форма может существовать без визуального отображения, но при необходимости цвет «заливает» или «обводит» эту форму, проявляясь визуально. Например, в векторных редакторах может существовать объект, не имеющий ни заливки (заполнения), ни контура (абриса). Тогда он становится невидимым, но существует и может принимать участие в операциях с другими объектами.

Фрактал(от лат. fractus – дроблёный) – это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба. Базовым элементом фрактальной графики является математическая формула, задающая форму фигуры. Создание фрактального рисунка состоит в генерации изображений путем математических расчетов по данной формуле. Таким образом, понятия «цвет» и «форма» не существуют отдельно от уравнений для построения изображений фракталов. Данный вид графики по сути является гибридом векторной и растровой графики, где изображение есть визуальный образ некоей математической функции-формулы. Следовательно, форма не существует без способа описания цвета рисуемых элементов изображения.

Понятие трехмерной графики связано с возможностью моделирования в памяти компьютера объектов трехмерного пространства и не имеет отношения к описанию цвета.

Сканер является внешним периферийным устройством. Регистрацию растровых изображений в памяти компьютера осуществляют сканеры. Сканер является устройством, которое любой тип сканируемого носителя информации преобразует в растровое изображение. В дальнейшем данное изображение, фактически цифровую фотографию отсканированного объекта, можно с помощью специализированных программ преобразовать в текст, в векторное изображение либо работать с ним как с фотографией.

Основными характеристиками сканера являются пространственная разрешающая способность и количество передаваемых цветов. Первая количественно описывается числом различаемых точек на единицу длины, например «точек на дюйм», dot per inch (DPI). Вторая определяется разрядностью представления цвета одной точки. Современные значения – это 24 бита, 32 бита. Метод сканирования (планшетный, ручной, проекционный) не связан с качеством получаемых цифровых изображений. Даже большой по размерам лист документа может быть отсканирован с очень плохим качеством Размер цифрового изображения зависит от размеров сканируемого фрагмента и разрешающей способности сканера, т.е. зависит не только от свойств сканера.

Рассмотрим несколько примеров пересчета объема графического изображения на машинные единицы.

Пример 1. С помощью цифрового фотоаппарата получено изображение с разрешением 3456×2592 точек и глубиной цвета 3 байта/пиксель. Для просмотра используется монитор с установленными параметрами разрешения 1280×1024 и цветопередачей 16 битов. Определить, во сколько раз уменьшится информационный объем изображения при отображении его на этом мониторе.

Для подсчета необходимо учесть разрешение и глубину цвета у изображения и монитора, при этом находим отношение:

, где

8 – количество битов в 1-ом байте, т.к. 3 дана в байт/пиксель, а цветопередача в битах, необходимо привести к одним единицам.

Пример 2. Растровое изображение размером 64х64 пикселя занимает 4 килобайта памяти. Определить максимальное количество цветов, используемых в изображении.

Сначала узнаем, сколько битовых разрядов используется для кодирования цвета одного пикселя. Всего пикселей 64х64=4096. Объем памяти 4Кбайт=4096байт. Получается, что на кодирование цвета каждого пикселя отводится 1 байт памяти, т.е. 8 битов. Далее обращаемся к формуле Р. Хартли, связывающей количество двоичных разрядов (Y) для кодирования цвета с количеством цветов (N). . В нашем примере . Итак, каждый пиксель может иметь один цвет из 256.

Пример 3. Растровый графический файл содержит черно-белое изображение с двумя градациями цвета (черный и белый) размером 800х600 точек. Определить необходимый для кодирования цвета точек (без учета служебной информации о формате, авторстве, способах сжатия и пр.) размер этого файла на диске в байтах.

Поскольку сказано, что изображение двуцветное, следовательно, для указания цвета одной точки достаточно двух значений, кодирующих белый или черный цвет. Два значения могут быть закодированы одним битом. Объем графического файла рассчитывается по формуле V=i*k, где i – глубина цвета, а k – количество точек. Тогда объем графического файла равен 800*600*1бит=480000бит. Учитывая, что 8бит=1байт, получаем 480000/8=60000 байтов. В реальности в графических документах кроме описания цвета точек присутствует еще и служебно-дополнительная информация (о формате записи, авторских правах, способах сжатия и пр.).

Для наглядности рассмотрим работу с графическим редактором Paint.

Графический редактор Paint входит в состав ОС Windows, предназначен для построения несложных графических изображений.

Результат использования редактора:

1. Изображение на экране.

2. Изображение записанное на диск (в файл).

3. Изображение на листке бумаги, выведенное принтером.

Для запуска редактора выполнить:

Для завершения работы:

1. Кнопка

Для построения графических объектов необходимо предварительно выполнить следующие действия:

• Выбрать вид инструмента,
• Выбрать толщину линии (если такая возможность есть),
• Задать цвет фона и цвет линии,
• Используя эскиз, разбить изображение на отдельные простые графические элементы,
• Построить последовательно все простые графические элементы.

Рассмотрим простейшие операции:

Очистка экрана: \Рисунок\Очистить,

Задание цвета. Курсор мыши установить на кнопку нужного цвета «Палитры». Далее для задания цвета фона – ЩП, цвета линии – ЩЛ.

Распахнуть рабочее поле на весь экран: выполнить команду \Вид\Просмотреть рисунок. Возврат окна в исходное состояние – ЩЛ по любой точке окна.

а) Уменьшить размер изображения в окне:

Выход из режима «Закрыть».

б) Увеличить размер изображения в окне:

Выход из режима:

Теперь рассмотрим работу с панелью инструментов:

Карандаш(А4) – рисует линии выбранным в «окне цвета» цветом, рисует и правой и левой кнопкой.

Кисть (В4), в «окне дополнительных характеристик»:

Аэрозольный баллончик (А5) – распыляет правой и левой кнопкой, заданным цветом, в «окне дополнительных характеристик»:

Ластик (А2) – предназначен для стирания лишнего и не нужного, в «окне дополнительных характеристик»:

Изображение отрезка прямой:

Нажать кнопку А6

В окне дополнительных характеристик выбрать толщину линии.

Установить курсор на начальную точку отрезка и выполнить операцию ТиБ до конечной точки отрезка.

Для построения вертикальных и горизонтальных линий выполняйте операцию ТиБ с нажатой клавишей Shift.

Нажать кнопку А2

В «окне дополнительных характеристик» выбрать толщину ластика.

И выполнить операцию ТиБ от начала до конца стираемой полосы.

Помните, что ластик стирает (закрашивает) цветом фона.

Изображение прямоугольника (скругленного прямоугольника):

Нажать кнопку А7 (или В8).

В «окне дополнительных

характеристик» выбрать вид вид прямоугольника.

Задать цвет закраски прямоугольника (цвет фона) и цвет линии прямоугольника.

Установить курсор на верхний левый угол прямоугольника.

Выполнить операцию ТиБ по диагонали изображаемого прямоугольника.

Для построения квадрата эту операцию следует выполнять с нажатой клавишей Shift.

Изображение замкнутой ломаной линии (многоугольника):

Нажать кнопку В7.

В «окне дополнительных характеристик» выбрать вид многоугольника.

Задать цвета линии и заливки многоугольника.

Установить курсор в начало первого отрезка и выполнить операцию ТиБ до конца первого отрезка.

Повторить эту операцию для всех отрезков многоугольника, пока линия не замкнется.

Изображение окружности или эллипса:

Нажать кнопку A8.

В «окне дополнительных характеристик» выбрать вид эллипса.

Выбрать цвет линии и заливки.

Мысленно наметить в окне квадрат (прямоугольник) в который должна быть вписана наша окружность (эллипс).

Установить курсор в верхний левый угол этого квадрата (прямоугольника).

Выполнить операцию ТиБ по диагонали нашего квадрата (прямоугольника).

Заметим, что для построения окружности данную операцию надо выполнять с нажатой клавишей Shift.

Закрашивание области ограниченной замкнутым контуром:

Нажать кнопку В2.

Выбрать цвет заливки.

ЩЛ (ЩП) по любой точке внутри контура.

Заметим, что если контур не замкнут, произойдет заливка всего рисунка, даже если контур не замкнут всего на размер одного пикселя.

Изображение дуги. Редактор позволяет за один прием построить не только одну дугу, но и две сопряженных:

Нажать кнопку В6.

В «окне дополнительных характеристик» выбрать толщину линии.

Задать цвет дуги.

Выполнить операцию ТиБ от начальной точки дуги до конечной.

На экране появится отрезок.

Теперь переместить курсор на середину отрезка и выполнить операцию ТиБ.

Если надо закончить изображение дуги то сделайте ДЩ левой кнопкой мыши.

Для продолжения рисования сопряженной дуги, переместите курсор по уже полученной дуге и вновь выполните операцию ТиБ. Получим следующую картинку:

Подбор цвета из имеющегося графического изображения.

Эта операция необходима при редактировании уже готовых картинок или фотографий.

Если вам необходимо подобрать цвет для редакции, а в вашей палитре его нет, зато он есть на самом рисунке, тогда

Нажмите клавишу А3.

Установите курсор в том месте рисунка, где есть нужный цвет и выполните ЩЛ.

Построение произвольных фигур при помощи карандаша (кисти):

Нажать кнопку А4 (В4).

В «окне дополнительных характеристик» выбрать толщину линии.

Выбрать цвет линии.

При помощи операции ТиБ нарисовать нужную фигуру.

Построение произвольных фигур при помощи аэрозольного баллончика:

Нажать кнопку А5.

В «окне дополнительных характеристик» выбрать плотность струи баллончика.

Непосредственно произвести рисование.

Вывод текста на экран:

Нажмите кнопку В5.

Курсор мыши установите на начало текста и выполните ЩЛ.

С помощью панели инструментов «Шрифты» выберите настройки текста. (Если панели инструментов не появляется, то откройте ее при помощи \Вид\Панель атрибутов текста)

Теперь можно набрать текст.

Работа в режиме лупы. В этом режиме можно увидеть любой фрагмент текста в увеличенном виде и работать с пикселями.

Нажмите кнопку В3.

Наведите прямоугольник с лупой на нужный фрагмент картинки и выполнить ЩЛ.

Для возвращения в исходное состояние:

Нажмите кнопку В3.

Выполните ЩЛ по любому фрагменту рисунка.

Выделение прямоугольного фрагмента изображения:

Нажмите кнопку В1.

Установите курсор мыши в верхний левый угол прямоугольника выделения.

Выполните прием ТиБ по диагонали прямоугольника выделения.

Выделение произвольного фрагмента изображения:

Нажмите кнопку А1.

Установите курсор мыши в начало выделения.

Выполните прием ТиБ произвольной замкнутой линией внутри которой окажется нужный фрагмент рисунка.

Переместить фрагмент изображения:

— Установить курсор на выделенный фрагмент.

— Выполнить прием ТиБ, пока фрагмент не встанет на нужное место.

— ЩЛ вне фрагмента отменит выделение.

4. Копирование фрагмента изображения выполняется также как и перемещение, только прием ТиБ выполняется с нажатой клавишей Ctrl.

5. Изменить размеры фрагмента (по высоте и ширине):

— установить курсор мыши на маркер рамки

он примет вид:

— применить прием ТиБ для изменения фрагмента изображения.

6. Записать фрагмент изображения на диск:

— \Правка\Копировать в файл…

7. Вставить в окно редактора фрагмент записанный в файл:

— \Правка\Вставить из файла

фрагмент появляется в верхнем левом углу рисунка.

— Приемом ТиБ переместить фрагмент в нужное положение.

8. Преобразование фрагментов (вращение, наклон, пропорциональное изменение):

8а. Зеркальное отражение фрагмента:

8б. Обратим цвета при помощи:

8в. Наклоним фрагмент при помощи:

8г. Изменим размеры рисунка при помощи:

9. Печать изображе-ния:

— подготовить принтер для печати;

— вывести изображе-ние на экран;

— выполнить команду \Файл\Предварительный просмотр и оценить размещение рисунка;

— выполнить: \Файл\Параметры страницы и задать параметры страницы;

С помощью кнопки «Настройка» вы можете настроить расход чернил (порошка), вид бумаги т. д.

Сохранить полученное изображение:

— \Файл\Сохранить или \Файл\Сохранить как

Загрузить изображение из файла:

Презентация PowerPoint

Презентация в PowerPoint XP– система , состоящая из множества слайдов , своеобразных страниц, которые оформлены и заполнены пользователем.

Источник