Графический способ моделирования при решении задач

Решение задач методом графического моделирования
статья по математике (3 класс) на тему

Для того чтобы решить задачу, необходимо построить ее математическую модель, а затем применить известные методы для нахождения числового значения искомых величин.

Условное изображение предметов, взаимосвязей между ними и взаимоотношения величин с помощью отрезков и с соблюдением определенного масштаба называется схематическим чертежом, или схемой.

Текст любой сюжетной задачи можно представить графически. Это и есть переход от словесного моделирования к другим формам моделирования.

Скачать:

Вложение	Размер
Для того чтобы решить задачу, необходимо построить ее математическую модель, а затем применить известные методы для нахождения ч	17.5 КБ

Предварительный просмотр:

Решение задач методом графического моделирования

Формирование умения решать задачи является одной из основных целей обучения математике в начальной школе.

При обучении решению текстовых задач необходимо достигнуть двух взаимосвязанных целей — обучить:

1) решению определенных видов задач, что важно потому, что дает необходимый опыт и возможность выделить в решаемой задаче те подзадачи, решение которых известно. Кроме того, при решении каждой новой задачи можно использовать уже знакомые способы и приемы,

2) приемам поиска решения любой задачи , так как на практике приходится встречаться с задачами, при поиске решения которых никакой прежний опыт не помогает и требуется догадка, «открытие».

Можно ли помочь ученику прийти к такой догадке, дать ему некоторое средство, помогающее «открытию» ?

Для того чтобы решить задачу, необходимо построить ее математическую модель, а затем применить известные методы для нахождения числового значения искомых величин.

Условное изображение предметов, взаимосвязей между ними и взаимоотношения величин с помощью отрезков и с соблюдением определенного масштаба называется схематическим чертежом, или схемой.

Текст любой сюжетной задачи можно представить графически. Это и есть переход от словесного моделирования к другим формам моделирования.

Для построения модели любой сюжетной задачи необходимо выделить в задаче цель, данные величины, зафиксировать все отношения, чтобы с опорой на эту модель можно было продолжить анализ , позволяющий составить план и искать оптимальные пути решения.

Опираясь на чертёж, легко можно дать ответ на вопрос задачи. Графический способ даёт возможность более тесно установить связь между арифметическим и геометрическим материалами, развить функциональное мышление детей.

Благодаря применению графического способа в начальной школе можно сократить сроки, в течение которых ученик научится решать различные задачи. В то же время умение графически решать задачу — это важное политехническое умение.

Графический способ даёт иногда возможность ответить на вопрос такой задачи, которую дети ещё не могут решить арифметическим способом.

Графическая информация легче для восприятия, более ёмкая, и, вместе с тем, может быть достаточно условной.

Рисование графической схемы,

во-первых , заставляет ученика внимательно читать текст задачи,

во-вторых, позволяет перенести часть умственных действий в действия практические и закрепить результат в виде материального объекта,

в-третьих, дает возможность искать решение самостоятельно.
Для этого необходимо с первого класса учить детей разбивать текст задачи на смысловые части и моделировать ситуации, отраженные в задаче.

Систематическое использование графического моделирования обеспечит более качественный анализ задачи, осознанный и обоснованный выбор необходимого арифметического действия и предупредит многие ошибки в решении задач учащимися.
Таким образом, чтобы дети лучше представляли себе жизненную ситуацию, отраженную в задаче, легче прослеживали зависимости между величинами, а выбор действия становился для них осознанным и доказательным, необходимо систематически обучать детей моделированию, начиная с полного предметного изображения числового взаимоотношения величин с демонстрацией самого действия задачи.

Затем следует переходить к более обобщенному условно-предметному и графическому моделированию, к краткой записи задачи с использованием создаваемого на глазах у детей и самими детьми чертежа, схемы, после чего можно переходить к более высокой степени абстракции с применением готовых обобщенных опорных схем и таблиц .

Мультимедийный материал помогает иллюстрировать работу над задачей.

Данную презентацию можно использовать в качестве наглядной демонстрации при изучении задач в 1 классе. Анализ условия задачи дополнен анимированным рисунком и схемой, есть запись решения и ответ для самопроверки.

Читаем задачу с доски, анализируем, выбираем главные слова. Щелчок компьютерной мышки подчеркивает главные слова красной линией. Далее последовательно по щелчкам появляется наглядное изображение к задаче – рисунок и схема.

В работе подобраны задачи всех типов, с которыми знакомятся учащиеся 1-х классов. Эти задачи можно использовать в начале 2-го класса на уроках повторения. По аналогии можно составить тексты других задач.

Переход с главного слайда ( слайд 2) на слайды с задачами осуществляется кликом мыши по кнопке «карандаш».

Переход с любого слайда на главный слайд с содержанием осуществляется кликом мыши по управляющей кнопке «карандаш».

Источник

Графическое моделирование текстовых задач на уроках математики в начальной школе.

В методической разработке раскрывается роль моделирования при решении текстовых задач по математике. Исследуется применение различных вспомогательных моделей для правильного анализа и решения задач. Показано, какое образовательное, воспитательное, практическое значение имеет графическое моделирование при обучении решению текстовых задач

Просмотр содержимого документа
«Графическое моделирование текстовых задач на уроках математики в начальной школе.»

Муниципальное автономное общеобразовательное учреждение

«Светлинская средняя общеобразовательная школа №2»

Графическое моделирование текстовых задач

на уроках математики в начальной школе

Головиной Оксаны Иосифовны,

учителя начальных классов

МАОУ «Светлинская СОШ №2»

Моделирование – процесс построения моделей

для познавательных целей……………………………………… 5

Психологический аспект использования моделирования

на уроках математики…………………………………………… 6

Графические модели текстовых задач…………………………. 7-8

Развивающая роль графического моделирования

в обучении математике………………………………………….. 9

2.1 Графическое моделирование: этапы работы………………… 10-12

2.2 Применение графического моделирования

при решении текстовых задач……………………………….. 13- 17

Современная система образования, в том числе стандарты второго поколения, ориентированы на подготовку обучающихся к самостоятельному активному освоению мира, его творческому преобразованию, поэтому одним из важнейших направлений педагогики сегодня является формирование личности школьника, способной творчески освоить сложности жизни. Различные аспекты этой темы рассматриваются в трудах ученых: Л. Выготского, В.П. Зинченко, Д.С.Лихачева и других. Формирование личности – это последовательное изменение и усложнение системы отношений к окружающему миру, природе, труду, другим людям и к себе. Именно в детском возрасте в личности закладываются важнейшие ее качества, и происходит «переход психологии научения к психологии решения задач».

ФГОС начального общего образования выдвигает новые требования к подготовке младшего школьника. Особого внимания заслуживает направление, связанное с формированием метапредметной готовности учащихся, которая предполагает овладение компетенциями, составляющими основу умения учиться. К подобным компетенциям относится способность применять различные средства представления информации для создания моделей изучаемых объектов и процессов, схем решения учебных и практических задач. Таким образом, можно вести речь о целенаправленном развитии у учащихся умений, связанных с применением моделей и моделирования. Очевидно, что именно математика обладает тем потенциалом, благодаря которому эти умения формируются и совершенствуются.

Решение текстовых задач – важная составляющая курса математики начальной школы. Умение решать текстовые задачи является одним из основных показателей уровня математического развития младшего школьника. Однако практика показывает, что решение текстовых задач представляет большие трудности для обучающихся, так как дети не все хорошо ориентируются в тексте задачи, в ее условии и требовании.

Как же действовать в этой ситуации учителю? Приёмом, позволяющим научить детей решению текстовых задач, является метод моделирования. Мы считаем, что система работы над текстовыми задачами методом моделирования открывает новые возможности для развития интереса к математике, логического мышления младших школьников. На необходимость использования моделирования в учебной деятельности указали в своих работах психологи П.Я.Гальперин, В.В.Давыдов, Л.В Занков, Н.И.Непомнящая и др.

В Федеральном Государственном образовательном стандарте начального общего образования во главу угла поставлено формирование универсальных учебных действий, обеспечивающих школьникам умение учиться, способность к саморазвитию и самосовершенствованию. Младший школьный возраст является началом формирования учебных действий у детей. Особую группу общеучебных универсальных действий составляют знаково-символические действия, которые обеспечивают конкретные способы преобразования учебного материала, представляют действия моделирования, выполняющие функции отображения учебного материала; выделения существенного; отрыва от конкретных ситуативных значений; формирования обобщенных знаний. Это действия:
— моделирование – преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта (пространственно-графическую или знаково-символическую);

— преобразование модели – изменение модели с целью выявления общих законов, определяющих данную предметную область.

Для того чтобы вооружить учащихся моделированием как способом познания, нужно, чтобы школьники сами строили модели, сами изучали какие-либо объекты, явления с помощью моделирования. Известно несколько видов моделирования. Чтобы сузить рамки содержания темы, остановимся на одном из них – графическом моделировании.

Целью работы является разработка системы приемов графического моделирования и применение этих приёмов в практике учебной работы.

Рассмотреть графические модели, включить их в практическую работу с детьми;

Подобрать различные виды упражнений по обучению графическому моделированию

Систематизировать приемы графического моделирования, учитывая опыт учителей начальной школы.

мыслительную активность детей мыслительную активность детей мыслительную активность дете,

1.1 Моделирование – процесс построения моделей для познавательных целей

В методической науке существуют разные определения моделирования. «Моделирование – процесс построения моделей для каких-либо познавательных целей. Модель – это объект или система, исследование которой служит средством для получения знаний о другом объекте – оригинале». (Л.М.Фридман, К.Н.Волков)

В философском энциклопедическом словаре моделирование рассматривается как метод познания. Его сущность заключается в следующем: для познания объекта строятся и изучаются модели этого объекта, отображающие реальность. [13]

И.Б. Новиков дает следующее определение: «Моделирование – практическое или теоретическое исследование объекта. При исследовании непосредственно изучается не интересующий нас объект, а вспомогательная искусственная или естественная система, находящаяся в некотором объективном соответствии с познаваемым объектом, способная его замещать в определенном отношении и дающая при его исследовании, в конечном итоге, новую информацию о самом моделируемом объекте».

В школьной практике изучения математики моделирование применяется достаточно широко. Но об этом будет сказано ниже.

Моделирование – это действие, которое выносится и за пределы младшего школьного возраста и в дальнейшие виды деятельности человека и выходит на новый уровень своего развития. С помощью моделирования можно вести изучение от простого – к сложному, от незнакомого — к знакомому, то есть сделать объект доступным для тщательного изучения.

Какую же практическую пользу принесёт обучающимся овладение методом моделирования?

Во-первых, введение в содержание обучения понятий модели и моделирования существенно меняет отношение учащихся к учебному предмету, делает их учебную деятельность более осмысленной и более продуктивной, приводит к ощущению успешности.

Во-вторых, целенаправленное и систематическое обучение методу моделирования приближает младших школьников к методам научного познания, обеспечивает их интеллектуальное развитие.

В-третьих, моделирование является средством развития логического мышления обучающихся, повышает мыслительную активность.

1.2 Психологический аспект использования моделирования

на уроках математики

Психология, изучая действия человека, направленные на познание окружающего мира, рассматривает моделирование с позиции познающего субъекта. С этой точки зрения графическое моделирование рассматривается как процесс или деятельность субъекта по построению графической модели для одной из определённых целей, а именно с целью замещения, представления, интерпретации, исследования объекта изучения. Модельное отношение тогда является тройственным. В него входят оригинал, его модель и субъект, выбравший или построивший эту модель. Появление субъекта, или исследователя, в сложной структуре процесса моделирования в какой-то мере предопределило развитие моделирования как содержания и средства обучения.

Психологами доказано, что моделирование имеет принципиальное значение для учебной деятельности. Важнейшим результатом психологических исследований для методической науки стал вывод о том, что уже в младшем школьном возрасте дети способны выполнять действие моделирования с целью изучения данных им объектов. Всевозможные аспекты процесса применения моделирования рассматривались на разных этапах развития начального образования. Однако графическое моделирование преимущественно связывали с проблемой обучения решению текстовых задач. Овладевая графическим моделированием, учащиеся овладевают подходами к решению текстовых задач.

1.3. Графические модели текстовых задач

Текстовая задача – это словесная модель проблемной ситуации. Чтобы решить задачу, надо перевести ее на язык математических действий, т.е. построить математическую модель. Математической моделью текстовой задачи является выражение (либо запись по действиям или уравнение) если Перевод текста с естественного языка на математический – сложный процесс. Чтобы облегчить его – строят вспомогательные модели. Тогда процесс решения задачи можно рассматривать как переход от одной модели к другой: от словесной модели к вспомогательной, от нее – к математической, на которой и происходит решение задачи. Математическая модель – это описание какого–либо реального процесса на математическом языке. [10]

Такой подход к решению задач разделяют психологи. Они считают, что процесс решения задач – это процесс поиска системы моделей. Каждая модель выступает как одна из форм отражения сущности задачи, а преобразование ее идет по пути постепенного обобщения, абстрагирования и, в конечном счете, построение ее математической модели. Итак, чтобы решить задачу, т.е. перейти к ее математической модели, необходимо построить промежуточную – вспомогательную модель.

Вспомогательная модель – это и есть графическая модель. Под графической моделью можно понимать такое реализованное с помощью графического действия изображение, которое не только воспроизводит объект исследования, его отдельные свойства и отношения, но и позволяет осуществить их дальнейшее изучение.

В структуре любой задачи выделяют:

1. Предметную область, т. е. объекты, о которых идет речь в задаче.

2. Отношения, которые связывают объекты предметной области.

3. Требование задачи.

Объекты задачи и отношения между ними составляют условие задачи. Напри­мер, в задаче:

«Лида нарисовала 5 домиков, а Вова — на 4 домика больше. Сколько домиков нарисовал Вова?» — объектами являются:

1) количество домиков, нарисованных Лидой (это известный объект в задаче); количество домиков, нарисованных Вовой (это неизвестный объект в задаче и согласно требованию искомый).

2) Связывает объекты отношение «больше на».

Структуру задачи можно представить с помощью графических моделей

Рассмотрим некоторые виды графических моделей на примере одной задачи.

«Катя нарисовала 5 деревьев, а Вова – на 3 дерева больше. Сколько нарисовал Вова?».

У словный рисунок: К.

В.

К. 3д.

В.

К.

В.

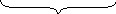
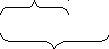
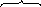
Наибольшую сложность в процессе решения текстовой задачи представляет перевод текста с естественного языка на математический. Чтобы облегчить эту процедуру, строят вспомогательные модели – схемы, таблицы и другие. Тогда процесс решения задачи можно рассматривать как переход от одной модели к другой: от словесной модели реальной ситуации, представленной в задаче, к вспомогательной (схемы, таблицы, рисунки и так далее); от неё – к математической, на которой и происходит решение задачи.

Как отмечает Л.Ш. Левенберг, «… рисунки, схемы и чертежи не только помогают учащимся в сознательном выявлении скрытых зависимостей между величинами, но и побуждает активно мыслить, искать наиболее рациональные пути решения задач, помогает не только усваивать знания, но и овладевать умением применять их».

Для графических моделей характерны следующие особенности:

– наглядность данных моделей;

– возможность сохранять информацию для дальнейшего изучения и преобразования;

– организация внутренней психической деятельности учеников;

– указание способов организации действий учащихся;

– открытие нового знания, скрытого при поверхностном анализе объекта исследования.

1.4. Развивающая роль графического моделирования

в обучении математике

Рассмотрение теоретических основ применения графических моделей в обучении математике позволяет не только ещё раз подчеркнуть их роль в развитии младших школьников, но и помогает выделить некоторые условия использования графического моделирования как содержания и средства обучения. Среди них:

– систематическая и целенаправленная подготовка учащихся к моделированию;

– применение моделирования при решении широкого круга математических задач на различных этапах усвоения математического содержания;

– формирование у школьника осмысленного отношения к моделированию, в котором он как исследователь играет главную роль, выбирая средство для построения модели, определяя цель применения, интерпретируя результаты изучения модели;

– преимущественное использование учебных заданий на сопоставление, создание, преобразование, исследование, интерпретацию моделей, а также открытие новой информации, неявно представленной в условии математической задачи.

Начиная с первых дней обучения в школе, ученикам систематически предлагаются задания, в процессе выполнения которых у них постепенно накапливается опыт перевода обычного текста и аналитических выражений на язык графических изображений и обратно. Только в этом случае графические модели могут стать эффективным средством обучения решения задач с использованием моделирования. Из сказанного не следует, что при решении каждой задачи обязательно нужно строить графическую модель. Она является вспомогательным средством, и ее использование ни в коем случае не должно вести к ослаблению работы по формированию умения решать задачи с помощью логических рассуждений, проводимых и без опоры на непосредственное зрительное восприятие графического изображения.

На современном этапе образования под развивающим обучением понимается обучение младших школьников общим приемам умственной деятельности, а на уроках математике – общим приемам по усвоению математических понятий. Данный процесс можно реализовать в традиционной системе обучения при решении математических задач, используя метод моделирования. Он дополняет учебную работу школьников поисковой деятельностью, помогает формированию таких приемов умственной деятельности как абстрагирование, анализ, синтез; развивает математическое мышление. Моделирование задач позволяет младшим школьникам подняться на достаточно высокую ступеньку абстрактности: все второстепенные детали опущены, выбор действия производится только из логики происходящих изменений.

Глава II

2.1. Графическое моделирование: этапы работы

За основу взят УМК «Школа России» (программа по математике М.И. Моро, М..А. Бантовой, Г.В. Бельтюковой). Важным является усовершенствование общих приемов умственной деятельности (наблюдения, анализа, сравнения, синтеза, обобщения, дедуктивному и индуктивному умозаключению и т.д.). Мною также анализировались учебники Н.Б. Истоминой (УМК «Гармония»), И.И. Аргинской (развивающая система Л.В. Занкова), Л.Г. Петерсон (УМК «2000»). Заложенная в них концепция целенаправленной и систематической работы по формированию приемов умственной деятельности: анализа и синтеза, сравнения, классификации, аналогии и обобщения в процессе усвоения математического содержания показалась мне очень важной для любого ребенка, с какой бы математической подготовкой он не пришел бы в первый класс и по какой бы системе не обучался.

Графическое моделирование заключается в том, что для исследования какого-либо объекта (в нашем случае текстовой задачи) выбирают (или строят) другой объект, в каком-то отношении подобный тому, который исследуют. Построенный новый объект изучают, с его помощью решают исследовательские задачи, а затем результат переносят на первоначальный объект.

В графическом моделировании выделяется ряд этапов:

предварительный анализ текста задачи;

перевод текста на знаково-символический язык, который осуществляеся графическими средствами;

работа с моделью;

соотнесение результатов, полученных на модели, с реальностью (с текстами).

Каждый компонент деятельности моделирования имеет свое содержание со своим составом операций и средствами, которые согласно психологическим исследованиям должны стать самостоятельным предметом усвоения.

Предварительный анализ включает ряд приемов. Это прежде всего проведение семантического анализа текста. Он предполагает работу над отдельными словами, терминами, перефразирование, переформулирование текста. Другим приемом анализа текста, ведущего к пониманию его смысла, являются постановка вопросов, определенный способ чтения текста. В литературе выделена система вопросов, ведущих к осмыслению текста. Одним из приемов анализа, ведущих к пониманию текста, является выделение «смысловых опорных пунктов» текста, которые способствуют выделению структуры текста.

В общей деятельности моделирования действие анализа является подготовительным этапом для осуществления действия перевода и построения модели.
Для приобретения опыта в семантическом и математическом анализе текстов задач (простых и составных) используются следующие задания (Приложение 1)

Эти задания позволяют школьникам сделать первые шаги в ос­мыслении структуры задачи.

Перевод текста на знаково-символический язык делает обозримыми связи и отношения, скрытые в тексте, и способствует тем самым поиску и нахождению решения. Эффективность перевода текста определяется видом используемых знаково-символических средств.

При создании различного типа моделей очень важно выделить, какая информация должна быть включена в модель, какие средства (символы, знаки) будут употребляться для каждой выделенной составляющей текста, какие из них должны иметь одинаковую символику, а какие – различную. В процессе построения модели и работе с ней проводится анализ текста и перевод на математический язык: выделяются известные, неизвестные объекты, величины, отношения между ними, основные и промежуточные вопросы.
Построению графической модели следует специально учить детей.

Для этого можно использовать следующую «Памятку» (Приложение 2).

Чтобы проверить, все ли данные задачи отражены на модели, можно прочитать задачу, показывая, все на модели.

Работа с моделью. Вынесение во внешний план элементов задачи и их отношений, настолько обнажает связи и зависимости между величинами в задаче, что иногда перевод сразу ведет к открытию решения. Однако во многих задачах перевод текста на язык графики является только началом анализа, для решения задачи требуется дальнейшая работа со схемами. Именно здесь возникает необходимость формирования у учащихся умения работать с моделями, преобразовывать их. При этом необходимо иметь в виду, что уровень графической подготовки при построении модели и работе с ней (согласно психологическим исследованиям) определяется главным образом не степенью владения им техникой выполнения графического изображения, а тем, насколько он готов к мысленным преобразованиям образно-знаковых моделей, насколько подвижно его образное мышление.

Работа с моделью может вестись в двух направлениях:

а) достраивание схемы, исходя из логического выведения, расшифровки данных задачи;

б) видоизменение схемы, ее переконструирование.
В процессе обучения графическому моделированию можно использовать следующие задания и вопросы (Приложение 3)

Наряду с выше изложенным, учитель должен помнить, что одного составления модели к задаче недостаточно. Следует включить и обратные задания, а именно: составление текстов различных задач по модели, на выбор нужной модели к данной задаче, на нахождение ошибок в модели и др., что будет способствовать развитию творческого мышления каждого ребенка (Приложение 4).

Постоянное использование этих заданий дает хорошие результаты, способствует формированию умения решать задачи.

Соотнесение результатов работы на модели с текстом.

Моделирование осуществляется для того, чтобы получить новые данные о реальности или ее описании, поэтому необходимым моментом деятельности моделирования является соотнесение результатов с текстом.

Из практики известно, что учащиеся после решения задачи так или иначе проверяют свои ответы для доказательства того, что полученные ответы удовлетворяют условиям и требованиям задачи. Однако это соотнесение результатов с текстом задачи не есть только проверка ответа задачи, соотнесение его с требованиями. Принципиально важным при проверке ответов решения задачи для деятельности моделирования является не столько выявление правильности (точности) ответа, сколько соотнесение данных, полученных на модели с ее описанием в тексте.

На уроках использую модель работы над задачей по системе Занкова (Приложение 5)

Графическое моделирование – это замена действий с обычными предметами действия с их уменьшенными образцами, моделями, муляжами, макетами, а также их графическими заменителями: рисунками, чертежами, схемами и т.п.

Но чтобы получить желаемый результат, надо помнить:

Работа должна быть систематической;

Модель должна возникать на глазах детей;

Необходимо поощрять желание детей выполнить краткую запись;

Проверять правильность выполнения модели;

Сравнивать разные способы, выявлять рациональный.

Применение графического моделирования при решении текстовых задач

Уровень опыта по степени новизны состоит в комбинировании элементов известных методик (опорные схемы С.Н. Лысенковой, технология развивающего обучения Л.В. Занкова, графическое моделирование из системы Н.Б.Истоминой).

Рассмотрим, как можно использовать метод моделирования при решении задач.

Р абота по моделированию начинается с 1 класса. Сначала задачи моделируются с помощью рисунков и схематических рисунков.

«У мальчика было 3 красных мяча и 2 синих. Сколько всего мячей было у мальчика?»

« У Маши было 6 яблок. Она отдала Тане 2 яблока. Сколько яблок осталось у Маши?»

«В первый день для ремонта школы привезли на 4-х машинах по 10 бревен. Сколько всего бревен привезли за эти два дня?» Если записать ее кратко в таком виде:

2д. — на 4 маш. по 10б.

Такая модель не отражает жизненной ситуации с достаточной наглядностью, что приводит к ошибкам в решении задачи. Поэтому необходимо смоделировать ее условие в виде схематического рисунка:

Такая модель отражает математическую ситуацию более наглядно. По ней даже слабый ученик сможет записать решение, если не так:

28 + 10 * 4 = 68 (б.), то хотя бы так:

Ответ: 68 бревен.

«В совхозе работают 37 трактористов, шоферов на 8 больше, чем трактористов, а комбайнеров на 5 меньше, чем шоферов. Сколько комбайнеров работает в совхозе?» Обычная краткая запись этой задачи выглядит так:

Ш. — на 8 больше, чем трактористов

К. — ? — на 5 меньше, чем шоферов

Такая запись при первичном анализе этой задачи нерациональна, так как не раскрывает наглядно взаимоотношении величин и не помогает в выборе действий.

На уроке с учениками мы смоделировали задачу по другому.

Такая модель дает наглядное представление об отношениях между данными и искомыми в задаче. Анализируя задачу, дети выясняют, что шоферов на 8 больше, чем трактористов, т.е. их столько же да еще 8. поэтому отрезок на схеме, изображающий численность шоферов, они начертят большей длины, чем отрезок, изображающий численность трактористов. А так как численность комбайнеров на 5 меньше, чем шоферов, т.е. их столько же, но без 5, то и отрезок, показывающий численность комбайнеров, должен быть меньше отрезка, показывающего численность шоферов. При таком моделировании выбор действия будет понятным и обоснованным.

«В трех одинаковых ящиках 21 кг апельсинов. Сколько килограммов апельсин в 8 таких ящиках?»

Источник