Графический или геометрический способ

Геометрический способ задания графов

Множество элементов V графа G изображают кружками, это множество вершин. Каждую вершину соединяют линиями с теми вершинами , для которых выполняется условие Множество линий, которое соответствует множеству упорядоченных пар есть множество рёбер.

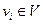
Матричный способ задания графов

Квадратная матрица элементами которой являются нули и единицы, а также некоторое число m, называется матрицей смежности графа тогда и только тогда, когда её элементы образуются по следующему правилу: элемент стоящий на пересечении й строки и го столбца, равен единице, если имеется ребро, идущее из вершины в вершину и равен нулю в противном случае. Элемент равен единице, если при вершине имеется петля, и равен нулю в противном случае. Элемент равен некоторому числу m, где m – число рёбер графа, идущее из вершины в вершину

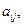
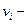
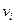
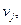
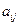
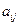
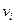
Таким образом, если граф задан одним из указанных способов: аналитическим, геометрическим или матричным, всегда можно перейти к любому другому способу задания. Наиболее часто для задания графа используется аналитический и матричный способы, а геометрический способ служит для иллюстрации полученных результатов.

Инструкция к практической работе

Задание 1. Изобразите графически:

1. Неориентированное и ориентированное ребро;

4. Полный неориентированный граф на трех, четырех и пяти вершинах;

5. Неполный ориентированный граф на пяти вершинах;

7. Неориентированный и ориентированный мультиграф.

Решение:

1) Неориентированное ребро ориентированное ребро

Задание 2. Изобразить графы в программах:

grin_rus, Grafoanalizator1.3.3 rus, windisc ru.

Задание:

Вариант № 1

Задание 1. Выполните задание по образцу.

G ( V , E ) — орграф.

Задание 2. Изобразите графы в соответствующих программах. Полученные графы сохранить в свои папки.

Граф	Программа
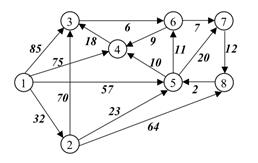	Grafoanalizator1.3.3 rus
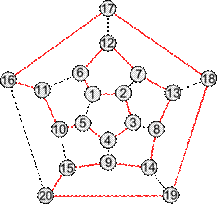	grin_rus
	windisc ru

Вариант № 2

Задание 1. Выполните задание по образцу.

G ( V , E ) — орграф.

Задание 2. Изобразите графы в соответствующих программах. Полученные графы сохранить в свои папки.

Граф	Программа
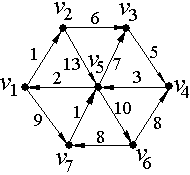	Grafoanalizator1.3.3 rus
	grin_rus
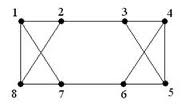	windisc ru

Вариант № 3

Задание 1. Выполните задание по образцу.

G ( V , E ) — орграф.

Задание 2. Изобразите графы в соответствующих программах. Полученные графы сохранить в свои папки.

Граф	Программа
	Grafoanalizator1.3.3 rus
	grin_rus
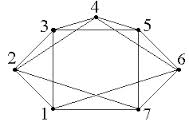	windisc ru

Вариант № 4

Задание 1. Выполните задание по образцу.

G ( V , E ) — орграф.

Задание 2. Изобразите графы в соответствующих программах. Полученные графы сохранить в свои папки.

Граф	Программа
	Grafoanalizator1.3.3 rus
	grin_rus
	windisc ru

Порядок выполнения работы:

1. Изучить инструкцию к практической работе.

2. Выполнить задание.

3. Оформить отчет.

Содержание отчета:

4. Материальное обеспечение.

5. Практическое задание.

Вопросы для самоконтроля:

1.Что называется графом? Ориентированным графом? Приведите примеры.

2.Что такое степень вершины?

3.Перечислите основные понятия, связанные с неориентированными графами.

4.Перечислите основные понятия, связанные с орграфами.

5.В чем состоит аналитический способ задания графа?

6.В чем состоит геометрический способ задания графа?

7.В чем состоит матричный способ задания графа?

8.Что называется маршрутом, циклом и цепью графа?

9.Сформулируйте понятие связности графа. Какой граф называют связным?

10.Какие два графа называются изоморфными?

11.Сформулируйте алгоритм изоморфизма двух графов.

12.Перечислите операции над графами.

Практическая работа № 2,3

Тема: Решение задач по теории графов. Эйлеровы и Гамильтоновы графы.

Цель: изучить алгоритмпоиска эйлерова, гамильтонова цикла (пути) в графе, рассмотреть на конкретных примерах ориентированные и неориентированные графы.

Задачи:

1. Закрепить знания основных понятий теории графов.

2. Приобрести практические умения использования специального программного обеспечения для моделирования.

3. Использовать математический аппарат теории графов

Материальное обеспечение:

Программа анализатор графов: Grafoanalizator1.3.3 rus, практическое задание.

Теоретическая часть:

Эйлеровы графы

К задачам на Эйлеровы графы относятся головоломки, в которых требуется вычертить на плоскости одним росчерком замкнутые кривые, обводя каждый участок в точности один раз. Введём следующие понятия.

Эйлеровым путём в графе называется путь, содержащий все рёбра графа.

Эйлеровым циклом или эйлеровой цепью называется цикл, содержащий все рёбра графа и притом по одному разу.

Граф, обладающий эйлеровым циклом, называется эйлеровым графом.

Замкнутую линию, если её можно начертить, не отрывая карандаша от бумаги, проходя при этом каждый участок в точности один раз, принято называть уникурсальной.

Рисунок графа, обладающий эйлеровым путём или эйлеровым циклом, является уникурсальной линией.

Докажем следующие две теоремы

Теорема 1. Если граф обладает эйлеровым циклом, то он связный и все его вершины четные.

Доказательство. Связность графа следует из определения эйлерова цикла. Эйлеров цикл содержит каждое ребро и притом только один раз, поэтому, сколько раз эйлеров путь приведет конец карандаша в вершину, столько и выведет, причём уже по одному ребру. Следовательно, степень каждой вершины графа должна состоять из двух одинаковых слагаемых: одно – результат подсчета входов в вершину, другое – выходов.

Теорема 2. Если граф связный и все его вершины четные, то он обладает эйлеровым циклом.

Доказательство. Если начать путь из произвольной вершины графа , то найдётся цикл, содержащий все рёбра графа. Пусть — произвольная вершина. Из начнём путь по l по одному из рёбер и продолжим его, проходя каждый раз по новому ребру. Все вершины графа имеют чётные степени, поэтому если l есть «выход» из , то должен быть и «вход» в , также как и для любой вершины другой вершины. И если есть «вход» в вершину, то должен быть и «выход». Так как число ребер конечно, то это путь должен окончиться, причём в вершине . Если путь, замкнувшийся в , проходит через все рёбра графа, то мы получим искомый эйлеров цикл.

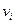
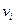
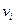
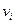
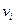
Для построения эйлерова цикла в связном графе со всеми вершинами чётной степени применяется следующий алгоритм:

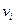
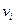
1. Выйти из произвольной вершины . Каждое пройденное ребро зачеркнуть. Если путь замыкается в и проходит через все рёбра графа, то получим искомый эйлеров цикл.

2. Если остались непройденные рёбра, то должна существовать вершина принадлежащая и ребру, не вошедшему в

3. Так как чётная, то число рёбер, которым принадлежит и которые не вошли в путь тоже чётно. Начнём новый путь из и используем только рёбра, не принадлежащие Этот путь кончится в

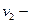
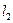
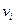
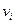
4. Объединим теперь оба цикла: из пройдём по пути к затем по и, вернувшись в пройдём по оставшейся части обратно в .

5. Если снова найдутся рёбра, которые не вошли в путь, то найдём новые циклы. Так как число рёбер и вершин конечно, то процесс закончится.

Таким образом, замкнутую фигуру, в которой все вершины чётные, можно начертить одним росчерком без повторений и начиная с любой точки.

На практике эйлеровым графом может быть план выставки; это позволяет расставить указатели маршрута, чтобы посетитель смог пройти по каждому залу в точности по одному разу.

Гамильтоновы графы

Граф, обладающий гамильтоновым циклом, называется гамильтоновым графом.

Гамильтоновым циклом, или путём в графе, называется цикл, или путь, проходящий через каждую вершину графа в точности по одному разу.

Эйлеровы и гамильтоновы пути сходны по способу задания. Первые содержат все рёбра, и притом по одному разу, вторые – все вершины по одному разу. Но, несмотря на внешнее сходство, задачи их отыскания резко отличаются по степени трудности. Для решения вопроса о существовании эйлерова цикла в графе достаточно выяснить, все ли его вершины чётные.

Критерий же существования гамильтонова цикла на произвольном графе ещё не найден.

Однако есть несколько достаточных условий существования гамильтоновых циклов в графе:

1. Всякий полный граф является гамильтоновым, так как он содержит простой цикл, которому принадлежат все вершины данного графа.

2. Если граф, помимо простого цикла, проходящего через все его вершины, содержит и другие рёбра, то он также является гамильтоновым.

3. Если граф имеет один гамильтонов цикл, то он может иметь и другие гамильтоновы циклы.

Дата добавления: 2019-02-22 ; просмотров: 2937 ; Мы поможем в написании вашей работы!

Источник