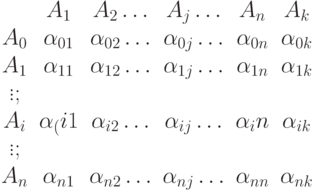Граф схем способ описания алгоритма

10 Графовых алгоритмов

Oct 31, 2020 · 6 min read

Графы превратились в невероятно сильное средство моделирования и получения данных из соцсетей, веб-страниц и ссылок, а также определения местоположения и маршрутов в GPS. Любой набор объектов, которые связаны друг с другом, можно сейчас представить с помощью графа.

В статье опишем 10 основных графовых алгоритмов, которые становятся очень полезными для анализа, а также области их применения.

Начнём с того, что приведём определение графа.

Что такое граф?

Граф состоит из конечного множества вершин (узлов) и набора рёбер, соединяющих эти вершины. Две вершины считаются смежными, если они соединены друг с другом одним и тем же ребром.

Ниже приве д ён ряд базовых понятий, относящихся к графам. Они проиллюстрированы примерами на рисунке 1.

• Порядок: число вершин в графе.
• Размер: число рёбер в графе.
• Степень вершины: число рёбер, инцидентных вершине.
• Изолированная вершина: вершина, которая не связана ни с одной другой вершиной графа.
• Петля: ребро, вершины которого совпадают.
• Ориентированный граф: граф, в котором все рёбра имеют направление, определяющее начальную и конечную вершину.
• Неориентированный граф: граф с рёбрами, которые не имеют направления.
• Взвешенный граф: рёбра такого графа имеют определённый вес.
• Невзвешенный граф: рёбра такого графа не имеют никаких весов.

Источник

Граф-схемы алгоритмов

4. Граф-схемы алгоритмов

ГСА – это ориентированный связный граф, задающий последовательность выполнения операций данного алгоритма и содержащий ряд операторных и условных вершин, а также одну начальную и одну конечную вершины. Операторной называется вершина, – которой сопоставляется одна или несколько микроопераций и отмечается соответствующими управляющими сигналами У, а условной – вершина, которой сопоставляется некоторое логическое условие X.

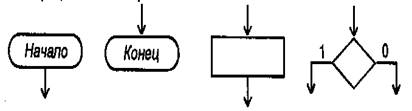
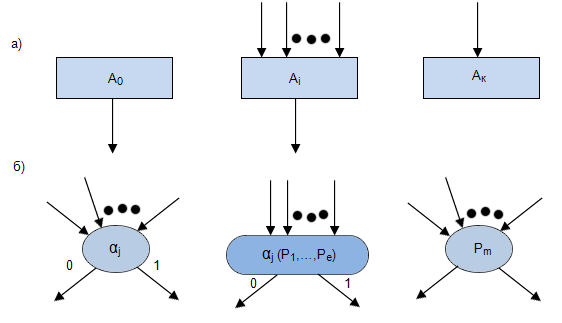
Любая вершина ГСА, кроме вершины «Начало», имеет по одному входу. Вершина «Начало» входов не имеет. Вершина «Начало» и любая операторная вершина имеют по одному выходу. Вершина «Конец» выходов не имеет. Любая условная вершина имеет два выхода, помечаемых символами «Да» и «Нет»: Вместо этих символов могут быть использованы цифры «1» и «О» соответственно. Изображение вершин «Начало», «Конец», операторной вершины и условной вершины ГСА представлено на рис. 2.

Рисунок 2-Графы схемы алгоритмов

ГСА составляют так, чтобы обеспечить выполнение необходимых операций и проверку логических условий в соответствии со словесным описанием алгоритма.

На основании перечня микроопераций и реализующих их функциональных узлов составляется структурная схема ОА. Здесь широкими стрелками показаны шины, по которым передается информация, а тонкими – сигналы у, управляющие работой отдельных узлов или передачей информации по шинам.

ГСА должна удовлетворять следующим условиям:

1. Входы и выходы вершин соединяются друг с другом с помощью направленных всегда от выхода к входу.

2. Каждый выход соединен только с одним входом.

3. Любой вход соединяется, по крайней мере, с одним выходом.

4. Любая вершина ГСА лежит, по крайней мере, на одном пути из вершины «Начало» в вершину «Конец».

5. Один из выходов условной вершины может соединяться с ее входом, что недопустимо для операторной вершины. Такие условные вершины иногда называются возвратными.

6. В каждой условной вершине записывается логическое условие из множества логических условий. Разрешается в различных условных вершинах записывать одинаковые логические условия.

7. В каждой операторной вершине записывается оператор, представляющий собой выходной сигнал или совокупность выходных сигналов управляющего автомата. Разрешается в различных операторных вершинах записывать одинаковые операторы.

5. Содержательные граф-схемы алгоритмов

Обычно при проектировании различных устройств предварительно составляется так называемая содержательная ГСА, в которой внутри условных и операторных вершин записаны логические условия и микрооперации в содержательных терминах.

В качестве примера построим содержательную ГСА устройства, вычисляющего функцию знака числа:

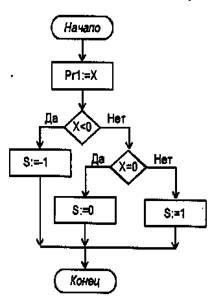
Соответствующая содержательная ГСА представлена на рис. 3.

Рисунок 3. Содержательная ГСА функции определения знака числа

6. Синтез управляющего автомата по граф-схеме алгоритма

Конечный управляющий автомат, реализующий микропрограмму работы дискретного устройства, принято называть микропрограммным автоматом. Как уже отмечалось, микропрограмма отображается с помощью ГСА. Рассмотрим последовательность этапов синтеза управляющего автомата по его ГСА.

1. Запись словесного алгоритма функционирования операционного автомата (выполняемых операций) с учетом структуры операционного автомата.

2. Построение содержательной ГСА функционирования операционного автомата.

3. Построение отмеченной ГСА с учетом типа автомата.

4. Построение графа переходов автомата или таблицы переходов.

5. Проведение структурного синтеза автомата по его графу переходов известными методами, например, с помощью канонического метода структурного синтеза.

Построение отмеченной ГСА производится по содержательной ГСА. Для автоматов Мили и Мура процедура разметки имеет различия.

6.1 Построение отмеченной ГСА автомата Мили

Если необходимо построить микропрограммный автомат Мили, то содержательная ГСА управляющего автомата размечается в соответствии со следующими правилами:

1) символом состояния a₁ отметить вход вершины, следующей за вершиной «Начало», а также вход вершины «Конец»;

2) входы всех вершин, следующих за операторными, должны быть отмечены символами а с последовательными индексами;

3) если выход вершины отмечается, то только одним символом;

4) входы различных вершин, за исключением вершины «Конец», отмечаются различными символами;

5) содержательные термины микроопераций и логических условий. заменяются их условными обозначениями: в каждой операторной вершине последовательно проставляются символы выходных сигналов, если в различных операторных вершинах записаны одинаковые микрооперации, то разрешается их отмечать одинаковыми символами выходных сигналов; если в различных условных вершинах записаны одинаковые логические условия, то разрешается их отмечать одинаковыми символами входных сигналов.

6.2 Построение отмеченной ГСА автомата Мура

Если необходимо построить микропрограммный автомат Мура, то содержательная ГСА управляющего автомата размечается в соответствии со следующими правилами:

1) символом a₁ отмечаются вершины «Начало» и «Конец»;

2) различные операторные вершины отмечаются различными символами;

3) все операторные вершины должны быть отмечены.

4) содержательные термины микроопераций и логических условий. заменяются их условными обозначениями.

Содержательная ГСА (рис. 3.) после разметки по приведенному алгоритму представлена на рис. 5.

После получения отмеченной ГСА строится граф переходов автомата. Он имеет столько различных вершин, сколько различных букв а_i с индексами имеется в отмеченной ГСА. Каждая вершина графа переходов автомата отмечается буквой а с соответствующим индексом.

Между двумя вершинами графа имеется дуга, если на отмеченной ГСА между вершинами с метками a_i и a_k, имеется путь. Над дугой ставится входной сигнал, равный конъюнкции логических условий соответствующего пути в отмеченной ГСА. При этом выполнению логического условия соответствует переменная без отрицания, а невыполнению логического условия – переменная с отрицанием на соответствующей дуге графа переходов автомата.

Если в отмеченной ГСА между упомянутыми вершинами с метками a_i и а_k имеется несколько путей, то в графе переходов автомата на дуге, связывающей а_i и а_k через символ дизъюнкции перечисляются все конъюнкции, соответствующие имеющимся путям.

Если строится граф переходов автомата Мура, то символы микроопераций (выходные сигналы управляющего автомата) записываются около соответствующих его вершин. Для автомата Мили символы микроопераций записываются на соответствующих дугах при конъюнкциях логических условий, описывающих путь через операторную вершину с рассматриваемой микрооперацией.

Если в отмеченной ГСА имеется безусловный переход между операторными вершинами, т.е. путь, не проходящий ни через какие условные вершины, то на графе переходов автомата ему соответствует дуга, которой приписывается входной сигнал «1», показывающий, что данный переход в автомате осуществляется при поступлении очередного синхросигнала.

В дальнейшем синтез проводится с помощью описанного ранее метода структурного синтеза. Подчеркнем, что входными сигналами синтезируемого структурного автомата являются конъюнкции булевых переменных (или дизъюнкции конъюнкций), каждая из которых отображает путь через соответствующие условные вершины отмеченной ГСА, а выходными сигналами – микрооперации, обозначающие либо вершины, либо дуги графа переходов автомата, в зависимости от его типа. Используя канонический метод структурного синтеза, можно построить функциональную схему автомата.

Источник

Способы описания работы дискретных устройств

3.2 Граф-схемы алгоритмов

ГСА находят широкое применение в практике проектирования устройств ЦВМ и, в частности, микропрограммных автоматов в силу их хорошей обозримости, простоты конструкции языка и возможности преобразований и формального перехода к автоматному отображению.

Основными символами, используемыми при записи граф -схем алгоритмов (ГСА), будем считать:

• операторы,
• логические условия,
• стрелки (рис.3.6).

Из всего множества операторов выделяются:

• начальный оператор ,
• конечный оператор ,
• произвольный оператор .

Начальный оператор в дальнейшем (если это особо не оговаривается) будем рассматривать как оператор, символизирующий начало работы алгоритма.

Особенность записи оператора 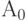в ГСА состоит в том, что в этот оператор не входит ни одной стрелки.

Конечный оператор будем рассматривать как оператор, символизирующий конец работы алгоритма.

Особенность записи оператора и в ГСА состоит в том, что из этого оператора не выходит ни одной стрелки.

Произвольные операторы будем рассматривать как символы, обозначающие определённые действия, акты, связанные с реализацией алгоритма.

Особенность записи операторов 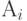состоит в том, что в эти операторы могут входить несколько стрелок, но выходит всегда только одна стрелка.

Под логическим условием будем понимать логическую функцию вида , где элементарные логические условия. Особенность записи логических условий состоит в том, что они могут иметь несколько входящих стрелок и только две выходящие, помеченные символами «О» и «I» в со-ответствии со значением логического условия. В дальнейшем будем допускать также ГСА замену левой части выражения вида его правой частью.

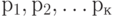
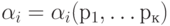
Стрелки обеспечивают упорядочение последовательности выполнения операторов и проверки логических условий, а также их взаимосвязей.

Выполнение алгоритма всегда начинается с оператора 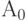и заканчивается оператором .

3.3Формулы переходов

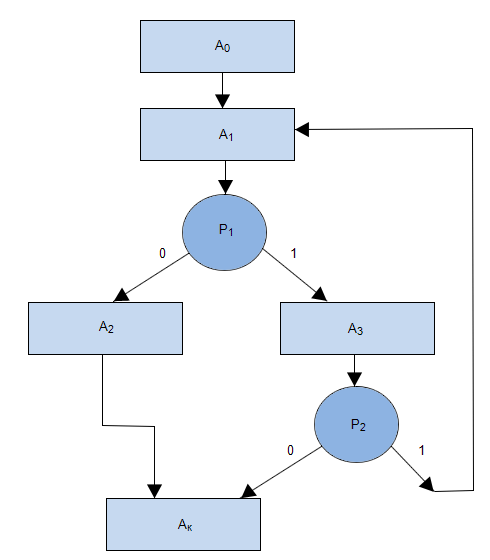
В общем виде для каждой операторной вершины формула перехода записывается так:

причем свойства ортогональности и полноты так же соблюдаются. Кроме того считается, что значения наборов логических условий в процессе выполнения операторов не меняются.

Для МП, представленной на рис.3.7, формулы перехода будут записаны так:

;

;

;

;

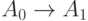
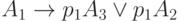
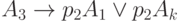
3.4. Матричные схемы алгоритмов

Говорят, что задана матричная схема алгоритма (МСА), если задана матрица вида

где — операторы ,

— начальный и конечный операторы ,

— логические условия, имеющие тот же смысл, что и в ГСА.

Таблица 3.1.

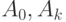
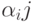
А1	А2	А3	Аk
A0	1
A1	p1	p1
A2	1
A3	p2	p2

В MCA принято рассматривать как такую логическую функцию , что если выполнялся оператор и на образовавшемся наборе значений элементарных логических условий функция получила значение , равное единице, то непосредственно после оператора должен выполняться оператор .

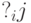
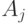
В рис.3.1,а приводится МСА МП, показанной на рис.3.7.

Источник
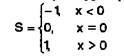