Граф как способ решения задач

Метод графов. Решение задач методом графов. (материалы для занятий математического кружка в 5 классе)
материал по математике (5 класс) на тему

В статье предложена подборка задач, одним из способов решения которых является метод графов. Этот метод позволяет легко и красиво решать задачи типа «Кто есть кто?», весьма интересен и вызывает живой интерес у обучающихся.

Материал может быть использован при проведении занятий математического кружка и развития интереса к математики у обучающихся 5 класса.

Скачать:

Вложение	Размер
metod_grafov._reshenie_zadach_metodom_grafov.doc	65.5 КБ

Предварительный просмотр:

Метод графов. Решение задач методом графов.

(материалы для занятий математического кружка в 5 классе)

Один из способов решения задач типа «Кто есть кто?» — метод графов .
Граф – это несколько точек, часть которых соединены друг с другом отрезками или стрелками (в этом случае граф называется ориентированным).

Другой способ решения таких задач – табличный метод.
Рассмотрим метод графов на примере решения задачи № 1 из предложенных ниже задач.

Задача №1: Любители мультфильмов:

Жила-была одна дружная семья: мама, папа и сын. Они все любили делать вместе. Но вот мультфильмы любили разные: «Ну, погоди!», «Покемоны», «Том и Джерри». Определите, какой мультфильм любит каждый из них, если мама, папа и любитель мультфильма «Покемоны» никогда не унывают, а папа и любитель мультфильма «Том и Джерри» делают зарядку по утрам?

Рассмотрим метод графов на примере решения задачи:

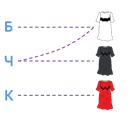
Рассмотрим множество людей: мама, папа, сын и множество мультфильмов «Ну, погоди!», «Покемоны», «Том и Джерри». Обозначим элементы этих двух множеств точками:

Если точке из одного множества соответствует точка другого множества, будем соединять эти точки сплошной линией, если не соответствует – то штриховой.
Заметим, что по условию задачи у человека только один любимый мультфильм.
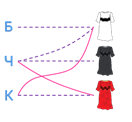
Учитывая данные задачи, получаем следующую схему:

Из условия задачи следует, что нужно найти единственно возможное соответствие между элементами двух множеств.
Правило: если какая-то точка оказывается соединенной с двумя точками другого множества штриховыми линиями, то с третьей точкой она должна быть соединена сплошной.
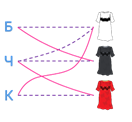
Поэтому граф на рисунке будет выглядеть следующим образом:

Теперь мы установили, что папа любит мультфильм «Ну, погоди!», сын – «Покемоны». В обеих множествах остается только по одной точке, следовательно мама любит мультфильм «Том и Джерри». Задача решена.
Таким же способом можно находить соответствие между тремя множествами. Тогда при решении мы можем получить треугольники трех видов:
а) все стороны являются сплошными отрезками (решение задачи);
б) одна сторона – сплошной отрезок, а две другие – штриховые;
в) все стороны – штриховые отрезки.
Таким образом, нельзя получить треугольник, у которого бы две стороны были сплошными отрезками, а третья – штриховой отрезок.

Задача №2: Любители музыки:

В клубе «Отдых» познакомились 3 любителя клубной музыки видов техно, хаус, рейв. Один говорит: «Вы какую музыку больше любите? Я техно люблю!». Другой ответил, что любит хаус, а третий сказал, что не любит ни техно, ни хаус, но зато обожает рейв. Интересно то, что все они были в банданах и рубашках черного, белого и желтого цветов, но цвет банданы и рубашки совпадал только у любителя техно. А у любителя хаус ни рубашка, ни бандана не были белыми. А любитель рейв был в желтой рубашке. Определите цвет рубашек и бандан каждого из любителей клубной музыки.

Задача №3: Три поросёнка:

Жили-были на свете три поросёнка, три брата: Ниф-Ниф, Наф-Наф, Нуф-Нуф. Построили они три домика: соломенный, деревянный и кирпичный. Все три брата выращивали возле своих домиков цветы: розы, ромашки и тюльпаны. Известно, что Ниф-Ниф живет не в соломенном домике, а Наф-Наф – не в деревянном; возле соломенного домика растут не розы, а тот, у кого деревянный домик, выращивает ромашки. У Наф-Наф аллергия на тюльпаны, поэтому он не выращивает их. Узнайте, кто в каком домике живет и какие цветы выращивает.

Задача №4: Друзья

Встретились три друга — Белов, Серов и Чернов. Чернов сказал другу, одетому в серый костюм: «Интересно, что на одном из нас белый костюм, на другом — серый и на третьем — черный, но на каждом костюм цвета, не соответствующего фамилии». Какой цвет костюма у каждого из друзей?

Задача №5: Подруги:

Когда три подруги — Надя, Валя и Маша — вышли гулять, на них были белое, красное и синее платья. Туфли их были тех же трех цветов, но только у Нади цвета туфель и платья совпадали. При этом у Вали ни платье, ни туфли не были синими, а Маша была в красных туфлях. Определите цвет платьев и туфель каждой из подруг.

Задача №6: Друзья

Встретились трое друзей: Белов, Рыжов и Чернов. Брюнет сказал Белову: «Любопытно, что ни у кого из нас цвет волос не соответствует фамилии, да и ты не брюнет».

Какой цвет волос у каждого из друзей?

Задача №7: Подруги:

Три ученицы – Валя, Галя и Катя – пришли в театр в платьях разного цвета: одна – в белом, другая – в сером, а третья – в черном. Катя была не в черном, Валя не в черном и не в сером. Угадай, в какое платье каждая из них была одета.

В семье четверо детей. Им 5, 8, 13 и 15 лет, а зовут их Аня, Юра, Света и Лена. Сколько лет каждому из них, если одна девочка ходит в детский сад, Аня старше, чем Юра, а сумма лет Ани и Светы делится на три?

Катя, Боря, Витя и Юра заняли первые четыре места на олимпиаде. Катя не заняла ни первое, ни последнее место, Боря занял второе место, Витя оказался в числе первых трех призеров. Какое место на олимпиаде занял Юра?

Три друга Алеша, Боря и Витя едут после школы домой на различном транспорте: автобусе, троллейбусе, трамвае. Однажды после уроков Алеша пошел проводить своего друга домой до остановки автобуса. Когда мимо них проходил троллейбус, третий друг крикнул из окна: «Боря, ты забыл в школе тетрадку». Кто на чем ездит домой?

Клоуны Бам, Бим, Бом вышли на арену в красной, синей и зеленой рубашках. Их туфли тоже были этих трех цветов. Туфли и рубашка Бима были одного цвета. на Боме не было ничего красного. Туфли Бама были синие, а рубашка нет. Какого цвета были туфли и рубашка у Бома и Бима?

Задача № 12 Мушкетёры:

Атос, Портос, Арамис и Д’Артаньян – четыре талантливых молодых мушкетёра. Один из них лучше всех сражается на шпагах, другой не имеет равных в рукопашном бою, третий лучше всех танцует на балах, четвертый без промаха стреляет с пистолетов. О них известно следующее:
• Атос и Арамис наблюдали на балу за их другом – прекрасным танцором.
• Портос и лучший стрелок вчера с восхищением следили за боем рукопашника.
• Стрелок хочет пригласить в гости Атоса.
• Портос был очень большой комплекции, поэтому танцы были не его стихией.
Кто чем занимается?

1. Папа любит мультфильм «Ну, погоди!», сын – «Покемоны», мама любит мультфильм «Том и Джерри».
2. У любителя «техно» рубашка и бандана белого цвета; у любителя «хаус» черная рубашка и желтая бандана; у любителя «рейв» желтая рубашка и черная бандана.
3. Наф-Наф живет в кирпичном домике и выращивает розы; Ниф-Ниф живет в деревянном домике и выращивает ромашки; Нуф-Нуф живет в соломенном домике и выращивает тюльпаны.
4. Чернов в белом костюме, Белов — в сером, Серов — в черном.
5. У Нади туфли и платье синего цвета; у Вали туфли белые, платье красное; у Маши туфли красные, платье белое.
6. Белов – рыжий, Чернов – блондин, Рыжоа – брюнет
7. Валя – в белом, Галя – в черном, Катя – в сером
8. Анне – 13 лет, Юре – 8 лет, Свете – 5 лет, лене – 15 лет.
9. Последнее (четвертое)
10. Леша ездит на трамвае, Боря — на автобусе, Витя – на троллейбусе.
11. У Бома синяя рубашка и зеленые туфли, у Бама зеленая рубашка и синие туфли.
12. Арамис – стрелок; Д’Артаньян – танцор; Портос – шпажист; Атос – рукопашник.

Источник

Решение простых комбинаторных задач с помощью графов

Понятие графа

Кроме таблиц, удобным инструментом для перебора и подсчёта различных комбинаций является граф.

Граф – это абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер, то есть соединений между парами вершин.

Граф из 6 вершин и 7 ребёр.

Сколько различных трёхзначных чисел можно написать с помощью цифр 0 и 1?

Получаем 4 числа: 100,101,110 и 111

Полный граф в комбинаторике

Полный граф – это граф со всеми возможными ребрами.

С помощью полного графа удобно решать задачи полного перебора про «всех со всеми».

5 школьных команд по волейболу сыграли серию игр. Каждая команда провела с другими командами по одному матчу. Сколько всего матчей было сыграно?

Изобразим полный граф с 5-ю вершинами и посчитаем количество ребёр.

N = 10. Значит, было сыграно 10 матчей.

Граф-дерево

Дерево – это граф без циклов, у которого между парами вершин имеется только одно ребро.

Граф-дерево с 9 узлами и 8 ребрами.

Из каждого узла выходит не более 2 ребер.

Такое дерево называют бинарным.

С помощью дерева удобно составлять упорядоченные комбинации элементов.

На столе стоит три стакана сока – апельсиновый, виноградный и яблочный. Можно взять только два стакана. Сколько есть возможных вариантов и каких?

По правилу произведения число возможных вариантов: $3 \cdot 2 = 6$. Поскольку, порядок выбора неважен, остаётся $\frac<6> <2>= 3$ варианта. Построим граф:

3 варианта: 1) апельсиновый + яблочный, 2)апельсиновый + виноградный, 3) виноградный + яблочный.

Примеры

Пример 1. Вася, Петя, Коля и Толя хотят быть дежурными в столовой. Но можно выбрать только троих. Сколько вариантов выбора есть?

Построим полный граф.

Каждая тройка ребят соответствует треугольнику в этом графе.

Например, Вася образует три треугольника с оставшимися тремя ребятами:

$ \frac<3\cdot 2> <2>= 3$ — ВПК, ВТК и ВТП

Без Васи есть только один треугольник – ПКТ

Общее количество треугольников 3+1=4

Ответ: 4 варианта

Пример 2. Под рукой есть 6 видов овощей (капуста, морковь, лук, помидоры, огурцы и перец). Для салата нужно 3 вида овощей. Сколько всего различных салатов можно приготовить?

Построим полный граф.

Каждые три овоща на полном графе образуют треугольник.

Например, капуста образует треугольники с оставшимися 5 овощами. Таких треугольников $ \frac<5\cdot 4> <2>= 10$, где деление на 2 учитывает повторение ребра в каждой паре («лук-огурец» = «огурец-лук» и т.д.).

Количество треугольников, в которые не входит капуста: $ \frac<4\cdot 3> <2>= 6$

Количество треугольников, в которые не входят капуста и морковь: $ \frac<3\cdot 2> <2>= 3$

Количество треугольников, в которые не входят капуста, морковь и перец: $ \frac<2\cdot 1> <2>= 1$

Итого 10+6+3+1 = 20 различных треугольников.

Ответ: 20 салатов

Примечание: по расчетной формуле $C_6^3 = \frac<6\cdot 5 \cdot 4> <1\cdot 2 \cdot 3>= 20$ — ответ правильный.

Пример 3*. Сколько существует способов занять 1,2 и 3 места на чемпионате, в котором участвуют 11 команд? Решите задачу с помощью полного графа.

Если построить полный граф с 11-ю вершинами, каждая тройка команд в нём образует треугольник.

По аналогии с примерами 1 и 2, общее количество треугольников:

Так, как порядок мест важен, в каждом треугольнике $– 3\cdot2 = 6$ вариантов распределения медалей.

По правилу произведения: $6\cdot165 = 990$ — общее количество способов.

Ответ: 990 вариантов

Примечание: по расчетной формуле $A_3^ <11>= 11\cdot10\cdot9 = 990 $ — ответ правильный.

Пример 4. В столовой есть на выбор

• два первых блюда: щи (Щ) и борщ (Б)
• три вторых блюда: мясо (М), рыба (Р), блинчики с творогом (Т)
• два напитка: компот (К) и сок (С)

Сколько вариантов обедов можно составить из этих блюд и каких?

По правилу произведения общее количество вариантов обедов: $2\cdot3\cdot2 = 12$

Построим дерево для перечисления вариантов:

Источник

Решение задач с помощью графов

Урок 6. Математика и игры 3–4 классы

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Решение задач с помощью графов»

Прежде чем приступить к решению задач, стоит сказать, что графы, о которых пойдёт речь, к аристократам былых времён никакого отношения не имеют. У наших графов в корне есть греческое слово «графо», что значит «пишу». Этот же корень («граф») встречается, например, в словах «график, «биография», «орфография» и некоторых других.

Давайте выясним понятие графа на примере решения задачи.

В первенстве класса по настольному теннису шесть участников: Андрей, Саша, Вова, Оля, Дима и Лена. Каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Сашей, Олей и Леной; Саша, как уже говорилось, с Андреем и ещё с Олей; Вова – с Олей, Димой и Леной. Сколько игр уже проведено и сколько ещё осталось?

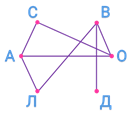
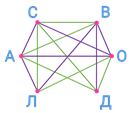
Итак, изобразим данные этой задачи в виде схемы. Участников первенства обозначим точками, расположив их по окружности: Андрей – А, Саша – ЭС, Вова – ВЭ, Оля – О, Дима – ДЭ, Лена – ЭЛЬ.

Если двое участников уже сыграли между собой, то будем соединять, обозначающие их точки отрезками. В условии задачи сказано, что Андрей сыграл с Сашей, Олей и Леной.

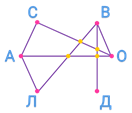
Мы уже видим, что Саша сыграл с Андреем, а ещё он сыграл с Олей.

Вова сыграл с Олей, Димой и Леной.

Получившаяся схема называется графом. Точки А, С, В, О, ДЭ, Л называются вершинами графа. Отрезки, которые соединяют вершины графа, называются рёбрами графа. Каждое ребро соединяет две вершины графа.

При этом обратите внимание, что точки, в которых пересекаются рёбра графа, не являются его вершинами.

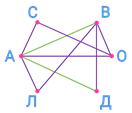
У графа 7 рёбер. Это означает, что к настоящему моменту было проведено 7 игр.

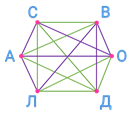
Чтобы найти количество игр, которые осталось провести, продолжим построение этого графа так, чтобы из каждой точки были проведены рёбра ко всем остальным точкам. Но для того, чтобы потом легче было подсчитать количество добавленных рёбер, рисовать их будем другим цветом.

Итак, известно, что Андрей сыграл с Сашей, Олей и Леной. А значит, он не играл с Вовой и Димой.

Также известно, что Саша сыграл с Андреем и с Олей, а значит, он не сыграл с Вовой, Димой и Леной.

Вова сыграл с Олей, Димой и Леной. Получается, что он не сыграл с Андреем и Сашей. Но соответствующие отрезки уже проведены.

Оля сыграла с Андреем и Сашей, а также с Вовой. Это значит, что она ещё не сыграла с Димой и Леной.

Дима сыграл только с Вовой. Ему предстоит сыграть с Олей, Сашей и Андреем, но эти отрезки мы уже провели. Осталось провести отрезок от Димы к Лене.

Лена сыграла с Андреем и Вовой. Ей предстоит сыграть с Димой, Олей и Сашей, но эти отрезки мы уже провели. Больше ничего добавлять не надо.

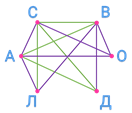
Мы добавили 8 рёбер. Это значит, что осталось провести ещё 8 игр. Получается, что ответ на вопрос задачи будет таким: проведено 7 игр, осталось провести 8 игр.

Отметим, что граф для одной и той же задачи можно нарисовать разными способами. И наоборот, для разных задач можно нарисовать одинаковые по виду графы.

Также отметим, что иногда рёбра удобнее изображать не отрезками, а «дугами».

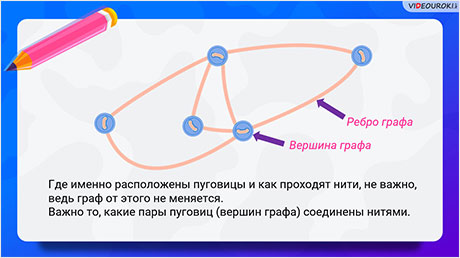
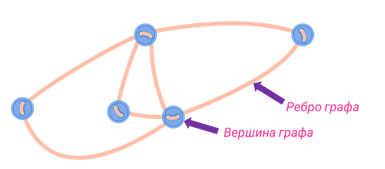
Граф можно представить как набор пуговиц, некоторые из которых соединены нитями. Пуговицы – это вершины графа, нити – его рёбра.

При этом, где именно расположены пуговицы, и как проходят нити не важно, ведь граф от этого не меняется. Важно то, какие пары пуговиц (то есть вершин графа) соединены нитями.

Но при решении задач, подобных приведённой, удобнее всё-таки располагать вершины по окружности. Тогда при проведении рёбер рисунок получается не таким запутанным.

Если из вершины графа выходит чётное количество рёбер, то её называют чётной. А если из вершины графа выходит нечётное количество рёбер, то её называют нечётной.

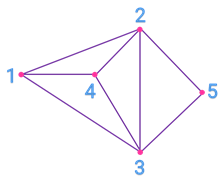
Посмотрите на такой граф.

У него вершины 1 и 4 являются нечётными, так как из них выходят по 3 ребра.

А вот вершины 2, 3 и 5 являются чётными, так как из вершины под номером 2 выходят 4 ребра, из вершины под номером 3 тоже выходят 4 ребра, а из вершины под номером 5 выходят 2 ребра.

Решим следующую задачу. Встретились три подруги: Белова, Чернова и Краснова. На одной из них было чёрное платье, на другой – красное, на третьей – белое. Девочка в белом платье говорит Черновой: «Нам надо поменяться платьями, а то у всех троих цвет платьев не соответствует фамилиям». Кто в какое платье был одет?

На одном из наших занятий было предложено решить эту задачу с помощью таблицы. Давайте решим её с помощью рисунка.

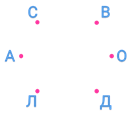
Обозначим фамилии девочек буквами. Пусть напротив буквы Б будет белое платье, напротив буквы Ч – чёрное, напротив буквы К – красное.

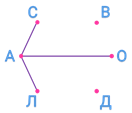
Соединим пунктирной линией букву Б и белое платье. Это означает, что Белова не в белом платье. Также соединим пунктирными линиями букву Ч и чёрное платье, букву К и красное платье. Это означает, что Чернова не в чёрном платье, а Краснова не в красном платье.

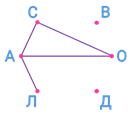
В условии задачи говорится, что девочка в белом платье говорит Черновой: «Нам надо поменяться платьями, а то у всех троих цвет платьев не соответствует фамилиям». Получается, что Чернова одета не в белое платье. Поэтому соединим букву Ч с белым платьем пунктирной линией.

Теперь, внимательно посмотрев на рисунок, становится понятно, что ни Белова, ни Чернова не одеты в белое платье. Значит, в белое платье одета Краснова. Поэтому соединим букву К и белое платье сплошной линией.

Так как на Чернова была одета не в белое платье, а также на ней не могло быть чёрного платья, то, следовательно, она была в красном платье. Соединим сплошной линией букву Ч и красное платье.

Мы выяснили, что Краснова была в белом платье, а Чернова была в красном. А значит, Белова была в чёрном платье. Соединим букву Б и чёрное платье сплошной линией.

Ответ на вопрос задачи будет таким: Белова была одета в чёрное платье, Чернова – в красное платье, Краснова – в белое платье.

И решим ещё одну задачу. Из города А в город Б ведут 3 дороги, а из города Б в город Б – 4 дороги. Сколькими способами можно проехать из города А в город В, если по пути надо обязательно заехать в город Б?

Решение. Отметим точками города А, Б и В. В условии задачи сказано, что из города А в город Б ведут 3 дороги. Также сказано, что из города Б в город В ведут 4 дороги.

Возьмём одну дорогу, которая ведёт из города А в город Б. Её можно продолжить до города В четырьмя различными способами.

Если взять вторую дорогу, которая ведёт из города А в город Б, то и её можно продолжить до города В четырьмя различными способами.

То же самое можно сказать и про третью дорогу, ведущую из города А в город Б, то есть её также можно продолжить до города В четырьмя способами.

Получается, что по какой бы из трёх дорог из города А в город Б мы не поехали, продолжить дорогу в город В можно четырьмя способами.

Таким образом, из города А в город В через город Б можно проехать 3 умножить на 4, то есть 12 способами.

Источник