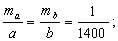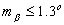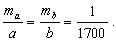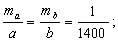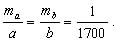Геометрическое нивелирование. Способы геометрического нивелирования. Порядок работы на станции. Контроль измерений.
Геометрическое нивелирование выполняется горизонтальным лучом визирования. Геометрическое нивелирование, при котором превышение между точками получают как разность отсчетов по рейкам при горизонтальном положении визирной оси нивелира. Этот метод является наиболее простым и точным, но позволяет с одной постановки прибора получить превышение не более длины рейки.
Геометрическое нивелирование выполняется горизонтальным лучом визирования
1)Нивелирование из середины HA=HB+h
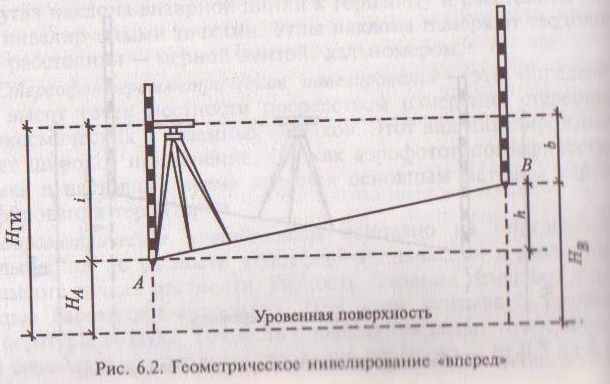
2)Нивелирование вперёд. Целесообразно применять в том случае, когда на небольшом участке необходимо определить превышение или высоты нескольких точек. Удобно высоты точек определять через горизонт прибора. h=i-bHГП=HA+i, HB=HГП-b.
2. Способы геометрического нивелирования.
Геометрическое нивелирование основано на применении нивелира, который обеспечивает горизонтальное положение линии визирования. Геометрическое нивелирование может быть выполнено также с помощью теодолита-тахеометра.

Классификация нивелиров и нивелирных реек.
В зависимости от устройств, применяемых для приведения визирной оси трубы в горизонтальное положение, нивелиры изготавливают двух видов — с цилиндрическим уровнем на зрительной трубе и с компенсатором углов наклона, т.е. без цилиндрического уровня.
Нивелиры бывают трех классов точности:
а) Н-05, Н-1, Н-2 — высокоточные для нивелирования I и II классов;
б) Н-3 — точные для нивелирования III и IV классов;
в) Н-10 — технические для топографических съемок и других видов инженерных работ.
Число в названии нивелира означает среднюю квадратическую погрешность в мм нивелирования на 1 км двойного хода. Для обозначения нивелиров с компенсатором к цифре добавляется буква -К, а для нивелиров с горизонтальным лимбом — буква Л, например Н-10КЛ.
Устройство нивелира с цилиндрическим уровнем. Поверки, юстировки.
1)Окуляр 2)Зрительная труба 3)Коробка цилиндрического уровня 4)Барабан кремальеры 5)Объектив 6)Закрепительный винт 7)Наводящий винт 8)Трегер 9)Подъемные винты 10)Пружинная пластина 11)Исправительный винт круглого уровня 12)Элевационный винт 13)Круглый уровень (для предварительной установки прибора)
Поверки:1)Ось круглого уровня должна быть параллельна основной оси 2)Вертикальный штрих сетки нитей должен быть параллелен основной оси 3)Ось цилиндрического уровня должна быть параллельна визирной оси.
Устройство нивелира с компенсатором. Поверки, юстировки.
Наводящий винт; Корпус нивелира; Объектив; Барабан кремальеры; Окуляр; Зрительная труба; Круглый уровень (для предварительной установки прибора); Зеркало; Подъемные винты; Фокусирующая линза; Подвижная призма компенсатора; Неподвижная призма компенсатора; Сетка нитей; Демпфер.
Поверки: 1) Ось круглого уровня должна быть параллельна основной оси 2)Вертикальный штрих сетки нитей должен быть параллелен основной оси 3)Визирный луч должен быть горизонтален в пределах угла компенсации.
Точность геометрического нивелирования. Источники ошибок измерения превышений
И способы их ослабления.
Источники ошибок при геометрическом нивелировании.
Ошибка установки визирной линии трубы в горизонтальное положение по уровню; при t = 25″ она достигает 3″ — 4″. Для расстояния 100 м это приводит к ошибке отсчета по рейке 2 мм.
Ошибка отсчета из-за ограниченной разрешающей способности трубы нивелира; при увеличении V = 25x эта ошибка достигает 1.2 мм на 100 м расстояния.
Нарушение главного условия нивелира; при нивелировании строго из середины эта ошибка исключается.
Наклон рейки. Для уменьшения влияния наклона рейки ее рекомендуется слегка покачивать вперед-назад около вертикального положения; при отсчетах меньше 1000 мм рейку качать нельзя. При покачивании рейки отсчеты по ней изменяются; наименьший отсчет является правильным.
Ошибка нанесения делений на рейке. Общая ошибка отсчета по шашечной рейке нивелиром Н-3 оценивается в 4 мм на 100 м расстояния.
Источник
Геометрический способ
Определение площади участков местности
Существует три способа определения площади участков: геометрический, аналитический и механический. На местности применяют два первых способа, на картах и планах — все три способа.
Геометрический способ — это вычисление площади геометрических фигур по длинам сторон и углам между ними, значения которых можно получить только из измерений.
Сначала рассмотрим простейшую фигуру — треугольник.
Формулы для вычисления площади треугольника известны:
P = 0.5 * a * b * Sin(C) (6.2)

в этих формулах:
a, b, c — длины сторон треугольника,
A, B, C — углы при вершинах против соответствующих сторон,
h — высота, проведенная из вершины A на сторону a,
p — полупериметр, p=0.5*(a + b + c).
Для решения любого n-угольника нужно знать (2*n — 3) его элементов, причем количество известных углов не должно быть больше (n-1), так как один угол всегда может быть вычислен, если остальные углы известны, на основании формулы:
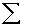
При расчете ошибки определения площади следует учитывать ошибки всех (2n-3) измеряемых элементов.
В треугольнике нужно знать (измерить) три элемента. Формула (6.1) содержит всего два элемента; это значит, что прямой угол между основанием и высотой нужно отдельно обеспечить с необходимой точностью, что равнозначно одному измерению.
Примем относительную ошибку площади mp/P = 1/1000, тогда для применения формулы (6.1) на основании принципа равных влияний необходимо выполнить условия:
где ma,mb,β — ср.кв. ошибки сторон a, b и прямого угла между основанием и высотой.
Для формулы (6.2) на основании принципа равных влияний можно написать:
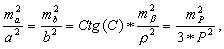
Считая попрежнему mp/P=1/1000, получим:
Если в треугольнике измерять три стороны с относительной ошибкой mS/S и для вычисления площади применять формулу (6.3), то для равностороннего треугольника получим:
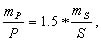
Таким образом, вариант с измерением трех сторон треугольника оказывается самым эффективным, так как в нем не требуется измерять углы.
Четырехугольник, как геометрическая фигура, может быть параллелограммом, ромбом, трапецией, прямоугольником, квадратом; но как участок местности его следует считать фигурой произвольной формы, так как обеспечение геометрических свойств той или иной фигуры на местности требует дополнительных измерений.
В четырехугольнике (n=4) нужно измерить пять элементов: три угла и две стороны или два угла и три стороны или один угол и четыре стороны или четыре стороны и одну диагональ. Последний вариант является наиболее предпочтительным, так как, во-первых, в нем не нужно измерять углы, и, во-вторых, согласно формуле:
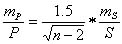
относительная ошибка площади примерно равна относительной ошибке измерения сторон. Во всех остальных вариантах при оценке точности площади нужно учитывать как ошибки измерения сторон, так и ошибки измерения углов.
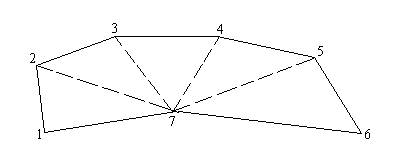
Применение геометрического способа на местности требует разбиения участка на простые геометрические фигуры, что возможно лишь при наличии видимости внутри участка (рис.6.1.)
При определении площади участков на топографических планах и картах стороны и высоты треугольников, стороны и диагонали четырехугольников нужно измерять с помощью поперечного масштаба.
Для определения площади на карте или плане геометрическим способом часто используют палетку — лист прозрачной бумаги, на котором нанесена сетка квадратов или параллельных линий. Палетку с квадратами накладывают на участок и подсчитывают, сколько квадратов содержится в данном участке; неполные квадраты считают отдельно, переводя затем их сумму в полные квадраты. Площадь участка вычисляют по формуле:
где a — длина стороны квадрата,
M — знаменатель масштаба карты,
n — количество квадратов на участке.
Применение палеток с параллельными линиями описано в [23].
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Геометрический способ
Существует три способа определения площади участков: геометрический, аналитический и механический. На местности применяют два первых способа, на картах и планах — все три способа.
Геометрический способ — это вычисление площади геометрических фигур по длинам сторон и углам между ними, значения которых можно получить только из измерений.
Сначала рассмотрим простейшую фигуру — треугольник.
Формулы для вычисления площади треугольника известны:
P = 0.5 * a * b * Sin(C) (6.2)
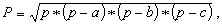
в этих формулах:
a, b, c — длины сторон треугольника,
A, B, C — углы при вершинах против соответствующих сторон,
h — высота, проведенная из вершины A на сторону a,
p — полупериметр, p=0.5*(a + b + c).
Для решения любого n-угольника нужно знать (2*n — 3) его элементов, причем количество известных углов не должно быть больше (n-1), так как один угол всегда может быть вычислен, если остальные углы известны, на основании формулы:
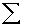
При расчете ошибки определения площади следует учитывать ошибки всех (2n-3) измеряемых элементов.
В треугольнике нужно знать (измерить) три элемента. Формула (6.1) содержит всего два элемента; это значит, что прямой угол между основанием и высотой нужно отдельно обеспечить с необходимой точностью, что равнозначно одному измерению.
Примем относительную ошибку площади mp/P = 1/1000, тогда для применения формулы (6.1) на основании принципа равных влияний необходимо выполнить условия:
где ma,mb,β — ср.кв. ошибки сторон a, b и прямого угла между основанием и высотой.
Для формулы (6.2) на основании принципа равных влияний можно написать:
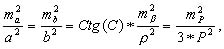
Считая попрежнему mp/P=1/1000, получим:
где a — длина стороны квадрата,
M — знаменатель масштаба карты,
n — количество квадратов на участке.
Применение палеток с параллельными линиями описано в [23].
Источник
Способы геометрического нивелирования
Лекция VII
Нивелирование.
Нивелирование – вид геодезических работ, в результате которых определяют разности высот (превышения)точек земной поверхности, а также высоты этих точек над принятой отсчетной поверхностью.
Различают следующие виды нивелирования:
1) геометрическое нивелирование заключается в непосредственном определении разности высот двух точек с помощью горизонтального визирного луча.
2) тригонометрическое нивелирование заключается в определении превышений между точками по измеренному между ними расстоянию и углу наклона. Вычисление превышений ведут по формулам тригонометрии.
3) Физическое делится на три вида: а)барометрическое, в основу которого положена зависимость между величиной атмосферного давления на точке местности и ее высотой; б) гидростатическое, основанное на свойстве свободной поверхности жидкости в сообщающихся сосудах всегда находиться на одинаковом уровне независимо от превышения точек, на которых установлены эти сосуды (рис. 7-7); в) радиолокационное, основанное на использовании отражения электромагнитных волн.
4) Механическое нивелирование производят с помощью специальных приборов, устанавливаемых на велосипедных рамках, автомобилях и т.д. (рис. 7-6). При движении такого прибора автоматически регистрируются пройденные им расстояния, высоты точек и вычерчивается профиль пройденного пути.
5) Стереографическое нивелирование основано наопределении превышений по паре фотоснимков одной и той же местности.
Наиболее часто в инженерной практике применяется геометрическое нивелирование.
Способы геометрического нивелирования
Геометрическое нивелирование производят специальными приборами – нивелирами (рис. 7-8). Различают два способа геометрического нивелирования: «из середины» и «вперед».
Нивелирование из середины. Для определения превышения т.В над т.А устанавливают в них вертикально рейки R1 и R2, а между ними по возможности на одинаковом расстоянии от реек нивелир (рис. 7-3(а)). Последовательно визируя на рейки средней горизонтальной нитью зрительной трубы берут отсчеты: по задней рейке aи по передней рейке b. Тогда:
h = a – b, (1)
т.е. превышение равно отсчету по задней рейке минус отсчет по передней рейке. При a > b превышение положительно, при a


алгебраическая сумма всех превышений равна превышению между конечными точками, т.е.:

Отметки связующих точек вычисляют последовательно по формуле (2). Если требуется отметка только конечной точки хода, то ее определяют по формуле:
Нкон = Ннач + 
Отметки промежуточных точек вычисляют через горизонт инструмента.
Устройство нивелира дается на лабораторном занятии.
Источник