Гистограмма это способ представления

Гистограмма

Большая советская энциклопедия. — М.: Советская энциклопедия . 1969—1978 .

Полезное

Смотреть что такое «Гистограмма» в других словарях:

гистограмма — гистограмма … Орфографический словарь-справочник

ГИСТОГРАММА — (histogram) Диаграмма, представляющая распределение переменной величины, в том случае если имеется информация об отдельных ее значениях. Площади на диаграмме пропорциональны числу соответствующих наблюдений в каждом интервале, например ежегодных… … Экономический словарь

Гистограмма — (histogram) График распределения частот, который строится при помощи прямоугольников, чья площадь пропорциональна частоте нахождения данной величины в интервале, на котором построен данный прямоугольник. Бизнес. Толковый словарь. М.: ИНФРА М ,… … Словарь бизнес-терминов

ГИСТОГРАММА — (от греч. histos здесь столб и . грамма) (столбчатая диаграмма), один из видов графического изображения статистических распределений какой либо величины по количественному признаку. Гистограмма представляет собой совокупность смежных… … Большой Энциклопедический словарь

Гистограмма — фигура, получающаяся на плоскости, где введены декартовы координаты и по оси абсцисс отложены группированные наблюдения, а по оси ординат число соответствующих наблюдений. Верхняя часть контура Г. есть статистический аналог плотности… … Геологическая энциклопедия

Гистограмма — в техническом анализе интервальный график, на котором каждому временному интервалу ставится в соответствие отрезок прямой (палочка), начало и конец которого есть высшая и низшая цены периода. При этом цены открытия и закрытия отмечаются на… … Финансовый словарь

гистограмма — – это способ графического представления распределения числовых (непрерывных) данных, часто используемый в разведочном анализе данных для иллюстрации основных характеристик распределения. Диапазон возможных значений переменной делится на отрезки,… … Словарь социологической статистики

гистограмма — один из способов графического представления количественных данных в виде прямоугольных «столбиков», примыкающих друг к другу и соответственных частоте каждого класса данных. Словарь практического психолога. М.: АСТ, Харвест. С. Ю. Головин. 1998.… … Большая психологическая энциклопедия

гистограмма — График, состоящий из вертикальных или горизонтальных полос, высота или ширина которых пропорциональны значениям данных. [http://www.morepc.ru/dict/] гистограмма столбиковая диаграмма [Лугинский Я. Н. и др. Англо русский словарь по электротехнике… … Справочник технического переводчика

ГИСТОГРАММА — ГИСТОГРАММА, столбчатовидная диаграмма, столбцы которой представляют собой частоту (в абсолютных величинах или процент от общего), с которой определенные величины (или диапазоны величин) встречаются в пределах некоторого набора данных. см. также… … Научно-технический энциклопедический словарь

гистограмма — сущ., кол во синонимов: 1 • диаграмма (9) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Источник

ГИСТОГРАММА

Гистограмма, это способ представления статистических данных в графическом виде – в виде столбчатой диаграммы. Она отображает распределение отдельных измерений параметров изделия или процесса. Иногда ее называют частотным распределением, так как гистограмма показывает частоту появления измеренных значений параметров объекта.

Высота каждого столбца указывает на частоту появления значений параметров в выбранном диапазоне, а количество столбцов – на число выбранных диапазонов.

Важное преимущество гистограммы заключается в том, что она позволяет наглядно представить тенденции изменения измеряемых параметров качества объекта и зрительно оценить закон их распределения. Кроме того, гистограмма дает возможность быстро определить центр, разброс и форму распределения случайной величины. Строится гистограмма, как правило, для интервального изменения значений измеряемого параметра.

Порядок построения гистограммы следующий:

1. Собираются статистические данные – результаты измерений параметра объекта. Для того, чтобы гистограмма позволяла оценить вид распределения случайной величины предпочтительно иметь не менее тридцати результатов измерений.

2. Выявляется наибольшее и наименьшее значение показателя среди полученных результатов измерений.

3. Определяется ширина диапазона значений показателя – из наибольшего значения показателя вычитается наименьшее значение.

4. Выбирается надлежащее число интервалов в пределах которых необходимо сгруппировать результаты измерений.

5. Устанавливаются границы интервалов. Границы интервалов необходимо установить так, чтобы значения данных не попадали ни на одну из границ интервала. Например, если были выбраны интервалы с границами от 0,5 до 5,5 от 5,5 до 10,5 и т.д. то значение данных 5,5 будет попадать как в первый, так и во второй интервал. Чтобы избежать этой проблемы можно изменить интервалы от 0,51 до 5,50 от 5,51 до 10,50 и так далее, таким образом ни одно значение данных не попадет на границу интервала.

6. Подсчитывается число попаданий значений результатов измерений в каждый из интервалов.

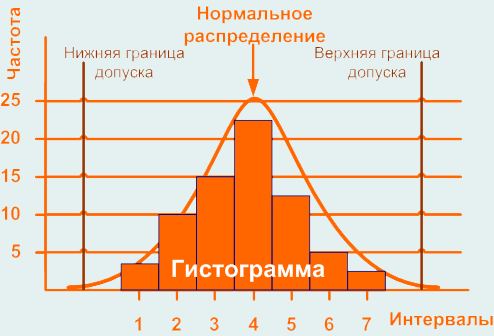
7. Строится гистограмма – на оси абсцисс (горизонтальной оси) отмечаются интервалы, а на оси ординат (вертикальной оси) отмечается частота попаданий результатов измерений в каждый интервал. Интервалы можно устанавливать в натуральных единицах (если позволяет масштаб), т.е. в тех единицах, в которых проводились измерения, либо каждому интервалу можно присвоить порядковый номер и отмечать на оси абсцисс номера интервалов. В результате получается столбчатая диаграмма, представленная на рисунке ниже.

Если на контролируемый параметр существует поле допуска, то гистограмма может содержать верхнюю и нижнюю границы поля допуска. Это позволяет увидеть в какую сторону и как смещается значение контролируемого показателя относительно поля допуска. Границы наносятся по оси абсцисс.

Гистограмма, представленная на рисунке выше имеет форму нормального распределения, что говорит о стабильности процесса, но часто бывает, что форма распределения отклоняется от нормального. Это свидетельствует о нарушениях в процессе и необходимости применения управляющих воздействий. Некоторые, часто встречающие отклонения и их причины представлены ниже.

Гистограмма смещена влево (асимметрия влево):

Может вызываться смещением процесса к верхней границе допуска, либо из множества измерений отсортированы результаты, которые выпадают за пределы верхней границы допуска, либо природа процесса физически запрещает любые измерения больше чем максимальные значения допуска.

Гистограмма смещена вправо (асимметрия вправо):

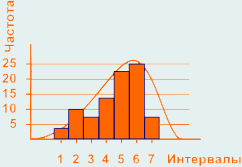
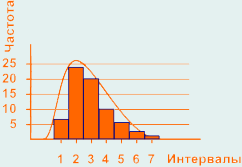
Может вызываться смещением процесса к нижней границе допуска, либо из множества измерений отсортированы результаты, которые выпадают за пределы нижней границы допуска, либо природа процесса физически запрещает любые измерения меньше чем минимальные значения допуска.

Бимодальность:

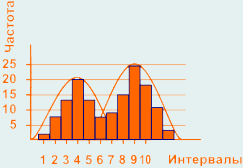
Гистограмма отображает два совмещенных процесса. Такая ситуация может произойти если результаты измерений получены от двух разных устройств, двух операторов, контролеров, разных измерительных инструментов, или с разных точек измерения.

Гистограмма усечена:

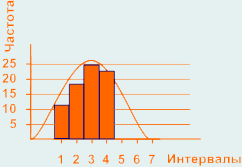
Распределение не является нормальным т.к. нет постепенного снижения частоты результатов измерений от центра к границам допуска. Такой вид гистограммы возникает если процесс не способен удовлетворять спецификациям и часть измерений отсортирована с двух сторон при приближении к границам допуска, либо потеряны чересчур малые значения результатов измерений.

Гистограмма не имеет центра:

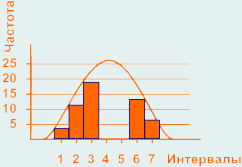
Центр распределения был отсортирован из набора данных результатов измерений. Такая ситуация может возникнуть из-за недостаточных требований в инженерной спецификации.

Гистограмма содержит выступы на границах:

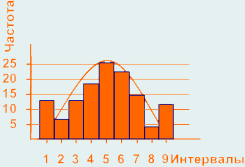
Часть измерений на удаленных от центра сторонах распределения была изменена, чтобы привести характеристики процесса в соответствие с установленным полем допуска или измерения, выходящие за пределы поля допуска были записаны как входящие в поле допуска.

По результатам тестирования по математике учащихся 7-го класса получены данные о доступности заданий теста (отношение числа учащихся, правильно выполнивших задания, к числу тестировавшихся учащихся), предствленные ниже, в таблице.
Тест содержал 25 заданий. Построить гистограмму.

Доступность задания x, %	25-35	35-45	45-55	55-65	65-75	75-85	85-95
Количество задач n

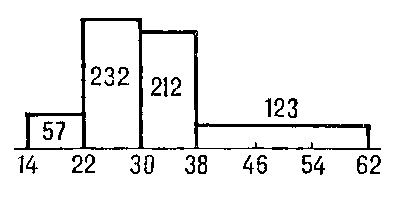
Откладываем на оси абсцисс 7 отрезков длиной 10. На них, как на основаниях, строим прямоугольники, высоты которых соответственно равны 1, 1, 5, 7, 7, 3, 1. Полученная ступенчатая фигура и является искомой гистограммой.

Источник

Гистограмма это способ представления

Войти через uID

Гистограмма – это один из тех немногих способов графического представления данных, доступность и легкость восприятия которого не вызывает сомнения. Она прекрасно подходит для описания больших массивов данных, равно как и для характеристики небольшого числового ряда.

Гистограммы без преувеличения являются одним из наиболее важных инструментов анализа данных в проектах шести сигм. Представление результатов наблюдений с их помощью позволяет исследователю оценить ряд статистических показателей, сделать выводы о функции распределения и определить возможные отклонения, а также сравнить два набора данных (в частности, результаты до и после произведенных действий или внедрения проекта). Во всем этом и множестве других полезных свойствах гистограмм попытаемся разобраться в этой статье.

Информации собрано немало, поэтому для удобства навигации вся статья поделена на разделы. Если вы ищете что-то конкретное, то можно перейти непосредственно к интересующей части по ссылке. Ну а если такой информации не нашлось, обязательно оставьте отзыв в комментариях под публикацией.

Содержание:

Что такое гистограмма?

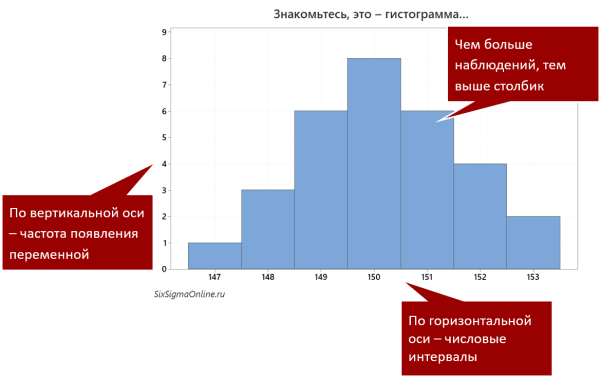
Гистограммой называют двухмерный график, по горизонтальной оси которого откладываются переменные или числовые интервалы, а по вертикальной – частота появления переменной (в заданном интервале).

Чаще всего гистограмма состоит из прямоугольников с шириной, равной величине интервала, и площадью, пропорциональной соответствующей частоте возникновения переменной. Доля всех значений в определенном интервале гистограммы равна его площади (вся площадь гистограммы принимается равной единице, или 100%). Площадь интервала, соответственно, определяет вероятность того, что следующее наблюдение попадет в заданный диапазон результатов. Таким образом, самый высокий столбик гистограммы отвечает интервалу наиболее вероятных результатов.

Другими словами, площадь прямоугольника соответствует количеству значений, которые попадают в определенный интервал: чем больше значений, тем больше площадь – при равных значениях интервалов больший столбик соответствует большему количеству значений.

Отличие от других типов диаграмм и графиков

Забегая наперед, скажу, что гистограмма может принимать самые причудливые формы. Да и для построения этого графика могут применять не только прямоугольники – столбцы, но и кривые, точки, линии… Тем не менее, гистограмма – это также довольно специфический график, и путать его с другими типами диаграммами весьма нерационально.

Чаще всего гистограмму путают со следующими графиками:

• Столбчатая и/или линейчатая диаграмма (Bar Chart).
• Точечная диаграмма (Dotplot).
• Диаграмма “лист и стебель” (Stem-and-Leaf).
• Диаграмма распределения вероятностей (Probability Distribution Plot).
• Диаграмма Парето (Pareto Chart).

Рассмотрим все по порядку.

Отличие гистограммы от столбчатой и/или линейчатой диаграммы

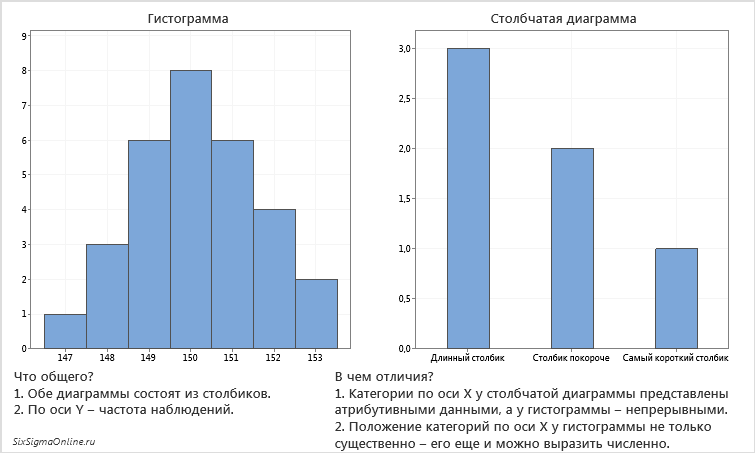
Гистограмма состоит из столбцов, поэтому неудивительно, что ее легко спутать с другой диаграммой, также состоящей из столбцов – столбчатой. Или линейчатой, если говорить о линейках/полосках вместо столбцов. Однако столбчатая и линейчатая диаграммы зачастую отражают количество наблюдений в атрибутивных (или дискретных) категориях, тогда, как у гистограммы по оси Х – непрерывные данные 1 :

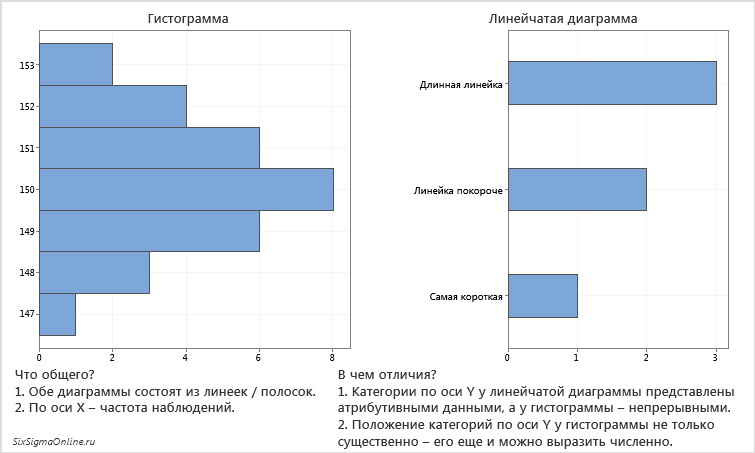
Если диаграммы выше развернуть на 90°, то общие и отличные черты останутся без изменений:

Отдельным пунктом следует выделить диаграмму временного ряда, на которой отложены столбцы вместо точек или линий. У этой диаграммы, как и у гистограммы, по оси X отложены непрерывные данные – дата и/или время. Однако в отличие от гистограммы диаграмма временного ряда показывает наблюдения, упорядоченные во времени, а не распределение значений.

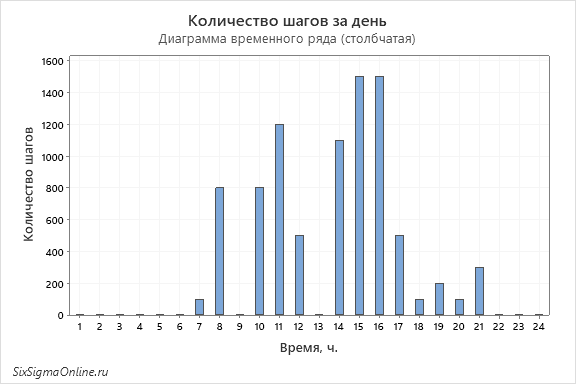
Давайте покажу на примере: сейчас многие носят смарт-часы, которые умеют считать шаги. Допустим, вот так может выглядеть диаграмма временного ряда, если ее сделать столбчатой:

По оси X у нас время в часах, по оси Y – количество шагов в час. Мы видим на диаграмме несколько часов, соответствующих отдыху. В эти часы количество шагов равно 0. Также мы видим несколько часов с большим количеством шагов. К примеру, в период с 14:00 до 16:00 зафиксировано более 1000 шагов в час. Глядя на диаграмму, мы можем сделать вывод о наиболее интенсивных периодах дня и времени отдыха.

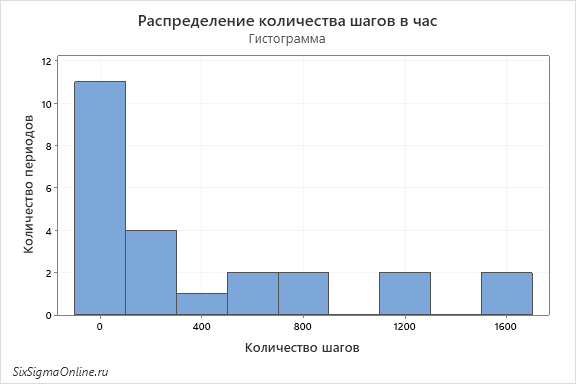
Теперь давайте возьмем те же данные и построим гистограмму:

Это совсем другой график, не правда ли? Из него мы не сможем сделать вывод о том, когда в сутках у нас более активный период, а когда менее. Но мы можем наблюдать некое подобие экспоненциального распределения и утверждать только то, что в сутках мы чаще спим, чем ходим по 1600 шагов в час.

Больше о диаграммах временных рядов вы можете узнать из публикации Анализ временных рядов (Time Series Analysis).

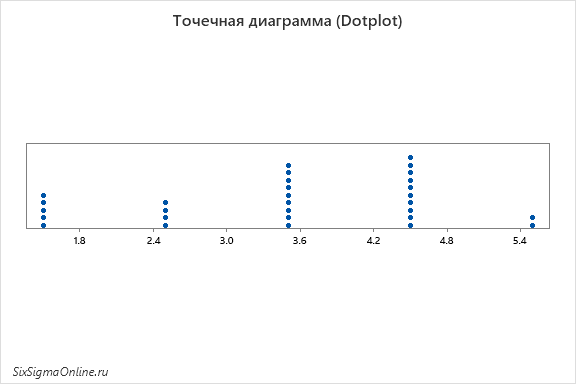
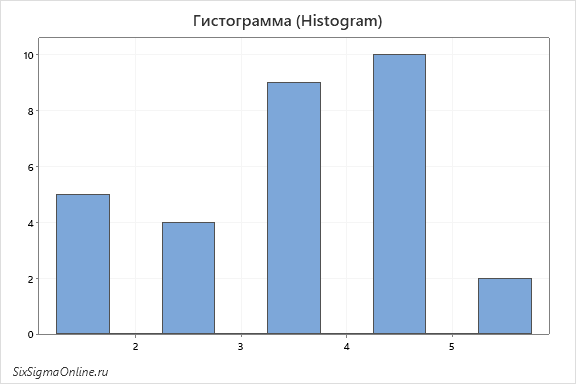
Отличие гистограммы от точечной диаграммы (Dotplot)

И гистограммы, и точечные диаграммы отражают распределение переменной – с тем лишь отличием, что гистограммы чаще всего делают это с помощью столбцов, а точечные диаграммы – (только не удивляйтесь) с помощью точек.

Точечные диаграммы дают нам немного больше представления об индивидуальных наблюдениях, так как отражают каждое из них. Гистограммы, в отличие от них, объединяют наблюдения, которые попадают в один интервал, под одним столбцом. Это преимущество, однако, теряется с увеличением количества наблюдений, так как с увеличением количества единичных наблюдений близкие значения также группируют в точки.

Еще с помощью точечных диаграмм легче заметить “гранулы” – одинаковые значения:

Но чтобы добиться такого же от гистограммы, нужно либо поэкспериментировать с количеством интервалов, либо чтобы “гранулы” наблюдений находились действительно далеко друг от друга:

Больше о точечной диаграмме вы можете узнать из публикации DotPlot в деталях.

Отличие гистограммы от диаграммы “лист и стебель” (Stem-and-Leaf)

Диаграмма “лист и стебель” (Stem-and-Leaf) – это такой себе предшественник гистограммы. Этому графику посвящен отдельный пост на нашем сайте – Что за странный график из листьев и стеблей?, – поэтому вдаваться в детали и описывать его мы не будем. Вместо этого еще раз подчеркнем общие и различные свойства.

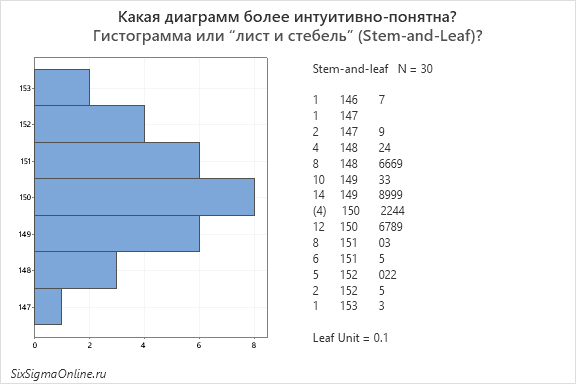
Диаграммы внешне выглядят по-разному, но отражают практически ту же информацию. “Лист и стебель” вполне подойдет для небольшого массива данных, и когда у вас нет под рукой программного обеспечения для построения гистограммы. Вот срочно вам понадобилось на производстве понять распределение наблюдений, а в кармане лишь карандаш и салфетка – рисуйте Stem-and-Leaf.

Гистограмма лучше справится с большим массивом данных и не потребует от вас округления наблюдений, так как недостаток низкого разрешения оставила своему предшественнику. Поэтому если есть возможность построить гистограмму, то выбор очевиден. Кроме того, гистограмма явно нагляднее, чем “лист и стебель”. Да что тут говорить, вы и сами все видите:

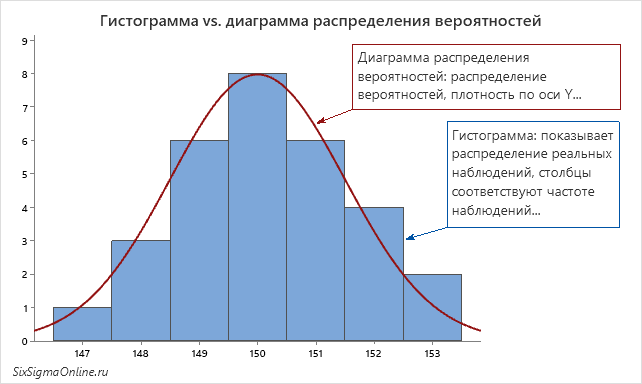
Отличие гистограммы от диаграмм распределения вероятностей (Probability Distribution Plot)

Оба графика – и гистограмма, и диаграмма распределения вероятностей – отражают распределение, только в первом случае это – распределение реальных наблюдений, а во втором – вероятностей, теоретической величины. Как следствие, гистограммы чаще всего покрыты ступенчатыми выступами, соответствующими некоему ограниченному количеству информации о распределении переменной, которое мы обладаем. Диаграмма распределения вероятностей чаще всего отображает плавную линию, соответствующую бесконечному количеству наблюдений:

Есть еще масса мелких отличий – как то: частота наблюдений по оси Y у гистограмм или плотность у диаграмм распределения вероятностей, – но они все являются лишь следствием вышеуказанных особенностей обоих графиков. Кроме того, диаграмма распределения вероятностей может применяться для решения совершенно других задач, нежели гистограмма. Подробнее в статье Диаграмма распределения вероятностей (Probability Distribution Plot).

Отличие гистограммы от диаграммы Парето (Pareto Chart)

Мне не доводилось сталкиваться со случаями, когда гистограмму не могли отличить от диаграммы Парето, но я довольно часто слышу, что диаграмма Парето состоит из гистограммы и некоторых дополнительных элементов. Это не верно. На диаграмме Парето столбцами отражены количества наблюдений в дискретных категориях, при этом колонки ранжированы по убыванию. Ее можно назвать столбчатой диаграммой, но никак не гистограммой.

Диаграмме Парето посвящена не одна публикация на нашем сайте. Попробуйте поиск по соответствующему тегу, чтобы узнать больше.

Если вы сталкивались с заблуждениями относительно гистограммы и других типов диаграмм, которые я не описал выше, буду благодарен за дополнение к статье.

Как построить гистограмму вручную?

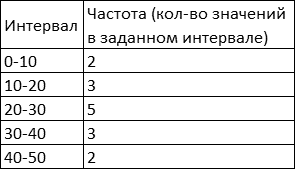
Несмотря на то, что гистограммы легче всего построить, используя программное обеспечение, попробуем сделать это своими собственными силами. Возьмем ряд наблюдений:

3, 5, 11, 12, 19, 22, 23, 25, 27, 29, 35, 36, 37, 45, 49

Сама по себе эта строчка несёт мало информации, но если поделить ее на удобные интервалы, то легко можно сгруппировать все данные и представить в виде следующей таблицы:

Гистограмма, построенная на данных таблицы, будет выглядеть следующим образом:

По оси Y в данном случае отложено количество наблюдений, попадающих в соответствующий диапазон на оси X.

Выбор интервалов (Binning)

Насколько удобным можно назвать выбранный выше интервал? По каким критериям определить, правильно ли он подобран? И как выбор интервала может повлиять на интерпретацию гистограммы? Все это рассмотрим ниже.

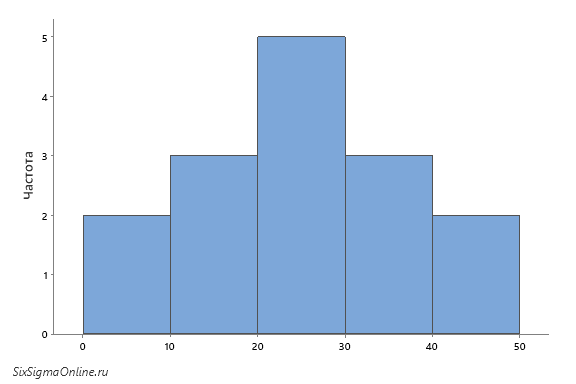
Предположим, вместо пяти отрезков по 10 единиц мы поделим весь диапазон на десять отрезков по 5 – интервалы станут в два раза короче. В таком случае гистограмма примет следующий вид:

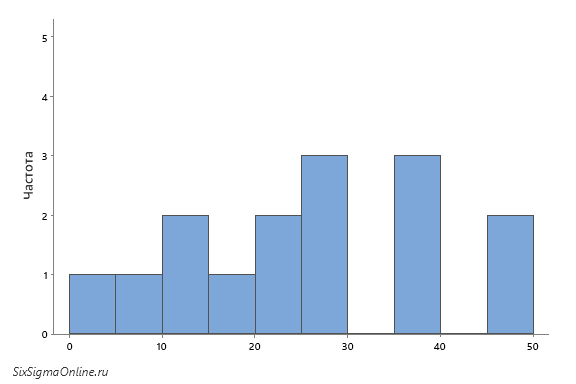
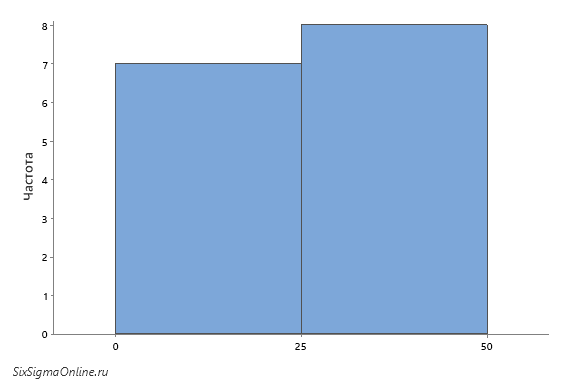
…или всего на 2 интервала – от 0 до 25 и от 25 до 50:

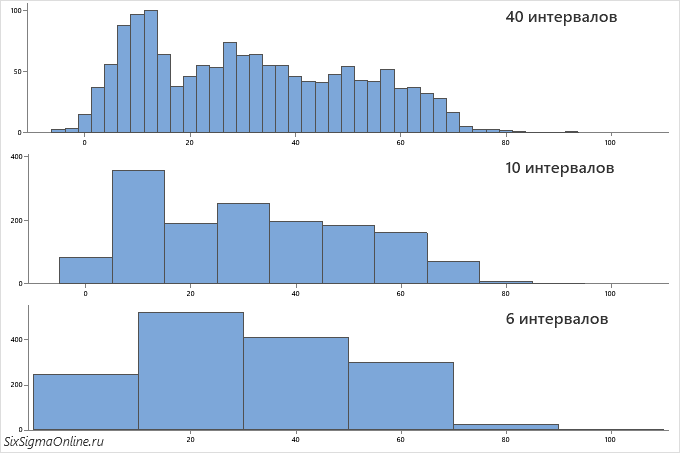
Становится понятно, что один и тот же набор данных может выглядеть совсем по-разному, будучи представленным в виде гистограммы. Определение величины интервала (длинны отрезка по оси X) играет ключевую роль как для визуализации данных, так и для корректности отображаемой информации. При этом подбор диапазонов может не только выявить скрытую информацию о наблюдаемой величине (характеристике процесса), но и сыграть злую шутку, скрыв важную информацию или натолкнув на ложное предположение.

Пример ниже отчетливо иллюстрирует, как распределение наблюдаемой величины, содержащее три моды – пика, – может быть “удачно” замаскировано изменением величины интервалов:

Как же выбрать верный интервал?

К сожалению, для выбора интервалов нет единого верного подхода. Вместо этого есть несколько рекомендаций. К примеру, одна из наиболее общих рекомендаций советует нам разделить весь диапазон наблюдений на 5-30 интервалов. Согласитесь, смысл в этом есть, однако мы уже видели, к чему приводит изменение количества интервалов, а подбирать вручную одну из 25 возможностей – не самая легкая задача. Тем более, что для большого количества данных может понадобиться и больше интервалов.

Еще одна рекомендация говорит, что мы должны поделить весь диапазон так, чтобы в каждый интервал попадало не менее 5-10 наблюдений. Опять же, что делать, когда данных много? И что делать, если в данных есть прореха: например, в один из интервалов не попадет ни одно значение, хотя в интервалах по соседству их будет предостаточно? Разумеется, и в этом случае придется перебрать несколько вариантов, прежде чем мы найдем верный.

Существуют также различные формулы, которые через степени, корни и логарифмы помогут вам найти то самое правильное количество интервалов. Какая формула дает верный результат? При каком расчете от вас не ускользнут нужные детали на графике? Или в каждом случае перебирать все варианты?

Рекомендаций и вариантов расчета гораздо больше, чем нам хотелось бы потратить времени на построение одного графика. Поэтому, к сожалению, вынужден констатировать тот факт, что на практике все либо полагаются на программное обеспечение, либо на собственную “чуйку”, перебирая несколько вариантов вручную и обосновывая это разумными соображениями.

В первом случае, при использовании специализированного ПО, есть хотя бы надежда, что в нем заложен некий алгоритм выбора оптимального количества интервалов. Во втором – при ручном подборе количества интервалов – я не стану утверждать, что опыт не может подсказать, как подобрать верное количество интервалов. Лишь замечу, что от вас все еще может что-то ускользнуть. Как минимум ваше время. Но если вы все же решили заняться подбором количества интервалов вручную и посмотреть, как от этого меняется внешний вид гистограммы, ниже я расскажу вам, как это сделать быстрее всего.

На мой взгляд, первый способ более прагматичен. Строить графики с помощью ПО быстрее и комфортнее, чем в ручном режиме. Коррекция со стороны исследователя иногда необходима, но не обязательна. Нужно позволить программе делать свою работу, а исследователю свою: вместо того, чтобы корпеть над одним графиком, не забывайте:

• Гистограмма – это всего лишь один из возможных методов графического анализа данных. Не ограничивайте себя им в поисках гипотез.
• Гистограмма – это всего лишь графический метод анализа данных, и любой сделанный на его основе вывод требует статистического подтверждения гипотезы.

1. Не смотря на простоту построения и анализа, особенности настройки гистограмм требуют от исследователя значительного опыта и пристального внимания.
2. Выбор интервалов группировки данных определяет информативность и корректность представленных данных. Неправильный подбор может привести к ложному выводу о функции распределения наблюдаемой величины.
3. Избежать этого можно, используя дополнительные методы графического анализа, а также подтверждение гипотез статистическими расчетами.
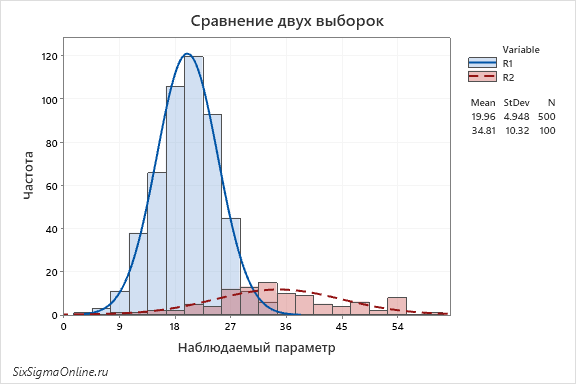
4. Ручная настройка интервалов гистограмм все же нужна в некоторых случаях. Например, при сравнении разных по величине и размаху выборок:

Как построить гистограмму в пакете “101 инструмент вашего проекта шести сигм”?

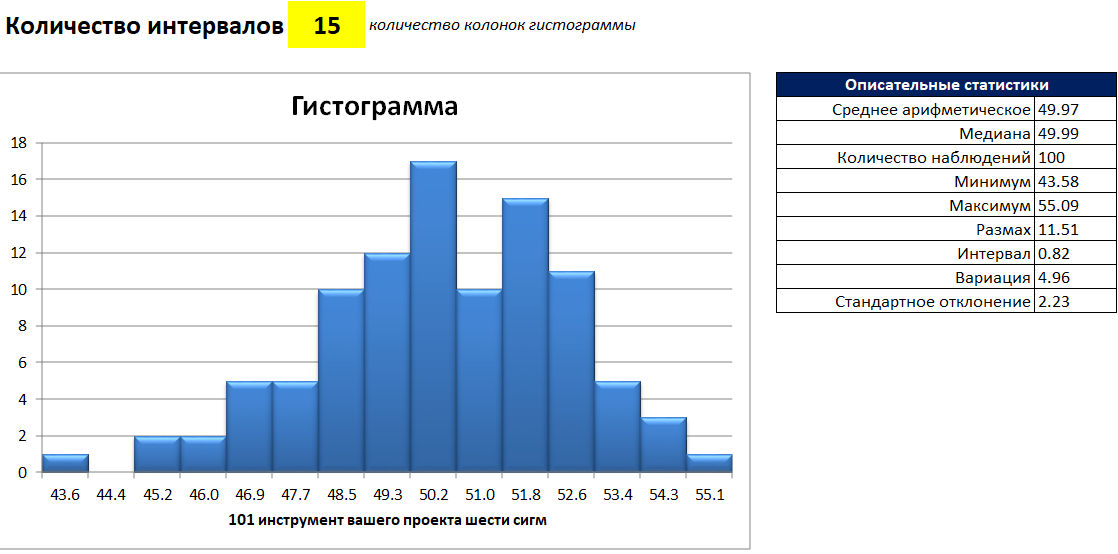
Для построения гистограмм в пакете “101 инструмент вашего проекта шести сигм” откройте папку Measure и выберите инструмент №33 – Histogram. Вам потребуется внести все наблюдения в колонку “B”, и как только это будет сделано, ваша гистограмма готова:

Также обратите внимание на опцию выбора количества интервалов непосредственно над диаграммой. Помните, выше я обещал показать, как сделать ручной подбор наиболее быстрым? Так вот это и есть тот способ. Просто меняйте значение в желтой ячейке от 5 до 30 и следите за тем, как меняется ваша гистограмма.

Как построить гистограмму в Minitab?

Большинство пакетов статистической обработки данных, и Minitab тому не исключение, содержат встроенную функцию и алгоритм построения графиков. С их помощью вся процедура превращения числового ряда в гистограмму сводится к нескольким кликам мышью. С другой стороны, упрощение процесса создания диаграмм – не главное достоинство специализированной программы. Что еще может предложить нам программная среда? Рассмотрим ниже.

Для того, чтобы построить гистограмму, программе необходимы данные – результаты наблюдений, желательно выстроенные в столбик с заголовком-названием. В противном случае построенный график будет иметь название, например, “Hystogram of С1” (где С1 – столбик, в котором размещены данные). Согласитесь, не очень-то информативно. К тому же, если построение гистограммы является частью проекта, то с его расширением разобраться, какая именно гистограмма представляет нужные нам результаты, будет всё труднее.

Как внести данные на рабочий лист программы, читайте в заметке “Заносим” данные: 4 способа. В этой публикации особенности внесения данных упущены – будем считать, что данные уже заданы, и перейдем непосредственно к процессу построения гистограммы.

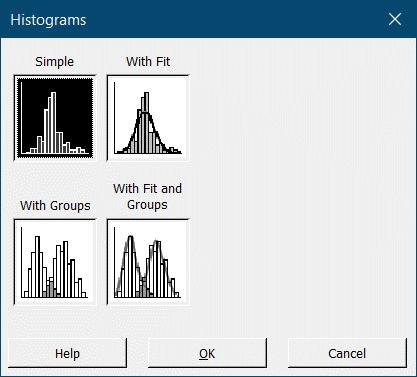
Чтобы построить гистограмму, в меню Graph выберите пункт Histogram. Эта команда откроет окно, которое предложит нам выбрать одну из четырех возможностей:

• Simple – обычная гистограмма.
• With Fit – обычная гистограмма с линией распределения вероятностей (по умолчанию программа наложит линию нормального распределения).
• With Groups – гистограмма различных групп данных.
• With Fit and Groups – гистограмма различных групп данных с наложенной кривой распределения.

Выглядит следующим образом:

Выделенная по умолчанию иконка – Simple или обычная гистограмма – позволит построить простейшую гистограмму. Нажимаем OK, чтобы перейти в следующее меню:

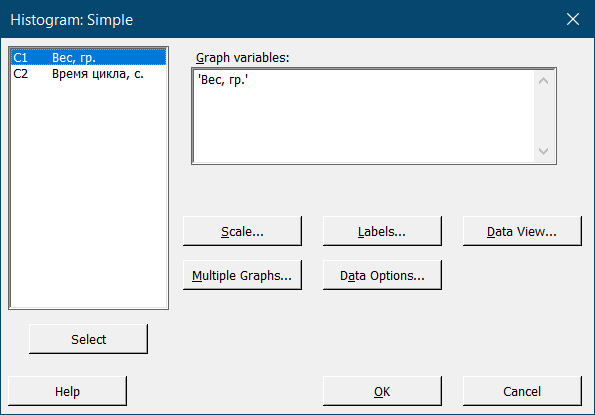
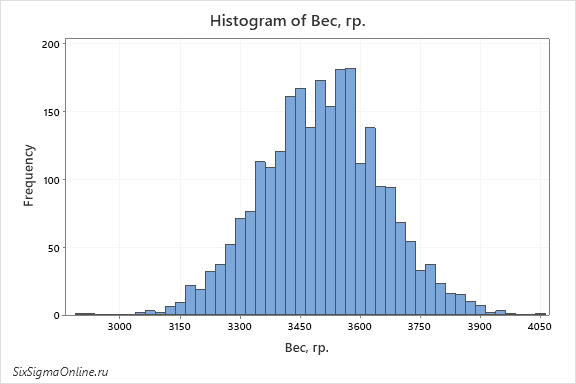
В поле Graph variables можно указать один или несколько столбцов с данными сразу. Для этого нужно дважды кликнуть на нужный столбик в поле слева или выбрать его одним кликом мыши и нажать Select. Как только название столбика появится в поле Graph variables, мы знаем, что нужные данные были заданы. Теперь, чтобы построить гистограмму, достаточно нажать OK:

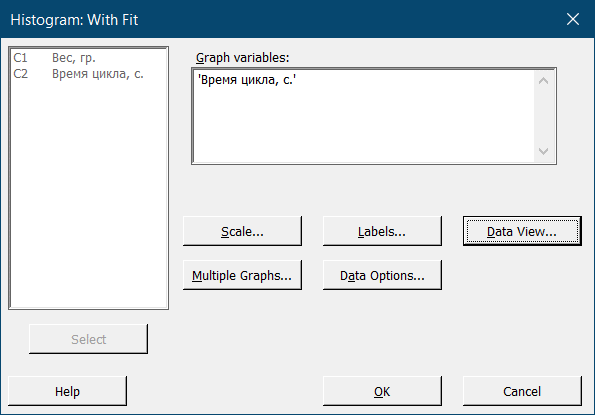
При выборе гистограммы с наложением кривой распределения вероятностей – With Fit – получим гистограмму, на которую будет наложена (по умолчанию) кривая нормального распределения. Если нам известно, что закон распределения отличается от нормального, то в окне настройки гистограммы можем задать функцию, с помощью которой следует аппроксимировать результаты наблюдений. Для этого в окне настроек выберите опцию Data View:

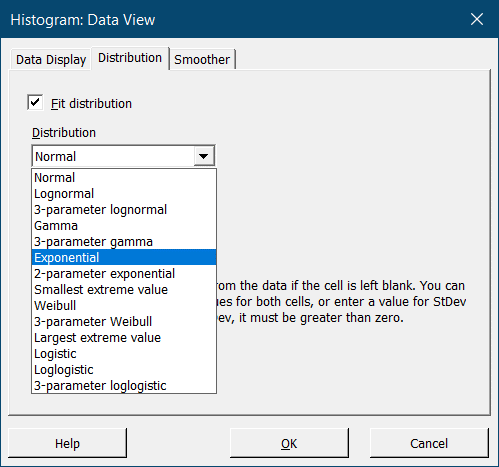
В закладке Distribution следующего меню установите флажок напротив Fit Distribution и выберите необходимый вид распределения в появившемся списке:

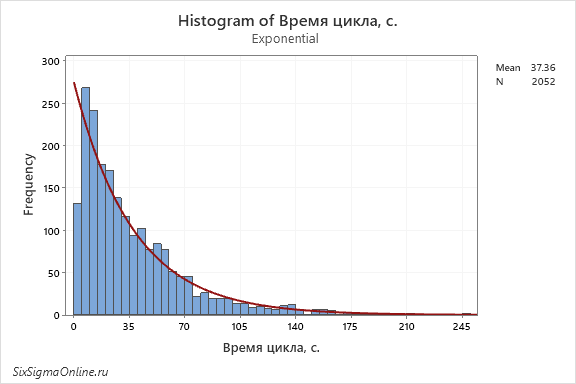
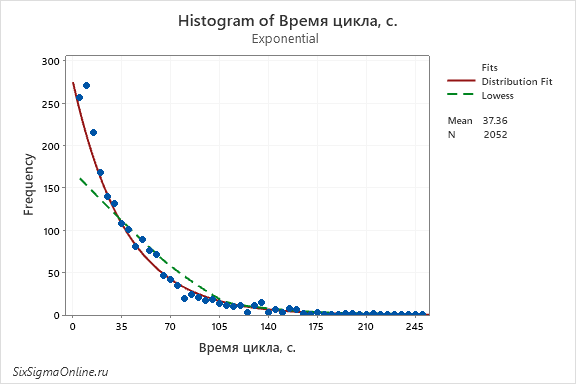
Программа автоматически аппроксимирует данные (в рассмотренном примере выбрано экспоненциальное распределение):

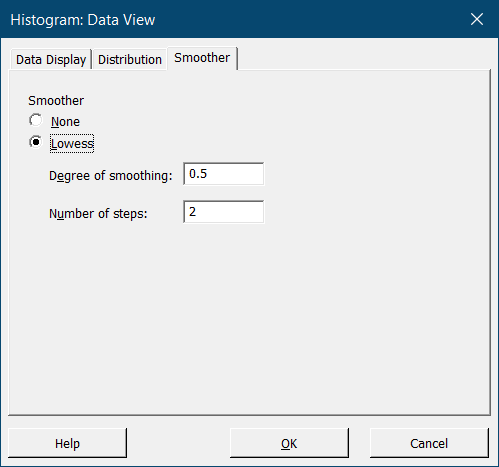
Мы также можем наложить на гистограмму сглаживающую кривую. Для этого выберите опцию Data View еще раз и в появившемся окне перейдите на закладку Smoother. Установите флажок напротив Lowess – это название алгоритма, который использует программа:

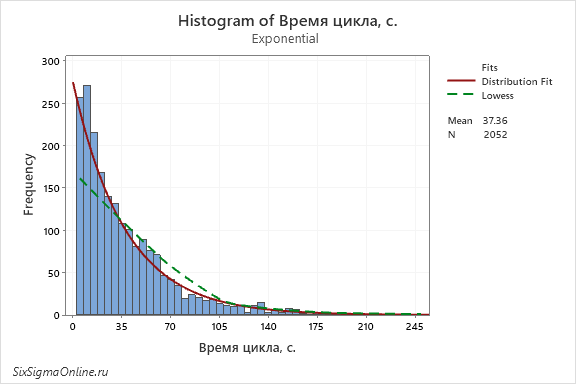
Параметры сглаживания – степень и количество шагов – оставляем по умолчанию: 0.5 и 2 соответственно. Полученная гистограмма выглядит следующим образом:

Варьируя этими значениями (степень сглаживания в пределах от 0 до 1), можно менять плавность, мягкость перепадов, приближённость к данным сглаживающей кривой, в зависимости от наших данных и цели анализа.

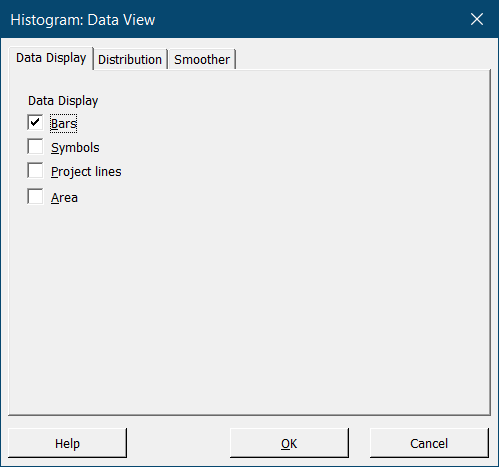
На вкладке Data Display окна Histogram: Data View можно выбрать различные, относительно нестандартные, способы представления данных на гистограмме:

Если вместо значения по умолчанию – Bars” (колонки) – установить флажок напротив Symbols (символы), частота появления наблюдений в каждом интервале будет представлена виде точек:

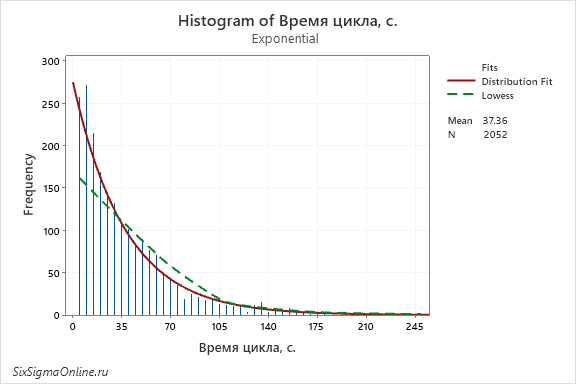
Опция Project lines (линии проекции) – позволяет представить данные в виде штрихов с длиной, соответствующей частоте появления значения (на оси X):

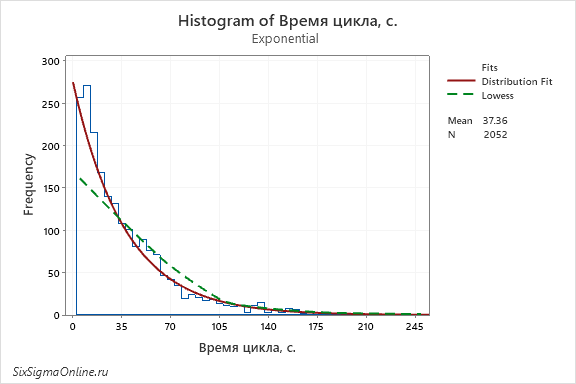
Опция Area (площадь) объединяет все прямоугольники данных, образуя единую площадь под кривой, очерченную контуром:

Обратите внимание, что флажки можно отмечать как по отдельности, так и в любых комбинациях. В таком виде гистограмма менее наглядна и, возможно, на первый взгляд покажется не столь понятной. С другой стороны, использование точек, к примеру, позволяет оценить, насколько точно данные аппроксимированы кривой распределения, а с помощью проекционных линий и обрамленных областей сравнить несколько массивов данных гораздо проще, чем с помощью стандартных “столбчатых” гистограмм.

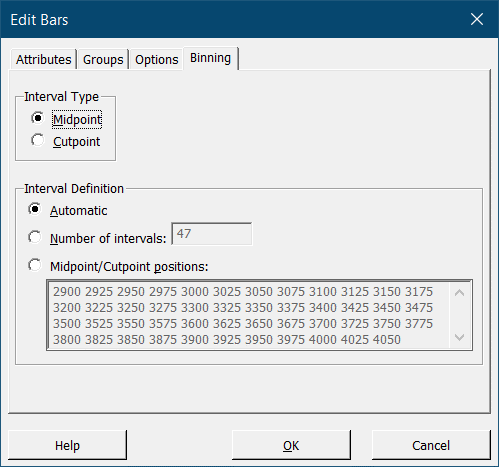
Кроме стандартных настроек, общих для всех графиков в Minitab (таких как настройка шкалы осей, цветов отдельных элементов графика, линий и границ), следует отметить настройку интервалов – Binning. Эта опция специфична для гистограмм. Чтобы перейти к настройке интервалов, дважды кликните на диаграмму – откроется окно редактирования графика. В нем следует дважды кликнуть либо по самой гистограмме, либо по оси данных (X). В открывшемся окне необходимо перейти на вкладку Binning:

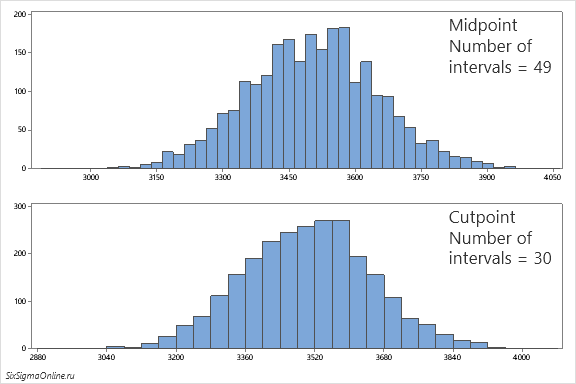
Настройки по умолчанию: Interval Type – Midpoint (значения по оси X будут расположены в центре частотных ячеек); Interval Definition – Automatic (количество интервалов определяется программой). Выбав Cutpoint в поле Interval Type, мы сдвигаем интервалы данных таким образом, что значения по оси X будут лежать в точках состыковки прямоугольников – интервалов данных, а установив флажок напротив Number of intervals в поле Interval Definition, можем задать необходимое количество интервалов для гистограммы.

Сравните: вместо Midpoint выбрана опция Cutpoint, а количество интервалов изменено с 47 по умолчанию до 30:

Как проводить анализ гистограмм?

Гистограммы нужны для того, чтобы наглядно представить распределение наблюдений. Но что еще мы можем увидеть, рассматривая прямоугольники, составляющие этот график? Какую информацию можем “прочесть”? На что обратить внимание и как это лучше сделать?

Визуальная оценка гистограмм позволяет воспринять ряд статистических показателей:

• распределение наблюдений (distribution);
• наибольшую концентрацию данных – моду (mode);
• минимальное и максимальное значения (min и max);
• размах (range);
• степень асимметрии – скос (skewness);
• эксцесс (kurtosis);
• наличие явных выбросов (outliers);
• возможное присутствие нескольких распределений (популяций);
• ширину интервалов – дистанцию между правым и левым краями частотной ячейки по оси X;
• количество интервалов – общее (в том числе и нулевые значения) количество частотных ячеек гистограммы.

Все это постараемся разобрать ниже.

Как уже неоднократно упоминалось в этой публикации, первое, что мы будем оценивать, глядя на гистограмму – это распределение наблюдений. Тут нет ничего сложного: мы просто визуально оцениваем, на какое из известных нам распределений похожа форма нашего графика. В проектах шести сигм чаще всего сравнивают сходство с нормальным законом распределения. Визуально оценивать согласие с любым другим законом сложно, но если вы возьметесь за это, посмотрите, как могут выглядеть различные Типы распределений и соответствующие им гистограммы.

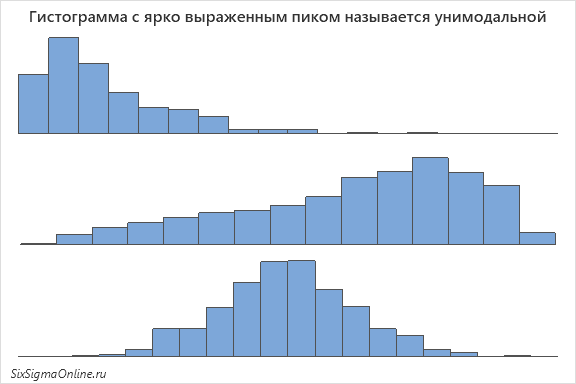
Гистограмма позволяет анализировать частотное распределение числового ряда, а соответственно дает возможность выделить наиболее вероятные число или интервал с наибольшим количеством наблюдений – другими словами, пик. Гистограмма с ярко выраженным пиком называется унимодальной:

Если мы можем различить у гистограммы два ярко выраженных пика, то гистограмма называется бимодальной. Во многих случаях это значит, что выборки происходят из двух разных популяций, так как наличие двух мод в одной популяции – маловероятное явление или присущее лишь некоторым процессам. Примеры таких процессов можно найти в публикациях О бимодальном распределении и полиэтилене низкого давления и Как получить бимодальное распределение?

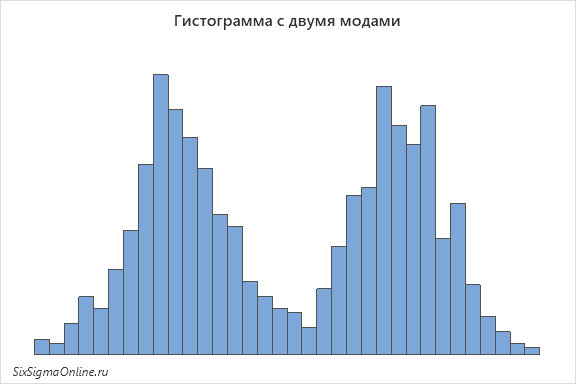
Гистограмма с двумя модами может выглядеть следующим образом:

И если вы получаете такое распределение по результатам входящего контроля качества, то, вероятнее всего, ваш поставщик отбирает лучшие детали, а вам посылает все остальное. Эта практика часто применяется в электронной промышленности: поставщик производит электронные компоненты, а на выходе своего процесса разделяет их на несколько групп в зависимости от того, насколько близко значение к номиналу.

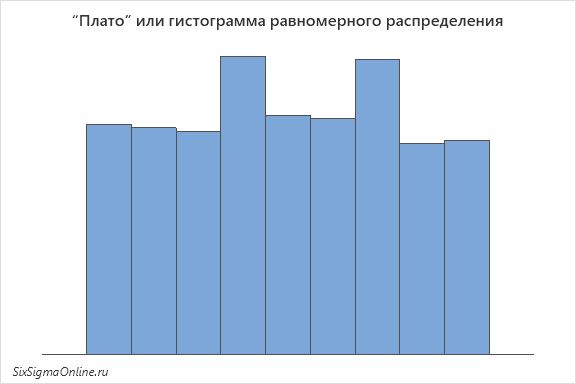
Гистограммы с тремя и большим количеством пиков (многомодальные) встречаются крайне редко и, зачастую, также свидетельствуют о присутствии специальных факторов, влияющих на исследуемую систему или процесс. Частный случай такого распределения – “плато” или гистограмма, каждый интервал которой содержит примерно равное количество значений. Такая гистограмма называется однородной или гистограммой равномерного распределения:

И если вы получаете такое распределение по результатам входящего контроля качества, то, вероятнее всего, ваш поставщик отбирает для вас лучшие детали, а все остальное посылает конкурентам.

Кроме количества пиков на гистограмме можно оценить его положение или симметрию. Гистограмма называется симметричной, если она имеет симметричную форму относительно центральной линии (правая и левая стороны одинаковой формы). Ассиметричные гистограммы бывают со скосом влево или вправо от осевой линии.

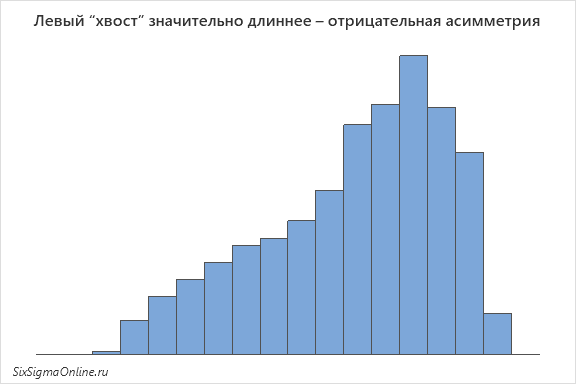
Если левая сторона гистограммы вытянута значительно больше, чем правая (или левый “хвост” значительно длиннее правого), то говорят, что гистограмма имеет отрицательную асимметрию:

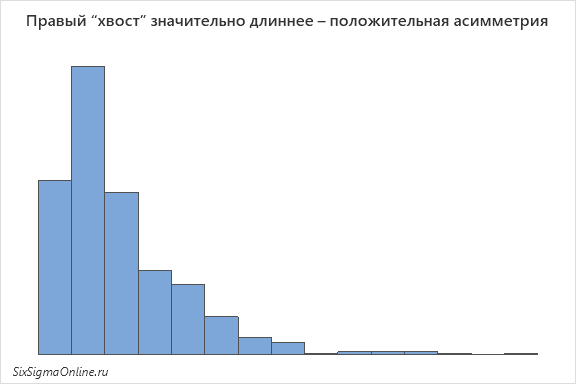
Соответственно, у гистограммы с положительной асимметрией больше в сторону выдаётся правая сторона (или правый “хвост” значительно длиннее левого):

Как представить данные на гистограмме?

Представление данных в виде диаграмм и графиков преследует одну цель: подать информацию в наглядном и понятном виде. Таким образом, важнейшими характеристиками любых диаграмм являются информативность и доступность тех данных, которые представлены с их помощью.

Несмотря на то, что гистограмма является достаточно простым и легким для восприятия графиком, представление данных с ее помощью требуют от исследователя определенного опыта, а от постороннего человека – понимания принципов построения и анализа гистограмм. Само собой разумеется, что гистограмма, построенная “своими руками”, будет понятна вам, но для человека, не знакомого с результатами наблюдений (или процессом, который описывают результаты наблюдений), ваш график может показаться не столь очевидным. Насколько построенная вами гистограмма будет информативна и понятна стороннему наблюдателю, определяет в конечном итоге то, как будет воспринята информация, которую вы показываете с ее помощью.

Как же построить такую гистограмму, которая гарантирует, что преподносимая с ее помощью информация, будет понятна всем?

Во-первых, не следует пренебрегать атрибутами стандартного графика: название гистограммы, величины и размерности осей X и Y – это первое, на что обращает внимание опытный исследователь. В этой публикации вы можете найти несколько примеров того, как гистограмма обращала ваше внимание на данные:

И того, как гистограмма заставляла вас совершенно забыть о данных, воспринимая ее лишь как иллюстрацию сказанному:

Во-вторых, представляя данные в виде гистограммы, вы должны быть уверены, что этот тип диаграмм наилучшим образом отражает ту информацию, которую вы пытаетесь показать. К примеру, разница между столбчатой диаграммой (Bar Chart) и гистограммой базируется в основном на различии представляемых типов данных. Выше мы подробно рассмотрели отличие гистограмм от других графиков. Надеюсь, это вам поможет понять, когда гистограмма не подойдет для представления имеющихся у вас данных.

В-третьих, не пренебрегайте дополнительными возможностями программного обеспечения. Большинство пакетов статистической обработки данных содержит встроенную функцию расчета описательных статистик и вывода графического отчета. В Mintab выберите Stat \ Basic Statistics \ Graphical Summary, чтобы получить такой график:

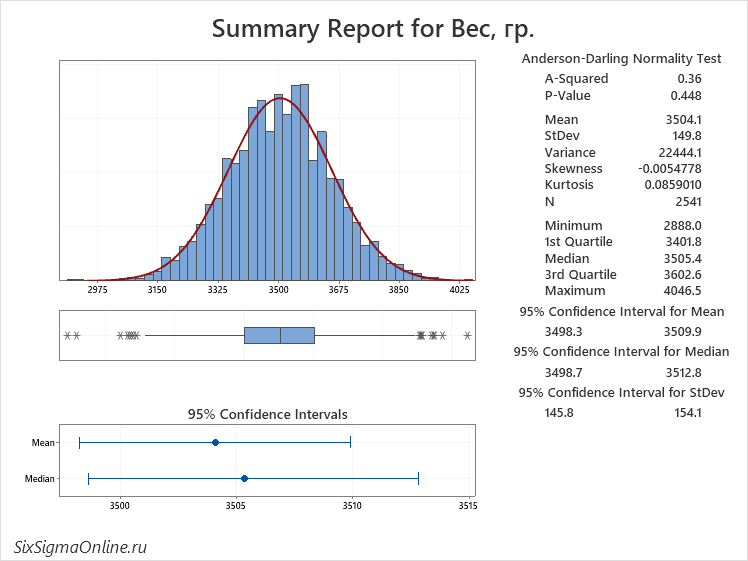
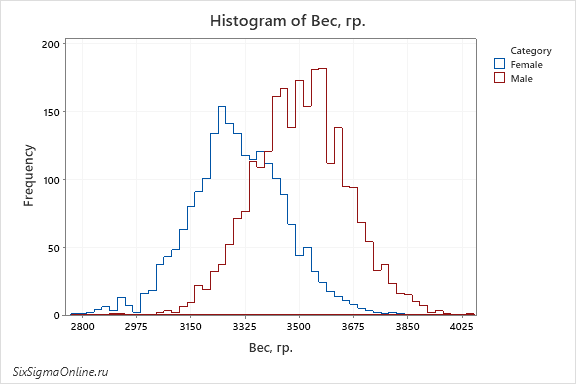
Глядя на полученный результат, вы можете увереннее интерпретировать данные:

1. Гистограмма конечно же напоминает “перевернутый колокол” и довольно точно вписывается в аппроксимирующую кривую нормального распределения, но теперь мы с определенной долей вероятности (p=0.448) можем утверждать, что наблюдения подчиняются нормальному закону распределения 2 .
2. Мы можем не только оценить, где находиться самый высокий столбик, но и прочесть величину среднего арифметического (Mean=3504.1) и медианы (Median=3505.4). Мы также видим, насколько перекрываются доверительные интервалы этих показателей ни графике ниже (95% Confidence Intervals).
3. Нам доступны показатели минимального (Minimum=2888.0) и максимального (Maximum=4046.5) значений. На диаграмме нет размаха, но есть величина стандартного отклонения (StDev=149.8).
4. Эксцесс (Kurtosis)– числовая характеристика степени остроты пика – близок к 0 (0,00859).
5. Показатель асимметрии – скос (Skewness) равен -0,005 – это очень близко к нулю.
6. Мы не видим выбросы на гистограмме, однако об их возможном наличии свидетельствует ящичная диаграмма ниже.
7. Обнаружить доказательства присутствия наблюдений из различных популяций нам не удалось: на диаграмме четко выражен один пик, и хоть он не содержит среднее арифметическое и медиану, его интервал находится в пределах доверительных интервалов этих статистик.
8. Исходя из смещения среднего арифметического относительно медианы и медианы относительно моды, а также пункта 5, можно было бы сделать вывод о наличии незначительной отрицательной асимметрии. Однако наблюдаемое явление скорее всего является следствием ограниченного количества наблюдений, а также влияния возможных выбросов.

Как сравнивать разные массивы данных с помощью гистограмм?

Выше мы рассмотрели общие принципы построения гистограмм и некоторые тонкости представления данных с их помощью. В этом разделе мы разберем, как сравнить гистограммы двух и более групп данных в Minitab.

Может показаться очевидным, но для того, чтобы сравнивать гистограммы различных групп данных, они должны быть:

• Перед глазами – вы не сможете сравнивать две гистограммы, перекликивая из одного окна в другой.
• Представлены в одной системе координат.

Этого можно добиться несколькими путями в Minitab:

1. Вы можете построить 2 гистограммы и разместить их рядом. Вам также понадобится изменить шкалу по умолчанию (как минимум по оси X), чтобы сравнение было корректным. Как строить простые гистограммы и устанавливать значения шкал, мы рассмотрели выше, поэтому опустим технические детали. Тем более, что этот способ самый трудоемкий и подходит для сравнения максимум 4-х графиков – больше на один экран не влезет.
2. Вы можете построить простую гистограмму, но автоматизировать все остальные операции. Для этого:
   • В меню Garph выберите Histogram, а затем Simple.
   • В появившемся окне задайте все колонки с наблюдениями, которые собираетесь сравнить, в поле Graph variables (переменные).
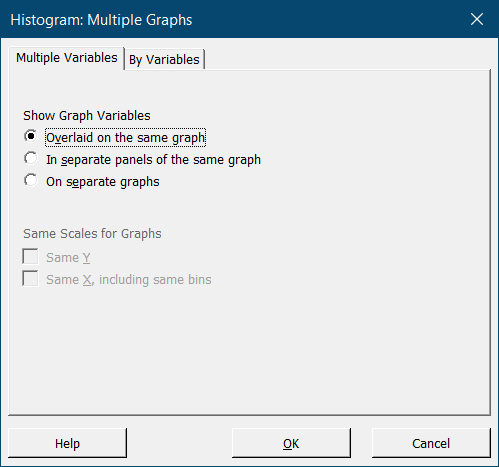
   • Затем нажмите кнопку Multiple Graphs (несколько графиков) и выберите опцию Overlaid on the same graph. Это позволит нанести все переменные на один график.
     • Опция по умолчанию – on separate graphs – строит отдельную гистограмму для каждой переменной.
     • Опция in separate panels of the same graph размещает все переменные на одном графике, но выделяет каждой из них в отдельную гистограмму. Получается график из отдельных “плиточек”. Чтобы построенные таки образом гистограммы находились в одной системе координат, не забудьте установить флажки ниже: Same Y (равные значения по оси Y) и Same X, including same bins (равные значения по оси X, включая равные интервалы).

Этот способ подойдет, когда вам необходимо сравнить данные в разных колонках. Если же несколько массивов данных находятся в одной колонке (а именно в таком виде чаще всего удается получить результаты из базы данных производственной системы), используйте третий вариант.

Вы можете выбрать в меню Graph \ Histogram одну из опций, которые мы не рассматривали до сих пор: With Groups (простая гистограмма для различных групп данных) или With Fit and Groups (гистограмма для различных групп данных с наложенной кривой распределения).

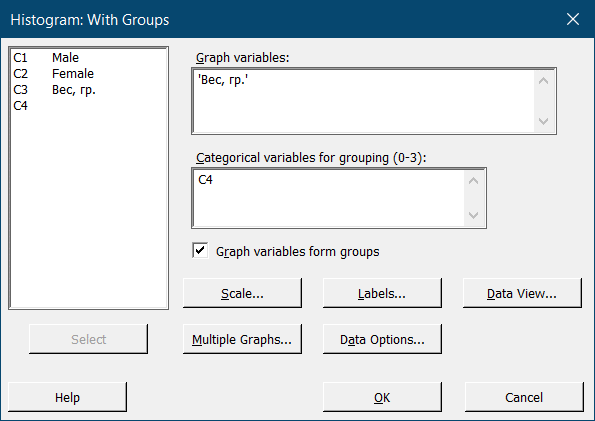
• Выберем With Groups инажмем Ok.
• В поле “Graph variables:” необходимо задать столбцы значений, которые мы хотим сравнить.
  • Опция “Graph variables form groups” по умолчанию отмечена флажком. Если вы задали одну колонку переменных, то различий не будет, а вот для двух и более колонок гистограммы будут построены в двух разных окнах.
• В поле “Categorical variables for grouping (0-3)” указываем колонку или колонки с атрибутами для группирования наблюдений.

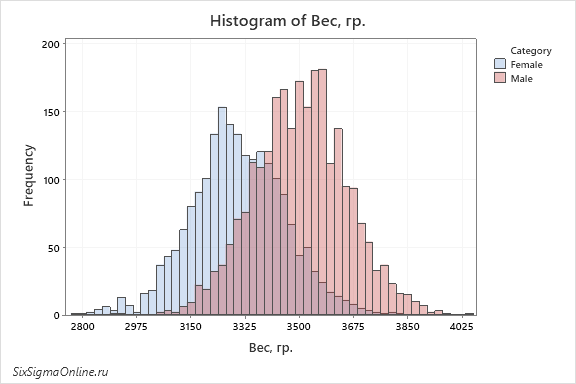
• Нажимаем Ok и получаем две гистограммы:

По умолчанию построенная гистограмма будет состоять из полупрозрачных обрамленных колонок 3 , цвет которых соответствует отдельному массиву данных. Тем не менее, вид гистограммы можно изменить:

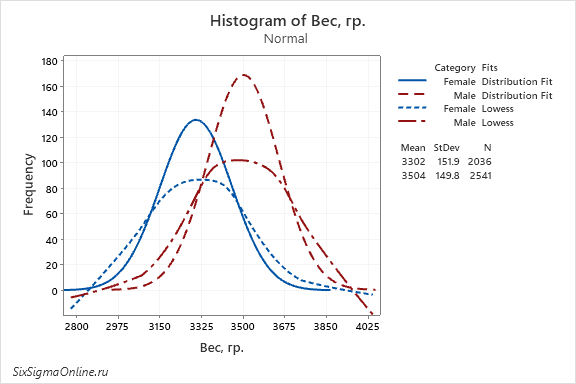
• Добавить линии аппроксимированных распределений данных и сглаживания: дважды кликните по диаграмме, чтобы открыть окно редактирования; затем кликните правой кнопкой мыши и выберите Add \ Distribution Fit и/или Add \ Smoother. Сами колонки можно удалить с графика.

• Представить данные не колонками (bars), а символами (symbols), линиями (project lines) или площадью (area): дважды кликните по диаграмме, чтобы открыть окно редактирования; затем кликните правой кнопкой мыши и выберите Add \ Data Display и выберите нужную опцию.

Все остальные настройки и способы кастомизации, специфические для гистограмм и общие для всех графиков в Minitab, также доступны. Этого спектра более чем достаточно для сравнения данных и визуализации ваших выводов. Однако вы должны понимать, что происхождение данных, что они обозначают и цели анализа программе неизвестны. Именно поэтому настройка и оформление гистограмм проводится вручную. Множество дополнительных опций, в том числе изменение цветовых гамм, типов и толщины линий, изменений форм и размеров фигур, являются, безусловно, очень полезными при построении и оформлении гистограмм. Главное – не переусердствовать и всегда сохранять понимание того, что является одним из основных преимуществ гистограмм – простота и доступность понимания как для вас, так и для того, кому вы её представляете.

______________________________________
1 Подробнее о типах данных, а также отличии атрибутивных от непрерывных данных читайте в статье Типы данных.
2 Статистически грамотнее было бы сказать, что мы не можем отклонить гипотезу о подчинении распределения наблюдений нормальному закону. В тексте статьи использовано не совсем точное, однако более понятное выражение, которое отнюдь не меняет полученный вывод. Прим. ред.
3 На самом деле внешний вид будет зависеть от версии Minitab, которую вы используете. Прим. ред.

Источник