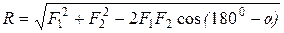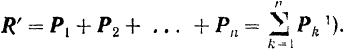Геометрический способ сложения сходящихся сил
Системой сходящихся сил называется система сил, линии действия которых пересекаются в одной точке. Две силы, сходящиеся в одной точке, согласно третьей аксиоме статики можно заменить одной силой – равнодействующей.
Решение многих задач статики связано с операцией сложения векторов, в частности, сил.
Главный вектор системы сил – величина, равная геометрической сумме сил системы. Главный вектор системы сил не следует путать с равнодействующей. Равнодействующая – всегда главный вектор, а главный вектор равен равнодействующей, если система сил является сходящейся.
Равнодействующую плоской системы сходящихся сил можно определить графически и графоаналитически.
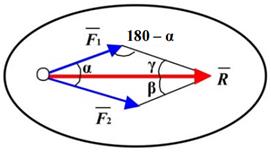
Сложение двух сил. При графическом определении равнодействующей на чертеже и выбранном масштабе изображаются силы, затем они складываются по правилу параллелограмма. По длине диагонали параллелограмма, учитывая выбранный масштаб, определяется равнодействующая, равная сумме слагаемых сил. Точность определения равнодействующей зависит в этом случае от точности построения силового треугольника.
Графоаналитический способ сложения сил позволяет более точно определить равнодействующую, используя тригонометрические зависимости:
или 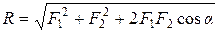
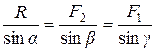
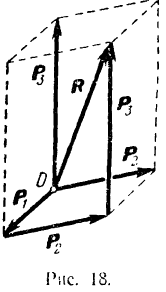
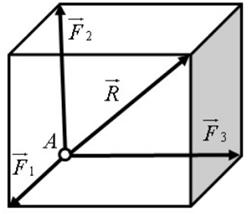
Сложение трех сил, не лежащих в одной плоскости: геометрическую сумму 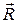
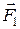
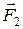
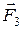
 |  |
| Рис. 1.19 | Рис. 1.20 |
Сложение системы сил. Сложение плоской системы сходящихся сил осуществляется либо путём последовательного сложения сил с построением промежуточной равнодействующей (рис.1.21), либо путём построения силового многоугольника (рис.1.22).
Источник
Геометрический способ сложения сходящихся сил
Геометрический способ сложения сходящихся сил
Системой сходящихся сил называется система сил, линии действия которых пересекаются в одной точке (рис. 15,а). Если мы перенесем все силы такой системы но линиям их действия в общую точку пересечения этих
линии, то, согласно первому следствию из аксиом статики, действие системы на абсолютно твердое тело не изменится. Таким образом, любую систему сходящихся сил можно заменить эквивалентной системой сил, приложенных в одной точке.
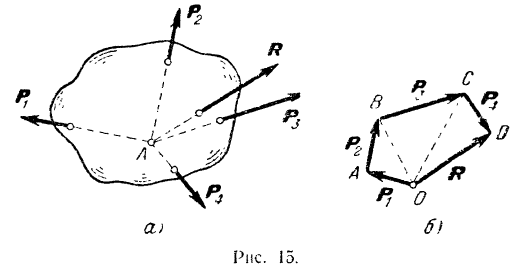
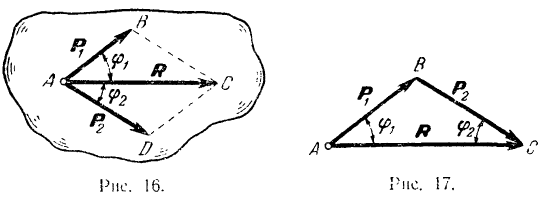
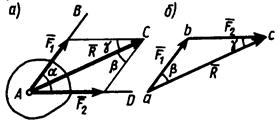
Задача о сложении двух сил, приложенных к одной точке, геометрически решается построением соответствующего параллелограмма сил (рис. 16) или силового треугольника (рис. 17), изображающего одну из половин параллелограмма.
Для построения силового треугольника из конца вектора одной силы 
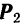
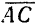
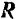
Последовательно применяя правило треугольника, можно найти равнодействующую любого числа сходящихся сил, например четырех сил 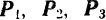
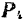
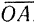
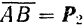

Полученный многоугольник 
Очевидно, что равнодействующая 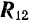
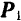
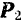
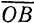
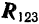
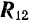
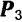
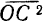
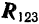
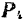
Правило сложения сходящихся сил по способу многоугольника является общим правилом сложения любых векторов и называется их геометрическим сложением.
Геометрическая сумма всех сил любой системы называется главным вектором 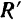
Таким образом, можно сказать, что равнодействующая 
Геометрическая сумма векторов не зависит от перемены мест слагаемых и, следовательно, при изменении порядка сложения сил их главный векгор не изменяется.
В частном случае трех сходящихся сил 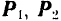
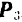
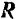
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Возможно вам будут полезны эти дополнительные темы:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник
Геометрический способ сложения сил
Сложение сил.
Система сходящихся сил
Главным вектором системы сил называют геометрическую сумму сил системы.
Сложение двух сил. Геометрическая сумма 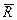
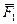
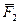
Модуль равнодействующей силы
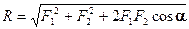 . . | (1.3) |
где α – угол между силами.
Углы, которые сила образует со слагаемыми силами, определяются из уравнения
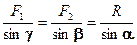 . . | (1.4) |
Рисунок 1.15 – Сложение двух сил: а – по правилу параллелограмма; б – построением силового треугольника
Сложение трёх сил, не лежащих в одной плоскости. Геометрическая сумма 
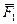
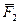
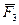
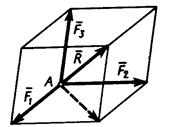 | Рисунок 1.16 – Сложение трёх сил, не лежащих в одной плоскости |
Сложение системы сил.Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил 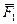
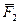
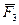
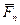
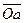
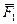
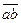
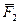
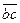
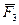
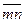
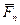
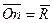
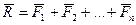 или или 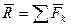 . . | (1.5) |
 | Рисунок 1.17 – Система сходящихся сил и её геометрическая сумма (главный вектор) 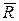 , являющийся равнодействующей , являющийся равнодействующей |
Равнодействующая сходящихся сил,т.е. сил, линии действия которых пересекаются в одной точке (рис. 1.17, а).
Т.к. сила, действующая на абсолютно твёрдое тело, является вектором скользящим, то система сходящихся сил эквивалентна системе сил, приложенных в одной точке (на рис. 1.17, а в точке А). Последовательно применяя закон параллелограмма сил, придём к выводу, что система сходящихся сил имеет равнодействующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке пересечения их линий действия. Следовательно, система сил 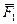
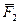
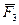
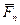
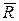
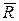
В задачах механики система сходящихся сил может быть приложена к материальной точке массой m, тогда равнодействующая сила 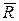
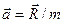
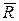

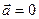
Все силы, приложенные к точке, являются сходящимися, поэтому собственное вращение материальной точки не рассматривается. Чтобы изменить вращение твёрдого тела, к нему надо приложить не сходящуюся систему сил. Если на твёрдое тело действует только сходящаяся система сил, то состояние вращения твёрдого тела не изменяется.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник