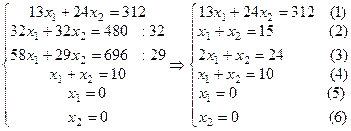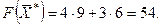Графический (геометрический) метод решения задач ЛП
Пример 6.1. Решить следующую задачу ли-нейного программирования геометрическим методом:
.
Решение:
Задача линейного программирования задана в стандартной форме и имеет два проектных параметра, следовательно
, воз-можно ее решение геометрическим методом.
1 этап: построение прямых, ограничивающих область допустимых решений ( ОДР).
Рассмотрим систему ограничений задачи линейного програм-мирования (для удобства пронумеруем неравенства):
Рассмотрим первое ограничение, заменим знак неравенства знаком равенства и выразим переменную х2 через х1:
.
Для построения прямой по данному уравнению зададим две произвольные точки, к примеру:
Аналогично определяем точки для остальных ограничений системы и строим по ним прямые, соответствующие каждому неравенству (рис. 1). Прямые пронумеруем согласно принятой ранее схеме.
2 этап: определение решения каждого из нера-венств системы ограничений.
Определим полуплоскости – решения каждого из неравенств.
Рассмотрим первое неравенство системы ограничений задачи. Возьмем какую-либо точку (контрольную точку), не принадлежащую соответствующей данному неравенству прямой, например, точку (0; 0). Подставим ее в рассматриваемое неравенство:
.
При подстановке координат контрольной точки неравенство остается справедливым. Следовательно, множество точек, принадлежащих данной прямой (т.к. неравенство не строгое), а также расположенных ниже ее, будут являться решениями рассматриваемого неравенства (пометим на графике (рис. 1) найденную полуплоскость двумя стрелками направленными вниз рядом с прямой I) .
Аналогично определяем решения других неравенств и соответственно помечаем их графике. В результате график примет следующий вид:
3 этап: определение ОДР задачи линейного про- граммирования.
Найденные полуплоскости (решения каждого из неравенств системы ограничений) при пересечении образуют многоугольник ABCDEO, который и является ОДР рассматриваемой задачи.
Рис. 1. Область допустимых решений задачи
4 этап: построение вектора-градиента.
Вектор-градиент показывает направление максимизации целевой функции . Определим его координаты: координаты начальной его точки (точки приложения) – (0; 0), координаты второй точки:
Построим данный вектор на графике (рис. 2).
5 этап: построение прямой целевой функ-ции.
Рассмотрим целевую функцию данной задачи:
.
Зададим ей какое-либо значение, к примеру, 
. Выразим переменную х2 через х1:
.
Для построения прямой по данному уравнению зададим две произвольные точки, к примеру:
Построим прямую соответствующую целевой функции (рис. 2).
Рис. 2. Построение целевой функции F(X) и вектора-градиента С
6 этап: определение максимума целевой функ-ции.
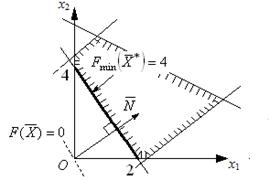
Перемещая прямую F(X) параллельно са-мой себе по направлению вектора-градиента, определяем крайнюю точку (точки) ОДР. Согласно графику (рис. 3), такой точкой является точка С – точка пересечения прямых I и II.
Рис. 3. Определение точки максимума целевой функции F(X)
Определим координаты точки С, с этой целью, решим сле-дующую систему линейных уравнений:
Подставим найденные координаты в целевую функцию и найдем ее оптимальное (максимальное) значение:
Ответ: при заданных ограничениях макси-мальное значение целевой функции F(Х)=24, которое достигается в точке С, координаты которой х1=6, х2=4.
Пример 6.2. Решить задачу линейного про- граммирования геометрическим методом:
Решение:
Этапы 1-3 аналогичны соответствующим этапам предыдущей задачи.
4 этап: построение вектора-градиента.
Построение вектора-градиента осуществляется аналогично, как и в предыдущей задаче. Построим данный вектор на графике (рис. 4). Отметим также на данном графике стрелкой направление, обратное вектору-градиенту, – направление минимизации целевой функцииF (X).
5 этап: построение прямой целевой функ-ции.
Построение прямой целевой функции F(X) осуществляется аналогично, как и в предыдущей задаче (результат построения приведен на рис. 4).
Рис. 4. Построение целевой функции F(x) и вектора-градиента С
6 этап: определение оптимума целевой функ-ции.
Перемещая прямую F(x) параллельно са-мой себе в направлении, обратном вектору-градиенту, опреде-ляем крайнюю точку (точки) ОДР. Согласно графику (рис. 5), та- кой точкой является точка О с координатами (0; 0).
Рис. 5. Определение точки минимума целевой функции
Подставляя координаты точки минимума в целевую функ-цию, определяем ее оптимальное (минимальное) значение, которое равно 0.
Ответ: при заданных ограничениях минимальное значение целевой функции F(Х)=0, которое достигается в точке О (0; 0).
Пример 6.3. Решить следующую задачу ли-нейного программирования геометрическим методом:
Решение:
Рассматриваемая задача линейного программирования задана в канонической форме, выделим в качестве базисных переменные x 1 и x2.
Составим расширенную матрицу и выделим с помощью метода Жордана- Гаусса базисные переменныеx1 и x 2.
Умножим (поэлементно) первую строку на –3 и сложим со вто-рой: 
.
Умножим вторую строку на 
:
.
Сложим вторую с первой строкой:
.
В результате система ограничений примет следующий вид:
Выразим базисные переменные через свободные:
Выразим целевую функцию также через свободные перемен-ные, для этого подставим полученные значения базисных переменных в целевую функцию:
.
Запишем полученную задачу линейного программирования:
Так как переменные x1 и x2 неотрицательные, то полученную систему ограничений можно записать в следующем виде:
Тогда исходную задачу можно записать в виде следующей эк- вивалентной ей стандартной задаче линейного программирования:
Данная задача имеет два проектных параметра, следовательно, возможно ее решение геометрическим мето-дом.
1 этап: построение прямых, ограничивающих область допустимых решений ( ОДР).
Рассмотрим систему ограничений задачи линейного програм-мирования (для удобства пронумеруем неравенства):
Построим прямые, соответствующие каждому неравенству (рис. 6). Прямые пронумеруем согласно принятой ранее схе-ме.
2 этап: определение решения каждого из нера-венств системы ограничений.
С помощью контрольных точек определим полуплоскости – решения каждого из неравенств, и пометим их на графике (рис. 6) с помощью стрелок.
3 этап: определение ОДР задачи линейного про- граммирования.
Найденные полуплоскости (т.е. решения каждого из неравенств системы ограничений) не имеют общего пересечения (так решения неравенства I противоречат в целом остальным неравенствам системы ограничений), следовательно, система ограничений не совместна и задача линейного программирования в силу этого не имеет решения.
Рис. 6. Фрагмент MathCAD-документа:
построение области допустимых решений задачи
Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности системы ограничений.
Если после подстановки координат контрольной точки в неравенство его смысл нарушается, то решением данного неравенства является полуплоскость не содержащая данную точку (т.е. расположенная по другую сторону прямой).
Направление, обратное вектору-градиенту, соответствует направлению минимизации целевой функции.
Источник
Геометрический метод решения ЗЛП
Геометрический метод решения ЗЛП применяется в случае, если задача содержит не более двух переменных или может быть сведена к таковой.
Каждое из неравенств системы ограничений геометрически определяет полуплоскость допустимых значений переменных с граничными прямыми.
Алгоритм геометрического метода:
1. В системе ограничений знаки неравенств заменяются на знаки точных равенств и по полученным уравнениям строятся прямые на плоскости x1Ox2.
2. Определяются полуплоскости – области решения неравенств, и строится многоугольник решений (ОДР), который получается в результате пересечения полуплоскостей. Стороны этого многоугольника являются прямыми уравнений системы ограничений.
4. Из точки (0; 0) строится вектор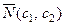 
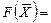
, направление которого определяет направление возрастания целевой функции 
c1x1 + c2x2.
5. Строится начальная прямая (линия нулевого уровня) целевой функции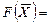 
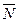
c1x1 + c2x2 = 0, которую передвигают в направлении вектора 
до крайней угловой точки многоугольника решений. В этой точке целевая функция принимает max значение.
6. Определяются координаты точки максимума целевой функции 
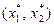
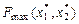
как точки пересечения соответствующих прямых и вычисляется значение целевой функции в этой точке 
.
В нашем случае система уравнений будет иметь вид:
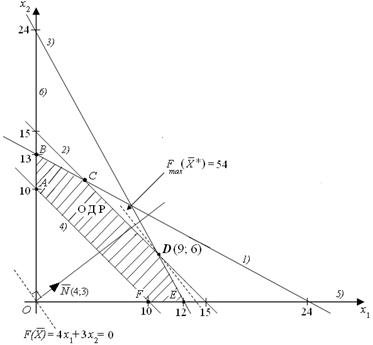
Построим по полученным уравнениям прямые и пронумеруем их (рис.1). Областью ОДР будет выпуклый многоугольник АBCDEF, каждая вершина которого является опорным планом. Из точки (0; 0) строим вектор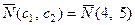 
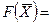
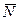
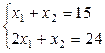
. Начальная линия уровня будет иметь вид: 
4x1 + 3x2 = 0. Перемещая линию уровня вдоль вектора 
, получим, что функция F принимает max значение в точке D – самой крайней справа вершине многоугольника ОДР. Точка D является точкой пересечения прямых (2) и (3). Находим координаты точки D, решая систему уравнений этих прямых:
.
Решением системы будут значения x1 = 9, x2 = 6, т.е. D(9; 6). Тогда 
Рис. 1. Иллюстрация геометрического метода решения ЗЛП
Таким образом, решением задачи будет оптимальный план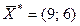 
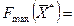
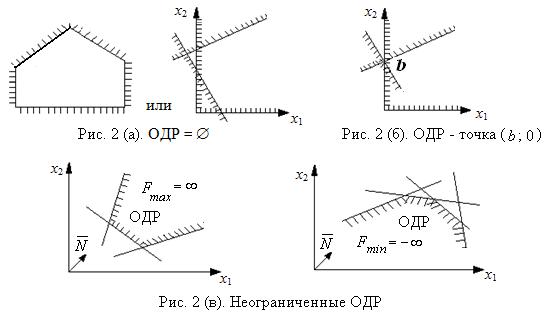
, дающий max значение функции 
54 у.е. Максимальная прибыль 54 у.е. достигается при изготовлении 9 единиц изделий I вида и 6 единиц изделий II вида.
В данной задаче ОДР является выпуклый многоугольник. Однако возможны и следующие случаи:
1) ОДР – пустое множество (рис.2, а). В этом случае задача линейного программирования не имеет решения из-за несовместности системы ограничений.
2) ОДР – единственная точка, которая и будет единственным и оптимальным решением (рис.2, б).
3) ОДР – выпуклая неограниченная область (рис.2, в). В задаче на max оптимальное решение не существует, если целевая функция не ограничена сверху (Fmax = ∞). В задаче на min оптимальное решение не существует, если целевая функция не ограничена снизу (Fmin = –∞).
4) Может оказаться, что линия уровня функции F совпадает с одной из сторон многоугольника ОДР (экстремум целевой функции достигается на всем отрезке между двумя соседними вершинами ОДР) (рис.3). Тогда имеет место альтернативный оптимум: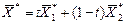 
, где t є [0; 1] – параметр.
Рис. 3. Альтернативный оптимум
Формы записи задачи линейного программирования
Существуют три формы записи ЗЛП: каноническая, стандартная, общая.
В канонической (основной) форме все ограничения имеют вид уравнений, т.е.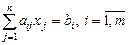 
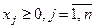
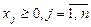
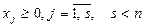
, а также условие неотрицательности накладывается на все переменные: 
. В стандартной форме все ограничения записаны в виде нестрогих неравенств, и также 
. В общей формеограничения могут быть представлены как уравнениями, так и неравенствами, а условие неотрицательности может накладываться не на все, а только на часть переменных 
.
Источник
