Геометрический способ решения дифференциальных уравнений
дЙЖЖЕТЕОГЙБМШОЩН ХТБЧОЕОЙЕН ОБЪЩЧБЕФУС ХТБЧОЕОЙЕ, УЧСЪЩЧБАЭЕЕ ОЕЪБЧЙУЙНХА РЕТЕНЕООХА x , ЙУЛПНХА ЖХОЛГЙА y(x) Й РТПЙЪЧПДОХА ЙУЛПНПК ЖХОЛГЙЙ.
уЙНЧПМЙЮЕУЛЙ ДЙЖЖЕТЕОГЙБМШОПЕ ХТБЧОЕОЙЕ НПЦОП ОБРЙУБФШ ФБЛ
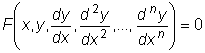
оЕЙЪЧЕУФОПК ЪДЕУШ СЧМСЕФУС ЖХОЛГЙС y , ЧИПДСЭБС РПД ЪОБЛ РТПЙЪЧПДОЩИ (ЙМЙ ДЙЖЖЕТЕОГЙБМПЧ).
еУМЙ ЙУЛПНБС ЖХОЛГЙС y(x) ЕУФШ ЖХОЛГЙС ПДОПК ОЕЪБЧЙУЙНПК РЕТЕНЕООПК, ФП ДЙЖЖЕТЕОГЙБМШОПЕ ХТБЧОЕОЙЕ ОБЪЩЧБЕФУС ПВЩЛОПЧЕООЩН . ч ЬФПК ЗМБЧЕ НЩ ВХДЕН ТБУУНБФТЙЧБФШ ФПМШЛП ПВЩЛОПЧЕООЩЕ ДЙЖЖЕТЕОГЙБМШОЩЕ ХТБЧОЕОЙС.
рПТСДЛПН ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС ОБЪЩЧБЕФУС РПТСДПЛ ОБЙЧЩУЫЕК РТПЙЪЧПДОПК, ЧИПДСЭЕК Ч ХТБЧОЕОЙЕ.
оБРТЙНЕТ, ХТБЧОЕОЙЕ
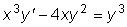
ЕУФШ ХТБЧОЕОЙЕ РЕТЧПЗП РПТСДЛБ, Б ХТБЧОЕОЙЕ
— ХТБЧОЕОЙЕ ЧФПТПЗП РПТСДЛБ.
тЕЫЕОЙЕН ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС ОБЪЩЧБЕФУС ЧУСЛБС ЖХОЛГЙС y(x), ЛПФПТБС ВХДХЮЙ РПДУФБЧМЕООПК Ч ХТБЧОЕОЙЕ, ПВТБЭБЕФ ЕЗП Ч ФПЦДЕУФЧП. тЕЫЕОЙЕ ЕЭЕ ОБЪЩЧБЕФУС ЙОФЕЗТБМПН ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС.
рТЙНЕТ
тБУУНПФТЙН ХТБЧОЕОЙЕ 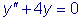
жХОЛГЙС 
дЕКУФЧЙФЕМШОП,
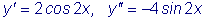
Й ХТБЧОЕОЙЕ ПВТБЭБЕФУС Ч ФПЦДЕУФЧП: 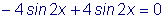
тЕЫЕОЙЕН ТБУУНБФТЙЧБЕНПЗП ХТБЧОЕОЙС ВХДХФ Й ЖХОЛГЙЙ
Й ЧППВЭЕ ЖХОЛГЙЙ 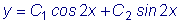

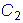
ч УБНПН ДЕМЕ
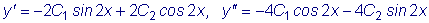
Й ХТБЧОЕОЙЕ ПВТБЭБЕФУС Ч ФПЦДЕУФЧП 
ъБНЕФЙН, ЮФП ТБУУНБФТЙЧБЕНПЕ ХТБЧОЕОЙЕ ЙНЕЕФ ВЕУЮЙУМЕООПЕ НОПЦЕУФЧП ТЕЫЕОЙК ЧЙДБ: 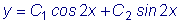
тЕЫЕОЙЕ ДЙЖЖЕТЕОГЙБМШОЩИ ХТБЧОЕОЙК РЕТЧПЗП РПТСДЛБ
дЙЖЖЕТЕОГЙБМШОЩН ХТБЧОЕОЙЕН РЕТЧПЗП РПТСДЛБ ОБЪЩЧБЕФУС ХТБЧОЕОЙЕ, УЧСЪЩЧБАЭЕЕ ОЕЪБЧЙУЙНХА РЕТЕНЕООХА x , ЙУЛПНХА ЖХОЛГЙА y(x) Й РТПЙЪЧПДОХА РЕТЧПЗП РПТСДЛБ ЙУЛПНПК ЖХОЛГЙЙ.
дЙЖЖЕТЕОГЙБМШОПЕ ХТБЧОЕОЙЕ РЕТЧПЗП РПТСДЛБ ЙНЕЕФ ЧЙД 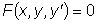
пВЭЕЕ Й ЮБУФОПЕ ТЕЫЕОЙЕ
пВЭЙН ТЕЫЕОЙЕН ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС РЕТЧПЗП РПТСДЛБ ОБЪЩЧБЕФУС ТЕЫЕОЙЕ 



тБЧЕОУФЧП ЧЙДБ 
ъБНЕФЙН, ЮФП Ч РТБЛФЙЛЕ ЮБЭЕ ЧУЕЗП ВЩЧБЕФ ОХЦОЩН ОЕ ПВЭЕЕ ТЕЫЕОЙЕ, Б ФБЛ ОБЪЩЧБЕНПЕ ЮБУФОПЕ ТЕЫЕОЙЕ ,ПФЧЕЮБАЭЕЕ ПРТЕДЕМЕООЩН ОБЮБМШОЩН ХУМПЧЙСН, ЧЩФЕЛБАЭЙН ЙЪ ХУМПЧЙС ДБООПК ЛПОЛТЕФОПК ЪБДБЮЙ.
юБУФОЩН ТЕЫЕОЙЕН ОБЪЩЧБЕФУС МАВБС ЖХОЛГЙС 



ъБДБЮБ ПФЩУЛБОЙС ТЕЫЕОЙС ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС y I = f(x,y) , ХДПЧМЕФЧПТСАЭЕЗП ЪБДБООЩН ОБЮБМШОЩН ХУМПЧЙСН y(xo ) = yo, ОБЪЩЧБЕФУС ЪБДБЮЕК лПЫЙ .

еУМЙ ЖХОЛГЙС f(x,y) — РТБЧБС ЮБУФШ ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС y I = f(x,y) — ОЕРТЕТЩЧОБ Ч ОЕЛПФПТПК ЪБНЛОХФПК ПВМБУФЙ D РМПУЛПУФЙ xOy Й ЙНЕЕФ Ч ЬФПК ПВМБУФЙ ПЗТБОЙЮЕООХА ЮБУФОХА РТПЙЪЧПДОХА f I y (x,y), ФП ЛБЦДПК ЧОХФТЕООЕК ФПЮЛЕ ПВМБУФЙ D УППФЧЕФУФЧХЕФ, Й РТЙФПН ЕДЙОУФЧЕООПЕ, ТЕЫЕОЙЕ, ХДПЧМЕФЧПТСАЭЕЕ ОБЮБМШОЩН ХУМПЧЙСН.
рТЙНЕТ
тБУУНПФТЙН ХТБЧОЕОЙЕ
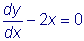
пВЭЙН ТЕЫЕОЙЕН ЬФПЗП ХТБЧОЕОЙС СЧМСЕФУС УЕНЕКУФЧП ЖХОЛГЙК
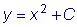
дЕКУФЧЙФЕМШОП, РТЙ МАВПН ЪОБЮЕОЙЙ C ЬФБ ЖХОЛГЙС ХДПЧМЕФЧПТСЕФ ХТБЧОЕОЙА: 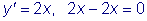
лТПНЕ ФПЗП, ЧУЕЗДБ НПЦОП ОБКФЙ ФБЛПЕ ЪОБЮЕОЙЕ C, ЮФП УППФЧЕФУФЧХАЭЕЕ ЮБУФОПЕ ТЕЫЕОЙЕ ВХДЕФ ХДПЧМЕФЧПТСФШ ЪБДБООПНХ ОБЮБМШОПНХ ХУМПЧЙА.
оБКДЕН, ОБРТЙНЕТ, ЮБУФОПЕ ТЕЫЕОЙЕ, ХДПЧМЕФЧПТСАЭЕЕ ОБЮБМШОПНХ ХУМПЧЙА y(1)=-2. рПДУФБЧМСС ЬФЙ ЪОБЮЕОЙС Ч ХТБЧОЕОЙЕ 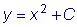
РПМХЮЙН 
тЕЫБС ЬФП ХТБЧОЕОЙЕ ПФОПУЙФЕМШОП C РПМХЮЙН C = — 3.
уМЕДПЧБФЕМШОП, ЙУЛПНЩН ЮБУФОЩН ТЕЫЕОЙЕН ВХДЕФ ЖХОЛГЙС: Y = X 2 — 3.
ьФП ТЕЫЕОЙЕ НПЦОП РПМХЮЙФШ, ЙУРПМШЪХС ОЙЦЕРТЙЧЕДЕООЩК БРРМЕФ ДМС РПУФТПЕОЙС РПМС ОБРТБЧМЕОЙК Й ЙОФЕЗТБМШОЩИ ЛТЙЧЩИ ДМС ХТБЧОЕОЙС РЕТЧПЗП РПТСДЛБ.
у ЗЕПНЕФТЙЮЕУЛПК ФПЮЛЙ ЪТЕОЙС ПВЭЕЕ ТЕЫЕОЙЕ ХТБЧОЕОЙС РЕТЧПЗП РПТСДЛБ РТЕДУФБЧМСЕФ УПВПК УЕНЕКУФЧП ЛТЙЧЩИ ОБ РМПУЛПУФЙ xOy , ЪБЧЙУСЭЕЕ ПФ ПДОПК РТПЙЪЧПМШОПК РПУФПСООПК C . ьФЙ ЛТЙЧЩЕ ОБЪЩЧБАФУС ЙОФЕЗТБМШОЩНЙ ЛТЙЧЩНЙ ДБООПЗП ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС.
юБУФОПНХ ТЕЫЕОЙА УППФЧЕФУФЧХЕФ ПДОБ ЙОФЕЗТБМШОБС ЛТЙЧБС, РТПИПДСЭБС ЮЕТЕЪ ОЕЛПФПТХА ЪБДБООХА ФПЮЛХ. фБЛ, Ч РПУМЕДОЕН РТЙНЕТЕ ПВЭЕЕ ТЕЫЕОЙЕ ЗЕПНЕФТЙЮЕУЛЙ ЙЪПВТБЪЙФУС УЕНЕКУФЧПН РБТБВПМ, РТЙЮЕН ЛБЦДПНХ ЪОБЮЕОЙА РБТБНЕФТБ C ВХДЕФ УППФЧЕФУФЧПЧБФШ ЧРПМОЕ ПРТЕДЕМЕООБС ЛТЙЧБС. юБУФОПЕ ТЕЫЕОЙЕ ЙЪПВТБЪЙФУС РБТБВПМПК (ТЙУ. 1. 


тЕЫЙФШ ЙМЙ РТПЙОФЕЗТЙТПЧБФШ ДБООПЕ ДЙЖЖЕТЕОГЙБМШОПЕ ХТБЧОЕОЙЕ ЬФП ЪОБЮЙФ:
Б) ОБКФЙ ЕЗП ПВЭЕЕ ТЕЫЕОЙЕ ЙМЙ ПВЭЙК ЙОФЕЗТБМ, ЕУМЙ ОЕ ЪБДБОЩ ОБЮБМШОЩЕ ХУМПЧЙС,
В) ОБКФЙ ЮБУФОПЕ ТЕЫЕОЙЕ, ХДПЧМЕФЧПТСАЭЕЕ ЪБДБООЩН ОБЮБМШОЩН ХУМПЧЙСН.

| рХУФШ ДБОП ДЙЖЖЕТЕОГЙБМШОПЕ ХТБЧОЕОЙЕ, ТБЪТЕЫЕООПЕ ПФОПУЙФЕМШОП РТПЙЪЧПДОПК: рТЙНЕТ тБУУНПФТЙН ХТБЧОЕОЙЕ фЕПТЕНБ УХЭЕУФЧПЧБОЙС Й ЕДЙОУФЧЕООПУФЙ ТЕЫЕОЙС ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС. тБУУНБФТЙЧБС ХТБЧОЕОЙЕ РЕТЧПЗП РПТСДЛБ Источник |

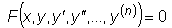


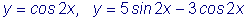
 .
.  ПРТЕДЕМСЕФ ЪОБЮЕОЙЕ РТПЙЪЧПДОПК
ПРТЕДЕМСЕФ ЪОБЮЕОЙЕ РТПЙЪЧПДОПК  , Ф.Е. ПРТЕДЕМСЕФ ХЗМПЧПК ЛПЬЖЖЙГЙЕОФ ЛБУБФЕМШОПК Л ЙОФЕЗТБМШОПК ЛТЙЧПК, РТПИПДСЭЕК ЮЕТЕЪ ЬФХ ФПЮЛХ.
, Ф.Е. ПРТЕДЕМСЕФ ХЗМПЧПК ЛПЬЖЖЙГЙЕОФ ЛБУБФЕМШОПК Л ЙОФЕЗТБМШОПК ЛТЙЧПК, РТПИПДСЭЕК ЮЕТЕЪ ЬФХ ФПЮЛХ.  .
.  , Ф.Е. УПЧРБДБЕФ У ХЗМПЧЩН ЛПЬЖЖЙГЙЕОФПН РТСНПК, РТПИПДСЭЕК ЮЕТЕЪ ОБЮБМП ЛППТДЙОБФ Й ФПЮЛХ У ЛППТДЙОБФБНЙ (x,y). пЮЕЧЙДОП, ЮФП ЙОФЕЗТБМШОЩНЙ ЛТЙЧЩНЙ ВХДХФ РТСНЩЕ y=Cx, ЗДЕ C — РТПЙЪЧПМШОБС РПУФПСООБС, Ф.Л. ОБРТБЧМЕОЙЕ ЬФЙИ РТСНЩИ ЧУАДХ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН РПМС.
, Ф.Е. УПЧРБДБЕФ У ХЗМПЧЩН ЛПЬЖЖЙГЙЕОФПН РТСНПК, РТПИПДСЭЕК ЮЕТЕЪ ОБЮБМП ЛППТДЙОБФ Й ФПЮЛХ У ЛППТДЙОБФБНЙ (x,y). пЮЕЧЙДОП, ЮФП ЙОФЕЗТБМШОЩНЙ ЛТЙЧЩНЙ ВХДХФ РТСНЩЕ y=Cx, ЗДЕ C — РТПЙЪЧПМШОБС РПУФПСООБС, Ф.Л. ОБРТБЧМЕОЙЕ ЬФЙИ РТСНЩИ ЧУАДХ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН РПМС.  ЮБУФОПЗП ТЕЫЕОЙС, ХДПЧМЕФЧПТСАЭЕЗП ЬФПНХ ХУМПЧЙА.
ЮБУФОПЗП ТЕЫЕОЙС, ХДПЧМЕФЧПТСАЭЕЗП ЬФПНХ ХУМПЧЙА.  .
.  , Б ЙОФЕЗТБМШОЩНЙ ЛТЙЧЩНЙ — УЕНЕКУФЧП ЗЙРЕТВПМ, РТЙЮЕН ЮЕТЕЪ ЛБЦДХА ФПЮЛХ
, Б ЙОФЕЗТБМШОЩНЙ ЛТЙЧЩНЙ — УЕНЕКУФЧП ЗЙРЕТВПМ, РТЙЮЕН ЮЕТЕЪ ЛБЦДХА ФПЮЛХ  , ОЕ МЕЦБЭХА ОБ ПУЙ Oy РТПИПДЙФ ПДОБ Й ФПМШЛП ПДОБ ЙОФЕЗТБМШОБС ЛТЙЧБС, Ф.Е. ТБУУНБФТЙЧБЕНПЕ ХТБЧОЕОЙЕ ЙНЕЕФ ЕДЙОУФЧЕООПЕ ТЕЫЕОЙЕ, РТПИПДСЭЕЕ ЮЕТЕЪ ФПЮЛХ, ОЕ МЕЦБЭХА ОБ ПУЙ Oy , ОП ПОП ОЕ ЙНЕЕФ ТЕЫЕОЙС, РТПИПДСЭЕЗП ЮЕТЕЪ ФПЮЛХ, ЧЪСФХА ОБ ПУЙ Oy .
, ОЕ МЕЦБЭХА ОБ ПУЙ Oy РТПИПДЙФ ПДОБ Й ФПМШЛП ПДОБ ЙОФЕЗТБМШОБС ЛТЙЧБС, Ф.Е. ТБУУНБФТЙЧБЕНПЕ ХТБЧОЕОЙЕ ЙНЕЕФ ЕДЙОУФЧЕООПЕ ТЕЫЕОЙЕ, РТПИПДСЭЕЕ ЮЕТЕЪ ФПЮЛХ, ОЕ МЕЦБЭХА ОБ ПУЙ Oy , ОП ПОП ОЕ ЙНЕЕФ ТЕЫЕОЙС, РТПИПДСЭЕЗП ЮЕТЕЪ ФПЮЛХ, ЧЪСФХА ОБ ПУЙ Oy . 
 СЧМСЕФУС ПВЭЙН ТЕЫЕОЙЕН ЬФПЗП ХТБЧОЕОЙС, Б РТЙ МАВПН ЪОБЮЕОЙЙ C РТСНБС
СЧМСЕФУС ПВЭЙН ТЕЫЕОЙЕН ЬФПЗП ХТБЧОЕОЙС, Б РТЙ МАВПН ЪОБЮЕОЙЙ C РТСНБС  , ПФЧЕЮБЕФ УМЕДХАЭБС ФЕПТЕНБ.
, ПФЧЕЮБЕФ УМЕДХАЭБС ФЕПТЕНБ. 


