Геометрический способ построения вида

Черчение

Способы построения видов на чертеже

Построение видов начинается с мысленного выбора положе­ния детали перед плоскостями проекций. Затем выбирают коли­чество видов, необходимых и достаточных для выявления формы детали, а также способ их построения.

Выбор положения детали в системе плоскостей проекций за­висит от ее рабочего положения, способа изготовления на произ­водстве, формы. Например, если деталь изготавливается на то­карном станке, то на чертеже ее ось вращения должна распола­гаться горизонтально.

Виды чертежа могут быть выполнены различными способами. Рассмотрим некоторые из них.

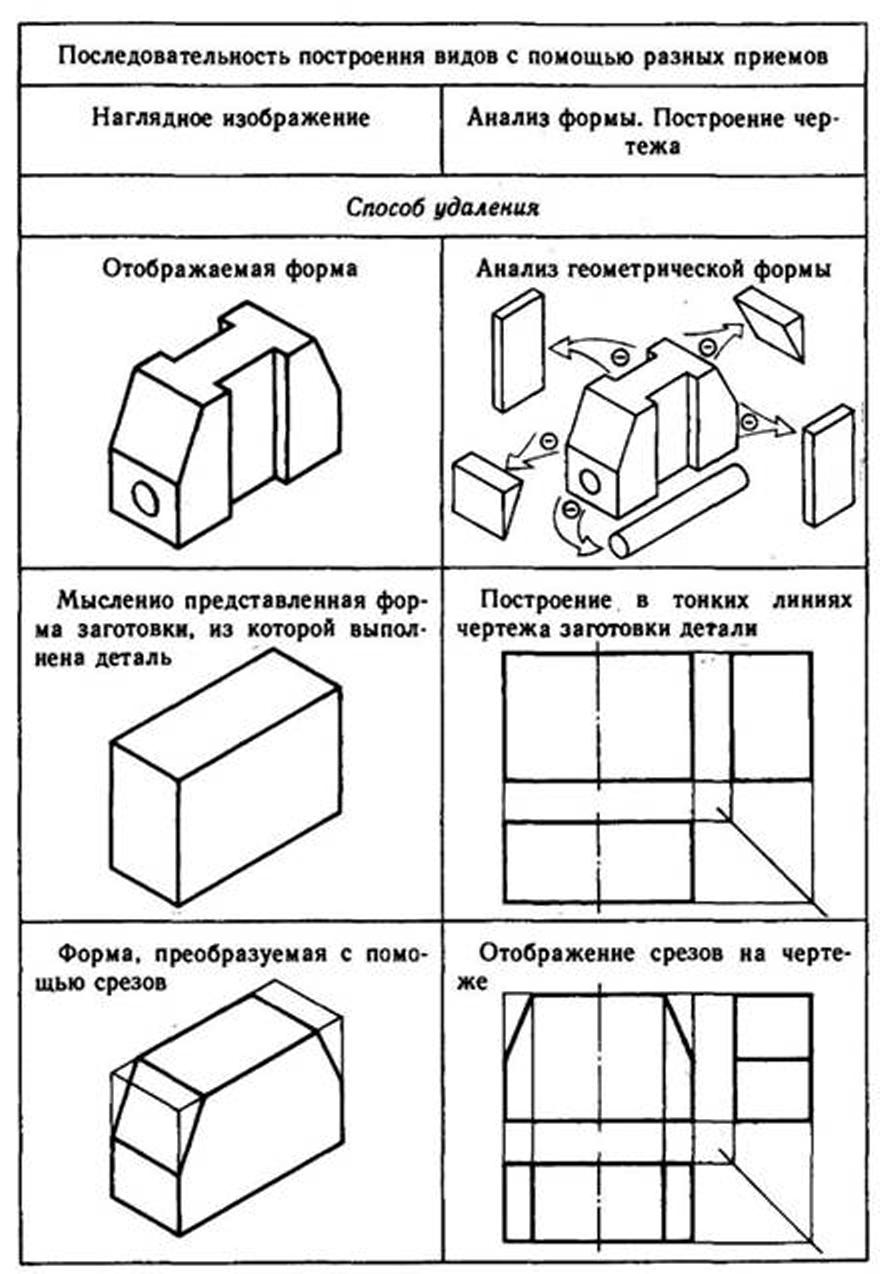
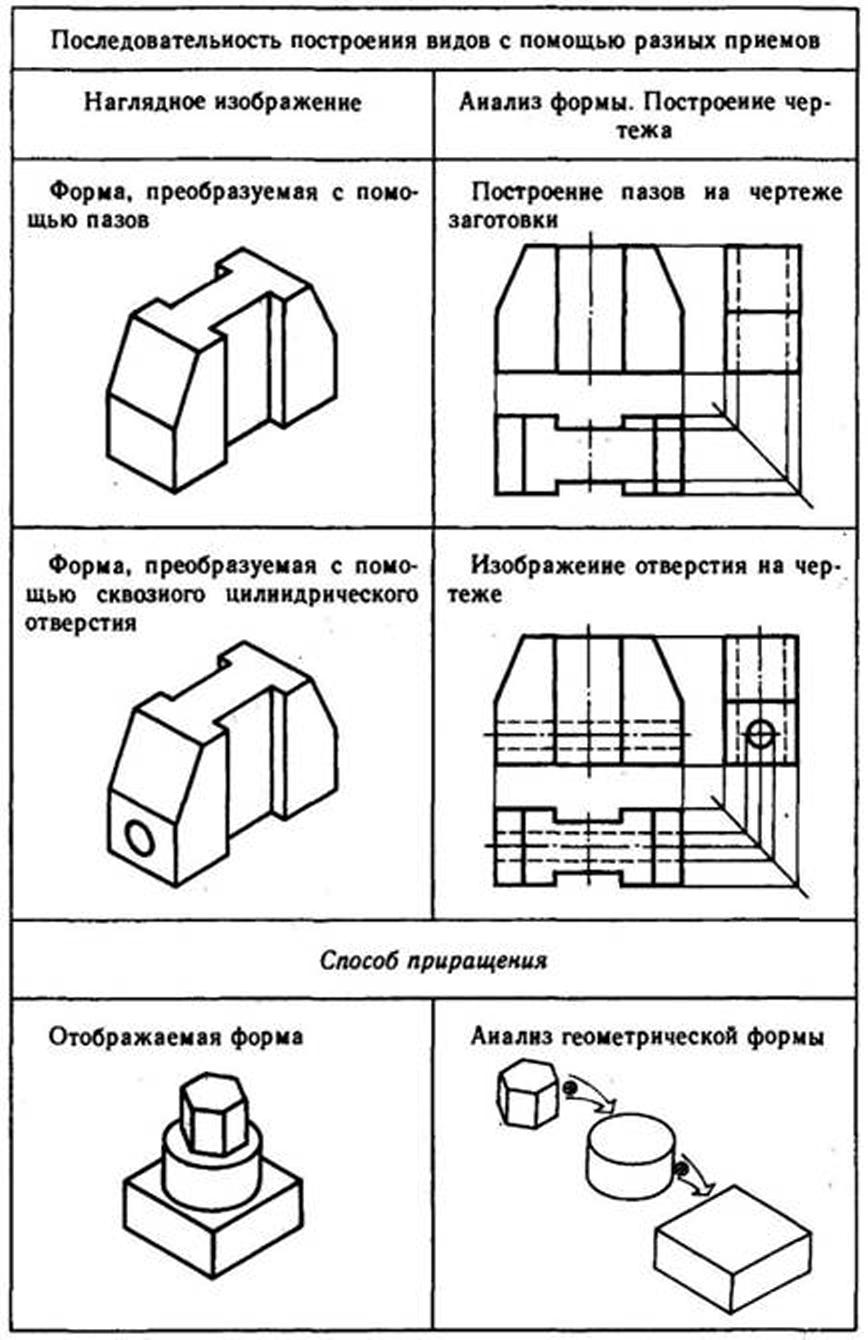
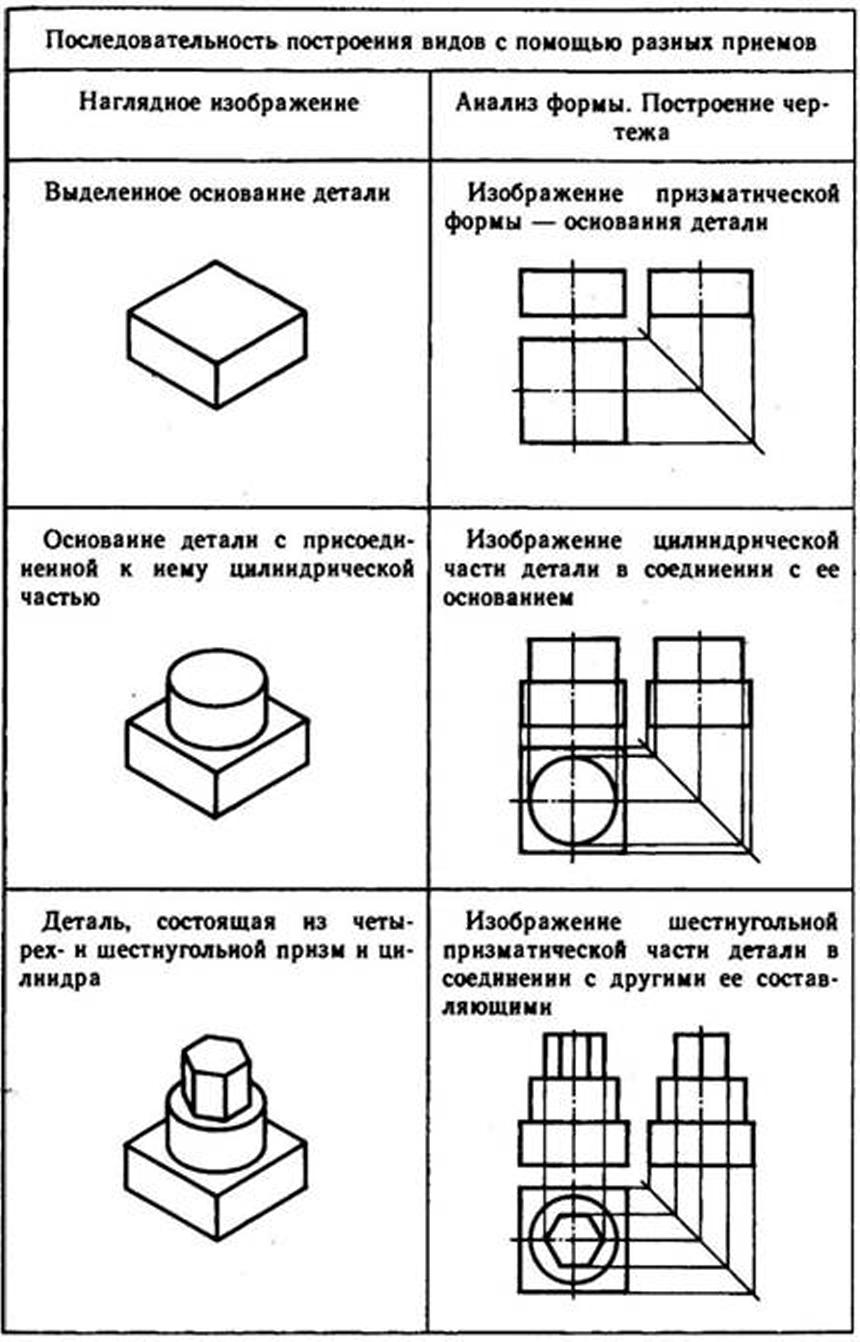
Построение видов на основе последовательного вычерчива­ния геометрических тел, составляющих форму предмета. Для того чтобы выполнить чертеж этим способом, необходимо мысленно разделить деталь на составляющие ее простые геометри­ческие тела, выяснив, как они расположены относительно друг друга. Затем нужно выбрать главный вид детали и число изо­бражений, позволяющие понять ее форму и последовательно изобразить одно геометрическое тело за другим до полного ото­бражения формы объекта. Необходимо соблюдать размеры фор­мы и правильно ориентировать ее элементы относительно друг друга (табл. 8).

Построение видов на основе поэлементного вычерчивания геометрических тел, составляющих форму предмета, осуществля­ется с помощью приемов удаления и приращения.

При вычерчивании геометрического тела с использованием приема удаления на чертеже последовательно изменяется форма заготовки с помощью удаления объемов схожих с приемами ее обработки точением, сверлением, фрезерованием и т. п.

При вычерчивании геометрического тела с использованием приема приращения объемы элементов изделия как бы допол­няют друг друга, приращиваются.

8. Поэлементное вычерчивание геометрических тел, составляющих форму предмета

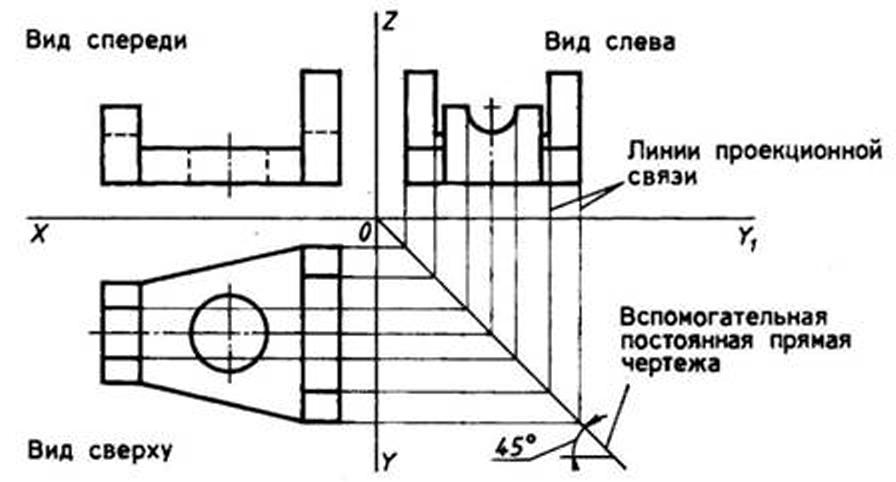
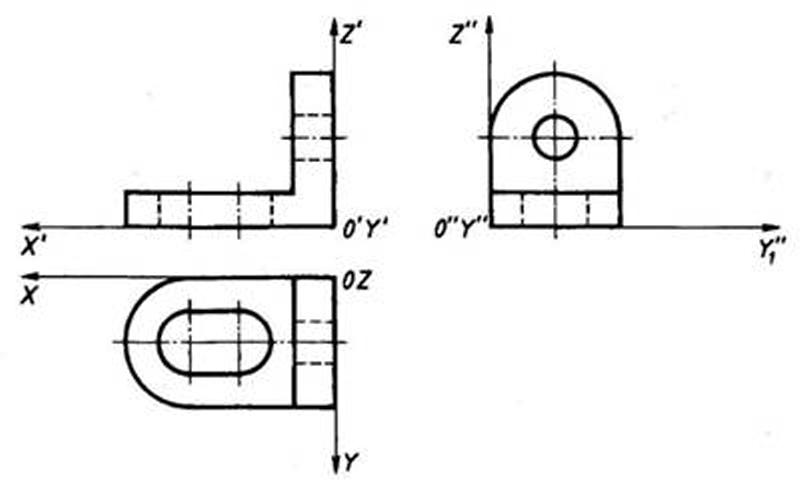
Построение видов с помощью постоянной прямой чертежа (способ внешнего координирования). Постоянной прямой чер­тежа называют линию, которую проводят из центра координат (точки О) вниз направо под углом 45° (рис. 86).

Предмет мысленно размещают в системе плоскостей проек­ций. Оси плоскостей проекций принимают за координатные оси. Проекционную связь между видом сверху и видом слева осуще­ствляют с помощью линий проекционной связи, которые прово­дят до пересечения с постоянной прямой чертежа и строят под углом 90° друг к другу.

Постоянную прямую чертежа, как правило, используют в тех случаях, когда по двум заданным видам необходимо построить третий вид детали (см. рис. 86). Перечертив два вида детали, строят постоянную прямую чертежа и проводят линии проекци­онной связи параллельно оси ОХ до пересечения с постоянной прямой чертежа, а затем — параллельно оси OZ.

Рассмотренный способ построения называют способом внеш­него координирования, поскольку предмет фиксируется в про­странстве относительно осей плоскостей проекций, которые рас­полагаются вне изображаемого объекта.

(Если на чертеже не показаны оси проекций и необходи­мо выполнить третий вид детали, то можно построить постоян­ную прямую чертежа в любом месте с правой стороны от вида сверху.)

Построение видов с помощью внутреннего координирования объекта. Внутреннее координирование заключается в мысленном введении дополнительных осей координат, привязанных к проецируемому предмету.

Рис. 86. Построение третьей проекции по двум заданным с помощью постоянной прямой чертежа

Рис. 87. Построение видов способом внутреннего координирования объекта

Источник

Геометрические построения

Геометрическим построением называют способ решения задачи, при котором ответ получают в основном графическим путём без каких — либо математических расчетов.

Деление отрезка прямой на равные части

Из концов отрезка А и В циркулем проводят две дуги окружности радиусом R, несколько большим половины отрезка, до взаимного пересечения в точках а и в. Через полученные точки а и в проведем прямую, которая пересекает отрезок АВ в точке С, делящей отрезок на две равные части.
Проделав подобные построения для отрезков АС и СВ, получим точки D и F. Точки С, D и F делят отрезок АВ на четыре равные части.

Деление отрезка прямой на произвольное число равных частей

Такое деление основано на свойстве подобных треугольников. На рис. в показано деление отрезка АВ на девять равных частей.

Через любой конец отрезка АВ под произвольным углом к нему (лучше острым) проводим вспомогательную прямую. С помощью циркуля от точки А на вспомогательной прямой прямой откладываем девять произвольных, но равных между собой отрезков. Последнюю точку 9 соединяем с точкой В, а через остальные точки 1, 2, …, 8 проводим прямые, параллельные прямой В9 до пересечения с отрезком АВ. Точки пересечения разделят отрезок АВ на девять равных частей.

Построение перпендикуляра из данной точки к прямой

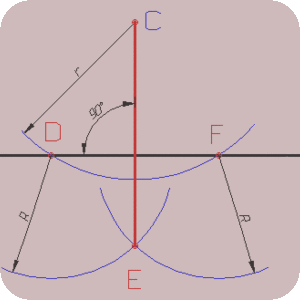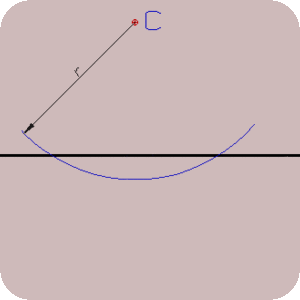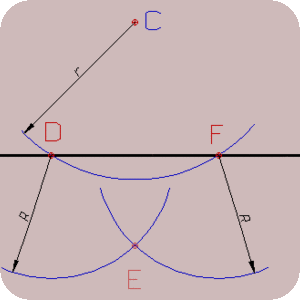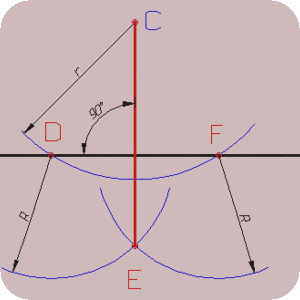
Из данной точки С проводят дугу окружности произвольного радиуса так чтобы она пересекала прямую, заданную отрезком АВ, в точках D и F. Из этих точек описывают две дуги окружности радиусом R, несколько большим половины отрезка DF, до пересечения в точке Е. Точки С и Е соединяют прямой которая и будет искомым перпендикуляром.

Деление угла на две равные части

Деление прямого угла АВС на три равные части выполняется в следующей последовательности:

1. Из вершины угла проводят дугу окружности произвольного радиуса R до пересечения со сторонами угла в точках D и F;

2. Из полученных точек проводят две дуги тем же радиусом R, до взаимного пересечения пересечения с дугой DF в точках К и М;

3. Точки К и М соединяют с вершиной В прямыми, которые разделят угол АВС на три равные части.

Деление прямого угла на три равные части

Деление прямого угла АВС на три равные части выполняется в следующей последовательности:

1. Из вершины угла проводят дугу окружности произвольного радиуса R до пересечения со сторонами угла в точках D и F;

2. Из полученных точек проводят две дуги тем же радиусом R, до взаимного пересечения пересечения с дугой DF в точках К и М;

3. Точки К и М соединяют с вершиной В прямыми, которые разделят угол АВС на три равные части.

Построение угла равного заданному

Пусть задан угол АВС. Требуется построить такой же угол, но со сторонойDE и вершиной в точке D. Для этого из вершины В данного угла проведем дугу окружности произвольного радиуса R, которая пересечет стороны угла в точках 1 и 2. Из вершины D искомого угла тем же радиусом R проведем дугу окружности, которая пересечет отрезок DE в точке 3. Из точки 3 проведем дугу радиусом r, равным отрезку 12, до пересечения с ранее проведенной дугой радиуса R в точке 4. Через полученную точку 4 и точку D проводим недостающую сторону искомого угла.

Деление окружности на три, шесть и двенадцать равных частей

Деление окружности на три, шесть и двенадцать равных частей выполняется в следующей последовательности:

1. Выбираем в качестве точки 1, точку пересечения осевой линии с окружностью;

2. Из точки 4 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 2 и 3;

3. Точки 1, 2 и 3 делят окружность на три равные части;

4. Из точки 1 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 5 и 6;

5. Точки 1 — 6 делят окружность на шесть равных частей;

6. Дуги радиусом R, проведенные из точек 7 и 8 пересекут окружность в точках 9, 10, 11 и 12;

7. Точки 1 — 12 делят окружность на двенадцать равных частей.

Деление окружности на пять равных частей

Деление окружности на пять равных частей выполняется в следующей последовательности:

1. Из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В;

2. Из точки В опускают перпендикуляр на горизонтальную осевую линию;

3. Из основания перпендикуляра — точки С, радиусом равным С1, проводят дугу окружности, которая пересечет горизонтальную осевую линию в точке D;

4. Из точки 1 радиусом равным D1, проводят дугу до пересечения с окружностью в точке 2, дуга 12 равна 1/5 длины окружности;

5. Точки 3, 4 и 5 находят откладывая циркулем по данной окружности хорды, равные D1.

Деление окружности на семь равных частей

Деление окружности на семь равных частей выполняется в следующей последовательности:

1. Из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В;

2. Из точки В опускают перпендикуляр на горизонтальную осевую линию;

3. Длину перпендикуляра ВС откладывают от точки 1 по окружности семь раз и получают искомые точки 1 — 7.

Деление окружности на восемь равных частей

Деление окружности на восемь равных частей производится в следующей последовательности:

1. Проводят две перпендикулярные оси, которые пересекая окружность в точках 1,2,3,4 делят ее на четыре равные части;

2. Применяя известный прием деления прямого угла на две равные части при помощи циркуля или угольника строят биссектрисы прямых углов, которые пересекаясь с окружностью в точках 5, 6, 7, и 8 делят каждую четвертую часть окружности пополам.

Сопряжения

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Далее рассмотрим основные типы сопряжений.

Сопряжение прямого угла

Cкругление прямого угла, имеющего вершину О, дугой радиуса R осуществляется в следующей последовательности:
1. Из вершины О проводят дугу заданным радиусом R, до пересечения со сторонами угла в точках А и В (точки сопряжения);
2. Центр скругления О1 должен находится на геометрическом месте точек, равноудаленных от сторон угла, т.е. на биссектрисе угла АОВ и определяется точкой пересечения дуг радиуса R, проведенных из точек сопряжения А и В;
3. Проводят дугу АВ радиусом R и центром О1.

Сопряжение острого угла

Скругление острого угла дугой радиуса R можно выполнить в следующей последовательности:
1. Геометрическим местом точек, равноудаленных от сторон угла, будут являться прямые, параллельные сторонам угла и проходящие от них на расстоянии R;
2. Точка пересечение этих прямых определяет центр скругления О1;
3. Пересечение перпендикуляров опущенных из центра скругления со сторонами определят положение точек сопряжения А и В;
4. Поводим дугу АВ из центра О1 радиусом R.

Сопряжение тупого угла

Скругление тупого угла производится точно так же, как и острого. Можно несколько изменить ход построения, если воспользоваться биссектрисой угла:
1. Строят биссектрису угла;
2. Проводят прямую, параллельную одной из сторон угла и отстоящую от нее на расстоянии R;
3. Точка пересечения этой прямой с биссектрисой определяет положение центра скругления О1;
4. Пересечение перпендикуляров опущенных из центра скругления со сторонами определят положение точек сопряжения А и В;
5. Поводим дугу АВ из центра О1 радиусом R.

Внешнее сопряжение прямой линии с дугой

Сопряжение дуги окружности радиуса R с прямой, заданной отрезком АВ, дугой радиусом r выполняется в следующей последовательности:
1. Находим центр сопряжения — точку О1, как точку пересечения прямой параллельной АВ и отстоящей от нее на расстоянии r и дуги окружности радиуса R+ r, концентричной заданной;
2. Опускаем перпендикуляр из точки О1 на прямую АВ. Основание перпендикуляра — точка D — точка сопряжения;
3. Соединяем прямой центр окружности О с центром сопряжения О1, которая пересекая заданную окружность, определит положение второй точки сопряжения Е.

Внутреннее сопряжение прямой линии с дугой

Сопряжение дуги окружности радиуса R с прямой, заданной отрезком АВ, дугой радиусом r выполняется в следующей последовательности:
1. Находим центр сопряжения — точку О1, как точку пересечения прямой параллельной АВ и отстоящей от нее на расстоянии r и дуги окружности радиуса R- r, концентричной заданной;
2. Опускаем перпендикуляр из точки О1 на прямую АВ. Основание перпендикуляра — точка D — точка сопряжения;
3. Соединяем прямой центр окружности О с центром сопряжения О1, которая пересекая заданную окружность, определит положение второй точки сопряжения Е.

Внешнее сопряжение дуг

При внешнем сопряжении центры О₁ и О₂ сопрягаемых дуг радиусов R₁ и R₂ лежат вне сопрягающей дуги радиуса R.

Внешнее сопряжение дуг выполняется в следующей последовательности:

1. Находим центр сопряжения, точку О пересечения дуг окружностей с радиусами R₁+R и R₂+R соответственно концентричных окружностям с радиусами R₁ и R₂;

2. Соединяем прямыми центр сопряжения О с центрами окружностей О₁и О₂, которые пересекаясь с заданными окружностями определяют положение точек сопряжения А и В;

3. Строят сопряжение.

Внутреннее сопряжение дуг

При внутреннем сопряжении центры О₁ и О₂ сопрягаемых дуг радиусов R₁и R₂ лежат внутри сопрягающей дуги радиуса R.

Внутреннее сопряжение дуг выполняется в следующей последовательности:

1. Находим центр сопряжения, точку О пересечения дуг окружностей с радиусами R-R₁ и R-R₂ соответственно концентричных окружностям с радиусами R₁ и R₂;

2. Соединяем прямыми центр сопряжения О с центрами окружностей О₁и О₂, которые пересекаясь с заданными окружностями определяют положение точек сопряжения А и В;

3. Строят сопряжение.

Смешанное сопряжение

При смешанном сопряжении центр О2 одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R, а центр О1 другой сопрягаемой дуги вне ее.

Внутреннее сопряжение дуг выполняется в следующей последовательности:

1. Находим центр сопряжения, точку О пересечения дуг окружностей с радиусами R+R1 и R-R2 соответственно концентричных окружностям с радиусами R1 и R2;
2. Соединяем прямыми центр сопряжения О с центрами окружностей О1и О2, которые пересекаясь с заданными окружностями определяют положение точек сопряжения А и В;
3. Строят сопряжение.

Источник