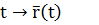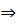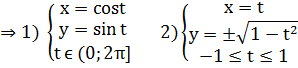Геометрический способ получения кривой

Параметризация кривой

Задания кривой с помощью радиус-вектора (векторно-параметрически) означает, что каждому числовому заданию параметра t мы ставим в соответствие вектор r=r(t). Если собрать все точки этих векторов в одну точку, то концы этих векторов опишут кривую, годограф вектор-функции. Таким образом между типовыми значениями параметра t и точками на кривой установлено взаимно-однозначное соответствие. Такое соответствие и называется параметризацией кривой.

Замечание. Параметризовать кривую можно не единственным образом, если параметр t = f(u), где f = f(u) – непрерывная монотонная (иногда возрастающая) функция, то мы получим новую параметризацию кривой с помощью вектор – функции r = r(t) = r(f(u)).

Пример. 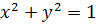(единичная окружность)

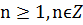
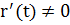
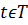
Определение. Будем называть кривую L – регулярной (n–раз дифференцируемой) без особых точек, если эта кривая допускает параметризацию с помощью параметра t такую, что вектор-функция r = r(t) n–раз дифференцируема ( ) и при всех значениях параметра . В частности рассматриваем кривые, класс гладкости которых n=1, 2 или 3.

Аналитические способы задания плоских (пространственных) кривых.

def. Криваяназывается плоской, если все ее точки принадлежат некоторой плоскости.

Способ задания	Кривая
Явный	y = f(x)
Неявный	F(x,y) =0 (*)
Параметрический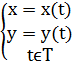
Векторно-параметрический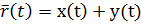

Замечание. Если между решением уравнения (*) и точками кривой 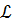существует взаимно-однозначное соответствие, то уравнение определяет кривую .

Способы аналитического задания (образования) кривых

1) Как линии пересечения данной поверхности и данной плоскости.

2) Как геометрическое место точек (ГМТ) обладающих данным свойством.

3) Как траектория точки, характер движения которой известен (….).

4) По способу сопряжения проективно соответствующих элементов.

5) Заданием ее дифференциальных свойств ( как положительное решение некоторого дифференциального уравнения).

6) В результате геометрического преобразования уже известной кривой.

7) Аналитический способ задания (в виде решения уравнения).

Пример. Указать, какие линии задаются уравнением в ПСК:

a) ,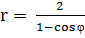

.

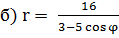
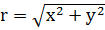
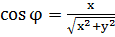
Способ 1. Используя зависимость и , переходим в ДПС и преобразовываем кривую к каноническому виду.

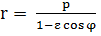
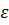
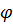
Способ 2. В общем виде уравнения кривой 2-го порядка равенство , где р – фокальный параметр, — эксцентриситет и — положительный угол.

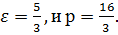
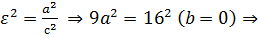
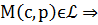
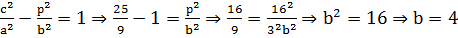
Тогда (из уравнения случай б)) Но отрезок. гипербола. .

Источник

Элементы дифференциальной геометрии. Естественная параметризация

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Наглядный геометрический объест — плоская кривая — приточных определениях приводит к нескольким различным, хотя и близким понятиям. Плоскую кривую можно понимать и как некоторое множество точек на плоскости и как множество точек плоскости вместе с очередностью их прохождения — ориентацией. Приведем два наиболее распространенных подхода к определению того, что представля ет собой плоская кривая. Пусть на плоскости введена прямоугольная декартова система координат Оху.

Определение 1 (неявный способ задания):

Плоской кривой называется множество 7 точек М плоскости, координаты х и у которых при подстановке в уравнение ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые. Способы задания. Естественная параметризация обращают его в тождество. Пример 1 Уравнение , задает окружность радиуса а с центром в точке 0(0,0) <рис. 1).

Другим распространенным способом задания плоской кривой является параметрический способ задания. Определение 2. Параметризованной плоской кривой называется множество 7 точек М плоскости, координаты г и у которых определяются соотношениями непрерывные на отрезке [а, 6] функции. Пример 2. — параметрические уравнения окружности радиуса а с центром в точке 0(0,0). При изменении параметра t от 0 до 2т соответствующая точка обегает окружность против часовой стрелки.

Данное определение допускает естественную физическую интерпретацию. Если воспринимать параметр t как время, то параметрически заданную кривую можно рассматривать как след движущейся точки М(х, у), координаты которой изменяются со временем по правилу (2). При этом вовсе не исключается случай, когда при своем движении переменная точка М в некоторый момент t* может вновь оказаться там, где ранее (в момент i, она уже находилась: (рис.2). Геометрически этоодна и та же точка.

Однако вследствие того, что в рассматриваемом процессе мы попадаем в нее дважды в разные моменты времени, это две разные точки кривой, задаваемой параметрическими уравнениями (2). Замечание. Строго говоря, определении I и 2 вводят в рассмотрение разные объекты. Поэтому для того, чтобы не впасть в заблуждение, нужно ясно представлять, в каком именно смысле рассматривается задаваемая кривая. Пусть кривая 7 задана параметрическими уравнениями называется начальной тонкой этой кривой, а точка ) — конечной тонкой кривой 7.

Кривая 7 называется замкнутой, если ее начальная и конечная точки совпадают (рис. 4).

— Рис. 4 Одно и то же м ножество точекн а плоскости можно задавать при помощи различных параметрических уравнений. Пример 3. Уравнения задают окружность радиуса а, обходимую в положительном направлении. Легко видеть, что, положив в формулах (3) 2хг3, мы приходим к соотношениям (4). Определение. Функция подчиненная условиям: а) Н<т) непрерывна на отрезке [а, /3]; h(r) строго возрастает на отрезке [се, >3]; в) область значения функции h(r) — отрезок [а, Ь], называется непрерывной заменой параметра кривой 7 (рис. 5). ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые.

Способы задания

Естественная параметризация Заменяя в формулах (2) параметр t на функцию Л(т), получаем уравнения — другую параметризацию кривой 7. Любую кривую можно параметризовать многими различными способами. Определение 3. Плоская кривая 7 называется п-гладкой относительно параметризации если функции ) принадлежит классу .

Если порядок п гладкости функций несуществен, то говорят просто о гладкой кривой. Пример 4. Кривая заданная уравнениями является 3-гладкой (рис. в а). Пример S. Кривая 7, заданная уравнениями является 2-гладкой. Однако множеств о точек на плоскости, описываемое этими уравнениями, имеет • точке О (при t ) особенность — излом (рис.вб). Это означает, что гладкость функций . задающих кривую, не обеспечивает плавного ее изменения.

Отметим, что производные этих функций при tодновременно обращаются а нуль. ТЪчка Мо гладкой кривой у, отвечающая значению t0 параметра, М0 в которой называется особой точкой этой кривой (относительно заданной параметризации). Точка Мо(*о) гладкой кривой 7, в которой называется обыкновенной, ншрегулярной, точкой этой кривой. Пример в. Все точки окружности (3) являются регулярными.

Пример 7. У кривой, задаваемой уравнениями (астроида) четыре особых точки (при t ж 0, | Последнее неравенство означает, что скорость кривой 7 относительно заданной параметризации не обращается в нуль ни в одной точке кривой. При изменении параметра t текущая точка M(t) перемещается порегулярной кривой 7, нигде не оста- навливаясь и не поворачивая вспять, поскольку скорость регулярной кривой ни при каких значениях параметра не обращается в нуль.

Возможно вам будут полезны данные страницы:

Пусть 7 — регулярная кривая, заданная параметрически. Обозначим через Мо точку кривой 7, отвечающую значению £о параметра, а через М — точку кривой 7, отвечающую значению t параметра из некоторой окрестности точки to (рис. 8, 9). Прямая М0Т называется касательной регулярной кривой 7 вточке Мо, если при (или, что то же, ) наименьший Д0 из углов между этой прямой и переменной прямой MqM стремится к нулю (рис. 9). Регулярная кривая имеет касательную в каждой своей точке.

Вектор скорости кривой в точке Мо коллинеарен ее ка- сательной в этой точке. Прямая, проходящая через точку Мо перпендикулярно касательной кривой 7 в этой точке, называется нормалью кривой вточке Мо. Замена параметра называется регулярной у если Л'(т во всех точках отрезка [а, /3]. В случае неявного задания (1) кривая 7 будет регулярной, если в каждой ее точке М(х, у) выполняется неравенство Точка Мо(жо> Уо) неявно заданной кривой 7 называется особой, если в этой точке Пример 8.

Кривая, заданная уравнением

(леммисюга Бернулт), имеет одну особую точку 0(0,0) — узел (рис.10). Различают несколько типов особых точек. Пусть М0(хо, уо) — особая точка кривой 7, Введем следующие обозначения возврата первого рода. Пример 12. (рис. 14). — точка возврата второго рода. Гладкая (тем более регулярная) кривая спрямляема. Длина кривой 7, заданной уравнениями (2), вычисляется по формуле Значение функции равно длине переменной дуги кривой7, заключенной между точками (рис. 15).

Функция на отрезке [а, 6) строго возрастает, Пример 11. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые. Способы задания. Естественная параметризация и является гладкой на отрезке [а, 6]. Кроме того, область значений функции s(t) совпадает с отрезком [0, 5]. Тем самым, длину дуги можно взять за новый, естественный (натуральный) параметр кривой.

Параметризация кривой, где в качестве параметра взята длина дуги з, называется естественной параметризацией. Если естественная параметризация кривой, то Поэтому естественно параметризованную кривую часто называют кривой с единичной скоростью. Пример 13. Параметризация окружности радиусе а является естественной:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник

Кривые Безье и Пикассо

Пабло Пикассо в своей студии на фоне картины «Кухня», фотография Херберта Листа.

Художник и простота

Одни из самых любимых мной работ Пабло Пикассо — это его линейные рисунки. Он изобразил на некоторых из них животных: сову, верблюда, бабочку и т.д. Эта работа под названием «Собака» висит на моей стене:

(Можете перейти к интерактивному демо, в которой мы воссоздали «Собаку» с помощью представленных в статье математических расчётов)

Эти рисунки чрезвычайно просты, но каким-то образом им удаётся глубоко тронуть зрителя. Они создают впечатление простоты композиции и реализации. Одно движение руки и подпись создают настоящий шедевр! Рисунок одновременно кажется и небрежной импровизацией, и точно подобранной увертюрой в симфонии изящества. На самом деле мы знаем, что процесс работы Пикассо был глубоким. Например, в 1945-1946 годах Пикассо создал серию из одиннадцати рисунков (литографий, если точнее), демонстрирующих его постепенный прогресс в визуализации быка. Первые были более-менее похожи на реалистичные, но в дальнейшем мы видим, как бык превращается в саму свою сущность, а последний рисунок состоит всего из десятка линий. В процессе развития серии рисунков мы видим быка, напоминающего некоторые из других работ Пикассо (номер 9 напоминает мне скульптуру в чикагском Daley Center Plaza). Здесь можно подробнее прочитать о серии литографий.

«Бык» Пикассо. Фотография сделана Джереми Куном в Институте искусств в Чикаго. Нажмите на изображение, чтобы увеличить его.

Я не буду притворяться опытным художником (я не смог бы нарисовать быка, даже если бы от этого зависела моя жизнь), зато я могу распознать математические аспекты его картин и написать чертовски хорошую программу. Есть один очевидный способ рассмотрения линейных рисунков в стиле Пикассо как математических объектов, и это конечно же кривые Безье. Давайте начнём с изучения теории кривых Безье, а потом напишем программу для их отрисовки. Используемая в ней математика не требует никаких дополнительных знаний, кроме основ алгебры и полиномов, и я постараюсь как можно меньше вдаваться в сложные подробности. Мы изучим очень простой алгоритм рисования кривых Безье, реализуем его на Javascript, а затем воссоздадим один из линейных рисунков Пикассо с помощью нескольких кривых Безье.

Кривые Безье и параметризация

Когда кто-нибудь просит вспомнить «кривые», большинство людей (возможно, отравленных преподаванием основ математики) или начинает трястись от страха, или рисует часть графика многочлена. Хотя это вполне правильные и уважаемые кривые, но они представляют лишь небольшую часть мира кривых. Особенно нас интересуют кривые, которые не являются частью графиков функций.

Например, лекало — это физический шаблон, используемый для (ручного) рисования плавных кривых. Просто соединяя рёбрами любую часть этих кривых, мы обычно не можем получить график функции. Очевидно, что нам нужна более общая идея о том, что же такое кривые. Проблема в том, что в разных областях математики под «кривой» подразумеваются различные понятия. Кривые, которые мы будем изучать, называемые «кривыми Безье» — это особый случай полиномиальных плоских кривых с одним параметром. Это звучит слишком сложно, но на самом деле это означает, что всю кривую можно задать двумя многочленами: одним для значений и вторым для значений . Оба многочлена имеют одну переменную, которую мы назовём ( определена на множестве вещественных чисел).

На примере всё должно стать понятнее. Давайте подберём два простых многочлена от , допустим, и . Если мы хотим найти точки на этой кривой, мы просто выбираем значения и подставляем их в оба уравнения. Например, подставив , мы получим точку на кривой. Располагая все такие значения на графике, мы получим кривую, которая точно не является графиком функции:

Но очевидно, что мы можем записать любую функцию с одной переменной в таком параметрическом виде: просто выберем и . Итак, они на самом деле являются более общими объектами, чем обычные функции (однако в этой статье мы будем работать только с многочленами).

Вкратце повторим: полиномиальная плоская кривая с одним параметром задаётся как пара многочленов от одной переменной . Иногда, когда нам нужно выразить всю систему одним уравнением, мы можем взять коэффициенты общих степеней и записать их как векторы и . Благодаря приведённому выше примеру мы можем переписать это как .

Здесь коэффициенты — это точки на плоскости (те же, что и векторы), и мы выделяем функцию жирным, чтобы подчеркнуть, что выходные данные являются точкой. Изучающие линейную алгебру могут понять, что пары многочленов формируют линейное пространство, и скомбинировать их как . Но для нас удобнее будет воспринимать точки как коэффициенты одного многочлена.

Мы также ограничим наше внимание рассмотрением однопараметрических плоских кривых, описываемых полиномом, для которых переменная допускается на интервале от нуля до единицы. Такое ограничение может показаться странным, но на самом деле так может быть записана любая конечная однопараметрическая плоская кривая, описываемая полиномом (мы не будем вдаваться в подробности того, как это реализуется). Ради краткости далее я буду называть однопараметрическую плоскую кривую, определяемую полиномом, у которой находится в интервале от нуля до единицы, просто «кривой».

С этими кривыми мы можем делать очень интересные вещи. Например для любых двух точек в плоскости мы можем описать прямую между ними как кривую: . И в самом деле, при значение точно равно , при точно равно , и уравнение является линейным полиномом при . Более того (если не вдаваться в подробности матанализа), линия проходит с «единичной скоростью» от до . Другими словами, мы можем воспринимать как описывающую движение частицы из по времени, и во время частица пройдёт путь на четверть, а во время пройдёт половину пути, и т.д. (Примером прямой, не имеющей единичную скорость, является, например .)

Для более общего случая давайте добавим третью точку . Мы можем описать путь, проходящий через в , и он «направляется» точкой , лежащей посередине. Эта идея «направляющей» точки немного абстрактна, но в отношении вычислений не более сложна. Вместо движения из одной точки в другую с постоянной скоростью, мы хотим двигаться из одной линии к другой с постоянной скоростью. То есть мы можем назвать две кривые, описывающие прямые из и кривыми и . Тогда кривая, «направляемая» точкой , может быть записана как кривая

Выполнив все эти умножения, мы получим формулу

С течением времени точка движется вдоль прямой между точками и , которые также движутся. Так мы получаем кривую, которая выглядит следующим образом

Этот скриншот взят из потрясающего демо консультанта по визуализации данных Джейсона Дейвиса. Он идеально демонстрирует математическую идею. В демо можно перетаскивать все три точки, чтобы посмотреть, как это влияет на конечную кривую. Стоит поиграть с ней хотя бы пять минут.

Вся идея кривых Безье заключается в обобщении этого принципа: имея список точек на плоскости, мы хотим описать кривую, которая проходит от первой до последней точки, и «направляется» между остальными точками. Кривая Безье является реализацией такой кривой (однопараметрической плоской кривой, определяемой полиномом), которая становится индуктивным продолжением описанного выше: мы движемся с единичной скоростью из кривой Безье, заданной первыми точками списка до кривой, заданной последними точками. В простейшем случае это отрезок прямой линии (или единственная точка, если угодно). С формальной точки зрения,

Определение: для заданного множества точек на плоскости мы рекурсивно определяем кривую Безье степени как

Мы назовём контрольными точками .

Хотя концепция перемещения с единичной скоростью между двумя кривыми Безье более низкого порядка является настоящей сутью дела (и позволяет нам подойти с к решению с вычислительной точки зрения), можно просто всё это перемножить (с помощью формулы биномиальных коэффициентов) и получить формулу в явном виде. Она будет следующей:

Например, кубическая кривая Безье с контрольными точками будет иметь уравнение

Кривые Безье более высокого порядка может быть достаточно сложно отобразить геометрически. Например, ниже показана кривая Безье пятой степени (с шестью контрольными точками).

Кривая Безье пятой степени, иллюстрация из Википедии.

Отрисованные дополнительные отрезки прямых демонстрируют рекурсивную природу кривой. Самые простые — зелёные точки, перемещающиеся между контрольными точками. Синие точки перемещаются по отрезкам прямых между зелёными точками, розовые перемещаются по отрезкам между синими, оранжевые — между розовыми, и, наконец, красная точка перемещается по отрезку прямой между оранжевыми точками.

Без рекурсивной структуры задачи (просто из наблюдения за кривой) было бы сложно понять, как можно всё это вычислить. Но как мы увидим, алгоритм отрисовки кривой Безье очень естественен.

Кривые Безье как данные и алгоритм де Кастельжо

Давайте выведем и реализуем алгоритм отрисовки кривой Безье на экране, воспользовавшись исключительно возможностью рисования прямых линий. Для простоты мы ограничимся рассмотрением только кривых Безье третьей степени (кубических). И в самом деле, любая кривая Безье по рекурсивному определению может быть записана как сочетание кубических кривых, и на практике кубические кривые обеспечивают баланс между эффективностью вычислений и выразительностью. Весь код в этом посте написан на Javascript и выложен на странице этого блога на Github.

Итак, кубическая кривая Безье представляется в программе списком из четырёх точек. Например,

В большинстве графических библиотек (в том числе в стандартной HTML5 canvas) существует графический примитив, способный выводить кривые Безье на основании списка из четырёх точек. Но предположим, что у нас нет такой функции. Предположим, что мы можем рисовать только прямые линии. Как же мы можем нарисовать аппроксимацию кривой Безье? Если такой алгоритм существует (а он есть, и мы убедимся в этом), то мы можем создать настолько точную аппроксимацию, что она будет визуально неотличима от истинной кривой Безье.

Важнейшее свойство кривых Безье, которое позволит нам создать такой алгоритм, заключается в следующем:

Любую кубическую кривую Безье от начала до конца можно разделить на две, которые вместе будут описывать ту же кривую, что и .

Давайте посмотрим, как же это сделать. Пусть будет кубической кривой Безье с контрольными точками , и допустим, что мы хотим разделить её ровно пополам. Мы заметим, что формула кривой при подстановке примет вид

Более того, наше рекурсивное определение даёт нам способ вычислить точку на основании кривых меньшей степени. Но когда вычисления выполняются при 1/2, их формулы достаточно просто записать. Изображение выглядит так:

Зелёные точки — это кривые первой степени, розовые точки — кривые второй степени, а синяя точка — это кубическая кривая. Мы заметим, что поскольку каждая из кривых вычисляется при , каждую из этих точек можно описать как среднюю точку уже известных нам точек. Поэтому , и т.д.

На самом деле, разделение на две нужные нам кривые точно задаётся этими точками. То есть половина кривой задаётся с контрольными точками , в то время как «правая» половина имеет контрольные точки .

Как мы можем быть уверены, что это точно те же кривые Безье? Ну, это просто полиномы. Мы можем проверить их на равенство с помощью запутанных алгебраических вычислений. Но стоит заметить, что поскольку проходит только полпути вдоль , то проверка их на равенство аналогична приравниванию с , поскольку изменяется в интервале от нуля до единицы, изменяется в интервале от нуля до половины. Аналогично, мы можем сравнить с .

Алгебраические вычисления очень запутаны, но вполне посильны. В доказательство привожу скринкаст того, как я выполняю вычисления, доказывающие идентичность двух кривых.

Теперь, когда мы всё проверили, у нас есть хороший алгоритм для разделения кубической кривой Безье (или любой кривой Безье) на две части. На Javascript он будет выглядеть так:

Здесь curve — это список из четырёх точек, как описано в начале этого раздела, а выходными данными является список двух кривых с правильными контрольными точками. Используемая функция midpoints достаточно проста, и для полноты мы тоже добавим её сюда:

Она просто получает на входе список точек и вычисляет их последовательные средние точки. То есть список из точек превращается в список из точек. Как мы видели, нам нужно вызывать эту функцию для вычисления сегментации кривой Безье степени .

Как я объяснил ранее, мы можем продолжать подразделять нашу кривую снова и снова, пока каждая из небольших частей не станет практически прямой. То есть наша функция для отрисовки кривой Безье будет следующей:

Если выразить словами, то поскольку наша кривая не «плоская», мы хотим рекурсивно подразделять и отрисовывать каждую часть. Если она плоская, то мы можем просто отрисовать три отрезка прямых кривой и логично считать, что это будет хорошей аппроксимацией. Используемая здесь переменная контекста представляет собой холст (canvas), на которой должна выполняться отрисовка; её нужно передавать фунции drawSegments , которая просто отрисовывает на холсте прямую линию.

Разумеется, это ставит перед нами очевидный вопрос: как мы можем определить, что кривая Безье плоская? Для этого есть множество способов. Можно вычислять углы отклонения (от прямой) в каждой внутренней контрольной точке и складывать их. Или можно вычислить объём образуемого четырёхугольника. Однако вычисление углов и объёмов обычно не так удобно: на расчёты углов тратится много времени, объёмы имеют проблемы со стабильностью, а стабильные алгоритмы не очень просты. Нам нужно измерение, для которого достаточно простой арифметики и, возможно, проверки нескольких логических условий.

Оказывается, что такое измерение существует. Его изначально приписывают Роджеру Уилкоксу, но оно достаточно просто выводится вручную.

В сущности, мы хотим измерить «плоскостность» кубической кривой Безье вычислением расстояния от настоящей кривой во время до того места, где кривая должна бы быть во время , если она является прямой.

Формально, имея заданную с контрольными точками , мы можем определить прямолинейную кубическую кривую Безье как колоссальную сумму

Здесь не происходит ничего волшебного. Мы просто задаём кривую Безье с контрольными точками . Нужно воспринимать их как точки, которые находятся на 0, 1/3, 2/3 и 1 доли пути от до на прямой линии.

Теперь мы зададим функцию , которая будет расстоянием между двумя кривыми в одно и то же время . Значение плоскостности — это максимум функции по всем значениям . Если значение плоскостности ниже определённого уровня допуска, то мы будем считать кривую плоской.

Добавив немного алгебры, мы можем упростить это выражение. Во-первых, значение , для которого расстояние максимально, аналогично тому, у которого максимален квадрат, поэтому мы можем избежать вычисления квадратного корня в конце и учитывать это при выборе допуска плоскостности.

Теперь давайте запишем разность как один полином. Во-первых, мы можем избавиться от троек в и записать полином как

и поэтому равно (при сложении коэффициентов подобных членов

Вынеся за скобки из обоих членов и обозначив , , получим

Поскольку максимумом произведения является произведение максимумов, мы можем ограничить вышеприведённую величину произведением двум максимумов. Причина этого в том, что мы сможем просто вычислить два максимума по отдельности. Вычислить максимум несложно и без разделения, но при таком способе нам потребуется меньше этапов вычислений в готовом алгоритме, а визуальный результат будет таким же хорошим.

Применив элементарные вычисления с единственной переменной, получим, что максимальное значение для оказывается равным . А норма вектора — это просто сумма квадратов его компонентов. Если и , то представленная выше норма равна

И заметьте: для любых вещественных чисел величина в точности является прямой линией из в , которая нам хорошо знакома. Максимум для всех от нуля до единицы очевидно будет равен максимуму конечных точек . Так что максимум нашей функции расстояния ограничен

И поэтому наше условие плоскостности заключается в том, чтобы это ограничение было меньше некоторого допуска. Мы можем безопасно разложить 1/16 на множители в это ограничение допуска, и этого будет достаточно для того, чтобы записать функцию.

Вот и она. Мы написали простую HTML-страницу, чтобы получить доступ к элементу canvas и несколько вспомогательных функций для отрисовки отрезков прямой, когда кривая достаточно плоская, и представили конечный результат в этом интерактивном демо (контрольные точки можно двигать).

Изображение, которое вы видиет на этой странице (ниже) — это моя визуализация «Собаки» Пикассо, нарисованная как последовательность кривых Безье. Думаю, что сходство вполне убедительное.

«Собака» Пикассо, собранная из последовательности девяти кривых Безье.

Хотя сам рисунок изобрели не мы (и потому не можем поставить под ним свою подпись), мы смогли представить его как последовательность кривых Безье. Можно только назвать их художественной работой. Здесь мы свели представление к одному файлу: первая строка — это размер холста, а каждая последующая строка представляет кубическую кривую Безье. Комментарии добавлены для лучшей читаемости.

«Собака», Джереми Кун, 2013 год.

Стандартизация кажется мне важной, поэтому мы определим новый тип файла «.bezier», который будет иметь показанный выше формат:

Здесь первые два целых числа определяют размер холста, первое (необязательное) целое число в каждой строке задаёт ширину линии, а curve имеет вид

Если int в начале строки отсутствует, то линии задаётся ширина в три пикселя.

В целом, файл .bezier может задавать кривую с произвольным количеством контрольных точек, однако представленный выше код не отрисовывает их в общем виде. В качестве упражнения попробуйте написать программу, которая получает на входе файл .bezier, а на выходе создаёт изображение рисунка. Для этого потребуется расширить представленный выше алгоритм, чтобы он мог рисовать произвольные кривые Безье, циклически производя вычисления средних точек и отслеживая те из них, которые оказываются конечным подразделением. Или же можно написать программу, получающую на входе файл .bezier только с кубическими кривыми Безье, а на выходе выдающую файл SVG рисунка (SVG поддерживает только кубические кривые Безье). То есть файл .bezier является упрощением (меньше возможностей) и расширением (кривые Безье произвольной степени) файла SVG.

Мы не так сильно углублялись в теорию кривых Безье, как могли бы. Если вы хотите изучить тему глубже (и с использованием матанализа), то см. этот длинный вводный курс. В нём содержится практически всё, что нужно знать о кривых Безье, а также представлены написанные на Processing интерактивные демо.

Искусство низкой сложности

У того, что мы сделали с «Собакой» Пикассо, есть некое философское значение. Ранее в этом блоге мы исследовали идею искусства низкой сложности, и здесь она полностью применима. Основная мысль заключается в том, что «красивое» искусство имеет описание малой длины; если более формально, то «сложность» объекта (представленного в тексте) — это длина самой короткой программы, дающей на выходе этот объект при отсутствии входных данных. Подробнее об этом можно прочитать в нашем введении в колмогоровскую сложность. Тот факт, что мы можем описать линейные рисунки Пикассо малым числом кривых Безье (и относительно короткой программой, дающей на выходе кривые Безье), должен быть глубоким заявлением о красоте самого искусства. Очевидно, что такой взгляд очень субъективен, но у него есть свои сторонники.

Сегодня существует интерес к генерируемому компьютером искусству. Например, в этих недавних соревнованиях по программированию (статья на нидерландском) участникам дали задание сгенерировать рисунок, напоминающий работу Пита Мондриана. Идея заключалась в том, что чем элегантнее алгоритм, тем выше будет его оценка. Для генерации работ Мондриана победитель использовал хэши MD5, и есть ещё множество других впечатляющих примеров (по ссылке выше представлена галерея готовых работ).

В предыдущем посте об искусстве низкой сложности мы исследовали возможность представления всех изображений в системе координат, в которой используются окружности с закрашенным внутренним пространством. Но очевидно, что в такой системе координат нельзя представить «Собаку» с очень низкой сложностью. Похоже, что кривые Безье — это гораздо более естественные системы координат. Небольшие усовершенствования, включающие в себя длину линий и небольшие искажения, не влияют на конечную сложность. Кубическую кривую Безье можно описать любым множество из четырёх точек, а для более «запутанных» описаний (с повышенной сложностью) требуется большее количество точек. Кривые Безье можно произвольно масштабировать, и это не изменит значительно сложность кривой (несмотря на то, что масштабирование на многие порядки величины добавит увеличение сложности с логарифмическим множителем, оно довольно мало). Кривые с большой шириной линий немного сложнее, чем с малой шириной, а для представления множества мелких острых изгибов требуется больше кривых, чем для длинных и плавных дуг.

Недостатком является сложность представления в виде кривой Безье окружности. На самом деле, точно это сделать невозможно. Несмотря на простоту этого объекта (он даже задаётся как единственный многочлен, хотя и с двумя переменными), лучшее, что можно с ним сделать — аппроксимировать его. То же относится и к эллипсам. На самом деле есть способы обхода этой проблемы (концепция рациональных кривых Безье, которые являются частными многочленов), но они добавляют в алгоритм отрисовки неотъемлемую сложность, а аппроксимации с использованием обычных кривых Безье выглядят достаточно хорошо.

Итак, мы определим сложность рисунка как количество битов в виде файла .bezier (комментарии при вычислениях не учитываются).

Настоящей наградой, которую мы ещё исследуем, будет нахождение способа автоматической генерации искусства. То есть реализации одной из двух возможностей:

1. Задав что-то вроде случайного начального числа (seed), написать программу, создающую псевдослучайный линейный рисунок.
2. Задав рисунок, создать изображение .bezier, точно воспроизводящее рисунок как линейный рисунок.

Мы попробуем исследовать эти возможности в последующем посте. Для этого могут потребоваться какие-нибудь алгоритмы локального поиска, генетические алгоритмы или другие способы.

Источник