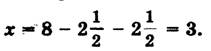Геометрические способы решения квадратных уравнений пифагора

Геометрические способы решения квадратных уравнений

Скачать
презентацию Пребудет вечной истина, как скоро Ее познает слабый человек И ныне >>

Геометрические способы решения квадратных уравнений.

Слайд 11 из презентации «Теорема Пифагора 8 класс». Размер архива с презентацией 382 КБ.

Геометрия 8 класс

«Таблицы по геометрии» — Многоугольники Параллелограмм и трапеция Прямоугольник, ромб, квадрат Площадь многоугольника Площадь треугольника, параллелограмма и трапеции Теорема Пифагора Подобные треугольники Признаки подобия треугольников Соотношения между сторонами и углами прямоугольного треугольника Взаимное расположение прямой и окружности. Таблицы. Касательная к окружности Центральные и вписанные углы Вписанная и описанная окружность Понятие вектора Сложение и вычитание векторов. Содержание:

«Урок Площадь трапеции» — Подсчитывают количество полученных баллов в данном задании. Решение поставленной задачи. Поочередно рассказывают все о трапеции: определение, виды, свойства равнобедренной трапеции. Деятельность учителя: Как можно выразить площадь трапеции ? Самостоятельная работа (Задания для самоконтроля оцениваются в баллах.). В прямоугольной трапеции основания 5см. и 17см., а меньшая боковая сторона 10см. Вариант 1 (3 балла) Основания трапеции m= 6см. и n= 8см., высота трапеции x=2см. Вариант 2. Какие свойства прямоугольного треугольника вы использовали при решении задач ?

«Четырехугольники» — Прямоугольник. Выбрать капитана. Ответы к кроссворду. Геометрия 8 класс. Защита презентаций. Четырехугольники. МОУ «Могочинская СОШ». Параллелограмм. Разминка! Кроссворд. Квадрат. Правильные ответы. Другие. Четырехугольники: Цели урока:

«Площади фигур» — А=1. Площадь квадрата со стороной 1 равна 1. А1. Площадь. Отношения площадей. С. Теорема. Учитель математики МОУ лицея №18 И.В.Дымова. D. Второе свойство: SABCDEF=SA1B1C1D1E1F1. Первое свойство: Презентация уроков по геометрии 8 класс по главе учебника. Е. Разрезания и складывания. Работу выполняла ученица 11«4» класса Степанова Аня.

«8 класс Четырехугольники» — Вариант 1. Точки, из которых выходят стороны четырёхугольников. Этапы урока. Цели урока. Подготовила Калачева Н.Н. учитель математики ГОУ СОШ № 851. Четырехугольники. Разминка. Тест по теории. Геометрия 8 класс.

«Теорема Пифагора 8 класс» — 10 см. Высота. Деление чисел на четные и нечетные, простые и составные. Теорема о сумме внутренних углов треугольника. Мыслитель Философ Математик. ФИГУРЫ. 3. c. Фигура, образованная двумя лучами, исходящими из одной точки. Угол. Формулировка Пифагора. Открытия пифагорийцев в математике. Геометрические способы решения квадратных уравнений.

Всего в теме «Геометрия 8 класс» 69 презентаций

Источник

Теорема Пифагора

О чем эта статья:

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

• a = √c 2 − b 2
• b = √c 2 − a 2
• c = √a 2 + b 2

Для фигуры со сторонами a, b и c, где c самая длинная сторона действуют следующие правила:

• если c 2 2 + b 2 , значит угол, обращенный к стороне c, является острым.
• если c 2 = a 2 + b 2 , значит угол, обращенный к стороне c, является прямым.
• если c 2 > a 2 +b 2 , значит угол, обращенный к стороне c, является тупым.

Записывайтесь на обучение по математике для учеников с 1 по 11 классы!

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a 2 + b 2 = c 2 .

Пошаговое доказательство:

• Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
• Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

• Также прямоугольная фигура ∆CBH подобна ∆ABC:

• Введем новые обозначения: BC = a, AC = b, AB = c.

• Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

• Значит a 2 = c * HB, b 2 = c * AH.
• Сложим полученные равенства:

a 2 + b 2 = c * HB + c * AH

a 2 + b 2 = c * (HB + AH)

a 2 + b 2 = c * AB

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такая фигура является прямоугольной.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

• Построим прямой угол с вершиной в точке C₁.
• Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

• Проведём отрезок A₁B₁.
• Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

• В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
• Таким образом получится:

• Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

1. C₁A₁ = CA и C₁B₁ = CB по результату построения,
2. A₁B₁ = AB по доказанному результату.

• Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
• Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 10 см. Какое значение у гипотенузы?

значит c 2 = a 2 + b 2 = 6 2 + 10 2 = 36 + 100 = 136

Задание 2. Является ли фигура со сторонами 8 см, 9 см и 11 см прямоугольным треугольником?

• Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

Ответ: треугольник не является прямоугольным.

Источник

СПОСОБ: Геометрический способ решения квадратных уравнений

10. СПОСОБ: Геометрический способ решения квадратных уравнений.

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.

1) Решим уравнение х 2 + 10х = 39.

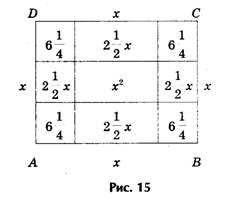
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.15).

Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25), т.е. S = х 2 + 10х + 25. Заменяя

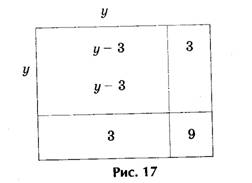
х 2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим

2) А вот, например, как древние греки решали уравнение у 2 + 6у — 16 = 0.

Решение представлено на рис. 16, где

у 2 + 6у = 16, или у 2 + 6у + 9 = 16 + 9.

Решение. Выражения у 2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у 2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у₁ = 2, у₂ = — 8 (рис.16).

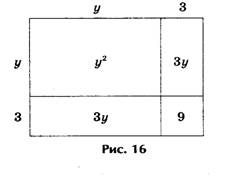
3) Решить геометрически уравнение у 2 — 6у — 16 = 0.

Преобразуя уравнение, получаем

На рис. 17 находим «изображения» выражения у 2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у 2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у 2 — 6у равным ему числом 16,

получаем: (у — 3) 2 = 16 + 9, т.е. у — 3 = ± √25, или у — 3 = ± 5, где у₁ = 8 и у₂ = — 2.

Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств.

Однако, значение квадратных уравнений заключается не только в изяществе и краткости решения задач, хотя и это весьма существенно. Не менее важно и то, что в результате применения квадратных уравнений при решении задач не редко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.

Хочется отметить и то, что излагаемая тема в этой работе еще мало изучена вообще, просто ею не занимаются, поэтому она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней.

Здесь я остановилась на вопросе решения квадратных уравнений, а что,

если существуют и другие способы их решения?! Опять находить красивые закономерности, какие-то факты, уточнения, делать обобщения, открывать все новое и новое. Но это вопросы уже следующих работ.

Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в развитии математики. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза. Эти знания могут пригодиться нам на протяжении всей жизни.

Так как эти методы решения квадратных уравнений просты в применении, то они, безусловно, должно заинтересовать увлекающихся математикой учеников. Моя работа дает возможность по-другому посмотреть на те задачи, которые ставит перед нами математика.

1. Алимов Ш.А., Ильин В.А. и др. Алгебра, 6-8. Пробный учебник для 6-8 классовой средней школы. — М., Просвещение, 1981.

2. Брадис В.М. Четырехзначные математические таблицы для средней школы.Изд. 57-е. — М., Просвещение, 1990. С. 83.

3. Кружепов А.К., Рубанов А.Т. Задачник по алгебре и элементарным функциям. Учебное пособие для средних специальных учебных заведений. — М., высшая школа, 1969.

4. Окунев А.К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. — М., Просвещение, 1972.

5. Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. — М., Квант, № 4/72. С. 34.

6. Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. — 4-е, дополн. — М., Высшая школа, 1973.

7. Худобин А.И. Сборник задач по алгебре и элементарным функциям. Пособие для учителя. Изд. 2-е. — М., Просвещение, 1970.

Источник

ГЕОМЕТРИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНОГО УРАВНЕНИЯ.

Описание презентации по отдельным слайдам:

Геометрическое решение квадратного уравнения Автор: Иванова Любовь Алексеевна

Цель: Научить учащихся владению основными способами решения квадратного уравнения Задачи: Изучить историю развития квадратных уравнений. Раскрыть геометрический способ решения квадратных уравнений.

Актуальность работы Квадратные уравнения используются как в учебном процессе, так и для олимпиад самого высокого уровня, а также при решении прикладных задач человеческой жизнедеятельности. Способность ученика подходить к решению уравнений с различных ракурсов, и при этом выбирать наиболее рациональный способ решения, повышает его конкурентоспособность и успешную самореализацию. Квадратные уравнения – «золото» Алгебры.

– это фундамент, на котором покоится величественное здание алгебры. Умение решать квадратные уравнения не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям. Большинство жизненных задач сводится к решению различных видов квадратных уравнений. Квадратное уравнение

История возникновения и развития квадратных уравнений

Кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет. Г.В. Лейбниц

решали квадратные уравнения. В древние времена математики ориентировались на человека, его нужды, заботы, возможности. Необходимо было вычислять площади земельных участков, производить расчеты при постройке военных сооружений. В Вавилоне 2 тысячи лет до нашей эры

В VIII столетии до нашей эры в Индии математик Баудхаяма впервые использовал запись квадратных уравнений в виде: и привел методы решения квадратных уравнений

Индийский астроном Ариабхатта

Индийский ученый Брахмагупта (VII век)

Диофант Александрийский (III в.)

«Книга абака» итальянского математика Леонардо Фибоначчи 1201 году

В XVII веке Жирар Декарт систематизировал все теории о квадратных уравнениях.

Геометрический способ решения квадратного уравнения

Пример 1. х2+ 10х -39 = 0 → х2 + 10х = 39 Решение: На сторонах квадрата с ребром х строим прямоугольники 1*х, полученную фигуру дополняем до квадрата ABCD. Площадь квадрата ABCD состоит из площади первоначального квадрата х; площадей десяти прямоугольников 10х и площади квадрата 52 = 25; АВ = х + 5; (х + 5)2 = х2 + 10х + 25 = 39; (х 5)2 = 39 + 25 = 64; х + 5 = ± ± 8; Ответ: х1 = 3; х2 = -13

Пример 2.Решите квадратное уравнение х2 + 6х + 5 = 0 Решение: х2 + 6х = -5; АВ = х + 3; SABCD = (х + 3)2; (х + 3)2 = х2 + 6х = 32; (х + 3)2 = 4; х + 3 = ±2; Ответ: х1 = -1; х2 = -5

Пример 3. Решите квадратное уравнение геометрически 4х2 + 8х – 5 = 0 Решение: 4х2 + 8х = 5; Разделим уравнение на четыре, получим приведенное квадратное уравнение х2 + 2х = ; которое решаем аналогично решениям примеров 1 и 2; х +1 = ± = Ответ: х1 = х2 = — 1

«Опыт научного прошлого не должен быть потерян для будущих поколений, всё развивается по спирали. Человек родился быть господином, повелителем, царем природы. Но мудрость, с которой он должен править с наследственного своего престола, не дана ему от рождения: она приобретается учением». Николай Иванович Лобачевский.

«Торопись, ведь они проходят, Ты у времени в гостях. Не рассчитывай на помощь, Помни: всё в твоих руках!» Юстас Палецкис

«Так, дерзай! Пусть славы эхо о твоих гремит успехах. Станешь ты, хоть скромен вид, знаменитей чем Евклид!» Льюис Керрол

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 821 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 290 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 605 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-304446

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

В России выбрали топ-10 вузов по работе со СМИ и контентом

Время чтения: 3 минуты

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Руководители управлений образования ДФО пройдут переобучение в Москве

Время чтения: 1 минута

Шойгу предложил включить географию в число вступительных экзаменов в вузы

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник