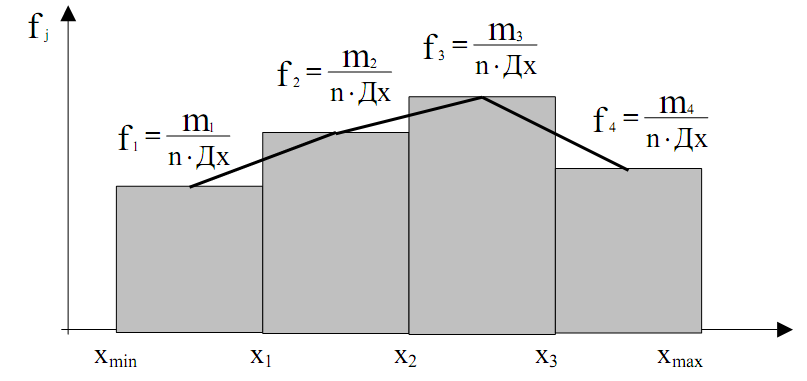
- Графический метод определения оценок параметров распределения
- Географический способ оценки закона распределения
- Геометрический закон распределения
- Геометрический закон распределения, функции его параметров на основе метода достаточных статистик. Интервальная и асимптотически оптимальная оценка неизвестных параметров геометрического закона распределения. Алгоритм проверки статистической гипотезы.
- Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
- Подобные документы
Графический метод определения оценок параметров распределения
Оценка параметров распределения производится по опытным данным. По ним же определяется, какому закону распределения соответствуют эти данные.
Можно было бы поступить следующим образом: нанести на график F(t) в прямоугольных координатах с равномерными шкалами значения этих величин, полученные из наблюдений, соединить точки F(t) плавной кривой и определить визуально, какому распределению это соответствует, сравнив с известными графиками. Однако кривые F(t) для разных законов распределения в ряде случаев похожи друг на друга и при таком методе может быть допущена грубая ошибка.
Оказывается, что путем несложных преобразований функцию F(t)можно в той же системе координат с неравномерными шкалами представить в виде прямой линии. В этом случае визуальное сравнение эмпирических данных с предполагаемым теоретическим значением может быть сделано с достаточной для практики точностью. Прямоугольная координатная сетка с измененным масштабом по осям носит название вероятностной сетки или вероятностной бумаги.
Для определения вида закона распределения случайной величины удобно представить данные наблюдений в графическом виде. Для графического представления данных наблюдения используется специальный график – гистограмма (рис. 16).
Рис. 16. Гистограмма и полигон распределения
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Географический способ оценки закона распределения
1. Статистические гипотезы. Основные понятия.
2. Гипотезы о законе распределения.
3. Гипотезы о числовом значении генерального среднего и дисперсии.
1. Статистические гипотезы. Основные понятия.
Статистическая гипотеза — это утверждение о виде неизвестного распределения или параметрах известного распределения. Статистические гипотезы проверяются по результатам выборки статистическими методами в ходе эксперимента (эмпирическим путем) с помощью статистических критериев.
В тех случаях, когда известен закон, но неизвестны значения его параметров (дисперсия или математическое ожидание) в конкретной ситуации, статистическую гипотезу называют параметрической.
Например, предположение об ожидаемом среднем доходе по акциям или разбросе дохода являются параметрическими гипотезами.
Когда закон распределения генеральной совокупности не известен, но есть основания предположить, каков его конкретный вид, выдвигаемые гипотезы о виде его распределения называются непараметрическими.
Например, можно выдвинуть гипотезу, что число дневных продаж в магазине или доход населения подчинены нормальному закону распределения.
По содержанию статистические гипотезы можно классифицировать:
1. Гипотезы о типе вероятностного закона распределения случайной величины, характеризующего явление или процесс.
2. Гипотезы об однородности двух или более обрабатываемых выборок. Изучаемое свойство исследуется с помощью двух или более генеральных совокупностей. Гипотеза в этом случае может заключаться в следующем: исследуемые выборочные характеристики различаются между собой статистически значимо или нет.
3. Гипотезы о свойствах числовых значений параметров исследуемой генеральной совокупности. Больше ли значения параметров некоторого заданного номинала или меньше и т.д.
4. Гипотезы о вероятностной зависимости двух или более признаков, характеризующих различные свойства рассматриваемого явления или процесса. При этом определяется характер этой зависимости.
Гипотезы бывают простые (содержащие одно предположение) и сложные (содержащие несколько предположений).
Выдвинутую гипотезу называют основной или нулевой и обозначают H0 . Противоречащую ей гипотезу называют альтернативной или конкурирующей и обозначают H1.
Под статистическим критерием понимают однозначно определенное правило, устанавливающее условие, при котором проверяемая гипотеза отвергается либо не отвергается.
Увеличение числа заболевших некоторым заболеванием дает возможность выдвинуть гипотезу о наличии эпидемии. Для сравнения доли заболевших в обычных и экстремальных условиях используются статистические данные, на основании которых делается вывод о том, является ли данное массовое заболевание эпидемией. Предполагается, что существует некоторый критерий- уровень доли заболевших, критический для этого заболевания, который устанавливается по ранее имевшимся случаям.
Различают три вида критериев:
1. Параметрические критерии — критерии значимости, которые служат для проверки гипотез о параметрах распределения генеральной совокупности при известном виде распределения.
2. Критерии согласия — позволяют проверить гипотезы о соответствии распределений генеральной совокупности известной теоретической модели.
3. Непараметрические критерии — используются в гипотезах, когда не требуется знаний о конкретном виде распределения.
Проверка параметрических гипотез проводится на основе критериев значимости., а непараметрических- критериев согласия.
Задача проверки статистических гипотез сводится к исследованию генеральной совокупности по выборке. Множество возможных значений элементов выборки может быть разделено на два непересекающихся подмножества- критическую область и область принятия гипотезы.
Областью принятия гипотезы или областью допустимых значений Iдоп называют совокупность значений критерия, при которых эту гипотезу принимают.
Критической областью Iкр называют множество значений критерия, при котором гипотезу отвергают.
Наблюдаемые значения критерия (статистика) Kнабл называют такое значение критерия, которое находится по данным выборки.
Границы критической области , отделяющие ее от области принятия гипотезы, называют критическими точками и обозначают Kкр.
Для определения критической области задается уровень значимости — некая малая вероятность попадания критерия в критическую область.
Уровень значимости — вероятность принятия конкурирующей гипотезы, тогда как справедлива основная.
С помощью уровня значимости определяются границы критической области.
Основной принцип проверки статистических гипотез состоит в следующем: если наблюдаемое значение статистики критерия попадает (не попадает) в критическую область, то гипотеза H0 отвергается (принимается), а гипотеза H1 принимается (отвергается) в качестве одного из возможных решений с формулировкой «гипотеза H0 противоречит (не противоречит) выборочным данным на уровне значимости ».
В зависимости от содержания альтернативной гипотезы осуществляется выбор критической области: левосторонней, правосторонней, двусторонней. Если смысл исследования заключается в доказательстве конкретного изменения наблюдаемого параметра (его уменьшения или увеличения), то говорят об односторонней критической области. Если смысл исследования- выявить различия в изучаемых параметрах, но характер их отклонения от контрольных (или теоретических) не известен, то говорят о двусторонней критической области.
Однако, принятие той или иной гипотезы не дает оснований утверждать, что она верна. Результат проверки статистической гипотезы лишь устанавливают на определенном уровне значимости ее соответствие (несоответствие) результатам эксперимента.
При проверке статистических гипотез возможны следующие ошибки:
1. Отвергнута правильная H0, а принята неправильная гипотеза H1 — ошибка первого рода.
2. Отвергнута правильная альтернативная гипотеза H1 и принята неправильная нулевая гипотеза H0 — ошибка второго рода.
Заметим, что уровень значимости — есть вероятность ошибки первого рода. Ошибка первого рода называется -риском . Обычно они задаются некоторыми конкретными значениями: 0,05; 0,01; 0,005; 0,001. Ошибки второго рода называются -риском , а вероятность ее допустить обозначается (вероятность того, что принята гипотеза H0 , когда на самом деле справедлива альтернативная гипотеза H1 .
Можно доказать, что с уменьшением ошибок первого рода одновременно увеличиваются ошибки второго рода и наоборот. Поэтому, на практике пытаются подбирать значения параметров и опытным путем в целях минимизации суммарного эффекта от возможных ошибок. При принятии управленческих решений для одновременного уменьшения ошибок первого и второго рода самым действенным средством является увеличение объема выборки, что согласуется с законом больших чисел.
На бытовом уровне ошибки второго рода могут иметь более трагические последствия, чем ошибки первого рода.
2. Гипотеза о законе распределения. Критерий согласия Пирсона ( X 2 -критерий).
Критериями согласия называют критерии, в которых гипотеза определяет закон распределения либо полностью, либо с точностью до небольшого числа параметров.
Причины расхождения результатов эксперимента и теоретических характеристик могут быть вызваны малым объемом выборки, неудачным способом группировки наблюдений, ошибками в выборе гипотезы о виде распределения генеральной совокупности и др.
Рассмотрим универсальный критерий согласия Пирсона. Проверка гипотезы о том, что эмпирическая частота мало отличается от соответствующей теоретической частоты, осуществляется с помощью величины X 2 — меры расхождения между ними.
Для произвольной выборки, когда распределение непрерывно или число различных вариант велико, все пространство наблюдаемых вариант делят на конечное число непересекающихся областей, в каждой из которых подсчитывают наблюдаемую частоту и теоретическую вероятность.
Для применения критерия согласия Пирсона необходимо:
1. Вычислить значение статистики по формуле: , где pi –вероятность принятия значения xi, ni. — эмпирическая частота для соответствующего xi. n — объем выборки. s — число вариант выборки.
2. По соответствующей таблице распределения Пирсона найти критическое значение , где k = s – r – 1 – число степеней свободы, s — число различных вариант или интервалов группировки, r — число неизвестных параметров предполагаемого теоретического распределения, — выбранный уровень значимости. Это значит, что строится правосторонний интервал.
3. Если , то основная гипотеза отвергается, в противном случае- принимается, т.е. чем больше отклонение, тем меньше согласованы теоретическое и эмпирическое распределение. Поэтому принято использовать только правостороннюю критическую область.
Источник
Геометрический закон распределения
Геометрический закон распределения, функции его параметров на основе метода достаточных статистик. Интервальная и асимптотически оптимальная оценка неизвестных параметров геометрического закона распределения. Алгоритм проверки статистической гипотезы.
| Рубрика | Математика |
| Вид | курсовая работа |
| Язык | русский |
| Дата добавления | 07.12.2009 |
| Размер файла | 410,1 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
1. Описание геометрического закона распределения 4
2. Оптимальные оценки параметров закона геометрического распределения и функции этих параметров на основе метода достаточных статистик 9
3. Асимптотически оптимальная оценка для неизвестных параметров закона распределения 10
4. Интервальная оценка математического ожидания геометрического закона распределения 11
5. Алгоритм проверки статистической гипотезы 12
Одним из важнейших понятий математической статистики является понятие случайной величины.
Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно — заранее неизвестно).
Случайная величина называется дискретной, если множество ее значений конечное, или бесконечное, но счетное.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайно величины и соответствующими им вероятностями.
Закон распределения дискретной случайной величины дает исчерпывающую информацию о ней, так как позволяет вычислить вероятности любых событий, связанных со случайной величиной.
Основными законами распределения дискретных случайных величин являются:
биномиальный закон распределения;
закон распределения Пуассона;
В данной работе рассматривается геометрический закон распределения случайной величины.
1. Описание геометрического закона распределения
Дискретная случайная величина Х=m имеет геометрическое распределение, если она принимает значения 1, 2, …, m, … (бесконечное, но счетное множество значений) с вероятностями
Ряд геометрического распределения случайной величины имеет вид:
Нетрудно видеть, что вероятности pi образуют геометрическую прогрессию с первым членом p и знаменателем q (отсюда название «геометрическое распределение»). Впервые термин геометрическое распределение был использован в работе Феллера (Feller, 1950).
Определение геометрического ряда распределения корректно, так как сумма ряда:
(так как есть сумма геометрического ряда при ).
Случайная величина Х = m, имеющая геометрическое распределение, представляет собой число m испытаний, проведенных по схеме Бернулли, с вероятностью р наступления события в каждом испытании до первого положительного исхода.
Так, например, число вызовов радистом корреспондента до тех пор, пока вызов не будет принят, есть случайная величина, имеющая геометрическое распределение,
График функции вероятности представлен на рис.1.
Рис.1. Функция вероятности геометрического распределения случайной величины
Описание геометрического закона распределения с помощью функции вероятности не является единственным, а главное не универсально. Для описания закона распределения случайной величины Х возможен и другой подход: рассматривать не вероятности событий Х=х для разных х (как это имеет место в ряде распределения), а вероятности события Х 1 геометрическое распределение Geom(1 / ?) является одним из распределений с максимальной информационной энтропией.
Если независимы и , то
Геометрическое распределение бесконечно делимо.
то есть количество прошлых «неудач» не влияет на количество будущих «неудач».
Геометрическое распределение — это единственное дискретное распределение со свойством отсутствия памяти.
Геометрическое распределение является частным случаем отрицательного биномиального распределения: .
Если независимы и , то
Пусть игральная кость вбрасывается до выпадания первой «шестёрки». Тогда вероятность, что нам потребуется не больше трёх вбросов равна:
Ожидаемое число бросков равно:
2. Оптимальные оценки параметров закона геометрического распределения и функции этих параметров на основе метода достаточных статистик
Геометрический закон распределения задается параметром р (вероятность «успеха»). Известно, что математическое ожидание случайной величины Х, распределенной по геометрическому закону распределения, равно ожидание
Следовательно, оценка параметра р геометрического закона распределения равна
3. Асимптотически оптимальная оценка для неизвестных параметров закона распределения
Сформулируем задачу оценки параметров в общем виде. Пусть распределение признака Х — генеральной совокупности — задается функцией вероятностей , которая содержит неизвестный параметр p.
Для вычисления параметра р исследовать все элементы генеральной совокупности не представляется возможным. Поэтому о параметре — вероятности р — пытаются судить по выборке, состоящей из значений х1, х2, х3, …, хn. Эти значения можно рассматривать как частные значения n независимых случайных величин Х1, Х2, …, Хn, каждая из которых имеет тот же закон распределения, что и сама случайная величина Х.
Оценкой параметра называют всякую функцию результатов наблюдений над случайной величиной Х (иначе статистику), с помощью которой судят о значении параметра.
Оценка является случайной величиной, зависящей от закона распределения случайной величины Х и числа n.
О качестве оценки следует судить не по индивидуальным ее значениям, а лишь по распределению ее значений в большей сети испытаний, т.е. по выборочному распределению оценки.
В качестве статистических оценок параметров генеральной совокупности желательно использовать оценки, удовлетворяющие одновременно требованиям несмещенности, состоятельности и эффективности.
В случае геометрического закона распределения для нахождения единственного параметра р достаточно приравнять теоретический эмпирический начальные моменты первого порядка — математическое ожидание случайной величины Х. Установлено, что для случайно величины, распределенной по геометрическому закону распределения, математическое ожидание
Следовательно, оценка параметра р геометрического закона распределения равна
4. Интервальная оценка математического ожидания геометрического закона распределения
Интервальной оценкой параметра р называется числовой интервал, который с заданной вероятностью покрывает неизвестное значение параметра р.
Доверительный интервал для параметра р геометрического закона распределения (вероятность р) имеет вид:
, — заданная доверительная вероятность,
n — объем выборки.
5. Алгоритм проверки статистической гипотезы
Сформулируем гипотезу Н0:
Р — параметр исследуемого распределения,
В качестве альтернативной гипотезы принимается одна из гипотез Н0:
Рассчитывается соответствующий критерий проверки гипотезы:
Определяется критическое значение статистики на заданном уровне значимости по соответствующим таблицам, исходя из соотношения:
Критерия отклонения гипотезы Н0 представлен в таблице.
Критерий отклонения гипотезы
Геометрическое распределение описывает время, протекающее до наступления определенного числа неудач.
Частным случаем распределения Паскаля является геометрическое распределение, получаемое при с=1.
Экспоненциальное распределение для непрерывного случайного аналогично геометрическому для дискретного случая. Если в геометрическом распределении случайная величина представляет число испытаний до первого отказа, то в экспоненциальном в непрерывном случае, соответствующим аналогом будет промежуток до первого отказа.
Геометрический закон распределения случайной величины широко используется при решении различных задач.
1. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. -М.: ЮНИТИ-ДАНА, 2003.
2. Практикум по статистике: Учеб. пособие для вузов./под ред. В.М. Симчеры. — М.: Финстатинформ, 1999.
3. Статистика: учебник / под ред. В.С. Мхитаряна. — М.: Экономистъ, 2005.
Подобные документы
Оценивание параметров закона распределения случайной величины. Точечная и интервальная оценки параметров распределения. Проверка статистической гипотезы о виде закона распределения, нахождение параметров системы. График оценки плотности вероятности.
курсовая работа [570,4 K], добавлен 28.09.2014
Задачи математической статистики. Распределение случайной величины на основе опытных данных. Эмпирическая функция распределения. Статистические оценки параметров распределения. Нормальный закон распределения случайной величины, проверка гипотезы.
курсовая работа [57,0 K], добавлен 13.10.2009
Изучение сути и выдвижение предположения о законе распределения вероятности экспериментальных данных. Понятие и оценка асимметрии. Принятие решения о виде закона распределения вероятности результата. Переход от случайного значения к неслучайной величине.
курсовая работа [126,0 K], добавлен 27.04.2013
Проверка выполнимости теоремы Бернулли на примере вероятности прохождения тока по цепи. Моделирование дискретной случайной величины, имеющей закон распределения Пуассона. Подтверждение гипотезы данного закона распределения с помощью критерия Колмогорова.
курсовая работа [134,2 K], добавлен 31.05.2010
Числовые характеристики непрерывных величин. Точечные оценки параметров распределения. Статистическая проверка гипотез. Сравнение средних известной и неизвестной точности измерений. Критерий Хи-квадрат для проверки гипотезы о виде распределения.
курсовая работа [79,0 K], добавлен 23.01.2012
Определение математического ожидания и дисперсии параметров распределения Гаусса. Расчет функции распределения случайной величины Х, замена переменной. Значения функций Лапласа и Пуассона, их графики. Правило трех сигм, пример решения данной задачи.
презентация [131,8 K], добавлен 01.11.2013
Закон и свойства нормального распределения случайной величины. На основе критерия согласия Пирсона построение гистограммы, статистической функции и теоретической кривой и определение согласованности теоретического и статистического распределения.
курсовая работа [894,5 K], добавлен 30.10.2013
Источник