Генетический способ определения понятия

Генетика и ее методология

Предмет генетики

Генетика (греч. γενητως — порождающий, происходящий от кого-то) — наука о наследственности и изменчивости. Это определение отлично соответствует афоризму А.П. Чехова «Краткость — сестра таланта». В словах наследственность и изменчивость скрыта вся сущность генетики, к изучению которой мы приступаем.

Наследственность подразумевает возможность передачи из поколения в поколение различных признаков и свойств, общих особенностей развития. Это происходит благодаря способности ДНК к самоудвоению (репликации) и дальнейшему равномерному распределению генетического материала.

Изменчивость подразумевает способность организмов приобретать новые признаки, которые отличают их от родительских особей. Вследствие этого формируется материал для главного направленного фактора эволюции — естественного отбора, который отбирает наиболее приспособленных особей.

Мы с вами — истинное чудо генетики 🙂 Очевидно, что в чем-то мы схожи с собственными родителями, в чем-то отличаемся от них. Гены, которые собраны в нас, уже миллионы лет передаются из поколения в поколение, в каждом поколении совершая чудо вновь и вновь.

Ген и генетический код

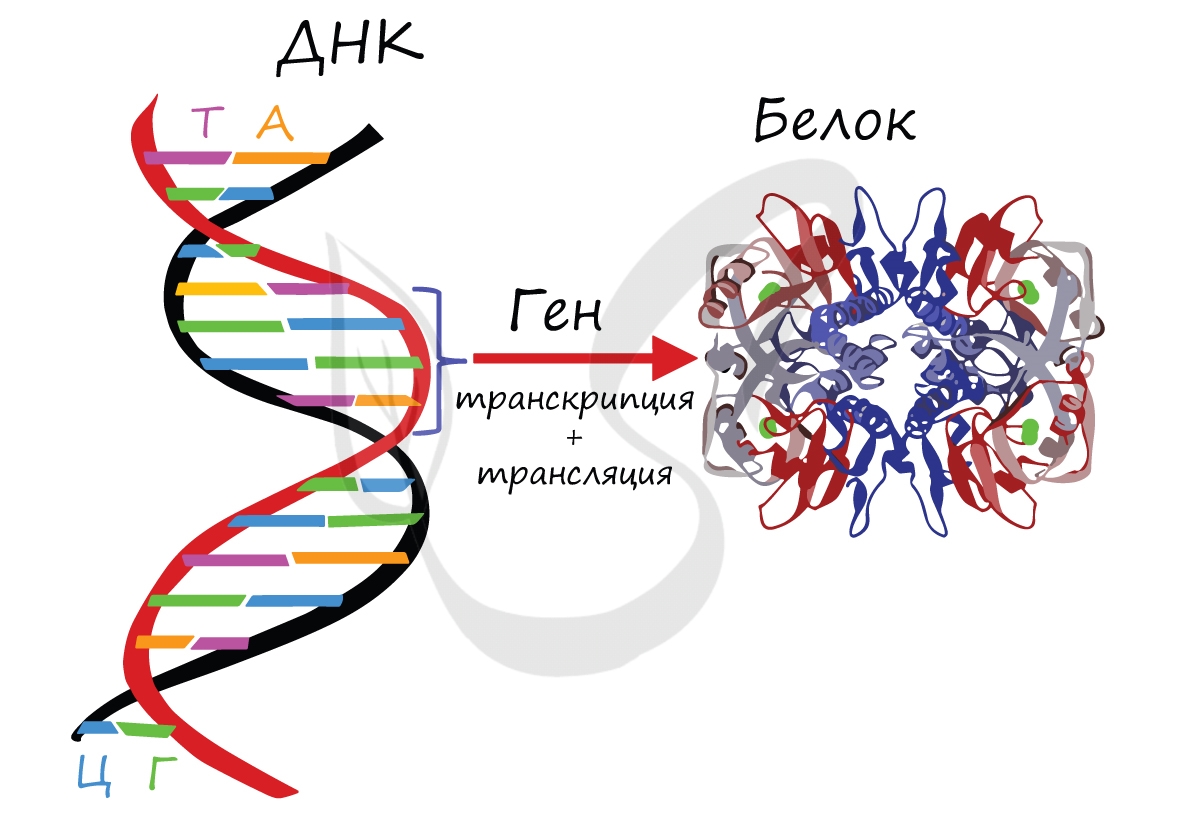
Ген — участок молекулы ДНК, кодирующий последовательность аминокислот для синтеза одного белка. Генетическая информация в ДНК реализуется с помощью процессов транскрипции и трансляции, изученных нами ранее.

В одной молекуле ДНК зашифрованы сотни тысяч различных белков. Все наши соматические клетки имеют одну и ту же молекулу ДНК. Задумайтесь: почему же в таком случае клетки кожи отличаются от клеток печени, миоцитов, клеток эпителия рта — ведь ДНК везде одинакова!

Это происходит потому, что в разных клетках одни гены «выключены», а другие «активны»: транскрипция идет только с активных генов. Именно из-за этого наши клетки отличаются по строению, функции и форме.

Способ кодирования последовательности аминокислот в белке с помощью генов — универсальный способ для всех живых организмов, доказывающий единство их происхождения. Выделяют следующие свойства генетического кода:

Триплетность

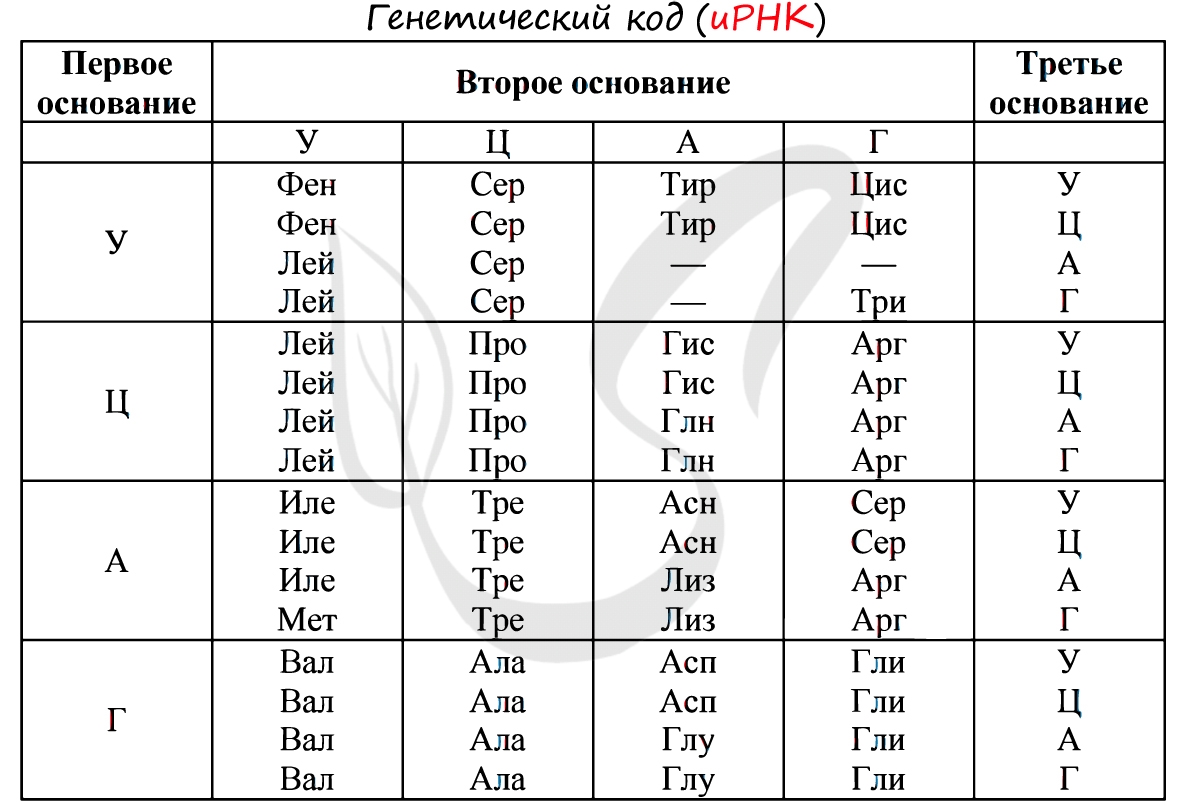
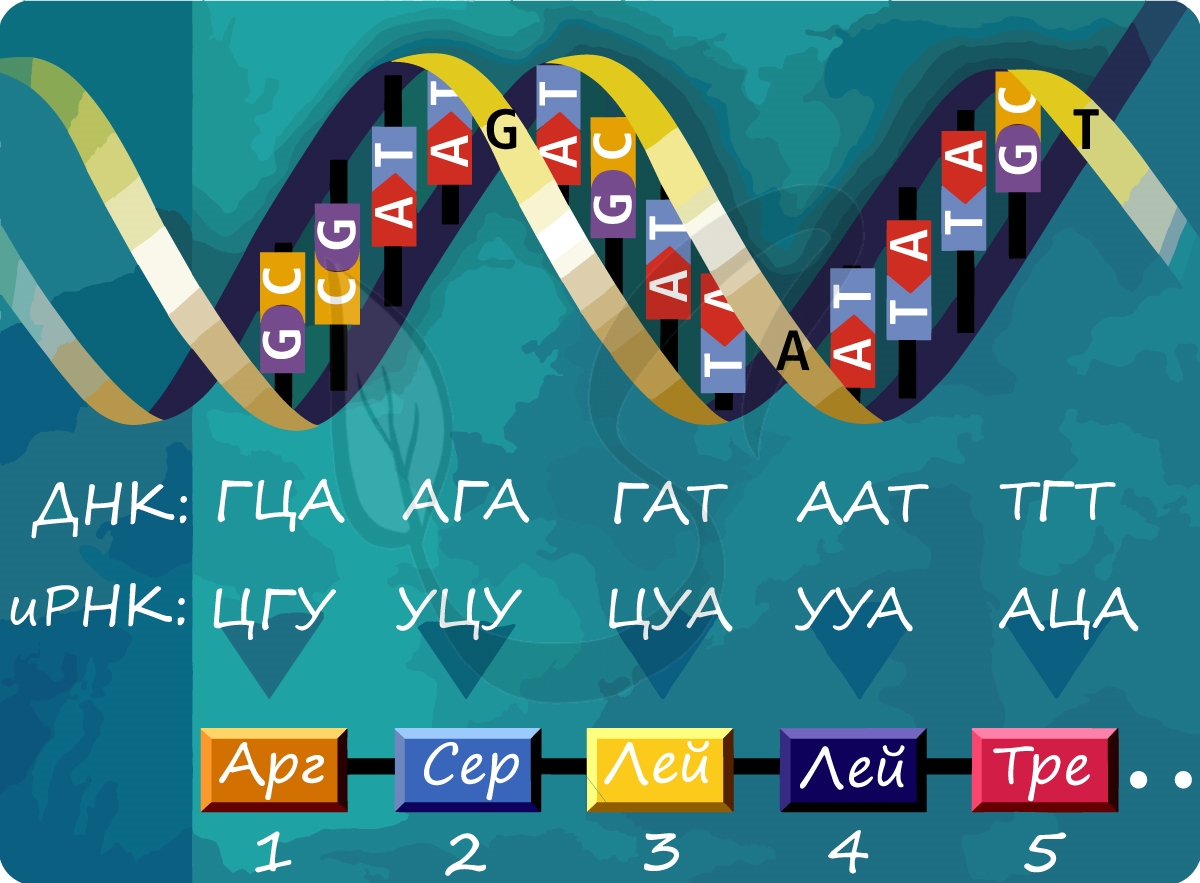
Каждой аминокислоте соответствует 3 нуклеотида (триплет ДНК, кодон иРНК). Существует 64 кодона, из которых 3 являются нонсенс кодонами (стоп-кодонами)

Информация считывается непрерывно — внутри гена нет знаков препинания: так как ген кодирует один белок, то было бы нецелесообразно разделять его на части. Стоп-кодоны — «знаки препинания» — есть между генами, которые кодируют разные белки.

Один и тот же нуклеотид не может принадлежать 2,3 и более триплетам ДНК/кодонам иРНК. Он входит в состав только одного триплета.

Один кодон соответствует строго одной аминокислоте и никакой другой более соответствовать не может.

Одна аминокислота может кодироваться несколькими кодонами (при этом одну а/к кодируют 3 нуклеотида.)

Соответствие линейной последовательности кодонов иРНК последовательности аминокислот в молекуле белка.

Кодоны считываются строго в одном направлении от первого к последующим. Считывание происходит в процессе трансляции.

Генетический код един для всех живых организмов, что свидетельствует о единстве происхождения всего живого.

Аллельные гены

Аллельные гены (греч. allélon — взаимно) — гены, занимающие одинаковое положение в локусах гомологичных хромосом и отвечающие за развитие одного и того же признака. Такими признаками могут являться: цвет глаз (карий и голубой), владение рукой (праворукость и леворукость), тип волос (вьющиеся и прямые волосы).

Локусом (лат. locus — место) — в генетике обозначают положение определенного гена в хромосоме.

Обратите внимание, что гены всегда парные, по этой причине генотип должен быть записан двумя генами — AA, Aa, aa. Писать только один ген было бы ошибкой.

Признаки бывают доминантными (от лат. dominus — господствующий), которые проявляются у гибридов первого поколения, и рецессивными (лат. recessus — отступающий) — не проявляющимися. У человека доминантный признак — карий цвет глаз (ген — А), рецессивный признак — голубой цвет глаз (ген — а). Именно поэтому у человека с генотипом Aa будет карий цвет глаз: А — доминантный аллель подавляет a — рецессивный аллель.

Генотип организма (совокупность генов — AA, Aa, aa) может быть описан терминами:

• Гомозиготный (в случае, когда оба гена либо доминантны, либо рецессивны) — AA, aa
• Гетерозиготный (в случае, когда один ген доминантный, а другой — рецессивный) — Аа

Понять, какой признак является подавляемым — рецессивным, а какой подавляющим — доминантным, можно в результате основного метода генетики — гибридологического, то есть путем скрещивания особей и изучения их потомства.

Гаметы

Гамета (греч. gamos — женщина в браке) — половая клетка, образующаяся в результате гаметогенеза (путем мейоза) и обеспечивающая половое размножение организмов. Гамета (сперматозоид/яйцеклетка) имеет гаплоидный набор хромосом — n, при слиянии двух гамет набор восстанавливается до диплоидного — 2n.

Часто в генетических задачах требуется написать гаметы для особей с различным генотипом. Для правильного решения задачи необходимо знать и понимать следующие правила:

• В гаметах представлены все гены, составляющие гаплоидный набор хромосом — n
• В каждую гамету попадает только одна хромосома из гомологичной пары
• Число возможных вариантов гамет можно рассчитать по формуле 2 i = n, где i — число генов в гетерозиготном состоянии в генотипе

К примеру для особи AABbCCDDEeFfGg количество гамет будет рассчитываться исходя из количества генов в гетерозиготном состоянии, которых в генотипе 4: Bb, Ee, Ff, Gg. Формула будет записана 2 4 = 16 гамет.

Одну гомологичную хромосому ребенок всегда получает от отца, другую — от матери

Организмы, у которых проявляется рецессивный признак — гомозиготны (аа). У гетерозигот (при полном доминировании) всегда проявляется доминантный ген (гетерозигота — Aa).

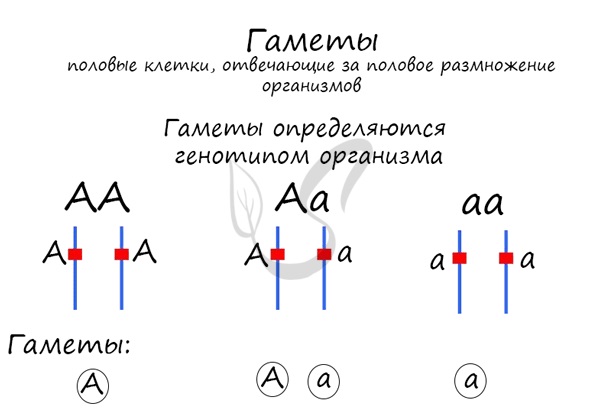
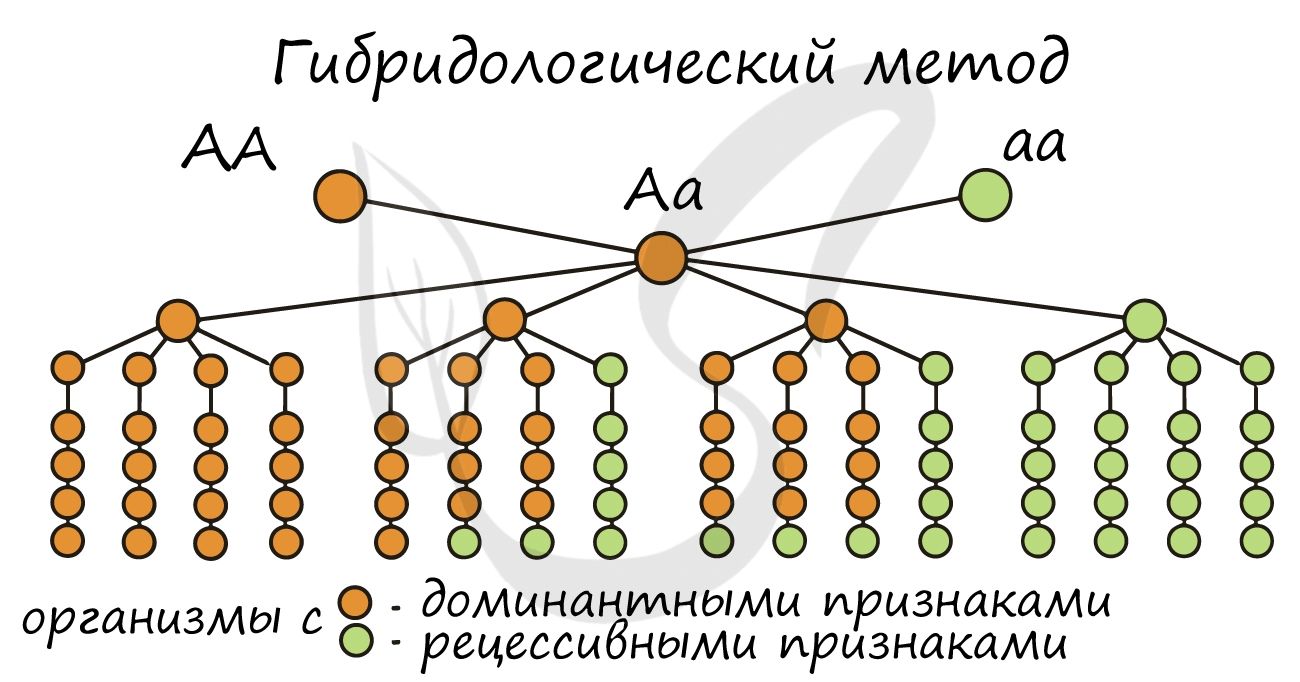
Осознайте изученные правила и посмотрите на картинку ниже. Здесь мы образуем гаметы для различных особей: AA, Aa, aa. При решении генетических задач гаметы принято обводить в кружок, не следует повторяться при написании гамет — это ошибка.

К примеру, у особи «AA» мы напишем только одну гамету «А» и не будем повторяться, а у особи «Aa» напишем два типа гамет «A» и «a», так как они различаются между собой.

Гибридологический метод

Мы приступаем к изучению методологии генетики, то есть тех методов, которые использует генетика. Один из первых методов генетики, предложенный самим Грегором Менделем — гибридологический.

Этот метод основан на скрещивании организмов между собой и дальнейшем анализе полученного потомства от данного скрещивания. С помощью гибридологического метода возможно изучение наследственных свойств организмов, определение рецессивных и доминантных генов.

Цитогенетический метод

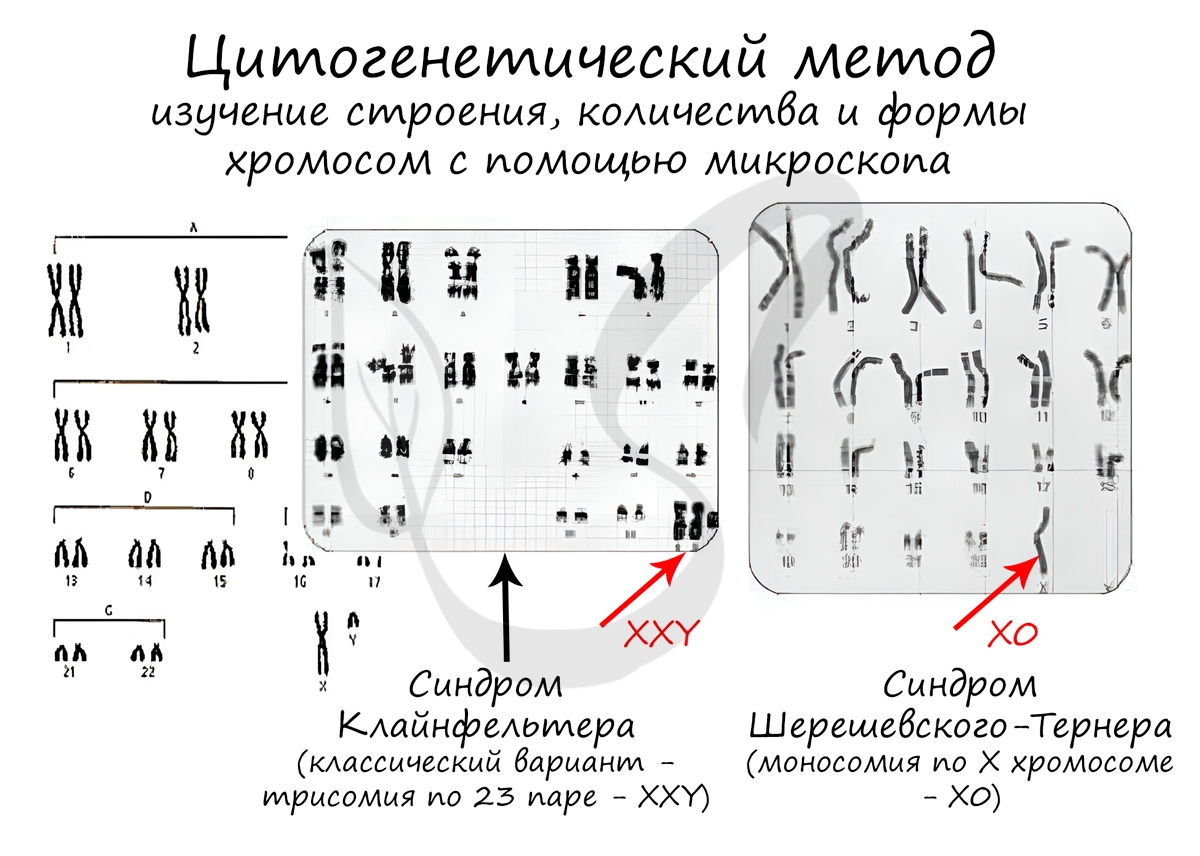
С помощью данного метода становится возможным изучение наследственного материала клетки. Врач-генетик может построить карту хромосом пациента (кариотип) и на основании этого сделать вывод о наличии или отсутствии наследственных заболеваний.

Если быть более точным, кариотипом называют совокупность признаков хромосом: строения, формы, размера и числа. При наследственных заболеваниях может быть нарушена структура хромосом (часто летальный исход), иногда нарушено их количество (синдром Дауна, Шерешевского-Тернера, Клайнфельтера).

Генеалогический метод (греч. γενεαλογία — родословная)

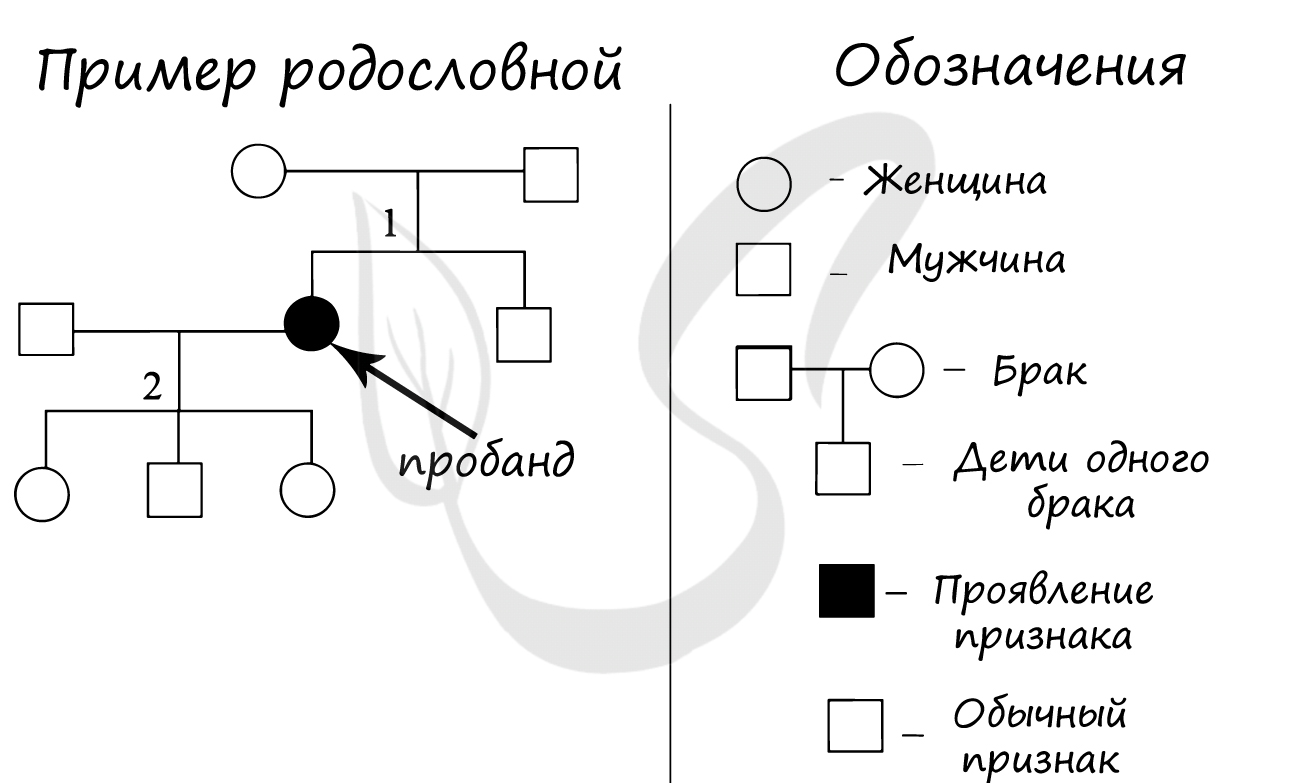
Генеалогический метод является универсальным методом медицинской генетики и основан на составлении родословных. Человек, с которого начинают составление родословной — пробанд. В результате изучения родословной врач-генетик может предположить вероятность возникновения тех или иных заболеваний.

По мере изучения законов Менделя, хромосомной теории, я непременно буду обращать ваше внимание на родословные. Вы научитесь видеть детали, по которым можно будет сказать об изучаемом признаке: «рецессивный он или доминантный?», «сцеплен с полом или не сцеплен?»

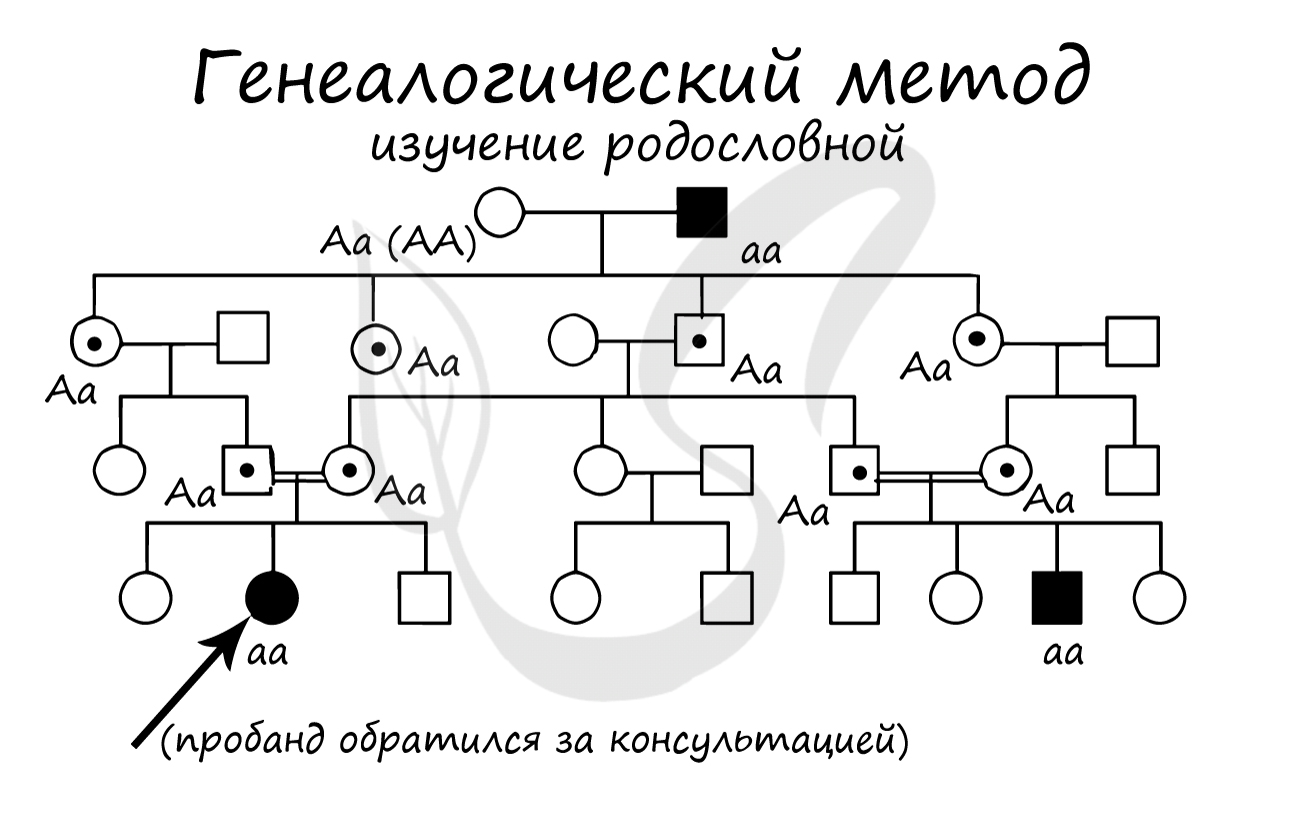
На предложенной родословной в поколениях семьи хорошо прослеживается наследование не сцепленного с полом (аутосомного) рецессивного признака (например, альбинизма). Это можно определить по ряду признаков, которые я в следующих статьях научу вас видеть. Аутосомно-рецессивный тип наследования можно заподозрить, если:

• Заболевание проявляется только у гомозигот
• Родители клинически здоровы
• Если больны оба родителя, то все их дети будут больны
• В браке больного со здоровым рождаются здоровые дети (если здоровый не гетерозиготен)
• Оба пола поражаются одинаково

Сейчас это может показаться сложным, но не волнуйтесь — решая генетические задачи вы сами «дойдете» до этих правил, и через некоторое время они будут казаться вам очевидными.

Близнецовый метод

Применение близнецового метода в генетике — вопрос удачи. Ведь для этого нужны организмы, чьи генотипы похожи «один в один»: такими являются однояйцевые близнецы, их появление подчинено случайности.

Близнецовый метод изучает влияние наследственных факторов и внешней среды на формирование фенотипа — совокупности внешних и внутренних признаков организма. К фенотипу относят физические черты: размеры частей тела, цвет кожи, форму и особенности строения внутренних органов и т.д.

Часто изучению подвергают склонность к различным заболеваниям. Интересный факт: если психическое расстройство — шизофрения — развивается у первого из однояйцевых близнецов, то у второго она возникает с вероятностью 90%. Таким образом, удается сделать вывод о значительной доле наследственного фактора в развитии данного заболевания.

© Беллевич Юрий Сергеевич 2018-2021

Данная статья написана Беллевичем Юрием Сергеевичем и является его интеллектуальной собственностью. Копирование, распространение (в том числе путем копирования на другие сайты и ресурсы в Интернете) или любое иное использование информации и объектов без предварительного согласия правообладателя преследуется по закону. Для получения материалов статьи и разрешения их использования, обратитесь, пожалуйста, к Беллевичу Юрию.

Источник

Определение математических понятий. Объем и содержание понятий. Отношения между понятиями. Способы определения понятий. Корректные и некорректные определения (Глава7. из учебного пособия «Математика» Г.М.Аматовой) , страница 2

С точки зрения языка вербальные определения являются пове­ствовательными предложениями, но не являются высказываниями в смысле математической логики. Относительно этих предложений не имеет смысла говорить истинны они или ложны. С логической точки зрения вербальные определения ближе к повелительным, чем повествовательным предложениям.

Рассмотрим некоторые способы вербальных определений.

1. Определение понятий через род и видовое отличие. Этот способ определения является наиболее распространенным, ему принадлежит ведущая роль в классической логике Аристотеля, поэтому его часто называют классическими. Логическая структура определений через род и видовое отличие проста, четко выражена и поэтому впол­не доступна учащимся уже в начальных классах школы.

Приведем примеры таких определений: «Имя существительное- это часть речи, которая обозначает пред­мет и отвечает на вопрос кто? или что?»; «Квадрат — это прямоугольник, у которого все стороны равны».

Уже из приведенных примеров видна их общая структура. В опре­делении указываются: некоторое множество (род), которому принадлежит определяемое понятие; свойство, которое выделяет определяемый объект из объектов этого же рода (видовое отличие).

Так в определении «Простым числом называется натуральное чи­сло, которое имеет точно два делителя» родовым понятием является понятие «натуральное число», а видовым отличием — свойство «иметь точно два делителя».

Если определяемое понятие обозначить через а , то его объем А выражается следующим образом: А = < х ½ хÎ В, Р(х)>. Здесь В — объем родового по отношению к а понятия, Р(х) -видовое отличие.

2. Генетическое определение понятий.

Генетические или конструктивные определения являются част­ным случаем определений через род и видовое отличие. В таких определениях видовое отличие указывает на происхождение опреде­ляемого объекта (отношения) или на способ его образования.

Рассмотрим следующее определение: «Циклоидой называется кривая линия, которую описывает любая точка окружности, катящейся по прямой без скольжения». Родовым здесь является понятие «кривая линия», а видовое от­личие указывает на способ образования определяемой кривой.

3. Рекурсивные определения.

В последнее время в математике, ее приложениях, а также в других науках все чаще встречаются, так называемые, рекурсивные определения. В таких определениях указываются некоторые основ­ные элементы из объема понятия и даются правила, позволяющие по­лучать новые элементы из уже имеющихся. Примером рекурсивного определения является определение 2.6 логической формулы. Рекур­сивные определения находят особенно широкое применение в языках программирования на ЭВМ.

Определения объектов и отношений путем указания их свойств называются дискрипциями. Примером дискрипции является опреде­ление 3.28 из §10. «Бинарное отношение р на множестве Xназывается отношением эквивалентности, если оно обладает свойствами: рефлексивности («хÎХ)(хрх); симметричности («х, у Î Х)(хру Þ урх) ; транзитивности («x, у, z Î Х)(хру Ù ypz Þ xpz)«

Здесь родовым является понятие » бинарное отношение», а видо­вое отличие представлено перечислением свойств определяемого от­ношения.

5. Аксиоматические определения.

Если какое-то понятие вводится с помощью списка аксиом, опи­сывающих свойства этого понятия, то такое определение называется аксиоматическим. Примером аксиоматического определения являет­ся следующее: «Умножением натуральных чисел называется алгебраическая опе­рация, определенная на множестве N натуральных чисел и удовле­творяющая аксиомам: 1) («а Î N)( a * 1 = а) ; 2) («a, bÎN) (a*b’ = a*b+a)»

7.4. Корректные и некорректные определения.

Для того, чтобы определения могли служить построению какой-либо научной теории, они должны удовлетворять определенным требовани­ям. Одним из самых важных таких требований является требование соразмерности определения. Это означает, что объем определяемого понятия должен совпадать с объемом определяющего понятия. Боль­шинство ошибок в определениях приводит к нарушению соразмерно­сти его частей.

Рассмотрим следующие предложения: «Биссектрисой угла называется луч, который делит угол попо­лам»; «Островом называется небольшая, по сравнению с материком, часть суши, окруженная со всех сторон морем». В первом случае объем определяющего понятия шире объема определяемого понятия (видовое отличие неполно, не сказано, что луч выходит из вершины угла), во втором — объем определяющего понятия уже объема определяемого понятия (видовое отличие суже­но, острова бывают не только в море, но и в озерах, реках).

Таким образом, ни одно из приведенных предложений не явля­ется определением, так как в обоих случаях нарушено требование соразмерности.

Другим важным требованием, предъявляемым к определениям, является отсутствие порочного круга. Нарушение этого требования проявляется в том, что определяемое понятие содержится в опреде­ляющем или в цепочке последовательных определений используют­ся термины, ранее определенные через определяемое. Поэтому, если указанное требование не выполняется, то процедура определения по­нятий «зацикливается» и не сводится к исходным понятиям.

В качестве примеров рассмотрим предложения:

1) «Будем говорить, что число а равно числу b , если число (а — b) равно нулю».

2) «Шаром называется часть пространства, ограниченная сферой», «Сферой называется граница шара».

В первом примере определяемое «равенство чисел» содержится в определяющем, а во втором — одно понятие «шар» определяется че­рез другое «сфера», и наоборот, понятие «сфера» определяется через понятие «шар».

Следующим требованием, выполнение которого необходимо для определений, является отсутствие омонимии. Каждый термин в качестве определяемого должен встречаться не более одного раза. При нарушении этого условия нарушается однозначность определения, один и тот же термин будет обозначать различные объекты или отно­шения. Нарушение этого требования особенно опасно в начале изуче­ния курса, так как создает неразбериху и вызывает дополнительные трудности при его усвоении.

В математической литературе до сих пор сохраняются некоторые омонимии. Например, слово «цифра» понимается как символ для записи числа и как соответствующее однозначное число.

При определении понятий желательно выполнение еще одного условия. Формулировка определения не должна содержать лишних свойств, которые можно вывести из других свойств, указанных в том же определении.

Рассмотрим в качестве примера определение: «Натуральное чи­сло называется простым, если оно имеет только два делителя и де­лится только на себя и единицу».

Совершенно очевидно, что условие «иметь только два делителя» вытекает из условия «делиться только на себя и на единицу», и на­оборот, а поэтому одно из этих условий является лишним.

Если определение удовлетворяет перечисленным выше условиям, то его называют корректным.

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 267
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 603
• БГУ 155
• БГУИР 391
• БелГУТ 4908
• БГЭУ 963
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 120
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1966
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 299
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 408
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 498
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 131
• ИжГТУ 145
• КемГППК 171
• КемГУ 508
• КГМТУ 270
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2910
• КрасГАУ 345
• КрасГМУ 629
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 138
• КубГУ 109
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 369
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 331
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 637
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 455
• НИУ МЭИ 640
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 213
• НУК им. Макарова 543
• НВ 1001
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1993
• НГУЭУ 499
• НИИ 201
• ОмГТУ 302
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 120
• РАНХиГС 190
• РОАТ МИИТ 608
• РТА 245
• РГГМУ 117
• РГПУ им. Герцена 123
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 123
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 131
• СПбГАСУ 315
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 146
• СПбГПУ 1599
• СПбГТИ (ТУ) 293
• СПбГТУРП 236
• СПбГУ 578
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 194
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 379
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1654
• СибГТУ 946
• СГУПС 1473
• СибГУТИ 2083
• СибУПК 377
• СФУ 2424
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 325
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 309

Полный список ВУЗов

Чтобы распечатать файл, скачайте его (в формате Word).

Источник