Генеральная совокупность способы исследования генеральной совокупности

Генеральная совокупность и выборочное исследование. Статистическая достоверность

Исследование обычно начинается с некоторого предположения, требую­щего проверки с привлечением фактов. Это предположение — гипотеза — формулируется в отношении связи явлений или свойств в некоторой сово­купности объектов.

Для проверки подобных предположений на фактах необходимо измерить соответствующие свойства у их носителей. Но невозможно измерить тревож­ность у всех женщин и мужчин, как невозможно измерить агрессивность у всех подростков. Поэтому при проведении исследования ограничиваются лишь относительно небольшой группой представителей соответствующих совокупностей людей.

Генеральная совокупность — это все множество объектов, в отношении ко­торого формулируется исследовательская гипотеза.

Например, все мужчины; или все женщины; или все жители какого-либо города. Генеральные совокупности, в отно­шении которых исследователь собирается сделать выводы по результатам ис­следования, могут быть по численности и более скромными, например, все первоклассники данной школы.

Таким образом, генеральная совокупность — это хотя и не бесконечное по численности, но, как правило, недоступное для сплошного исследования мно­жество потенциальных испытуемых.

Выборка или выборочная совокупность — это ограниченная по численности группа объектов (в психоло­гии — испытуемых, респондентов), специально отбираемая из генеральной совокупности для изучения ее свойств. Соответственно, изучение на выбор­ке свойств генеральной совокупности называется выборочным исследованием. Практически все психологические исследования являются выборочными, а их выводы распространяются на генеральные совокупности.

Таким образом, после того, как сформулирована гипотеза и определены соответствующие генеральные совокупности, перед исследователем возни­кает проблема организации выборки. Выборка должна быть такой, чтобы была обоснована генерализация выводов выборочного исследования — обобщение, распространение их на генеральную совокупность. Основные критерии обо­снованности выводов исследования — это репрезентативность выборки и ста­тистическая достоверность (эмпирических) результатов.

Репрезентативность выборки — иными словами, ее представительность — это способность выборки представлять изучаемые явления достаточно пол­но — с точки зрения их изменчивости в генеральной совокупности.

Конечно, полное представление об изучаемом явлении, во всем его диапа­зоне и нюансах изменчивости, может дать только генеральная совокупность. Поэтому репрезентативность всегда ограничена в той мере, в какой ограни­чена выборка. И именно репрезентативность выборки является основным кри­терием при определении границ генерализации выводов исследования. Тем не менее, существуют приемы, позволяющие получить достаточную для ис­следователя репрезентативность выборки (Эти приемы изучаются в курсе «Экспериментальная психология»).

Первый и основной прием — это простой случайный (рандомизированный) отбор. Он предполагает обеспечение таких условий, чтобы каждый член генеральной совокупности имел равные с другими шансы попасть в выборку. Слу­чайный отбор обеспечивает возможность попадания в выборку самых разных представителей генеральной совокупности. При этом принимаются специ­альные меры, исключающие появление какой-либо закономерности при отборе. И это позволяет надеяться на то, что в конечном итоге в выборке изу­чаемое свойство будет представлено если и не во всем, то в максимально воз­можном его многообразии.

Второй способ обеспечения репрезентативности — это стратифицирован­ный случайный отбор, или отбор по свойствам генеральной совокупности. Он предполагает предварительное определение тех качеств, которые могут вли­ять на изменчивость изучаемого свойства (это может быть пол, уровень дохо­да или образования и т. д.). Затем определяется процентное соотношение чис­ленности различающихся по этих качествам групп (страт) в генеральной совокупности и обеспечивается идентичное процентное соотношение соот­ветствующих групп в выборке. Далее в каждую подгруппу выборки испытуе­мые подбираются по принципу простого случайного отбора.

Статистическая достоверность, или статистическая значимость, результа­тов исследования определяется при помощи методов статистического выво­да.

Застрахованы ли мы от принятия ошибок при принятии решений, при тех или иных выводах из результатов исследования? Конечно, нет. Ведь наши решения опираются на результаты исследования выборочной совокупности, а также на уровень наших психологических знаний. Полностью мы не застрахованы от ошибок. В статистике такие ошибки считаются допустимыми, если они имеют место не чаще чем в одном случае из 1000 (вероятность ошибки α=0,001 или сопряженная с этим величина доверительная вероятность правильного вывода р=0,999); в одном случае из 100 (вероятность ошибки α=0,01 или сопряженная с этим величина доверительная вероятность правильного вывода р=0,99) или в пяти случаях из 100 (вероятность ошибки α=0,05 или сопряженная с этим величина доверительная вероятность правильного вывода р=0,95). Именно на двух последних уровнях и принято принимать решения в психологии.

Иногда, говоря о статистической достоверности, используют понятие «уровень значимости» (обозначается как α). Численные значения р и α дополняют друг друга до 1,000 — полный набор событий: либо мы сделали правильный вывод, либо мы ошиблись. Эти уровни не рассчитываются, они заданы. Уровень значимости можно понимать как некую «красную» линию», пересечение которой позволит говорить о данном событии как о неслучайном. В каждом грамотном научном отчете или публикации сделанные выводы должны сопровождаться указанием значений р или α, при которых сделаны выводы.

Методы статистического вывода подробно рассматриваются в курсе «Математической статистики». Сейчас лишь отметим, что они предъявляют определенные требования к численности, или объему выборки.

К сожалению, строгих рекомендаций по предварительному определению требуемого объема выборки не существует. Более того, ответ на вопрос о не­обходимой и достаточной ее численности исследователь обычно получает слишком поздно — только после анализа данных уже обследованной выбор­ки. Тем не менее, можно сформулировать наиболее общие рекомендации:

1. Наибольший объем выборки необходим при разработке диагностичес­кой методики — от 200 до 1000-2500 человек.

2. Если необходимо сравнивать 2 выборки, их общая численность должна быть не менее 50 человек; численность сравниваемых выборок должна быть приблизительно одинаковой.

3. Если изучается взаимосвязь между какими-либо свойствами, то объем выборки должен быть не меньше 30-35 человек.

4. Чем больше изменчивость изучаемого свойства, тем больше должен быть объем выборки. Поэтому изменчивость можно уменьшить, увеличивая однородность выборки, например, по полу, возрасту и т. д. При этом, естественно, уменьшаются возможности генерализации выводов.

Зависимые и независимые выборки. Обычна ситуация исследования, когда интересующее исследователя свойство изучается на двух или более выборках с целью их дальнейшего сравнения. Эти выборки могут находиться в различ­ных соотношениях — в зависимости от процедуры их организации. Независи­мые выборки характеризуются тем, что вероятность отбора любого испытуе­мого одной выборки не зависит от отбора любого из испытуемых другой выборки. Напротив, зависимые выборки характеризуются тем, что каждому испытуемому одной выборки поставлен в соответствие по определенному критерию испытуемый из другой выборки.

В общем случае зависимые выборки предполагают попарный подбор ис­пытуемых в сравниваемые выборки, а независимые выборки — независимый отбор испытуемых.

Следует отметить, что случаи «частично зависимых» (или «частично неза­висимых») выборок недопустимы: это непредсказуемым образом нарушает их репрезентативность.

В заключение отметим, что можно выделить две парадигмы психологи­ческого исследования.

Так называемая R-методология предполагает изучение изменчивости некоторого свойства (психологического) под влиянием неко­торого воздействия, фактора либо другого свойства. Выборкой является мно­жество испытуемых.

Другой подход, Q-методология, предполагает исследо­вание изменчивости субъекта (единичного) под влиянием различных стимулов (условий, ситуаций и т. д.). Ей соответствует ситуация, когда выборкой явля­ется множество стимулов.

Источник

Генеральная и выборочная совокупности, выборки

Вы будете перенаправлены на Автор24

Основные определения

Понятие выборки используется, когда надо изучить какие-либо свойства совокупности объектов. Свойства объектов можно разделить на качественные и количественные.

Пусть нам необходимо изучить совокупность партии сметаны. Тогда качественным признаком может служить срок её годности, а количественным процент содержания жиров в данной сметане.

Совокупность или выборка может быть разделена на генеральную и выборочную.

Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.

Выборочная совокупность — часть отобранных объектов из генеральной совокупности.

С понятием совокупности также связано понятие объема данной совокупности.

Объем совокупности — число объектов этой совокупности.

Понятие объема совокупности относится и к выборочной, и к генеральной совокупности.

Пусть из партии 100 пачек масла для исследования выбрано 10 пачек. Тогда объем генеральной совокупности $N=100$, а объем выборки $n=10$.

Исходя из первых двух определений, очевидно, что всегда выполняется неравенство $N>n$

Готовые работы на аналогичную тему

Помимо этих двух совокупностей выделяют также репрезентативную или представительную выборку.

Репрезентативная (представительная) выборка — выборка, в которой все объекты выбраны случайно и генеральной совокупности, то есть каждый объект генеральной совокупности имеет одинаковую вероятность попасть в выборку.

Выборка также может быть повторной и бесповторной.

Повторная выборка — выборка, при которой выбранный объект возвращается обратно в генеральную совокупность перед выбором следующего объекта для исследования.

Бесповторная выборка — выборка, при которой объект не возвращается обратно в генеральную совокупность перед выбором очередного объекта для исследования.

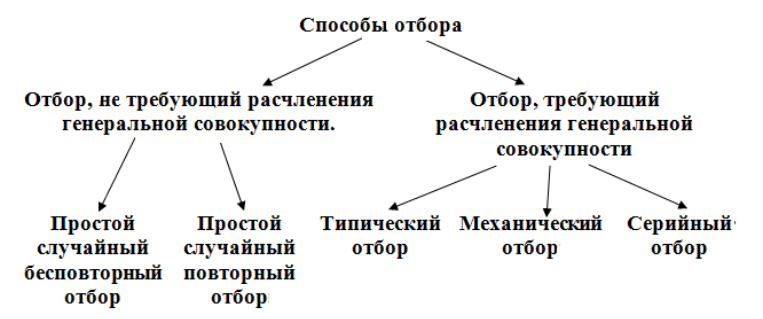
Способы отбора

Рассмотрим теперь различные способы отбора (схема 1).

Рисунок 1. Способы отбора.

Разберемся теперь с каждым понятием по отдельности.

Простой случайный бесповторный отбор — отбор, при котором объекты из генеральной совокупности выбираются по одному и не возвращаются обратно в генеральную совокупность.

Простой случайный повторный отбор — отбор, при котором объекты из генеральной совокупности выбираются по одному и возвращаются обратно в генеральную совокупность.

Типический отбор — отбор, при котором выборка производится не из всей генеральной совокупности, а из каждой его части по отдельности.

К примеру, если сметана произведена на трех разных заводах, то выборка делается по каждому заводу отдельно.

Механический отбор — отбор, при котором генеральная совокупность делится на такое количество групп сколько объектов для исследования необходимо выбрать.

Пусть из партии 100 пачек масла нужно для исследования отобрать $10\%$. Тогда выбирается по одной пачке из каждых 10 пачек масла.

. Отметим, что при таком отборе выборка не всегда получается репрезентативной.

Серийный отбор — отбор, при котором выборка происходит из генеральной совокупности не по одному, а сериями.

. На практике часто применяется комбинированный отбор, при котором используются сразу несколько видов отборов, перечисленных выше.

Формулы, связанные с понятием выборки

Введем несколько формул:

1. Генеральная средняя при повторной выборке:

Отметим, что $\sum=N$

1. Генеральная средняя при бесповторной выборке:

1. Выборочная средняя при повторной выборке:

Отметим, что $\sum=n$

1. Выборочная средняя при бесповторной выборке:

1. Ошибка репрезентативности:

Пример задачи на нахождение ошибки репрезентативности

Пусть в магазине 20 видов глазированных сырков. Средняя цена 1 вида сырка составляет 10,4 рублей. Сырков с начинкой из этих видов составляет $25\%$ и средняя цена каждого вида с начинкой равняется 11 рублей. Найти ошибку репрезентативности данной выборки.

10,4 — это генеральная средняя величина, то есть $\overline=10,4$.

Так как сырки с начинкой составляют $25\%$, то сырков с начинкой$20\cdot 0,25=5$ видов.

Источник

Генеральная совокупность и выборка

Генеральная совокупность [1] (в англ. — population) — совокупность всех объектов (единиц), относительно которых учёный намерен делать выводы при изучении конкретной проблемы.

Генеральная совокупность состоит из всех объектов, которые подлежат изучению. Состав генеральной совокупности зависит от целей исследования. Иногда генеральная совокупность — это все население определённого региона (например, когда изучается отношение потенциальных избирателей к кандидату), чаще всего задаётся несколько критериев, определяющих объект исследования. Например, мужчины 30-50 лет, использующие бритву определённой марки не реже раза в неделю, и имеющие доход не ниже $100 на одного члена семьи.

Выборка или выборочная совокупность — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании.

Характеристики выборки:

· Качественная характеристика выборки – кого именно мы выбираем и какие способы построения выборки мы для этого используем.

· Количественная характеристика выборки – сколько случаев выбираем, другими словами объём выборки.

Необходимость выборки

· Объект исследования очень обширный. Например, потребители продукции глобальной компании – огромное количество территориально разбросанных рынков.

· Существует необходимость в сборе первичной информации.

Объём выборки

Объём выборки — число случаев, включённых в выборочную совокупность. Из статистических соображений рекомендуется, чтобы число случаев составляло не менее 30 – 35.

Зависимые и независимые выборки

При сравнении двух (и более) выборок важным параметром является их зависимость. Если можно установить гомоморфную пару (то есть, когда одному случаю из выборки X соответствует один и только один случай из выборки Y и наоборот) для каждого случая в двух выборках (и это основание взаимосвязи является важным для измеряемого на выборках признака), такие выборки называются зависимыми. Примеры зависимых выборок:

· два измерения какого-либо признака до и после экспериментального воздействия,

В случае, если такая взаимосвязь между выборками отсутствует, то эти выборки считаются независимыми, например:

· мужчины и женщины,

· психологи и математики.

Соответственно, зависимые выборки всегда имеют одинаковый объём, а объём независимых может отличаться.

Сравнение выборок производится с помощью различных статистических критериев:

Репрезентативность

Выборка может рассматриваться в качестве репрезентативной или нерепрезентативной.

Пример нерепрезентативной выборки

В США одним из наиболее известных исторических примеров нерепрезентативной выборки считается случай, происшедший во время президентских выборов в 1936 году [1] . Журнал «Литрери Дайджест», успешно прогнозировавший события нескольких предшествующих выборов, ошибся в своих предсказаниях, разослав десять миллионов пробных бюллетеней своим подписчикам, а также людям, выбранным по телефонным книгам всей страны и людям из регистрационных списков автомобилей. В 25 % вернувшихся бюллетеней (почти 2,5 миллиона) голоса были распределены следующим образом:

· 57 % отдавали предпочтение кандидату-республиканцу Альфу Лэндону

· 40 % выбрали действующего в то время президента-демократа Франклина Рузвельта

На действительных же выборах, как известно, победил Рузвельт, набрав более 60 % голосов. Ошибка «Литрери Дайджест» заключалась в следующем: желая увеличить репрезентативность выборки, — так как им было известно, что большинство их подписчиков считают себя республиканцами, — они расширили выборку за счёт людей, выбранных из телефонных книг и регистрационных списков. Однако они не учли современных им реалий и в действительности набрали ещё больше республиканцев: во время Великой депрессии обладать телефонами и автомобилями могли себе позволить в основном представители среднего и высшего класса (то есть большинство республиканцев, а не демократов).

Виды плана построения групп из выборок

Выделяют несколько основных видов плана построения групп [2] :

1. Исследование с экспериментальной и контрольной группами, которые ставятся в разные условия.

2. Исследование с экспериментальной и контрольной группами с привлечением стратегии попарного отбора

3. Исследование с использованием только одной группы — экспериментальной.

4. Исследование с использованием смешанного (факторного) плана — все группы ставятся в разные условия.

Типы выборки

Выборки делятся на два типа:

Вероятностные выборки

1. Простая вероятностная выборка:

o Простая повторная выборка. Использование такой выборки основывается на предположении, что каждый респондент с равной долей вероятности может попасть в выборку. На основе списка генеральной совокупности составляются карточки с номерами респондентов. Они помещаются в колоду, перемешиваются и из них наугад вынимается карточка, записывается номер, потом возвращается обратно. Далее процедура повторяется столько раз, какой объём выборки нам необходим. Минус: повторение единиц отбора.

Процедура построения простой случайной выборки включает в себя следующие шаги:

1. необходимо получить полный список членов генеральной совокупности и пронумеровать этот список. Такой список, напомним, называется основой выборки;

2. определить предполагаемый объем выборки, то есть ожидаемое число опрошенных;

3. извлечь из таблицы случайных чисел столько чисел, сколько нам требуется выборочных единиц. Если в выборке должно оказаться 100 человек, из таблицы берут 100 случайных чисел. Эти случайные числа могут генерироваться компьютерной программой.

4. выбрать из списка-основы те наблюдения, номера которых соответствуют выписанным случайным числам

· Простая случайная выборка имеет очевидные преимущества. Этот метод крайне прост для понимания. Результаты исследования можно распространять на изучаемую совокупность. Большинство подходов к получению статистических выводов предусматривают сбор информации с помощью простой случайной выборки. Однако метод простой случайной выборки имеет как минимум четыре существенных ограничения:

1. зачастую сложно создать основу выборочногo наблюдения, которая позволила бы провести простую случайную выборку.

2. результатом применения простой случайной выборки может стать большая совокупность, либо совокупность, распределенная по большой географической территории, что значительно увеличивает время и стоимость сбора данных.

3. результаты применения простой случайной выборки часто характеризуются низкой точностью и большей стандартной ошибкой, чем результаты применения других вероятностных методов.

4. в результате применения SRS может сформироваться нерепрезентативная выборка. Хотя выборки, полученные простым случайным отбором, в среднем адекватно представляют генеральную совокупность, некоторые из них крайне некорректно представляют изучаемую совокупность. Вероятность этого особенно велика при небольшом объеме выборки.

· Простая бесповторная выборка. Процедура построения выборки такая же, только карточки с номерами респондентов не возвращаются обратно в колоду.

1. Систематическая вероятностная выборка. Является упрощенным вариантом простой вероятностной выборки. На основе списка генеральной совокупности через определённый интервал (К) отбираются респонденты. Величина К определяется случайно. Наиболее достоверный результат достигается при однородной генеральной совокупности, иначе возможны совпадение величины шага и каких-то внутренних циклических закономерностей выборки (смешение выборки). Минусы: такие же как и в простой вероятностной выборке.

2. Серийная (гнездовая) выборка. Единицы отбора представляют собой статистические серии (семья, школа, бригада и т. п.). Отобранные элементы подвергаются сплошному обследованию. Отбор статистических единиц может быть организован по типу случайной или систематической выборки. Минус: Возможность большей однородности, чем в генеральной совокупности.

3. Районированная выборка. В случае неоднородной генеральной совокупности, прежде, чем использовать вероятностную выборку с любой техникой отбора, рекомендуется разделить генеральную совокупность на однородные части, такая выборка называется районированной. Группами районирования могут выступать как естественные образования (например, районы города), так и любой признак, заложенный в основу исследования. Признак, на основе которого осуществляется разделение, называется признаком расслоения и районирования.

4. «Удобная» выборка. Процедура «удобной» выборки состоит в установлении контактов с «удобными» единицами выборки — с группой студентов, спортивной командой, с друзьями и соседями. Если необходимо получить информацию о реакции людей на новую концепцию, такая выборка вполне обоснована. «Удобную» выборку часто используют для предварительного тестирования анкет.

Невероятностные выборки

Отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности, типичности, равного представительства и т.д.

1. Квотная выборка – выборка строится как модель, которая воспроизводит структуру генеральной совокупности в виде квот (пропорций) изучаемых признаков. Число элементов выборки с различным сочетанием изучаемых признаков определяется с таким расчётом, чтобы оно соответствовало их доле (пропорции) в генеральной совокупности. Так, например, если генеральная совокупность у нас представлена 5000 человек, из них 2000 женщин и 3000 мужчин, тогда в квотной выборке у нас будут 20 женщин и 30 мужчин, либо 200 женщин и 300 мужчин. Квотированные выборки чаще всего основываются на демографических критериях: пол, возраст, регион, доход, образование и прочих. Минусы: обычно такие выборки нерепрезентативны, т.к. нельзя учесть сразу несколько социальных параметров. Плюсы: легкодоступный материал.

2. Метод снежного кома. Выборка строится следующим образом. У каждого респондента, начиная с первого, просятся контакты его друзей, коллег, знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход, респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения и т.д.)

3. Стихийная выборка – выборка так называемого «первого встречного». Часто используется в теле- и радиоопросах. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром – активностью респондентов. Минусы: невозможно установить какую генеральную совокупность представляют опрошенные, и как следствие – невозможность определить репрезентативность.

4. Маршрутный опрос – часто используется, если единицей изучения является семья. На карте населённого пункта, в котором будет производиться опрос, нумеруются все улицы. С помощью таблицы (генератора) случайных чисел отбираются большие числа. Каждое большое число рассматривается как состоящее из 3-х компонентов: номер улицы (2-3 первых числа), номер дома, номер квартиры. Например, число 14832: 14 – это номер улицы на карте, 8 – номер дома, 32 – номер квартиры.

5. Районированная выборка с отбором типичных объектов. Если после районирования из каждой группы отбирается типичный объект, т.е. объект, который по большинству изучаемых в исследовании характеристик приближается к средним показателям, такая выборка называется районированной с отбором типичных объектов.

Стратегии построения групп

Отбор групп для их участия в психологическом эксперименте осуществляется с помощью различных стратегий, которые нужны для того, чтобы обеспечить максимально возможное соблюдение внутренней и внешней валидности [3] .

· Рандомизация (случайный отбор)

· Привлечение реальных групп

Рандомизация , или случайный отбор, используется для создания простых случайных выборок. Использование такой выборки основывается на предположении, что каждый член популяции с равной вероятностью может попасть в выборку. Например, чтобы сделать случайную выборку из 100 студентов вуза, можно сложить бумажки с именами всех студентов вуза в шляпу, а затем достать из неё 100 бумажек — это будет случайным отбором (Гудвин Дж., с. 147).

Попарный отбор — стратегия построения групп выборки, при котором группы испытуемых составляются из субъектов, эквивалентных по значимым для эксперимента побочным параметрам. Данная стратегия эффективна для экспериментов с использованием экспериментальных и контрольных групп с лучшим вариантом — привлечением близнецовых пар (моно- и дизиготных), так как позволяет создать.

Стратометрический отбор — рандомизация с выделением страт (или кластеров). При данном способе формирования выборки генеральная совокупность делится на группы (страты), обладающие определёнными характеристиками (пол, возраст, политические предпочтения, образование, уровень доходов и др.), и отбираются испытуемые с соответствующими характеристиками.

Приближённое моделирование — составление ограниченных выборок и обобщение выводов об этой выборке на более широкую популяцию. Например, при участии в исследовании студентов 2-го курса университета, данные этого исследования распространяются на «людей в возрасте от 17 до 21 года». Допустимость подобных обобщений крайне ограничена.

Приближенное моделирование – формирование модели, которая для четко оговоренного класса систем (процессов) описывает его поведение (или нужные явления) с приемлемой точностью.

Источник