Гдз алгебра 7 класс способ сложения

Способ сложения

Рассмотрим ещё один способ решения систем линейных уравнений — способ сложения. При решении систем отим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Пример 1. Решим систему уравнений

В уравнениях этой системы коэффициенты при у являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной Зх = 33. Заменим одно из уравнений системы (1), например первое, уравнением Зх = 33. Получим систему

Система (2) равносильна системе (1).

Решим систему (2). Из уравнения 3х = 33 находим, что х= 11.

Подставив это значение х в уравнение

получим уравнение с переменной у:

Решим это уравнение:

Пара (11; -9) — решение системы (2), а значит, и данной системы (1).

Воспользовавшись тем, что в уравнениях системы (1) коэффициенты при у являются противоположными числами, мы свели её решение к решению равносильной системы (2), в которой одно из уравнений содержит только одну переменную.

Геометрически равносильность систем (1) и (2) означает, что графики уравнений 2x + 3у = -5 и х — 3у = 38 пересекаются в той же точке, что и графики уравнений 3x = 33 и х — 3у = 38, т. е. все три прямые пересекаются в одной точке (рис. 80).

Источник

Способ сложения (продолжение)

Пример 2. Решим систему уравнений

Почленное сложение уравнений системы не приведёт к исключению одной из переменных. Однако если умножить все члены первого уравнения на -2, а второе уравнение оставить без изменений, то коэффициенты при х в полученных уравнениях будут противоположными числами:

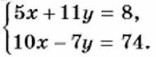
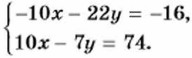
Теперь почленное сложение приводит к уравнению с одной переменной -29у = 58. Из этого уравнения находим, что у = -2. Подставив во второе уравнение вместо у число -2, найдём значение х:

10x — 7 • (-2) = 74, 10x = 60, x = 6.

Ответ. x = 6, у = -2.

Пример 3. Решим систему уравнении

Подберём множители к уравнениям системы так, чтобы после умножения на них коэффициенты при у стали противоположными числами. Умножив первое уравнение системы на -4, а второе на 5, получим

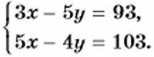
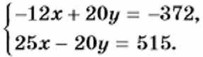
Отсюда найдём, что 13x = 143, x = 11. Подставив значение * в уравнение 5x — 4у = 103, найдём, что у = -12.

Ответ. x = 11, у = -12.

Мы рассмотрели примеры решения систем способом сложения. При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:

1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;

2) складывают почленно левые и правые части уравнений системы;

3) решают получившееся уравнение с одной переменной;

4) находят соответствующее значение второй переменной.

Заметим, что если коэффициенты при одной из переменных являются противоположными числами, то решение сразу начинают с почленного сложения уравнений.

Источник

44. Способ сложения

Рассмотрим ещё один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Пример 1. Решим систему уравнений

(1)

Решение: В уравнениях этой системы коэффициенты при у являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной Зх = 33. Заменим одно из уравнений системы (1), например первое, уравнением Зх = 33. Получим систему

(2)

Система (2) равносильна системе (1).

Решим систему (2). Из уравнения Зх = 33 находим, что х = 11. Подставив это значение х в уравнение

получим уравнение с переменной у:

Решим это уравнение:

Пара (11; -9) — решение системы (2), а значит, и данной системы (1).

Воспользовавшись тем, что в уравнениях системы (1) коэффициенты при у являются противоположными числами, мы свели её решение к решению равносильной системы (2), в которой одно из уравнений содержит только одну переменную.

Геометрически равносильность систем (1) и (2) означает, что графики уравнений 2х + 3у = -5 и х — 3у = 38 пересекаются в той же точке, что и графики уравнений Зх = 33 и х — Зу = 38, т. е. все три прямые пересекаются в одной точке (рис. 80).

Пример 2. Решим систему уравнений,

Решение: Почленное сложение уравнений системы не приведёт к исключению одной из переменных. Однако если умножить все члены первого уравнения на -2, а второе уравнение оставить без изменений, то коэффициенты при х в полученных уравнениях будут противоположными числами:

Теперь почленное сложение приводит к уравнению с одной переменной -29у = 58. Из этого уравнения находим, что у = -2. Подставив во второе уравнение вместо у число -2, найдём значение х:

10х — 7 • (-2) = 74, 10х = 60, х = 6.

Ответ: х = 6, у = -2.

Пример 3. Решим систему уравнений

Решение: Подберём множители к уравнениям системы так, чтобы после умножения на них коэффициенты при у стали противоположными числами. Умножив первое уравнение системы на -4, а второе на 5, получим

Отсюда найдём, что 13х = 143, х = 11. Подставив значение х в уравнение 5х — 4у = 103, найдём, что у = -12.

Ответ, х = 11, у = -12.

Мы рассмотрели примеры решения систем способом сложения. При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:

1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Заметим, что если коэффициенты при одной из переменных являются противоположными числами, то решение сразу начинают с почленного сложения уравнений.

Упражнения

Найдите решение системы уравнений:

Решите систему уравнений:

Решите систему уравнений:

Найдите решение системы уравнений:

Составьте уравнение вида у = kx + b, график которого проходит через точки:

График линейной функции пересекает оси координат в точках (-5; 0) и (0; 11). Задайте эту функцию формулой.

Прямая у = kx + b проходит через точки А(-1; 3) и В(2; -1). Напишите уравнение этой прямой.

График линейной функции пересекает ось х в точке с абсциссой 4, а ось у в точке с ординатой 11. Задайте эту функцию формулой.

Задайте формулой линейную функцию, график которой изображён на рисунке 81.

Рис. 81
Решите систему уравнений:

Найдите решение системы уравнений:

Решите систему уравнений:

Найдите решение системы уравнений:

Имеет ли решения система и сколько:

Разложите на множители:

Упростите выражение:

Источник

ГДЗ контрольные и самостоятельные работы по алгебре 7 класс Попов, Мордкович Экзамен

Седьмой класс – это тот самый переломный момент, когда математика для школьника делится на алгебру и геометрию. Ученику только предстоит изучить математический язык, разобрать первые числовые и алгебраические выражения, познакомиться с линейной функцией и её особенностями. Для того чтобы это процесс был быстрым и максимально комфортным, учителя рекомендуют гдз контрольные и самостоятельные работы по алгебре за 7 класс Попов как отличное учебно-практическое пособие. В соответствии с разделами учебника, решебник знакомит семиклассников с примерами выполнения заданий, предназначенных для проведения диагностических оценочных работ на уроке.

Читайте также:  Способы вертикального выравнивания css

Кому однозначно пригодиться сборник ответов?

Многие постоянно задаются вопросом, нужны ли вообще подобные решебники. Профессиональные педагоги и авторы учебной литературы практически единогласно утверждают, что да. Составленный в соответствии с требованиями Министерства Образования и Науки РФ сборник правильных решений к контрольным и самостоятельным работам по алгебре за 7 класс (авторы Попов, Мордкович) будет максимально полезным для:

• семиклассников, проявляющих стремление самостоятельно готовиться к предстоящим диагностическим работам. Несколько часов, проведенных за сравнением вариантов решений, дадут четкое понимание того, как проще выполнить определенное задание;
• восьмиклассников, которым необходимо повторить пройденный материал после летних каникул или догнать программу после дистанционного обучения. В проверочных работах, как правило, представлены самые важные задания. Их разбора с лихвой хватит для качественного повторения;
• родителей, участвующих в учебном процессе своих детей. Не помните что такое «Тождества»? Не беда! Повторите вместе с ребенком за полчаса, разобрав пару примеров решения контрольных заданий;
• учителей, проводящих внеклассные занятия. Так как в сборниках ответов авторы используют самые рациональные методы решения задач и примеров, именно их разбор на занятиях является максимально продуктивным.

В чем заключается преимущество решебника по алгебре за 7 класс к контрольным и самостоятельным работам Попов?

Разложение многочленов на множители, основные понятия и методы алгебраического сложения, системы линейных уравнений и их графическое решение – всё это больше не будет казаться таким сложным. Постоянное использование еуроки ГДЗ положительно сказывается на уровне знаний учащихся. Преимуществ много, вот основные:

• бесплатный доступ к ответам, позволяющий анализировать свой уровень знаний и тем самым экономить на услугах репетиторов;
• постоянное обновление информации на ресурсе. Если в учебнике была допущена опечатка, которую нашли лишь спустя полгода, она сразу же будет исправлена в ответе;
• полное соответствие требованиям и стандартам в плане оформления работ. Детальное объяснение заданий, требующих развернутых ответов;
• быстрый и удобный поиск по нумерации работ и вариантам, сокращающий время поисков ответа к минимуму.

Работая с изданием, семиклассник научится самостоятельно определять цели и достигать их. Подготовка по методике авторов решебника будет не сложнее, чем занятия на уроке в школе.

Источник