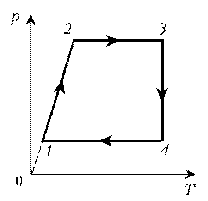
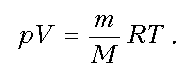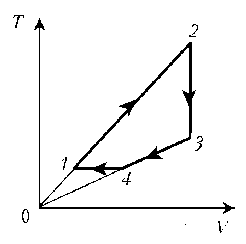Графические задачи на газовые законы
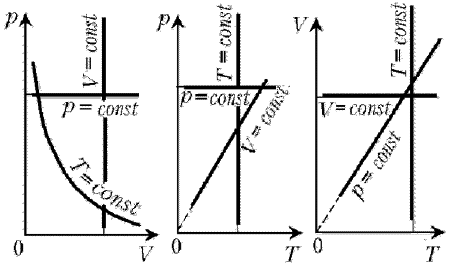
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
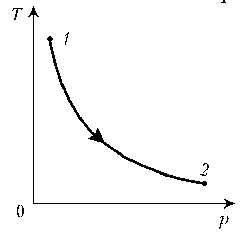
Пример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
Пример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то r 1 > r 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
Пример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
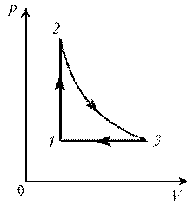
2–3: изотермический процесс; закон Бойля–Мариотта; р
3–1: изобарический процесс; закон Гей-Люссака; V
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
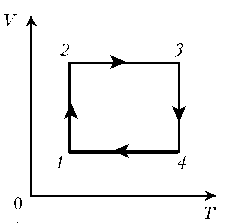
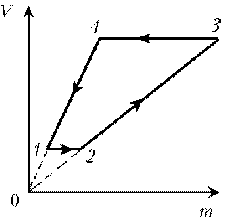
Пример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
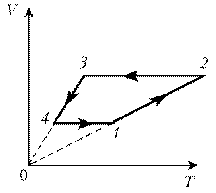
2–3: изохорический процесс; закон Шарля; р
3–4: изобарический процесс; закон Гей-Люссака; V
4–1: изохорический процесс; закон Шарля; р
T; р ; T .
Пример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
1–2: изотермический процесс; закон Бойля–Мариотта; р
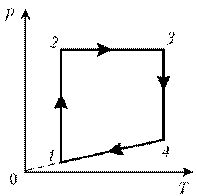
3–4: изотермический процесс; закон Бойля–Мариотта; р
4–1: изохорический процесс; закон Шарля; р
А вот блок задач с необычной постановкой условия. Впрочем, и они решаются достаточно стандартными методами, а известные формулы начинают играть новыми красками. Давайте убедимся в этом.
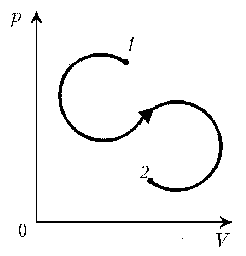
Пример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
Решение. Проведем изотермы через характерные точки 1, 2, 3 и касательную к участку 1–2. Как следует из теории, изотермы, более удаленные от координатных осей, соответствуют более высоким температурам. В этом можно убедиться, используя методы, предложенные в предыдущих задачах.
Проходим по циклу:
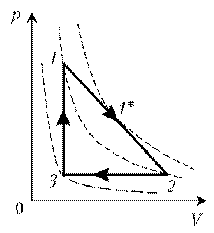
1*–2: переход на более «низкую» изотерму, следовательно, температура понижается.
2–3: переход на еще более «низкую» изотерму, это означает дальнейшее понижение температуры.
3–1: переход на более «высокую» изотерму, значит, температура повышается.
Как видим, ничего необычного в этой задаче нет, при решении использованы известные факты.
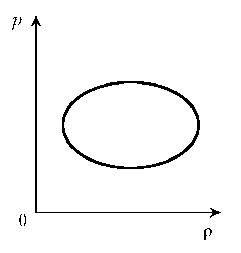
Пример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
Решение. Проведем изохоры через характерные точки 1, А, В, 2. Проведем изотерму, пересекающую все изохоры, и спроецируем эти точки пересечения на ось р. Плотность r = m/V, т.е. плотность обратно пропорциональна объему. При 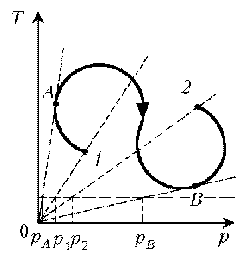
1/V. Таким образом, задача сводится к вопросу, каким изохорам соответствуют большие или меньшие объемы. Обратимся к графику:
Итак, сначала плотность уменьшается, затем увеличивается и снова уменьшается.
А это уже пример задачи, в которой «играют» формулы, позволяющие получить ответ, казалось бы, без конкретных данных.
Пример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
Решение. В наших руках есть надежное «оружие» в виде уравнения Клапейрона–Менделеева! Применим его для двух произвольных состояний, учитывая, что в этих состояниях, по условию, давления одинаковы. Выразим объем через массу и плотность: V = m/ r . Тогда:
Теперь остается разделить одно уравнение на другое:
Как известно, обратно пропорциональная зависимость изображается гиперболой. Точки ее пересечения с циклом и будут соответствовать состояниям с одинаковым давлением. Заметим: любые другие гиперболы, пересекаясь с линией графика, будут давать пары состояний с одинаковым (но уже другим) давлением.
И в заключение рассмотрим три примера, о которых говорилось выше, – задачи, в которых масса газа меняется. К сожалению, как правило, подобные задачи в школьном курсе не рассматриваются. Это и приводит к неприятностям на вступительных экзаменах: срабатывает «фактор неожиданности», и абитуриент теряется.
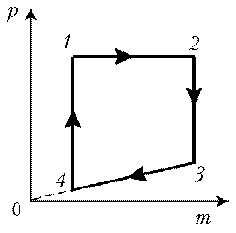
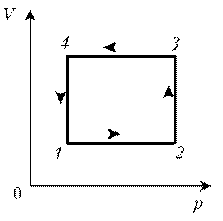
Пример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
Решение. Запишем уравнение Клапейрона–Менделеева:
Рассмотрим процессы цикла поэтапно:
1–2: T = const, V = const; m
2–3: T = const, р = const; m
3–4: T = const, V = const; m
4–1: T = const, р = const; m
V; V Ї ; m Ї
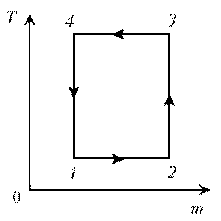
Пример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
Решение. Запишем уравнение
Клапейрона–Менделеева:
m; m ; V .
2–3: р = const; m = const; V
T; T ; V .
3–4: р = const; T = const; V
m; m Ї ; V Ї
4–1: р = const; m = const; V
Легко видеть, что ничего «необычного» в этих задачах нет, они решаются все теми же методами, которые рассматривались выше. Хочется надеяться, что после знакомства с ними у школьников и абитуриентов проблем уже не будет.
Пример 11. Дан график зависимости р(V) для процессов, проводимых с идеальным газом неизменного химического состава при постоянной температуре. Кривые 2–3 и 4–1 – гиперболы. Изобразите эти процессы в координатах m, р.
Решение. Запишем уравнение Клапейрона–Менделеева: .
1–2: T = const, р = const; V
1/V; m = const; р Ї
3–4: T = const, V = const; р
Задачи для самостоятельного решения
- 1. Изобразите цикл постоянной массы идеального газа на диаграммах V, T; р, V.
- 2. Изобразите цикл постоянной массы идеального газа на диаграммах р, T; р, V.
- 3. Как менялась плотность постоянной массы идеального газа при переходе 1–2?
- 4. Изобразите цикл постоянной массы идеального газа на диаграммах р, V и р, T.
- 5. Идеальный газ постоянной массы расширяется по закону рV 2 = const. Как при этом меняется температура газа: повышается или понижается?
- 6. Как менялась температура постоянной массы газа при переходе 1–2?
- 7. Дан цикл постоянной массы идеального газа. Указать на линии графика состояния, которым соответствуют экстремальные значения температуры.
- 8. Над постоянной массой идеального газа совершается работа по представленному циклу. Найти отношение экстремальных значений объема в цикле и изобразить цикл на диаграммах р, V; V, T.
Источник
Газовые законы. Решение задач графическим способом
Газовые законы. Решение задач графическим способом
- Формирование знаний графического способа решения задач на газовые законы и умений применять их; Развитие умений сравнивать, выявлять закономерности, обобщать, логически мыслить; Воспитывать ответственное отношение к учебному труду, активизировать познавательный интерес учащихся.
Оборудование: комплекты заданий для самостоятельной работы, карточки для проверки правильности выполнения этой работы, плакаты с графиками изопроцессов.
Организационный момент. Повторение теоретического материала по изученной теме. Самостоятельная работа и самопроверка. Способы решения физических задач. Графический способ. Объяснение нового материала. Закрепление. Самостоятельная работа и самопроверка. Постановка домашнего задания. Итоги урока.
Мы продолжаем повторять с вами молекулярную физику и на этом уроке рассмотрим графическое построение изопроцессов т. к. эти задания встречаются в материалах ЕГЭ.
ll. Повторение теоретического материала по изученной теме
— Какими тремя макроскопическими параметрами характеризуется состояние идеального газа? (Это давление, объём и температура.)
— Каким законам подчиняется данная связь? (Записать на доске: Уравнение состояния идеального газа 

— Как называют процессы, протекающие при неизменном значении одного из параметров? (Процессы, протекающие при неизменном значении одного из параметров, называют изопроцессами.)
— Давайте вспомним какие бывают изопроцессы для этого просмотрим анимацию.
Процесс изменения состояния термодинамической системы макроскопических тел при постоянной температуре называют изотермическим.
— Кто его открыл? Бойля-Мариотта
— Сформулируйте закон. (Для газа данной массы произведение давления газа на его объем постоянно, если температура газа не меняется. 
— Рассмотрим графическое изображение изотермического процесса в различных системах координат.
Графики изотермического процесса называют изотермами
В координатах (рТ) и (VТ) изотермы представляют собой прямые линии, перпендикулярные оси температур. Иначе обстоит дело в координатах (рV). Из закона Бойля – Мариотта, следует что при постоянной температуре газа его давление обратно пропорционально объёму
Разным постоянным температурам соответствуют различные изотермы. При повышении температуры давление согласно уравнению состояния увеличивается, если V = const. Поэтому изотерма, соответствующая более высокой температуре Т3, лежит выше изотермы, сответствующей более низкой температуре Т1.
Процесс изменения состояния термодинамической системы макроскопических тел при постоянном объёме называют изохорным.
— Кто его открыл? Французский физик Ж. Шарль.
— Сформулируйте закон. (Для газа данной массы отношение давления к температуре постоянно, если объём не меняется. 
— Рассмотрим графическое изображение изохорного процесса в различных системах координат.
Графики изохорного процесса называют изохорами.
В координатах (рТ) изохоры представляют собой прямые проходящие через начало координат. В системах (VТ) и (pV) изохоры представляют собой прямые линии, перпендикулярные оси объёмов.
Разным постоянным объёмам соответствуют различные изохоры. С ростом объёма газа при постоянной температуре давление его согласно закону Бойля – Мариотта падает. Поэтому изохора, соответствующая большему объёму V3, лежит ниже изохоры, соответствующей меньшему объёму V1.
Процесс изменения состояния термодинамической системы макроскопических тел при постоянном давлении называют изобарным.
— Кто его открыл? Французский учёный Ж. Гей — Люссак
— Сформулируйте закон. (Для газа данной массы отношение объёма к температуре постоянно, если давление не меняется. 
— Рассмотрим графическое изображение изобарного процесса в различных системах координат.
Графики изобарного процесса называют изобарами.
В координатах (VТ) изобары представляют собой прямые проходящие через начало координат. В системах (рV) и (pТ) изохоры представляют собой прямые линии, перпендикулярные оси давления.
Разным постоянным давлениям соответствуют различные изобары. С ростом давления объём газа при постоянной температуре согласно закону Бойля – Мариотта уменьшается. Поэтому изобара, соответствующая большему давлению р3 лежит ниже изобары, соответствующей более низкому давлению р1.
Решение графических задач.
1. Идеальный газ сначала нагревался при постоянном объёме, потом его объём увеличивался при постоянном давлении, затем при постоянной температуре давление газа уменьшалось до первоначального значения. Какой из графиков на рисунке в координатных осях р-Т соответствует этим изменениям состояния газа?
2. На рисунке изображены процессы, проходящие с определённой массой идеального газа. Изобразите эти процессы в осях (рV) и (рТ)

4. Идеальный газ (число частиц N = const) переходит из состояния 1 в состояние 2. Как меняется в этом процессе объём, занимаемый газом?
ü Сначала увеличивается, потом уменьшается
ü Сначала уменьшается, потом увеличивается.

Согласно уравнению Менделеева – Клапейрона

Источник

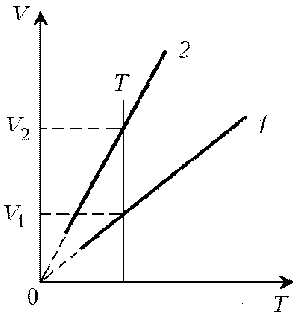 Пример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Пример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?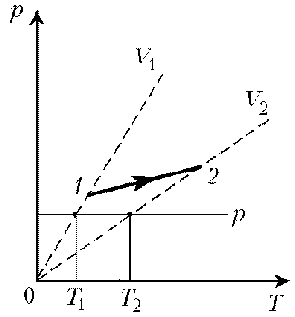 Пример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Пример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?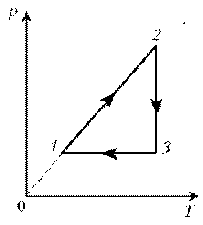 Пример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Пример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.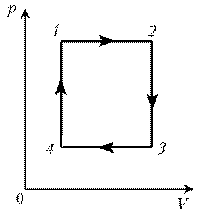 Пример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Пример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.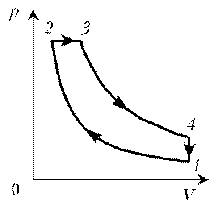 Пример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
Пример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.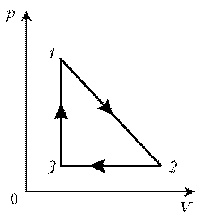 Пример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
Пример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.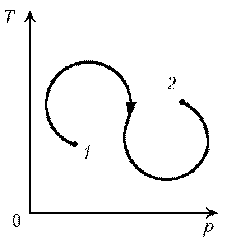 Пример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
Пример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?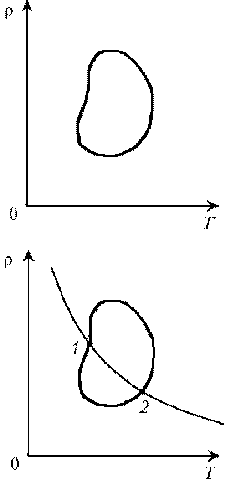 Пример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
Пример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.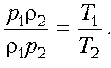
 Пример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
Пример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.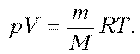
 Пример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
Пример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.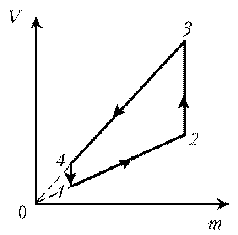
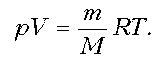
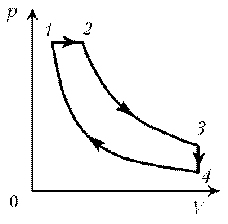 Пример 11. Дан график зависимости р(V) для процессов, проводимых с идеальным газом неизменного химического состава при постоянной температуре. Кривые 2–3 и 4–1 – гиперболы. Изобразите эти процессы в координатах m, р.
Пример 11. Дан график зависимости р(V) для процессов, проводимых с идеальным газом неизменного химического состава при постоянной температуре. Кривые 2–3 и 4–1 – гиперболы. Изобразите эти процессы в координатах m, р.