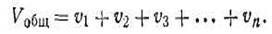- Газовые смеси закон дальтона способы задания газовых смесей
- Газовые смеси. Закон Дальтона.
- Газовые смеси. Способы их задания. Закон Дальтона.
- Газовые законы
- Понятие газовой смеси. Парциальное давление, закон Дальтона. Парциальный объем, закон Амага. Способы задания газовых смесей. Пожарная опасность смесей горючих с воздухом. Циклы газотурбинных установок. Конвективный теплообмен при движении жидкости.
- Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Газовые смеси закон дальтона способы задания газовых смесей
При описании природных явлений и процессов в технических устройствах приходится иметь дело не только с одним газом (кислородом, водородом и т. п.), но и со смесью нескольких газов. Воздух, являющийся смесью азота, кислорода, углекислого газа, аргона и других газов, – наиболее часто упоминаемый пример смеси газов.
Допустим, что смесь из $$ N$$ различных газов находится в равновесном состоянии в сосуде объёмом $$ V$$ при абсолютной температуре $$ T$$. От чего зависит общее давление $$ p$$ в сосуде, заполненном смесью газов? Исследованием этого вопроса в начале XIX века занимался английский химик Джон Дальтон.
Пронумеруем газы, входящие в состав смеси, присвоив каждому свой номер $$ i(i=\mathrm<1,2>,\dots ,N)$$. Давление $$
_$$, которое производил бы каждый из газов, составляющих смесь, если удалить остальные газы из сосуда, называют парциальным давлением этого газа. Парциальный (от латинского слова pars – часть) – частичный, отдельный. Дальтоном экспериментально установлено, что для достаточно разреженных газов давление `p_»см»` смеси газов, химически не взаимодействующих между собой, равно сумме парциальных давлений компонентов смеси:
Сейчас этот закон называют законом Дальтона.
В смеси идеальных газов каждый из газов ведёт себя независимо от других газов, занимает весь предоставленный объём (т. е. объём каждой компоненты смеси `V`), и его состояние описывается уравнением Менделеева-Клапейрона:
Здесь $$
Если теперь в равенство 6), выражающее закон Дальтона, подставить значения парциальных давлений из (7), то после несложных преобразований можно получить уравнение, описывающее состояние смеси идеальных газов:
Если ввести понятие молярная масса смеси:
то уравнение Менделеева–Клапейрона для смеси газов будет выглядеть так:
Источник
Газовые смеси. Закон Дальтона.
В практике очень часто приходится иметь дело не с чистыми газами, а с их смесями. Особенно широкое распространение газовые смеси получили в технике. Одни из них служат ценным химическим сырьем и используются при синтезе ряда веществ (нефтяные газы, воздух), другие являются хорошим газообразным топливом (природный, доменный, генераторный газы).
Основным законом газовых смесей является закон Дальтона, который имеет следующую формулировку: общее давление газовой смеси робщ равно сумме парциальных давлений всех входящих в нее газов р1+р2 + p3 + . т. е.
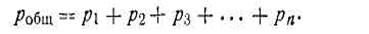 | 1.27 |
Парциальное давление — это часть общего давления в газовой смеси. Оно равно тому давлению газа, которым он обладал бы, занимая один весь объем смеси.
Как и другие законы идеальных газов, закон Дальтона не выполняется при высоких давлениях и низких температурах.
К каждому отдельному газу, входящему в данную газовую смесь, может быть применено уравнение состояния газа (I.17):
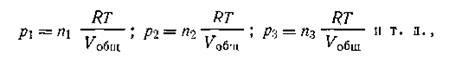 | 1.28 |
где Vобщ — общий объем газовой смеси; n1, n2, n3 . — числа молей отдельных газов в смеси.
Подставив эти выражения в (I.27) и сделав соответствующие преобразования, получим уравнение состояния применительно к смесям идеальных газов:
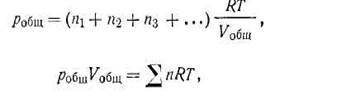 | 1.29 |
где ∑n — сумма числа молей газов в смеси.
Помимо парциального давления для газовых смесей различают парциальный объем каждого из газов: υ1, υ2, υ3 и т. д. Парциальный объем — это объем, который занимал бы отдельный газ, входящий в состав смеси идеальных газов, если бы при том же количестве он имел давление и температуру смеси.
Сумма парциальных объемов всех идеальных газов, входящих в смесь, равна общему объему смеси:
Состав газовых смесей обычно выражают в массовых и объемных долях в процентах, а также в молярных долях и молярных долях в процентах. Выражение состава газовых смесей в объемных долях в процентах широко применяется в газовом анализе.
Источник
Газовые смеси. Способы их задания. Закон Дальтона.



В практике чаще приходиться встречаться не с чистыми газами, а с их механическими смесями; одной из самых важных смесей является воздух, представляющий собой смесь азота и кислорода, с небольшой примесью аргона, углекислоты и водяного пара. Большое значение имеют такие газовые смеси, как природный газ (метан и другие углеводороды), продукты сгорания топлив (диоксид углерода, азот, водяной пар и т.п.).
Под газовой смесью понимается смесь отдельных газов, не вступающих между собой ни в какие химические реакции. Каждый газ (компонент) в смеси независимо от других газов полностью сохраняет все свои свойства и ведет себя так, как если бы он один занимал весь объём смеси.
Для проведения расчетов с газовыми смесями необходимо установить параметры, характеризующие их состояние. Пусть имеется смесь из 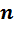
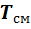
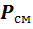
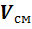
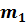
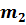
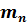
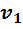
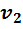
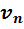
Если смесь находится в равновесии, то, несомненно, температура всех газов одинакова и равна температуре смеси 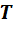
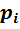
Парциальное давление – это давление, которое имел бы каждый газ, входящий в состав смеси, если бы этот газ находился один в том же количестве, в том же объёме и при той же температуре, что и в смеси.
Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси идеальных газов равно сумме парциальных давлений всех входящих в неё компонентов:
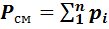
Этот закон был установлен Дальтоном в 1801 г.
Все зависимости, полученные для идеальных газов, справедливы и для их смесей, если в них подставить газовую постоянную ( 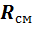
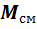
Очевидно, что масса газовой смеси равна сумме отдельных компонентов:
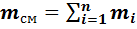
где : 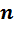
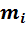
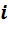
Качественный состав газовой смеси может быть задан различными способами.
Источник
Газовые законы
Понятие газовой смеси. Парциальное давление, закон Дальтона. Парциальный объем, закон Амага. Способы задания газовых смесей. Пожарная опасность смесей горючих с воздухом. Циклы газотурбинных установок. Конвективный теплообмен при движении жидкости.
| Рубрика | Производство и технологии |
| Вид | контрольная работа |
| Язык | русский |
| Дата добавления | 27.01.2016 |
| Размер файла | 515,3 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Теплотехника — наука, которая изучает методы получения, преобразования, передачи и использования теплоты, а также принципы действия и конструктивные особенности тепловых машин, аппаратов и устройств. Теплота используется во всех областях деятельности человека.
Для установления наиболее рациональных способов ее использования, анализа экономичности рабочих процессов тепловых установок и создания новых, наиболее совершенных типов тепловых агрегатов необходима разработка теоретических основ теплотехники. Различают два принципиально различных направления использования теплоты — энергетическое и технологическое.
При энергетическом использовании, теплота преобразуется в механическую работу, с помощью которой в генераторах создается электрическая энергия, удобная для передачи на расстояние. Теплоту при этом получают сжиганием топлива в котельных установках или непосредственно в двигателях внутреннего сгорания.
При технологическом — теплота используется для направленного изменения свойств различных тел (расплавления, затвердевания, изменения структуры, механических, физических, химических свойств). Количество производимых и потребляемых энергоресурсов огромно.
Теплотехника является общетехнической дисциплиной при подготовке специалистов технических специальностей и состоит из трех взаимосвязанных предметов: технической термодинамики, основ теории теплообмена, в которых исследуются законы превращения и свойства тепловой энергии и процессы распространения теплоты.
Задача курса теплотехники заключается в подготовке инженера-химика-технолога, владеющего навыками грамотного руководства проектированием и эксплуатацией современного химического производства, представляющего собой совокупность технологических и тепловых процессов и соответствующего технологического и теплоэнергетического оборудования. Эта подготовка будет способствовать успешному выполнению указанных выше задач выпускниками химико-технологических вузов. Значение такой подготовки будет расти по мере вовлечения атомной, термоядерной и возобновляемых видов энергии в ряд практически значимых и эффективных, ибо, по известному выражению, никакой вид энергии не обходится так дорого, как его недостаток.
газовый парциальный газотурбинный конвективный
Теоретический вопрос № 1
Понятие газовой смеси. Парциальное давление. Закон Дальтона. Парциальный объем. Закон Амага. Способы задания газовых смесей. Пожарная опасность смесей горючих с воздухом
Газовая смесь — это смесь нескольких идеальных газов, не вступающих между собой ни в какие химические реакции. Примерами газовой смеси могут служить: атмосферный воздух который состоит из смеси, преимущественно, азота и кислорода; природный газ; выхлопной газ двигателей внутреннего сгорания (ДВС), который содержит СО2, СО, N2, NO2, O2 и другие газы, влажный воздух(водяной пар) в сушильных установках и т. п.
Главный принцип, определяющий свойства газовой смеси, принцип независимости действия газов в смеси, то есть каждый газ в смеси действует независимо от других газов, не меняет своих свойств и подчиняется всем газовым законам. Кроме того, каждый газ занимает весь объем смеси и все газы в смеси имеют одинаковую температуру, а свойства смеси газов складываются из свойств всех ее компонентов.
Из этого следует, что газовые смеси подчиняются тем же законам и уравнениям, что и однородные идеальные газы. Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление газовой смеси идеальных газов равно сумме парциальных давлений всех входящих в нее компонентов:
где Рсм — давление газовой смеси; Р1, Р2, Рn — парциальные давления компонентов смеси.
Каждый компонент смеси, занимая весь объем смеси, находится под своим парциальным давлением. Но если этот компонент поместить под давлением Рсм при той же температуре смеси Tсм, то он займет объем меньший (Vi), чем объем смеси Vсм). Этот объем Vi называют приведенным или парциальным.
Парциальное давление вычисляется по уравнению состояния данного компонента:
Для сравнения газов входящих в смесь по объему вводится понятие парциального объема.
Парциальным (приведенным) объемом данного компонента называется условный объем, который имел бы данный компонент, если он один находился при температуре и давлении смеси. Зависимость между объемом газовой смеси и парциальными объемами отдельных газов в смеси отражает закон Амага (закон аддитивности): общий объем газовой смеси равен сумме парциальных объемов ее компонентов:
Для вычисления парциального объема запишем два уравнения состояния для какого-либо газа, входящего в смесь:
первое — когда газ, имеющий парциальное давление Р1, занимает весь объем смеси Vсм имеет температуру смеси Tсм:
второе — когда газ имеет приведенный объем Vi при давлении Рсм и температуре смеси Tсм:
Разделив первое уравнение на второе, получим уравнения состояния компонента
где Рсм и Vсм— давление и объем смеси; Рi и Vi — давление и объем i компонента.
Отсюда выразим парциальный объем компонента:
Свойства газовой смеси зависят от ее состава, который может быть задан массовыми, объёмными и мольными долями.
Массовой долей компонента смеси gi называется величина, равная отношению массы компонента к массе всей смеси:
где mi — масса данного компонента; mсм — масса всей смеси, содержащая n компонентов.
Так как масса смеси m равна сумме масс всех компонентов:
то сумма массовых долей равна:
Зная массовые доли отдельных газов, входящих в смесь, можно определить их парциальные давления
Массовые доли часто задаются в процентах. Например, для сухого воздуха: g(N2) = 77%; g(О2) = 23%.
Объемной долей компонента смеси ri называется величина, равная отношению парциального объема компонента к объему смеси:
где Vi— парциальный объем данного компонента; Vсм — объем всей смеси.
Поскольку объем смеси равен сумме парциальных объемов компонентов , то сумма объемных долей равна: .
Объемные доли задаются в процентах. Например, для воздуха: r(N2) = 79%; r(О2) = 21%.
Мольной долей компонента смеси хi называется величина, равная отношению числа молей этого компонента к общему числу молей смеси:
Так как общее число молей смеси равно сумме чисел молей каждого компонента , очевидно, что:
В соответствии с законом Авогадро объемы моля любого газа при одинаковых давлении и температуре, в частности при температуре и давлении смеси, в идеально газовом состоянии одинаковы. Поэтому приведенный объем любого компонента может быть вычислен как произведение объема моля Vм на число молей этого компонента, т.е. Vi = VмN, а объем смеси — по формуле V = VмN.
следовательно, задание газов, входящих в смесь, мольными долями равно заданию их объемными долями.
Соотношение между массовой и мольной долей можно найти из уравнения:
В итоге имеем следующие соотношения:
В полученных уравнениях МСМ — средний (кажущийся) молекулярный вес данной газовой смеси, т.е. молекулярный вес такого условного однородного газа, который по своим свойствам аналогичен данной газовой смеси.
Исходя из этого, величина МСМ определяется по составу смеси следующим образом:
Так как соотношение:
Складывая зависимости для величины gi по всем компонентам газовой смеси, имеем:
После преобразований получим:
Уравнение состояния для газовой смеси может быть принято по следующим соображениям. Из принципа независимости следует, что если каждый газ в смеси независимо от других подчиняет уравнению состояния, то и вся смесь может рассматриваться, как один однородный газ со своими особыми свойствами, который так же подчиняется уравнению состояния, т.е.
где RCM — средняя кажущаяся газовая постоянная смеси, определяемая на основе среднего молекулярного веса смеси:
Величина RCM может быть также найдена по составу смеси после подстановки зависимостей для МСМ:
Газовую постоянную смеси можно рассчитать и через массовые доли и газовые постоянные компонентов. Запишем для каждого компонента смеси уравнение Менделеева- Клапейрона:
Суммируя по всем компонентам, получим:
Сумма в левой части уравнения равна объему смеси. Поделив обе части уравнения на массу смеси m получим
Сумма в правой части уравнения представляет собой газовую постоянную смеси:
Некоторые газы и пары в определенной смеси с воздухом взрывоопасны. Пожарная опасность газовых смесей определяется концентрацией горючих газов, паров или пылей в смеси. На нижнем концентрационном пределе воспламенения (НКПВ) в смеси небольшое количество горючего и избыток воздуха. По мере повышения концентрации горючего в смеси появляется недостаток воздуха, что приводит к потере способности воспламенения.
Взрыв смеси может произойти только при определенных соотношениях горючих газов, входящих в смесь, с воздухом или кислородом, характеризуемых нижним и верхним пределами взрываемости. При выборе состава смеси учитывают границы взрываемости. Например, метано-воздушная смесь взрывоопасна при содержании 5,3—14,9% СН4, а аммиачно-воздушная смесь — при содержании 14,0—27% NН3. Таким образом, применяемая в производстве газовая смесь, содержащая 12—13% СН4 и 11—12% МН3, в воздухе взрывобезопасна. Однако такая исходная смесь находится близко к пределам взрываемости, и для предупреждения возможного нарушения состава предусматривают автоматическое регулирование соотношения газов. Для полной безопасности к исходной смеси добавляют азот.
Теоретический вопрос № 2
Циклы газотурбинных установок
Газотурбинными установками (ГТУ) называются теплоэнергетические устройства, в которых рабочим телом служат газообразные продукты сгорания топлива (или другие газы, нагретые тем или иным способом), а рабочим двигателем является газовая турбина. ГТУ относятся к числу двигателей внутреннего сгорания. Они отличаются от поршневых двигателей внутреннего сгорания тем, что полезная работа производится в них за счет кинетической энергии движущегося с большой скоростью газа.
Газотурбинные установки обладают по сравнению с поршневыми двигателями рядом технико-экономических преимуществ, а именно:
— меньшим весом и малыми габаритами установки при большой мощности;
— отсутствием кривошипного -шатунного механизма;
— равномерностью хода и возможностью непосредственного соединения с потребителями работы — электрическими генераторами, центробежными компрессорами и т.д.;
— осуществлением цикла с полным расширением и тем самым с большим термическим КПД;
— возможностью применения дешевых сортов топлива (керосин).
Эти преимущества ГТУ способствовали их распространению во многих областях техники.
Конструкция первой газовой турбины была разработана инженером-механиком русского флота П.Д. Кузьминским в 1897 г. Она предназначалась для небольшого катера. Отличительной особенностью этой турбины являлась ее работа с водяным паром, который впрыскивался в камеру сгорания для понижения температуры газов перед турбиной.
Широкое распространение ГТУ стало возможным лишь после решения двух основных проблем: создания газового компрессора с высоким КПД (турбокомпрессора) и получения новых жаропрочных сплавов металла, способных длительно работать при температурах 650 — 750 ?С и выше.
В основе работы ГТУ лежат идеальные циклы, состоящие из простейших термодинамических процессов. Термодинамическое изучение этих циклов базируется на предположениях аналогичных циклам ДВС, а именно: циклы обратимы, подвод теплоты происходит без изменения химического состава рабочего тела цикла, отвод теплоты предполагается обратимым, гидравлические и тепловые потери отсутствуют, рабочее тело представляет собой идеальный газ с постоянной теплоемкостью. В отличие от поршневых ДВС, где процессы сжатия, подвода теплоты и расширения осуществляются в одном и том же цилиндре, в газотурбинных установках эти процессы происходят в различных элементах установки, в которые последовательно попадает поток рабочего тела. ГТУ могут работать со сгоранием топлива при постоянном давлении и при постоянном объеме. Соответствующие им идеальные циклы делят на циклы:
— с подводом тепла при постоянном давлении (Р = const) — цикл Брайтона;
— с подводом тепла при постоянном объеме (v = const) — цикл Гемфри;.
— цикл с регенерацией теплоты.
Наибольшее практическое применение получил цикл с подводом тепла при постоянном давлении.
Схема и цикл ГТУ с подводом теплоты при p=const (цикл Брайтона)
Принципиальная схема газотурбинной установки, в которой сгорание топлива происходит при постоянном давлении, приведена на рис.1, а осуществляемый в ней обратимый цикл представлен в pv и Ts — диаграммах на рис.1.1. В этой установке атмосферный воздух из окружающей среды, имеющий давление р1 и температуру Т1, поступает на вход компрессора(1), вращающегося на одном валу с газовой турбиной (4). В компрессоре воздух адиабатно сжимается (1-2) до давления р2, при котором подается в камеру сгорания(3), куда поступает газообразное или жидкое топливо. Здесь при постоянном давлении происходит сгорание топлива при р=idem (2-3), вследствие чего температура получившихся газообразных продуктов сгорания повышается до значения Т3. При этой температуре и давлении р3 = р2 газ поступает в турбину (4), где при адиабатном расширении (3-4) до атмосферного давления р1 совершает работу, одна часть которой затрачивается на привод компрессора, а другая — на привод генератора, вырабатывающего электроэнергию. Из турбины (4) газ при давлении р4 =р1 выбрасывается в окружающую атмосферу(4-1), а в компрессор забирается из атмосферы новый чистый воздух.
В качестве определяющих параметров идеального цикла принимаются:
— степень повышения давления воздуха или (степень сжатия) ;
— степень предварительного расширения .
Основным термодинамическим показателем эффективности цикла является его термический КПД
Если считать рабочее тело идеальным газом с постоянной теплоемкостью, то количество подводимого тепла определяется по формуле
а количество отводимого тепла — по формуле
Тогда, термический КПД цикла
Его обычно выражают как функцию степени повышения давления у. Для адиабаты 1 — 2 имеем:
Для изобары 2 — 3
Для адиабаты 3 — 4
Подставляя полученные значения температур Т2, Т3 и Т4 в уравнение термического КПД, получим
Из формулы следует, что термический КПД ГТУ с подводом тепла при постоянном давлении зависит от степени повышения давления у и показателя адиабаты k, возрастая с увеличением этих величин.
С учетом зависимости
Следовательно, для одного и того же рабочего тела повышение степени
сжатия всегда приводит к росту КПД.
Несмотря на то, что увеличение степени повышения давления воздуха благоприятно сказывается на экономичности газотурбинной установки, повышение этой величины приводит к увеличению температуры газов перед рабочими лопатками турбины. Величины этой температуры лимитируются жаропрочностью сплавов, из которых изготовлены лопатки. В настоящее время максимально допустимая температура газов перед турбиной составляет 800 — 1000° С и дальнейшее повышение температуры может быть достигнуто только при применении новых жаропрочных материалов и внедрении конструкций турбин с охлаждаемыми лопатками.
Схема и цикл ГТУ с подводом теплоты при V=const (цикл Гемфри)
В газотурбинной установке, работающей по циклу с подводом теплоты при постоянном объеме(V=const), процесс сгорания топлива происходит при закрытых впускных и выпускных клапанах, установленных в камере сгорания. Компрессор 1, приводимый в движение турбиной 6, подает сжатый воздух в камеру сгорания 4 через управляемый клапан 7. Второй клапан 5 находится в конце камеры сгорания и предназначен для выхода продуктов сгорания на турбину. Топливо в камеру сгорания подается насосом 2, находящимся на валу турбины, через форсунку. Подача топлива должна осуществляться периодически топливным клапаном 3.
При увеличении давления клапан 5 открывается, и продукты сгорания поступают в сопловой аппарат и на лопатки турбины 6. При прохождении через лопатки турбины газ совершает работу и выбрасывается в окружающую среду.
Цикл этой установки состоит из адиабатного сжатия в компрессоре (а-с); подвода теплоты при v = const (c-z); адиабатного расширения газа в турбине (z-e); изобарной отдачи газом теплоты окружающему воздуху (е-а). Термодинамический цикл в координатах pv и Ts представлен на рисунке 2.1. Основными параметрами цикла являются:
— степень повышения давления в компрессоре ;
— степень изохорного повышения давления .
КПД цикла ГТУ с подводом теплоты при постоянном объеме определится как:
Параметры газа в характерных точках цикла определяются через начальную температуру Та из соотношений:
Подставляя эти выражения для температур в формулу термического КПД, получим:
Таким образом, значение КПД в ГТУ с подводом теплоты при постоянном объеме зависит от степени повышения давления в компрессоре и от степени повышения давления в камере сгорания, зависящего от количества подводимой теплоты (q1) в изохорном процессе.
Удельная работа за цикл определяется:
Сравнения между собой циклы с подводом теплоты при p=const и v = const видно, что при одной и той же степени повышения давления и одинаковом отводимом количестве теплоты цикл с подводом теплоты при постоянном объеме выгоднее цикла с подводом теплоты при постоянном давлении. Это объясняется большей степенью расширения в цикле v = const, а следовательно, и большими значениями термического КПД. Несмотря на это преимущество, цикл с подводом теплоты при постоянном объеме широкого применения в практике не нашел в связи с усложнением конструкции камеры сгорания и ухудшением работы турбины в пульсирующем потоке газа, хотя работы по совершенствованию этого цикла продолжаются.
Из-за сложной конструкции камеры сгорания цикл ГТУ с изохорным подводом теплоты применяется крайне редко даже несмотря на то, что имеет повышенный КПД по сравнению с циклом Брайтона.
Цикл ГТУ с регенерацией теплоты
Одной из мер повышения термического КПД ГТУ является применение регенерации тепла. Регенерация тепла заключается в использовании тепла отработавших газов для подогрева воздуха, поступающего в камеру сгорания. Регенерация теплоты возможна при условии, что Т4>Т2. Для этого в схему установки вводят дополнительное устройство — теплообменник.
Схема газотурбинной установки со сгоранием при Р = const с регенерацией тепла представлена на рисунке 3. Отличие газотурбинной установки с регенерацией тепла от установки без регенерации состоит в том, что сжатый воздух поступает из компрессора 1 не сразу в камеру сгорания 4, а предварительно проходит через воздушный регенератор — теплообменник 3, в котором он подогревается за счет тепла отработавших газов. Соответственно газы, выходящие из турбины, перед выходом их в атмосферу проходят через воздушный регенератор, где они охлаждаются, подогревая сжатый воздух. Таким образом, определенная часть тепла, ранее уносившаяся отработавшими газами в атмосферу, теперь полезно используется.
Цикл газотурбинной установки с регенерацией и с изобарным подводом тепла в P,v — и T,s — диаграммах изображен на рисунке 1.
Рис. 1 Тепловая диаграмма ГТУ с регенерацией теплоты
Рассматриваемый цикл состоит из адиабатного процесса сжатия воздуха в компрессоре 1 — 2, процесса 2 — 5, представляющего собой изобарный подогрев воздуха в регенераторе, изобарного процесса 5 — 3, соответствующего подводу тепла в камере сгорания за счет сгорания топлива, процесса адиабатного расширении газов 3 — 4 в турбине, изобарного охлаждения выхлопных газов в регенераторе 4 — 1.
Количество тепла, подводимое к рабочему телу в изобарном процессе
а отводимое в изобарном процессе
Подставляя q1 и |q2| в общее соотношение
Температуры в основных точках цикла определяются:
Термический КПД цикла ГТУ с подводом тепла при Р = const и полной регенерацией зависит от начальной температуры Т1 и температуры в конце адиабатного расширения Т4.
В реальных условиях теплота регенерации передается не полностью, так как теплообменники не идеальные. Термический КПД цикла будет зависеть от степени регенерации. Степень регенерации — это отношение количества теплота, переданного воздуху, полученного сжатым воздухом в регенераторе, к тому количеству тепла, которое он мог бы получить, будучи нагрет от Т2 до Т5 = Т4 на выходе из газовой турбины.
Термический КПД цикла ГТУ с неполной регенерацией, т.е. при r 0 С
1. По справочным данным определим молекулярные массы компонентов:
2. Вычислим газовые постоянные газов, используя значение универсальной газовой постоянной R = 8,314 кДж/кмоль•К:
R(C3H8 ) = = 0,18895 кДж/кг•К = 188,9 Дж/кг•К;
R(С2Н4 ) = = 0,2969 кДж/кг•К = 296,9 Дж/кг•К ;
R(N2) = = 0,2969 кДж/кг•К = 296,9 Дж/кг•К .
3. Определим газовую постоянную смеси:
R= 0,487•188,95 + 0,168•143,3 + 0,146•96,7 + 0,047•296,9 + 0,152•296,9 = 92,02+24,07+13,95+14,26+45,13 = 189,43 Дж/кг•К.
4. Определим объемные доли компонентов, входящих в смесь:
где Rсм — газовая постоянная смеси, Дж/(кг·К);
Ri — газовая постоянная отдельных компонентов, входящих в смесь Дж/(кг·К).
5. Рассчитаем молекулярную массу смеси:
Мсм= 0,488• 44 + 0,127•58 + 0,074•86 + 0,073•28 + 0,238•28 = 21,47 + 7,37 + 6,36 + 2,04 + 6,66 = 44 кг/кмоль.
6. Рассчитаем объем газовой смеси, выразив его из уравнения Клайперона:
Газовая смесь, находящаяся в реакторе, имеет следующий объемный состав: окись углерода =14%, азот =6%, кислород = 75%, водяные пары = 5% нагреваются от t1 до t2. Определить количество тепла, подведённого к газовой смеси. Зависимость теплоёмкости от температуры принять в соответствии со своим вариантом
1. По условию задачи следует, что зависимость теплоемкости от температуры постоянная, то есть не зависит от температуры, следовательно, теплоемкость определяем по формуле:
где С — теплоемкость газа, кДж/кмоль•К;
Мi — молекулярная масса компонента, г/кмоль.
Для двухатомных газов (азот, кислород) Cv = 20,93 кДж/кмоль•К, для водяного пара и других многоатомных газов Cv = 25 кДж/кмоль•К.
Рассчитаем теплоемкости компонентов:
Вычислим общую теплоемкость газовой смеси:
Ссм = 0,7475•0,14 + 0,7475•0,06 + 0,6541•0,75 + 1,3889•0,05 = 0,1046 + 0,0448 + 0,4906 + 0,0694 = 0,7094 кДж/кмоль•К.
2. Рассчитаем количество теплоты при постоянной теплоемкости по формуле:
Q = 4• 0,7094(1073 — 423) = 2,8376•650 = 1844,44 Дж.
Ответ: Q = 1844,44Дж.
Воздух работает по циклу с изохорным подводом тепла. Определить параметры цикла в характерных точках и полезную работу цикла, если масса воздуха, начальное давление, начальная температура, степень сжатия и количество подведённого во время сгорания тепла соответственно равны
Цикл с изохорным подводом тепла (цикл Отто) состоит из двух адиабат и двух изохор. Характеристиками цикла являются:
степень повышения давления — ;
Количество подведенной и отведенной теплоты определяются по формулам:
Работа цикла определяется:
1. Определим параметры цикла в характерных точках.
а) Определим параметры в точке 1.
Р1 = 90•10 3 Па; Т1 = 298 К; Мвозд=28,97 кг/кмоль.
Газовая постоянная воздуха равна
Рассчитаем удельный объем воздуха V1 выразив его из уравнения Клайперона:
б) Определим параметры в точке 2.
Степень сжатия равна
Из уравнения адиабаты (процесс 1-2 — адиабатное сжатие) выразим температуру
где k — показатель адиабаты (для воздуха равен 1,4).
Давление Р2 находим из выражения
в) Определим параметры в точке 3.
Так как 2 — 3 — изохора, то V3= V2 = 0,7125 м 3 /кг.
Температуру в точке 3 определяем из соотношения
Принимая Мсv = 20,98 кДж/кг•К, М(возд) = 28,97 кг/кмоль, получаем
Давление Р3 определим из соотношения
г) Определим параметры в точке 4.
отсюда выразим давление в точке 4
2. Определим полезную работу цикла.
Вычислим количество отведенной теплоты:
Полезная работа в цикле равна
Найти наибольшую степень сжатия в цикле с изохорным подводом теплоты, если известно, что начальное давление 100 кПа, показатель адиабаты 1.3, а начальная температура и температура самовоспламенения горючей смеси составляют:
Так как происходит изохорный подвод тепла, то из уравнения адиабаты выразим степень сжатия:
Вычислим степень сжатия:
Ответ: степень сжатия ?max в цикле с изохорным подводом теплоты равна 26,9. Чем больше степень сжатия, тем выше эффективность цикла.
Воздух вытекает из резервуара. Найти значение давления среды, при котором теоретическая скорость адиабатного истечения будет равна критической и величину этой скорости, если первоначальное давление и температура соответственно равны
Воздух является двухатомным газом, следовательно, критическое значение для воздуха равно 0,528.
Из отношения выразим и найдем давление среды Р2:
Определим величину в и сравним ее с критическим значением для воздуха: 0,528 = 0,528.
Так как адиабатное истечение газа происходит при в ? вкр, то теоретическая скорость истечения газа будет равна критической скорости и определяется по формуле
Теоретический вопрос №3
Конвективный теплообмен при вынужденном движении жидкости. Теплообмен при вынужденном движении жидкости по каналам.
Конвективный теплообмен — совместный процесс конвекции и теплопроводности, так как при движении жидкости или газа неизбежно происходит соприкосновение отдельных частиц, имеющих различные температуры.
Конвективный теплообмен между потоком жидкости или газа поверхностью твердого тела называют конвективной теплоотдачей, которая
часто сопровождается теплоотдачей излучением.
В зависимости от причины, вызывающей движение жидкости, различают два рода движения: свободное (естественная конвекция) и вынужденное (вынужденная конвекция).
Свободное движение возникает вследствие разности плотностей нагретых и холодных частиц жидкости, что вызывает появление подъемной силы. Частицы жидкости, соприкасающиеся с нагретой поверхностью тела, нагреваются и становятся легче находящихся над ними холодных частиц. Такое расположение частиц неустойчиво: холодные частицы стремятся опуститься и вытеснить более легкие нагретые частицы, которые должны совершить восходящее движение навстречу опускающимся холодным частицам. Возникает сложное беспорядочное движение, в котором сталкиваются восходящие и нисходящие потоки. Чем больше перёдается тепла, тем интенсивнее свободное движение жидкости. Количество передаваемого тепла пропорционально поверхности тела и разности температур теплоотдающей (или тепловоспринимающей) поверхности и жидкости. Разностью температур определяется подъемная сила движения, а поверхностью — зона распространения процесса теплообмена.
Вынужденное движение возникает под влиянием силового воздействия на жидкость извне — насосом, ветром, вентилятором, компрессором, эжектором и др. В этом случае устанавливается разность давлений жидкости на входе и выходе из канала, по которому движется жидкость. Движущая сила определяется главным образом перепадом давлений. Интенсивность теплообмена при вынужденном движении жидкости зависит от её скорости движения, рода и физических свойств жидкости, ее температуры, формы и размеров канала, в котором происходит теплообмен.
Интенсивность процесса конвективного теплообмена ограничивается процессом теплопроводности на границе жидкости с твердой поверхностью и в пограничном слое относительно неподвижных частиц жидкости, прилегающем к твердой поверхности. Интенсивность конвективного теплообмена может быть увеличена при увеличении скорости движения жидкости относительно твердой поверхности, что способствует уменьшению толщины пограничного слоя. Этот процесс включает две стадии и два вида переноса тепловой энергии:
— перенос тепловой энергии конвекцией в объеме жидкости или газа;
-перенос тепловой энергии теплопроводностью в тонком малоподвижном слое жидкости или газа, непосредственно прилегающем к твердой стенке и называемом пограничным слоем или ламинарным подслоем;
— передача тепла теплопроводностью при непосредственном соприкосновении частиц жидкости или газа с частицами твердой стенки непосредственно на границе твердой поверхности.
Исходя из приведенных положений получено основное уравнение конвективного теплообмена, называемое уравнением Ньютона-Рихмана:
где q — удельный тепловой поток при конвективном теплообмене, Вт/м 2 ;
Q — полный тепловой поток, Вт;
F — поверхность конвективного теплообмена, м 2 ;
лж — коэффициент теплопроводности жидкости (газа) в пограничном слое, Вт/м 2 •К ;
дп.сл. — толщина пограничного слоя жидкости (газа), прилегающего к поверхности теплообмена, м;
б — коэффициент теплоотдачи, характеризующий условия теплообмена между жидкостью и твердой стенкой, Вт/м 2 •К.
Коэффициент теплоотдачи б — основная характеристика процесса конвективного теплообмена и является сложной функцией большого количества независимых величин, характеризующих явление.
Одной из основных задач конвективного теплообмена является определение в конкретных условиях коэффициента теплоотдачи. Аналитическое определение коэффициента теплоотдачи, как правило, невозможно, т.к. его величина зависит от многих переменных: параметров процесса, физических констант, геометрических размеров и граничных условий. Коэффициент теплоотдачи определяют по эмпирическим формулам, которые составляются в критериальной форме по правилам теории подобия. Два процесса конвективного теплообмена считаются подобными, если подобны все параметры, характеризующие конвективный теплообмен.
Для упрощения процесса установления подобия используют безразмерные комплексы физических параметров — числа или критерии подобия. Чисел подобия много. Для конвективного теплообмена
используют следующие пять чисел подобия.
Число Рейнольдса характеризует режим течения жидкости или газа и выражает отношение сил инерции (скоростного напора) к силам вязкостного трения:
где w — средняя скорость жидкости или газа, м/с;
l — характерный размер, м;
v — коэффициент кинематической вязкости, м 2 /с.
При числах Рейнольдса, меньших 2000, режим считается ламинарным, при значениях числа, больших 10000, — режим движения турбулентный; при значениях числа от 2000 до 10000 — режим переходный.
Число Прандтля устанавливает соотношение между толщиной
динамического и теплового пограничных слоёв:
где а — коэффициент температуропроводности, м 2 /с;
n — коэффициент кинематической вязкости, м 2 /с.
Число Нуссельта характеризует интенсивность конвективного теплообмена между жидкостью (газом) и поверхностью твёрдого тела:
где б- коэффициент теплоотдачи, Вт/(м 2 ЧК);
l — характерный размер, м;
л — коэффициент теплопроводности газа или жидкости, Вт/(мЧК).
Число Грасгофа характеризует интенсивность свободного конвективного теплообмена:
где g = 9,81 м/с 2 — ускорение свободного падения;
b — коэффициент объемного расширения: для жидкостей b приведены в справочниках (приложение Л), для газов — b = 1/Т, 1/ К;
l — характерный размер, м;
Дt — разница температур частиц жидкости (газа);
n — кинематическая вязкость, м 2 /с.
Число Эйлера характеризует отношение перепада давления к скоростному напору:
где ДР — перепад давления на участке канала, Па;
r — плотность жидкости (газа), кг/м 3 ;
w — скорость жидкости (газа), м/с.
При проектировании теплообменных аппаратов необходимо определить два параметра: коэффициент теплоотдачи б и перепад давления ДР. Они входят в числа Нуссельта и Эйлера, т.е. это определяемые числа подобия. Числа Рейнольдса, Грасгофа и Прандтля являются определяющими. Уравнения подобия — зависимость между определяемым числом подобия и определяющими числами подобия. Таким образом, при моделировании основной целью является нахождение уравнений:
Общее уравнение подобия для конвективного теплообмена имеет вид
где c, n, m, d — коэффициенты, которые определяются экспериментальными исследованиями.
В критериальных уравнениях множитель учитывает направление теплового потока отношением, при этом Pr — число Прандтля для жидкости (газа) при её температуре; Prст — число Прандтля для жидкости (газа) при температуре стенки.
Физические параметры, входящие в формулы, должны быть взяты при определяющей температуре, которая указывается для каждого случая теплообмена, причем применяют следующие определяющие температуры:
t СТ — средняя температура стенки;
tж — средняя температура жидкости или газа;
t ПЛ — средняя температура пограничного слоя (пленки), определяется, как среднее арифметическое между tж и t СТ.
Средняя температура жидкости (газа) приближенно может быть определена как среднее арифметическое между начальной и конечной температурой жидкости.
Процесс теплоотдачи при течении жидкости в трубах является более сложным по сравнению с процессом теплоотдачи при омывании плоской поверхности неограниченным потоком, при котором текущая вдали от тела жидкость не испытывает влияния процессов, идущих у стенки. Поперечное сечение трубы имеет конечные размеры. В результате в трубе, начиная с некоторого расстояния от входа, жидкость по всему поперечному сечению испытывает тормозящее действие сил вязкости. Из-за конечных размеров трубы происходит изменение температуры жидкости как по сечению, так и по длине канала. Все это сказывается на теплоотдаче.
Течение жидкости в трубах может быть ламинарным, переходным и турбулентным.
При ламинарном или слоистом, спокойном, струйном движении струи жидкости повторяют очертания канала или стенки, т.е не перемешиваются. Распространение тепла в направлении, перпендикулярном направлению движения обусловлено исключительно теплопроводностью.
При турбулентном движении происходит постоянное перемешивание жидкости. Скорость частицы жидкости в каждый момент времени перемена по величине и по направлению. При турбулентном режиме теплопроводностью тепло передаётся только в вязком подслое, а внутри турбулентного ядра этот процесс осуществляется путём интенсивного перемешивания частиц жидкости.
Переход ламинарного режима в турбулентный и наоборот происходит при определённых условиях. Параметры перехода определяются числом Рейнольдса. Так, например, для гладких труб это число примерно равно 2300.
При ламинарном движении жидкости различают два режима: вязкостный и вязкостно-гравитационный.
Вязкостным называется режим движения, когда силы вязкости преобладают над подъемными силами в жидкости. Такой режим движения имеет место при вынужденном движении вязких жидкостей и исчезающе малом влиянии свободного движения. Вязкостный режим движения обычно наблюдается при ламинарном движении жидкостей с большой вязкостью в трубах малого диаметра и при малых температурных напорах.
Вязкостно-гравитационным режимом называется режим движения жидкости, когда подъемные силы достаточно велики: на вынужденное движение накладывается свободное движение, влиянием которого на перенос количества тепла нельзя пренебрегать. В этом случае распределение скорости по сечению трубы зависит не только от изменения вязкости, но и от интенсивности и направления свободного движения жидкости, обусловленного разностью плотностей менее и более нагретых частиц жидкости.
При развитом турбулентном режиме (Re>10000) используют следующее уравнение:
где еl — поправочный множитель, учитывающий влияние начального участка потока на коэффициент теплообмена в трубе.
Определяющей температурой является средняя температура жидкости или газа. Характерным размером l является: для круглой трубы — внутренний диаметр трубы d; для трубы произвольной формы — эквивалентный диаметр dэкв
F — площадь поперечного сечения канала, м 2 ;
П — полный периметр сечения, независимо от того, какая часть этого периметра участвует в теплообмене, м.
Для газов формула упрощается, т.к. в этом случае критерий Pr является практически постоянной величиной, не зависящей от температуры, Pr = 0,67…1,0 (определяется количеством атомов в молекуле): .
При теплообмене в изогнутых трубах (змеевиках) вследствие центробежного эффекта в поперечном сечении трубы возникает вторичная циркуляция, наличие которой приводит к увеличению коэффициента теплоотдачи. Поэтому коэффициент теплоотдачи следует умножить на поправочный коэффициент езм:
где d — диаметр трубы, м; D — диаметр спирали змеевика, м.
В случае ламинарного течения жидкости (Re 2 , тела называют его лучеиспускательной (излучательной) способностью. Этот параметр излучения в пределах элементарного участка длин волн dл называют спектральной плотностью потока собственного излучения Eл, Вт/м 3 , или спектральной лучеиспускательной способностью тела, или спектральной интенсивностью излучения.
Энергия теплового излучения, падающего на тело, по закону сохранения энергии может поглощаться, отражаться телом или проходить через него:
Отношение поглощенной части энергии к падающей энергии теплового излучения называют поглощательной способностью тела и обозначают буквой А. Отношение отраженной части энергии к падающей энергии теплового излучения называют отражательной способностью тела и обозначают буквой R. Отношение прошедшей сквозь тело энергии к падающей энергии теплового излучения называют пропускательной способностью тела и обозначают буквой D. Таким образом, по закону сохранения энергии записывают:
Тело, поглощающее всю падающую на его поверхность лучистую энергию, называют абсолютно черным телом (АЧТ). Для абсолютно черного тела поглощательная способность А = 1.
Тело, отражающее всю падающую на его поверхность лучистую энергию, называют абсолютно белым телом (если отражение происходит в пределах полусферы) или зеркальным (если угол падающего луча равен углу отраженного луча). В этом случае отражательная способность R = 1.
Тело, пропускающее всю падающую на его поверхность лучистую энергию, называют прозрачным или диатермичным. В этом случае пропускательная способность D = 1.
Твердое тело не пропускает падающую на его поверхность энергию теплового излучения и поэтому
Сумму собственного излучения и части падающей энергии, которая отражается поверхностью тела, называют эффективным излучением тела:
Результирующим тепловым потоком излучения называют разность между собственным излучением и частью падающей энергии, которую тело поглощает телом:
В зависимости от характеристики течения процессы теплообмена происходят при установившемся (стационарном) режиме, когда температуры во всех точках постоянные во времени и неустановившемся (нестационарном) режиме.
Законы лучистого теплообмена были получены для абсолютно черного тела в условиях стационарного режима.
Рассмотрим основные законы лучистого излучения.
Закон Стефана — Больцмана устанавливает взаимосвязь между излучательной способностью и температурой абсолютно черного тела:
где Eо — излучательная способность абсолютно-черного тела, Вт/м 2 ;
уо =5,67Ч10- 8 ,- константа излучения абсолютно черного тела, Вт/м 2 ЧК 4 ;61
Со = 5,67-коэффициент излучения абсолютно черного тела, Вт/м 2 ЧК 4 ;
Т -абсолютная температура излучающего тела, К.
Е — излучательная способность серого тела, Вт/м 2 ;
С — коэффициент излучения серого тела, Вт/(м 2 ЧК 4 ).
Если разделить энергию излучения серого тела на энергию излучения абсолютно чёрного тела, получим:
где e — степень черноты тела.
Если принять, что С=С0Чe, то энергию излучения серого тела можно записать как:
Степень черноты может варьироваться от 0 до 1. Она зависит не только от физических свойств тела, но и от состояния ее поверхности или шероховатости.
Как видно из формулы, зависимость энергии от абсолютной температуры имеет четвертичную зависимость, поэтому основная часть теплоты при пожарах передаётся лучистым теплообменом.
Закон Кирхгофа гласит, что отношение излучательной способности тела к его поглощательной способности одинаково для поверхностей всех серых тел (при одинаковой температуре) и равно излучательной способности абсолютно черного тела при той же температуре:
где E и A — излучательная и поглощательная способности тел.
Из закона Кирхгофа вытекают три следствия:
1) в природе не существует таких поверхностей, которые излучали бы больше энергии, чем абсолютно черное тело (при одинаковой температуре);
2) тела с большей поглощательной способностью обладают большей плотностью излучения, и наоборот;
3) поглощательные способности и степени черноты реальных (серых) тел численно равны (А=е).
Закон Ламберта устанавливает зависимость между количеством излучаемой энергии и направлением излучения:
ЕН — количество энергии, излучаемой в направлении нормали.
Закон Ламберта получен для абсолютно черного тела, для серых тел с шероховатой поверхностью этот закон справедлив при ц 0 .
Для полированных поверхностей закон Ламберта неприменим, для них лучеиспускание при угле будет большим, чем в направлении, нормальном к поверхности.
Закон Вина утверждает, что максимум интенсивности излучения соответствует следующему значению длины волны:
Из формулы видно, что максимум излучения с повышением температуры смещается в сторону коротких волн (иначе закон Вина называют законом смещения).
Источник