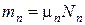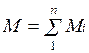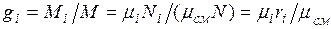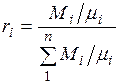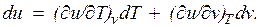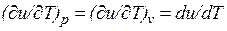Газовые смеси способы задания смесей газов

ЛЕКЦИЯ 3. Способы задания состава смеси

Способы задания состава смеси. Соотношения между ними

Смеси идеальных газов. Закон Дальтона

В ТТД чистым веществом наз. вещество, все молекулы которого одинаковы. Смесь, состоящая из нескольких чистых веществ наз. раствором. Чистыми веществами явл., например, вода, этиловый спирт, азот, аммиак и т.п. Чистые вещества, составляющие смесь, наз. компонентами.

При рассмотрении смесей газов исходят из того, что смесь идеальных газов, не вступающих в химическое взаимодействие друг с другом, так же явл. идеальным газом и подчиняется таким же законам. При этом каждый газ, входящий в состав газовой смеси, ведет себя так, как будто он один при данной температуре Т занимает весь объём смеси, т.е. равномерно распространяется по всему объёму смеси и оказывает на стенки сосуда своё давление, наз. парциальным.

В 1801г. английский учёный Дальтон экспериментально установил связь между парци- альными давлениями отдельных газов и давлением смеси. При постоянной температуре полное давление смеси нескольких газов равно сумме их парциальных давлений:

, (2.21)

где p_і— парциальное давление i-го газа; n-количество газов, составляющих газовую смесь.

Газовая смесь может быть задана массовыми, объёмными и мольными долями.

Газовая смесь, заданная массовым составом, характеризуется массовыми долями. Массовой долей компонента g_i наз. отношение массы отдельного компонента m_i, входящего в смесь, к массе всей смеси М_см, т.е.

, (2.22)

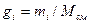
Очевидно, что масса газовой смеси равна сумме масс всех входящих в неё газов:

(2.23)

Определим сумму массовых долей отдельных газов:

, (2.24)

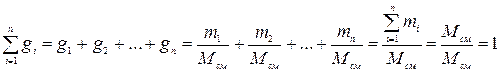
Массовые доли часто задаются в процентах (%).

Газовая смесь, заданная объёмным составом, характеризуется объемными долями (r_i). Объёмная доля каждого газа выражается отношением приведенного объёма газа V_i к полному объёму смеси V_см.

, (2.25)

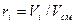
Приведенным V_i наз. объём, который занимал бы компонент газа, если бы его давление р_i и температура Т_i равнялись давлению р_см и температуре Т_см.

Парциальный объём каждого газа определяется по закону Бойля-Мариотта. При T=const.=T_см

, (2.26)

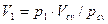
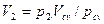
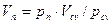
Из уравнений (2.26) имеем: ; ; … , (2.27)

Сложив отдельно левые и правые части уравнений (2.27), получим:

, (2.28)

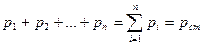
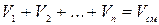
По закону Дальтона , следовательно

, (2.29) То есть сумма парциальных объёмов газа,

составляющих смесь, равна объёму смеси газов (закон Амала).

Сумма объёмных долей газов, составляющих смесь, равна единице

, (2.30)

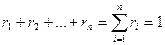
Объёмные доли часто задаются в процентах (%).

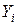
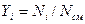
Газовая смесь, заданная мольным составом, характеризуется мольными долями. Мольной долей наз. отношение количества молей N_i рассматриваемого компонента к общему количеству молей смеси N_i. , (2.31)

Вполне очевидно, что сумма молей всех газов, составляющих смесь, равна общему числу молей газовой смеси, т.е. 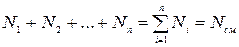, (2.32)

Сумма мольных долей смеси газов равна единице: 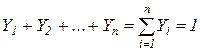, (2.33)

Если известен массовый состав смеси, то по нему можно найти её мольный состав. Массы отдельных газов m_i и полную массу смеси М_см можно выразить через число молей следующем образом: ; ; …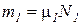

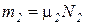
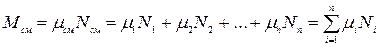
, (2.34)

2.8. Теплоёмкость. Массовая, объёмная и молярная теплоемкости.

Теплоемкости при постоянных объёме и давлении

Теплоёмкостью наз. количество теплоты, необходимое для повышения температуры тела на один градус. Теплоёмкость не является постоянной величиной и в общем случае изменяется с изменением температуры и давления. Теплоёмкость единицы количества вещества наз. удельной теплоёмкостью. Удельная теплоёмкость тела зависит от химического состава, параметров состояния рабочего тела, а также от вида процесса, в котором телу сообщается

теплота, поскольку теплота есть функция процесса. Размерность удельной теплоёмкости:

Дж/(кг(м 3 , (моль))) К).

В ТТД различают удельные массовую с, (Дж/(кг К)), объемную с’ , (Дж/(м 3 К)) и мольную с_µ (Дж/(моль К)) теплоёмкости.

Зависимости между удельными теплоёмкостями устанавливаются из следующих выражений:

; , где , (2.35)

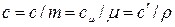
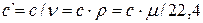
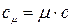
Различают истинную и среднюю теплоёмкости.

Истинной теплоёмкостьюназ. производная от количества теплоты, подведённой к телу, по температуре этого тела и определяется выражением:

, (2.36)

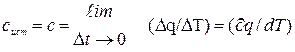
То есть истинная теплоёмкость тела – это его теплоёмкость при данной температуре.

Средней теплоёмкостью наз. теплоёмкость в интервале температур Т₂ – Т₁, она обозначается С_m. При уменьшении разности температур средняя теплоёмкость приближается к истинной.

, (2.37)

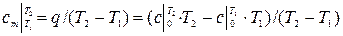
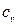
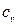
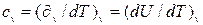
Удельной изохорной теплоемкостью наз. количество теплоты, которое необходимо подвести к рабочему телу в изохорном процессе с тем, чтобы изменить его

температуру на 1 К. , (2.38)

Удельной изобарной теплоемкостью 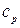наз. количество теплоты, которое необходимо подвести к рабочему телу в изобарном процессе с тем, чтобы изменить его температуру на 1 К. , (2.39)

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Смеси идеальных газов

ЛЕКЦИЯ 2

Все зависимости, полученные выше для идеальных газов, справедливы и для их смесей, если в них подставлять газо­вую постоянную, молекулярную массу и теплоемкость смеси.

Закон Дальтона.В инженерной прак­тике часто приходится иметь дело с газо­образными веществами, близкими по свойствам к идеальным газам и пред­ставляющими собой механическую смесь отдельных компонентов различных газов, химически не реагирующих между собой. Это так называемые газовые сме­си. В качестве примера можно назвать продукты сгорания топлива в двигателях внутреннего сгорания, топках печей и па­ровых котлов, влажный воздух в сушиль­ных установках и т. п.

Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси иде­альных газов равно сумме парциальных давлений всех входящих в нее компо­нентов:

Парциальное давление pi — давление, которое имел бы газ, если бы он один при той же температуре занимал весь объем смеси.

Способы задания смеси.Состав га­зовой смеси может быть задан массовы­ми, объемными или мольными долями.

Массовой долей называется отношение массы отдельного компонента Мi, к массе смеси М:

.

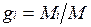
Очевидно, что и .

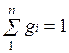
Массовые доли часто задаются в процентах. Например, для сухого воздуха ; .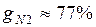

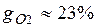
Объемная доля представляет собой отношение приведенного объема газа V, к полному объему смеси V: .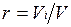

Приведенным называется объем, который занимал бы компонент газа, ес­ли бы его давление и температура равня­лись давлению и температуре смеси.

Для вычисления приведенного объема запишем два уравнения состоя­ния i-го компонента:

; (2.1)

.

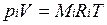
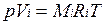
Первое уравнение относится к состоянию компонента газа в Смеси, когда он имеет парциальное давление pi и занимает пол­ный объем смеси, а второе уравнение — к приведенному состоянию, когда давле­ние и температура компонента равны, как и для смеси, р и Т. Из уравнений следует, что

. (2.2)

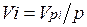
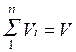
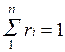
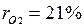
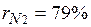
Просуммировав соотношение (2.2) для всех компонентов смеси, получим с учетом закона Дальтона ,откуда . Объемные доли также часто задаются в процентах. Для воз­духа ,.

Иногда бывает удобнее задать со­став смеси мольными долями. Моль­ной долей называется отношение количества молей Ni рассматриваемого компонента к общему количеству молей смеси N.

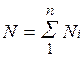
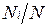
Пусть газовая смесь состоит из N1 молей первого компонента, N2 молей вто­рого компонента и т. д. Число молей смеси , а мольная доля компонента будет равна .

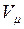
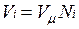
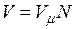
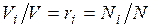
В соответствии с законом Авогадро объемы моля любого газа при одинако­вых р и Т, в частности при температуре и давлении смеси, в идеально газовом состоянии одинаковы. Поэтому приве­денный объем любого компонента может быть вычислен как произведение объема моля на число молей этого компо­нента, т. е. а объем смеси — по формуле . Тогда , и, следовательно, задание смесильных газов мольными долями равно заданию ее объемными долями.

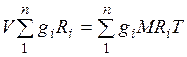
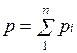
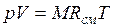
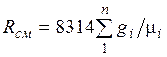
Газовая постоянная смеси газов. Просуммировавуравнения (2.1) для всех компонен­тов смеси, получим . Учитывая , можно записать

, (2.3)

. (2.4)

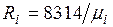
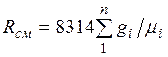
Из уравнения (2.3) следует, что смесь идеальных газов также подчиняется уравнению Клапейрона. Поскольку то из (2.4) следует, что газовая постоянная смеси [Дж/(кг-К)] имеет вид

(2.5)

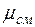
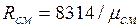
Кажущаяся молекулярная масса смеси. Выразим формально газовую постоянную смеси R, введя кажущуюся окулярную массу смеси : (2.6)

Сравнивая правые части соотношений (2.5) и (2.6), найдем

.

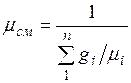
Изопределения массовых долей следует, что

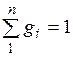
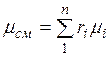
Просуммировав это соотношение для всех компонентов и учитывая, что , получим выражение для кажущейся молекулярной и массы смеси, заданной объемными долями:

. (2.7)

Соотношение между объемными и массо­выми долями. Учитывая (2.7), получаем .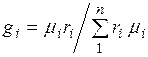

Поскольку 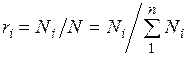, то

Разделив числитель и знаменатель этой формулы на массу смеси М, получим

.

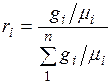
Аналитическое выражение первого закона термодинамики

Первый закон термодинамики пред­ставляет собой частный случай всеобще­го закона сохранения и превращения энергии применительно к тепловым явле­ниям. В соответствии с уравнением Эйн­штейна 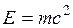надо рассматривать единый закон сохранения и превращения массы и энергии. Однако в технической термодинамике мы имеем дело со столь малыми скоростями объекта, что дефект массы равен нулю, и поэтому закон со­хранения энергии можно рассматривать независимо.

Закон сохранения и превращения энергии является фундаментальным за­коном природы, который получен на ос­нове обобщения огромного количества экспериментальных данных и применим ко всем явлениям природы. Он утвер­ждает, что энергия не исчезает и не воз­никает вновь, она лишь переходит из одной формы в другую, причем убыль энергии одного вида дает эквивалентное количество энергии другого вида.

В числе первых ученых, утверждав­ших принцип сохранения материи и энер­гии, был наш соотечественник М. В. Ло­моносов (1711 — 1765 гг.).

Пусть некоторому рабочему телу с объемом V и массой М, имеющему тем­пературу Т и давление р, сообщается из­вне бесконечно малое количество тепло­ты 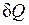. В результате подвода теплоты тело нагревается на dT и увеличивается в объеме на dV.

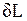
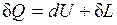
Повышение температуры тела свиде­тельствует об увеличении кинетической энергии его частиц. Увеличение объема тела приводит к изменению потенциаль­ной энергии частиц. В результате внут­ренняя энергия тела увеличивается на dU. Поскольку рабочее тело окружено средой, которая оказывает на него дав­ление, то при расширении оно произво­дит механическую работу против сил внешнего давления. Так как никаких других изменений в системе не происхо­дит, то по закону сохранения энергии

(2.8)

т. е. теплота, сообщаемая системе, идет на приращение ее внутренней энергии и на совершение внешней работы.

Полученное уравнение является ма­тематическим выражением первого зако­на термодинамики. Каждый из трех чле­нов этого соотношения может быть поло­жительным, отрицательным или равным нулю. Рассмотрим некоторые частные случаи.

1. — теплообмен системы с ок­ружающей средой отсутствует, т. е. теп­лота к системе не подводится и от нее не отводится. Процесс без теплообмена на­зывается адиабатным. Для него уравнение (2.8) принимает вид:

.

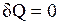
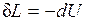
Следовательно, работа расширения, совершаемая системой в адиабатном процессе, равна уменьшению внутренней энергии данной системы. При адиабат­ном сжатии рабочего тела затрачивае­мая извне работа целиком идет на увели­чение внутренней энергии системы.

2. — при этом объем тела не изменяется, dV=0 . Такой процесс на­зывается изохорным, для него

,

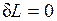
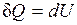
т. е. количество теплоты, подведенное к системе при постоянном объеме, равно увеличению внутренней энергии данной системы.

3. dU=0 – внутренняя энергия системы не изменяется и

,

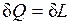
т.е. сообщаемая системе теплота пре­вращается в эквивалентную ей внешнюю работу.

Для системы, содержащей 1 кг рабо­чего тела

. (2.9)

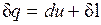
Проинтегрировав уравнения (2.8) и (2.9) для некоторого процесса, полу­чим выражение первого закона термоди­намики в интегральной форме:

; .

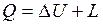
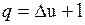
Внутренняя энергия системы включа­ет в себя:

кинетическую энергию поступатель­ного, вращательного и колебательного движения частиц;

потенциальную энергию взаимодей­ствия частиц;

энергию электронных оболочек атомов;

В большинстве теплоэнергетических процессов две последние составляющие остаются неизменными. Поэтому в даль­нейшем под внутренней энер­гией будем понимать энергию хаотиче­ского движения молекул и атомов, вклю­чающую энергию поступательного, вра­щательного и колебательного движений как молекулярного, так и внутримолекулярного, а также потенциальную энергию сил взаимодействия между молекулами.

Кинетическая энергия молекул явля­ется функцией температуры, значение потенциальной энергии зависит от сред­него расстояния между молекулами и, следовательно, от занимаемого газом объема V, т. е. является функцией V. По­этому внутренняя энергия U есть функ­ция состояния тела.

Для сложной системы она определя­ется суммой энергий отдельных частей, т. е. обладает свойством аддитивности. Величина и=U/М, называемая удельной внутренней энер­гией (Дж/кг), представляет собой внутреннюю энергию единицы массы ве­щества.

В дальнейшем для краткости будем называть величину и просто внутренней энергией. Поскольку внутренняя энергия есть функция состояния тела, то она мо­жет быть представлена в виде функции двух любых независимых параметров, определяющих это состояние:

; ; .

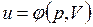
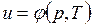
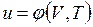
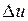
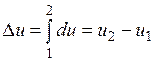
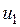
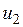
Ее изменение в термодинамическом процессе не зависит от характера процесса и определяется только началь­ным и конечным состояниями тела:

;

— значение внутренней энергии в начальном состоянии, а — в конечном. Математически это означает, что бесконечно малое измене­ние внутренней энергии du есть полный дифференциал и; если выразить внутрен­нюю энергию в виде функции удельного объема и температуры, то

Внутренняя энергия идеального газа, в котором отсутствуют силы взаимодей­ствия между молекулами, не зависит от объема газа или давления 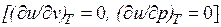, а определяется только его температурой, поэтому производная от внутренней энергии идеального газа по температуре есть полная производная:

Для задач технической термодинами­ки важно не абсолютное значение внут­ренней энергии, а ее изменение в различ­ных термодинамических процессах. По­этому начало отсчета внутренней энер­гии может быть выбрано произвольно. Например, в соответствии с международ­ным соглашением для воды за нуль при­нимается значение внутренней энергии при температуре 0,01 °С и давление 610,8 Па, а для идеальных газов — при 0 °С вне зависимости от давления.

Источник