Газовые смеси способы выражения состава смесей

Способы выражения состава газовых смесей и расчет их физико-химических характеристик (Mсм, ρсм, Δг)

Автор работы: Пользователь скрыл имя, 16 Января 2014 в 00:29, практическая работа

Описание работы

Рассмотрим физические свойства природных газов.
Единицей количества вещества является моль [n] .Это такое количество вещества, в котором содержится столько же структурных элементов, сколько атомов в 12 г углерода-12.
Причем масса 1 моля вещества в граммах m численно равна его относительной (в углер. единицах) молекулярной массе М.м. Поэтому моль условно называют грамм-молем или килограмм-киломолем.

Файлы: 1 файл

5,6 Теория Фпл.doc

Практическое занятие 5

Способы выражения состава газовых смесей и расчет их физико-химических

Рассмотрим физические свойства природных газов.
Единицей количества вещества является моль [n] .Это такое количество вещества, в котором содержится столько же структурных элементов, сколько атомов в 12 г углерода-12.

Причем масса 1 моля вещества в граммах m численно равна его относительной (в углер. единицах) молекулярной массе М.м. Поэтому моль условно называют грамм-молем или килограмм-киломолем.

Молярная масса — физическая величина, равная отношению массы к количеству вещества.

Размерность в СИ — [кг/моль]. Молярная масса, выраженная в [г/моль; кг/км] численно равна относительной молекулярн ой массе. М [г/моль; кг/кмоль]=М.м

Идеальным называется газ, в котором не учитывается взаимодействие молекул и наличие у них собственного объема.

Для идеальных газов справедливы следующие уравнения состояния, связывающие между собой P, V, T газа:

Бойля- Мариотта PV = const T = const

Гей-Люссака V/T = const P = const

Шарля P/T = const V = const

По закону Авагадро 1 киломоль любого газа при Н.У. (Р = 0,101МПа=1атм, Т =273К) занимает объем 22,4 м 3 (а 1 моль — 22,4 л), называемый нормальным молярным объемом V_м. [м 3 /кмоль]

При СТ.У. (Р=0,101МПа, Т=293К) стандартный молярный объем V_м=24,05м 3 (из закона Гей-Люссака). [Vм=объем газа м 3 /1кмоль.]

Общая зависимость между параметрами для 1 моля или 1 киломоля газа:

Было установлено, что const в этом уравнении для 1 киломоля газа равно R — универсальной газовой постоянной. R=8,3*10 3 [Дж/кмоль*град]. А для n кмолей газа, занимающих объем V, обобщенное уравнение состояния — уравнение Менделеева- Клапейрона

PV=nRT или PV=GRT — для его произвольной массы G

V — объем газа [м 3 ];

G — масса газа, [кг](G=n*M_г, n-число кмолей, M_г-молекулярная масса газа);

(R =R/Mг-удельная газовая постоянная в [Дж/кг*град ]), T-абсолютная температура ( = 273 К ).

А через молярный объем V_м (т.е. для 1 моля или кмоля газа) 1 моль — 22,4 л (= 22,4 * 10-3 м3)

Плотность газа в Н.У. или СТ.У. определяется по формуле

М_г — молекулярная масса, V_м — молярный объем в Н.У. (=22.4) или СТ.У. (=24.05)

При производственных расчетах используют относительную плотность газа по воздуху

При СТ.У. ρ_{воздуха}=1,205

Компонентный состав газовой или жидкой смеси может быть выражен в виде массовой или молярной концентрации. Сумма долей всех компонентов, составляющих смесь равна 1.

Массовая концентрация или доля i компонента в смеси определяется

где m_i — масса этого компонента,

k — число компонент

Σm_i— сумма всех имеющихся масс в смеси

По закону Авогадро для газов, молярная доля в Н.У. и СТ.У совпадает с обьемной.

Молярная (или объемная) доля i компонента Ni определяется как:

к- число компонентов

Σn_i— сумма всех имеющихся масс в смеси

На практике состав газовой смеси обычно приводят в объемных т.е. молярных концентрациях.

Если молярная концентрация компонента Ni выражена в долях, то ΣN_i, равную 1 принимают за 1 кмоль.

Если молярная концентрация компонента Ni выражена в %, то ΣN_i равную 100% принимают за 100 кмоль.

Массы компонент смеси, при известном молярном составе Σni [кмоль]

Массы компонентов в смеси с неизвестным абсолютным составом находят через N_i доли

Если молярная концентрация каждого газа N_i задана в долях ед., то ΣN_i которая равна 1, принимают за 1 кмоль. Тогда m_i компонента в [кг] приходится на 1 кмоль смеси. [кг в 1 кмоль кг * 1 кмоль ]

Если молярная концентрация каждого газа задана в %, то ΣN_i , которая равна 100%, принимают за 100 кмоль. Тогда молярная доля каждого i компонента выраженная в %, численно равна числу его кмоль. Т.е N_i в % численно равно N_i в кмоль

И m_i компонента [кг] приходится на 100 кмоль смеси

СН₄ m=300 кг М=16,04 кг/кмоль

С₃Н₈ m=500 кг М=44, 097 кг/кмоль

1. Найти число молей

2. Найти молярную долю в смеси

3.Массы компонентов при известной молярной массе

4.Массы компонентов при неизвестном молярном составе

Если N_i в долях то m на 1 киломоль смеси. Если N_i в %, m на 100 киломоль.

Молярная масса в кмоль численно равна молекулярной массе.

Связь между молярной и массовой долей i компонента

N_i в долях или %, то G_i в долях ( 7 )

Мольная доля через массовую

G_i в долях или % — N_i в долях

Здесь, если массовый состав G_i выражен в %, то его ΣG_i принимают за 100 кг. И для определения молярной доли каждого компонента N_i надо его массу G_i ( численно равную процентному содержанию этого компонента в смеси) разделить на его молекулярную массу M_i . Т.е. если G_i в %, то N_i — в долях единицы.

Массовые доли G_i Если даны только молярные N_i доли или %, то G_i

300 0,432 * 16,04 6,929

1200 0,432 * 16,04 + 0,307 * 30,07 + 0,261*44,097 27,669

С2Н6 = —- = 0,333 G = ———- = 0,334

C3H8 = —— = 0,417 G = ———— = 0,416

Если молярные (объемные) доли (Ni) компонент выражены в %, то средняя молекулярная масса газовой смеси

[ кг / кмоль ] ; Ni [ % ] , Mi [ кг /кмоль ] (8)

А если молярные доли выражены в долях единиц, то средняя молекулярная масса газ. смеси

Плотность смеси газов и относительную плотность смеси по воздуху определяют по формулам, аналогичным 2, 3, но где вместо М_г и ρ_г будут стоять М_см и ρ_см.

Δ_см =ρ_см /1,293 (при Н.У) или (1,205 — при С.У.)

Средняя молекулярная масса

Средняя плотность смеси

1. N_i — объемные доли компонент смеси газов в С.У в [ % ]

2. M_i — молекулярные массы компонент

метан СН₄ M_i = 16, 043 [кг/кмоль]

m_i — массы компонент в [кг] ф.6

G_i — массовая концентрация каждого компонента данной смеси газов в [долях]

M_см — среднюю молекулярную массу смеси [ кг / кмоль ] ф.8

ρ_см — плотность газа данного состава в С.У и Н.У [кг/м 3 ]

Δ_г — относительную плотность газа данного состава

Оформить в виде таблицы:

Массовый состав G_i

Внизу таблицы — среднюю М_см, ρ_см и Δ_г

Практическое занятие 6

Расчет приведенных параметров газа и его свойств в пластовых условиях

Для реальных газов, чтобы связать параметры состояния P, V и T, требуется вводить большое количество констант. Например, в зависимость P от V входят 5 констант, каждая из которых зависит от температуры. Поэтому имеется большое количество уравнений состояния, не достаточно точных, зато компактных, имеющих только 3 константы — например уравнение Ван-дер-Ваальса.

Экспериментально было показано, что для реальных газов в уравнение Менделеева- Клапейрона надо ввести коэффициент z

PV=znRT или PV=z T

который называется коэффициентом сверхсжимаемости газа и имеет смысл отклонения объема реального газа от идеального z=Vр/V идеального. Для идеального газа z=1

Коэффициент сверхсжимаемости является функцией приведенных давлений и температур: z = (P_пр, T_пр).

Приведенными параметрами индивидуальных газов называются безразмерные величины, показывающие во сколько раз действительные параметры состояния газа больше или меньше критических.

Приведенные параметры для смеси газов определяются по аналогич ным формулам , где вместо P_кр, T_кр, V_кр подставляют среднекритические значения для смеси P_кр.см, V_кр.см, T_кр.см, z_кр.см, которые в свою очередь вычисляются по правилу аддитивности

Источник

Газовые смеси способы выражения состава смесей

Для того чтобы воспользоваться уравнением Менделеева-Клапейрона для смеси газов

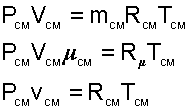необходимо знать газовую постоянную R_СМ и молярную массу (условную) смеси µ_СМ. Для смеси, как для любого идеального газа, эти две величины связаны соотношением R_СМ=8314/µ_СМ (Дж/(кг•К)). Чтобы рассчитать эти величины, необходимо знать состав смеси газов, т.е. какие газы и в какой пропорции входят в смесь.

Состав смеси может быть задан массовыми, объемными или мольными долями.

Массовой долей g_i данного газа называется отношение его массы к массе всей смеси:

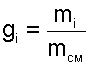где m_i – масса отдельного газа, входящего в смесь;
m_СМ – общая масса смеси.

Очевидно, что сумма массовых долей всех газов смеси равна единице:

Объeмной долей r_i данного газа называется отношение объема, который занимал бы данный газ при температуре и давлении смеси, к общему объему смеси:

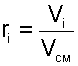где V_i – объем данного газа при Т_СМ и Р_СМ, м 3 .

Объем V_i называют парциальным объемом, это искусственно введенная величина, поскольку каждый газ, входящий в смесь, занимает весь объем смеси. Парциальный объем можно рассчитать по уравнению Менделеева – Клапейрона:

Записав уравнение Менделеева – Клапейрона через парциальное давление и через парциальный объем,

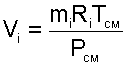можно получить еще одно расчетное выражение для объемной доли, поделив правые и левые части этих уравнений одно на другое:

Поскольку сумма парциальных давлений равна давлению смеси, то сумма объемных долей всех газов смеси равна единице, а сумма парциальных объемов равна полному объему всей смеси газов:

Для смеси газов используется понятие мольных долей. Мольной долей называется отношение количества молей данного газа М_i к общему количеству молей всех газов смеси М_СМ.

Количество молей определяется делением массы газа на его молярную массу:

Воспользовавшись уравнением Менделеева – Клапейрона для парциального и полного объемов смеси газов и введя в него количество молей

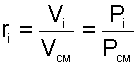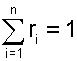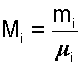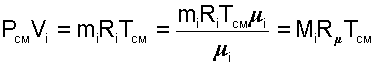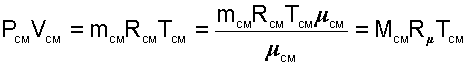получим еще одно расчетное выражение для мольной доли:

Равенство объемных и мольных долей для смеси газов можно получить и из закона Авогадро, в соответствии с которым объемы молей всех идеальных газов при одинаковых параметрах одинаковы, т.е. число молей при одинаковых параметрах идеальных газов прямо пропорционально полным объемам этих газов: V_{μ i}=V_i/М_i=V_СМ/М_СМ=V_{μ СМ}.

Существует взаимосвязь массовых и объемных долей смеси. Ее несложно получить, выразив массы газов через произведение их объемов на плотности, а отношение плотностей при одинаковых параметрах, в соответствии с законом Авогадро, заменив отношением молярных масс:

Уравнение (4.76) позволяет получить расчетные выражения для молярной массы и газовой постоянной смеси газов на основании равенства единице суммы массовых и объемных долей всех газов данной смеси:

При известной молярной массе смеси газовую постоянную смеси проще определить из соотношения

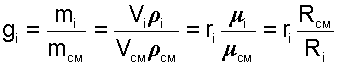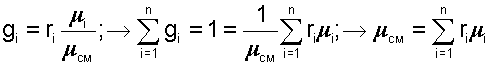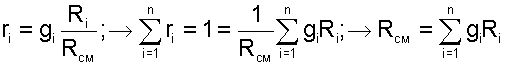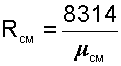Для определения парциального давления данного газа в смеси можно воспользоваться выражением (4.71). В соответствии с ним

Источник

Способы выражения состава

Нефтяной газ представлен в виде смеси углеводородов и неуглеводородных компонентов, поэтому для оценки его физико-химических свойств необходимо знать способы выражения состава смеси.

Массовая доля, весовой состав(g_i) i-го компонента – величина, нормированная на 1 в долях или на 100 %. Она характеризует отношение массы i-го компонента (m_i) в системе к общей массе системы:

(2.13)

Молярная доля, мольный состав (N_i) i-го компонента – величина, нормированная на 1 в долях или на 100 %, характеризует отношение числа молей i-го компонента (n_i) к общему числу молей компонентов в системе:

, (2.14)

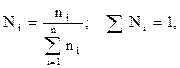
где m_i – масса i-го компонента;

М_i – молекулярный вес i-го компонента.

Из соотношений (2.13–2.14) легко вывести выражения для пересчётов массового и мольного составов:

[u9] . (2.15)

Объёмная доля i-го компонента – величина, нормированная на 1 или на 100 %, характеризует долю (V_i), которую занимает компонент в объёме системы. С учётом выражений (2.13–2.15) можно показать взаимосвязь объёмной доли с массовой и мольной долями:

. (2.16)

Для идеального газа соблюдается соотношение – объёмная доля компонента (V_i) равна мольной доли компонента (N_i) → V_i = N_i. Этот постулат есть следствие закона Авогадро.

Нефтяной газ рассматривается как идеальная система и его состав можно рассчитать на основе любых данных: масс компонентов, объёмов, плотностей, парциальных давлений и других величин.

Рассмотрим пример.

Дан объёмный состав нефтяного газа (V_i, %): CH₄ – 61,3 %;

Найти: какой будет массовый состав (g_i, в долях) газа?

Решение. Для идеального газа величины объёмных (V_i) и мольных (N_i) долей равны. Для расчета состава газа в массовых долях воспользуемся выражением (2.6).

Учитывая молекулярные массы (г/моль) компонентов нефтяного газа: CH₄ – 16; C₂H₆ – 30; C₃H₈ – 44; C₄H₁₀ – 58; C₅H₁₂ – 72, находим: g_CH4 = 61,3·16/(61,3·16 + 15,4·30 + 12,1·44 + 6,8·58 + 4,4·72) =

Сумма всех долей массового состава равна 1.

Уравнение состояния

Для определения многих физических свойств природных газов используется уравнение состояния.

Уравнением состояния называется аналитическая зависимость между параметрами, описывающими изменение состояние вещества. В качестве таких параметров используются давление, температура, объём.Состояние газа при нормальных и стандартных условиях описывается уравнением Менделеева–Клапейрона:

, (2.17)

где Р – абсолютное давление, Па;

Q – количество вещества, моль;

Т – абсолютная температура, К;

R – универсальная газовая постоянная, Па×м 3 /(моль×град).

На основе уравнения состояния газа можно рассчитывать многие параметры нефтяного газа: плотность, мольный объём, количество молекул, число молекул, парциальные давления и другие, если рассматривать количество вещества в уравнении состояния газа (2.17), равное 1 молю (Q = 1 моль).

С учётом этого, уравнение состояния газа можно преобразовать следующим образом:

Если сумма молей равна единице (∑N = 1 моль), следует, что уравнение приобретает вид Þ Р·V = R·T.

Зная, что масса (m) одного моля идеального газа равна его молекулярной массе (М), умножив левую и правую части на молекулярную массу и массу газа, соответственно, получим:

Поделив обе части на V·R·T и преобразовав (2.19), получим выражение для расчёта плотности:

Р·M/R·T = m/V, m/V = M·Р/R·T, r = M·Р/R·T. (2.20)

Рассмотрим пример.

Дан один моль метана CH₄.

Найти: какова будет плотность метана при н.у. и с.у.?

Решение. Зная, что молекулярная масса метана равна 16,04 г/моль и один моль метана занимает объём при н.у. 22,414 л, а при с.у. 24,055 л, находим:

Из выражения (2.20) и расчётов следует, что плотность газа с возрастанием давления будет расти, а с возрастанием температуры уменьшаться.

Плотность смеси газовых компонентов рассчитывают с учётом средней молекулярной массы смеси газа (M_см) как отношение молекулярной массы смеси газа к его мольному объёму (V_м).

Например, для нормальных условий плотность газа будет рассчитываться по выражению:

Если плотность газа (ρ_о) задана при атмосферном давлении, равном 0,1013 МПа, то пересчёт её величины с учётом другого давления (Р) при той же температуре для идеального газа выполняется по формуле:

Рассмотрим другой пример.

Плотность метана при н.у. равна 0,716кг/м 3 . Определить плотность метана (СН₄) при избыточном давлении, например при давлении 500 кПа и температуре 0 °С.

Решение. В этом случае общее давление (1 атм = 101,325 кПа) в системе будет равно Р = (500 + 101,325) = 601,325 кПа.

Зная, что молекулярная масса метана = 16,04 г/моль (кг/кмоль), универсальная газовая постоянная (R) = 8,314 Дж/(К·моль), температура (T) = 273,15 К, находим плотность метана по (2.20 и 2.22):

r_CH4 = Р·М/R·T = 601,325·16,04/8,314·273,15 = 4,25 (кг/м 3 ),

Относительная плотность газов величина, рассчитанная по отношению к плотности воздуха, определенного при тех же условиях:

Плотность воздуха (ρ_возд) при н.у. равна » 1,293 кг/м 3 , а при с.у. » 1,189 кг/м 3 .

Рассмотрим пример.

Для условий задачи, рассмотренной выше (пример раздела 2.2), рассчитать абсолютные (r) и относительные (ρ о _см) плотности смеси газов, используя правое выражение (2.12) для расчета молекулярной массы (г/моль):

М_см = 100/(36,5/16 +17,2/30 +19,8/44 +14,7/58 +11,8/72) = 26,874;

r_см = 26,874/22,414 = 1,119 (кг/м 3 );

ρ о _см (н.у.) = 1,119/1,293 = 0,927.

Аналогично из (2.20) находится и выражение для мольного объёма:

Мольный объём при давлениях, равных или близких атмосферному и, для физических процессов, когда не происходит изменения числа молей в системе, оценивается соотношением:

где R – универсальна газовая постоянная;

Т – температура, К.

Рассмотрим пример.

Найти вид зависимости изменения мольного объёма газа от температуры → V = f(T).

Решение. Воспользуемся выражением (2.25) и получим объём, занимаемый одним молем идеального газа для условий задачи:

V_н.у. = 0,08206·273,15 = 22,414 (м 3 ,);

V_с.у. = 0,08206·293,15 = 24,055 (м 3 ).

Любой газ при н.у. (Т = 0 о С и Р = 100 кПа, 760 мм рт. ст.) занимает объём, равный 22,414 м 3 , а при с.у. (Т = 20 о С и Р = 100 кПа) занимает объём равен 24,055 м 3 .

С увеличением температуры мольный объём газа увеличивается. Мольный объём газов с возрастанием температуры будет расти, а с возрастанием давления уменьшаться(2.24).

У этого уравнения есть свои граничные условия. Оно справедливо для описания поведения газов при давлениях, близких к атмосферному (от 0,1 до 1,0–1,2 МПа), и при температурах ≈ 0–20 о С. При повышенном давлении газ сжимается и его состояние отличается от поведения идеальных газов.

Источник