Функция способы задания функции четность нечетность периодичность

Основные свойства функции: четность, нечетность, периодичность, ограниченность.

Функция — это одно из важнейших математических понятий. Функция — зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x) образуют область определения функции. Все значения, которые принимает зависимая переменная (переменная y), образуют область значений функции.

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x, а по оси ординат откладываются значения переменной y. Для построения графика функции необходимо знать свойства функции. Основные свойства функции будут рассмотрены далее!

Для построения графика функции советуем использовать нашу программу — Построение графиков функций онлайн. Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме. Также на форуме Вам помогут решить задачи по математике, химии, геометрии, теории вероятности и многим другим предметам!

Основные свойства функций.

1) Область определения функции и область значений функции.

Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y, которые принимает функция.

В элементарной математике изучаются функции только на множестве действительных чисел.

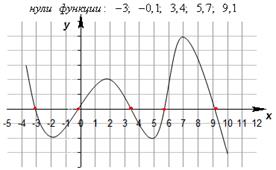
2) Нули функции.

Значения х, при которых y=0, называется нулями функции. Это абсциссы точек пересечения графика функции с осью Ох.

3) Промежутки знакопостоянства функции.

Промежутки знакопостоянства функции – такие промежутки значений x, на которых значения функции y либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.

4) Монотонность функции.

Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

5) Четность (нечетность) функции.

Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого хиз области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любогох из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.

Четная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
2) Для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.

Нечетная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
2) для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=-f(x)
3) График нечетной функции симметричен относительно начала координат (0; 0).

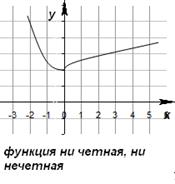
Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.

6) Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.

7) Периодическость функции.

Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

Функция f называется периодической, если существует такое число , что при любом x из области определения выполняется равенство f(x)=f(x-T)=f(x+T). T — это период функции.

Всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.

Значения периодической функции через промежуток, равный периоду, повторяются. Это используют при построении графиков.

Источник

Четность и нечетность функции. Период функции. Экстремумы функции

Содержание

Способы задания функции

Пусть функция задается формулой: y=2x^<2>-3 . Назначая любые значения независимой переменной x , можно вычислить, пользуясь данной формулой соответствующие значения зависимой переменной y . Например, если x=-0,5 , то, пользуясь формулой, получаем, что соответствующее значение y равно y=2 \cdot (-0,5)^<2>-3=-2,5 .

Взяв любое значение, принимаемое аргументом x в формуле y=2x^<2>-3 , можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:

x	−2	−1	0	1	2	3
y	−4	−3	−2	−1	0	1

Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.

Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.

Четная и нечетная функция

Функция является четной функцией, когда f(-x)=f(x) для любого x из области определения. Такая функция будет симметрична относительно оси Oy .

Функция является нечетной функцией, когда f(-x)=-f(x) для любого x из области определения. Такая функция будет симметрична относительно начала координат O (0;0) .

Функция является ни четной, ни нечетной и называется функцией общего вида, когда она не обладает симметрией относительно оси или начала координат.

Исследуем на четность нижеприведенную функцию:

D(f)=(-\infty ; +\infty ) с симметричной областью определения относительно начала координат. f(-x)= 3 \cdot (-x)^<3>-7 \cdot (-x)^<7>= -3x^<3>+7x^<7>= -(3x^<3>-7x^<7>)= -f(x) .

Значит, функция f(x)=3x^<3>-7x^ <7>является нечетной.

Периодическая функция

Функция y=f(x) , в области определения которой для любого x выполняется равенство f(x+T)=f(x-T)=f(x) , называется периодической функцией с периодом T \neq 0 .

Повторение графика функции на любом отрезке оси абсцисс, который имеет длину T .

Промежутки, где функция положительная, то есть f(x) > 0 — отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих выше оси абсцисс.

f(x) > 0 на (x_<1>; x_<2>) \cup (x_<3>; +\infty )

Промежутки, где функция отрицательная, то есть f(x) — отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.

f(x) на (-\infty; x_ <1>) \cup (x_<2>; x_ <3>)

Ограниченность функции

Ограниченной снизу принято называть функцию y=f(x), x \in X тогда, когда существует такое число A , для которого выполняется неравенство f(x) \geq A для любого x \in X .

Пример ограниченной снизу функции: y=\sqrt<1+x^<2>> так как y=\sqrt<1+x^<2>> \geq 1 для любого x .

Ограниченной сверху называется функция y=f(x), x \in X тогда, когда существует такое число B , для которого выполняется неравенство f(x) \neq B для любого x \in X .

Пример ограниченной снизу функции: y=\sqrt<1-x^<2>>, x \in [-1;1] так как y=\sqrt<1+x^<2>> \neq 1 для любого x \in [-1;1] .

Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .

Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .

Возрастающая и убывающая функция

О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_ <1>и x_ <2>, причем x_ <1>> x_ <2>, будет y(x_<1>) > y(x_<2>) .

Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_ <1>и x_ <2>, причем x_ <1>> x_ <2>, будет y(x_<1>) .

Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0 ).

а) Если при x > 0 четная функция возрастает, то убывает она при x

б) Когда при x > 0 четная функция убывает, то возрастает она при x

в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x

г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x

Экстремумы функции

Точкой минимума функции y=f(x) принято называть такую точку x=x_ <0>, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_ <0>), и для них тогда будет выполняться неравенство f(x) > f(x_<0>) . y_ — обозначение функции в точке min.

Точкой максимума функции y=f(x) принято называть такую точку x=x_ <0>, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_ <0>), и для них тогда будет выполняется неравенство f(x) . y_ — обозначение функции в точке max.

Необходимое условие

Согласно теореме Ферма: f'(x)=0 тогда, когда у функции f(x) , что дифференцируема в точке x_ <0>, появится экстремум в этой точке.

Достаточное условие

1. Когда у производной знак меняется с плюса на минус, то x_ <0>будет точкой минимума;
2. x_ <0>— будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_ <0>.

Наибольшее и наименьшее значение функции на промежутке

1. Ищется производная f'(x) ;
2. Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку [a; b] ;
3. Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции, а большее — наибольшим.

Источник

Материал к уроку «Четные и нечетные функции»

Четность и нечетность функции

Функция называется четной , если для любого значения х из ее области определения значение – х также принадлежит области определения и верно равенство f ( ‑ x )= f ( x ).

Область определения четной функции симметрична относительно нуля.

График четной функции симметричен относительно оси Оу .

Функция называется не четной , если для любого значения х из ее области определения значение – х также принадлежит области определения и верно равенство f ( ‑ x )= ‑ f ( x ).

Область определения нечетной функции симметрична относительно нуля.

График нечетной функции симметричен относительно начала координат.

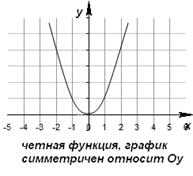
Пример 1 . Дан график функции .

Определите по графику четной или нечетной является функция.

Решение . Поскольку график функции симметричен относительно оси Ох , то функция является четной.

Ответ : функция четная

Задание 1 . Определите по графику четной или нечетной является функция…

1)

2)

3)

4 )

5 )

6 )

7)

8)

9)

10)

Пример 2. На рисунке изображена часть графика некоторой функции, область определения которой — промежуток [ ‑ 4; 4] . Постройте график этой функции, если функция нечетная.

Решение . График нечетной функции симметричен относительно начала координат.

Следовательно, для построения графика нужно отобразить данную часть относительно точки (0; 0):

Задание 2. На рисунке изображена часть графика некоторой функции, область определения которой — промежуток [ ‑ 3; 3] . Постройте график этой функции, если…

1) функция четная

2) функция нечетная

3) функция четная

4) функция нечетная

5) функция четная

6) функция нечетная

7) функция четная

8) функция нечетная

9) функция четная

10) функция нечетная

Пример 3 . Определить четность (нечетность) функции .

Решение . По определению четной функции должно выполняться равенство f ( ‑ x )= f ( x ).

= . Отсюда следует, что функция четная.

Ответ : четная

Задание 3. Определите, является функция четной, нечетной или не является ни четной, ни нечетной…

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

Пример 4. Исследовать функцию на четность (нечетность).

Решение . Подставим в выражение вместо х значение ‑ х : = = . Отсюда следует, что функция нечетная.

Ответ : нечетная

Задание 4. Определите четность или нечетность функции…

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

Пример 5. Вычислите , если f ( x ) – нечетная функция и f ( ‑ 5)=3; f (2)= ‑ 8.

Решение . Поскольку функция f ( x ) – нечетная, то f ( ‑ x )= ‑ f ( x ).

Следовательно, =4( ‑ 3)+8= ‑ 4.

Ответ : ‑ 4

Задание 5 . Вычислите…

1) , если f ( x ) – нечетная функция и f (3)= ‑ 7; f ( ‑ 4)=3

2) , если f ( x ) – четная функция и f (2)=3; f ( ‑ 5)=2

3) , если f ( x ) – четная функция и f (3)= ‑ 7; f ( ‑ 4)=5

4) , если f ( x ) – нечетная функция и f ( ‑ 4)=2; f (2)= ‑ 3

5) , если f ( x ) – нечетная функция и f ( ‑ 3)=1; f (2)= ‑ 3

6) , если f ( x ) – четная функция и f (2)=2; f ( ‑ 3)=3

7) , если f ( x ) – четная функция и f (3)=3; f (5)=2

8) , если f ( x ) – нечетная функция и f ( ‑ 4)=3; f (3)=5

9) , если f ( x ) – нечетная функция и f ( ‑ 3)=3; f (2)= ‑ 3

10) , если f ( x ) – четная функция и f ( ‑ 2)=3; f ( ‑ 5)=4

Сумма двух четных функций четна, а сумма двух нечетных – нечетна.

Произведение двух четных функций является четной функций, произведение двух нечетных функций также является четной функций. Произведение четной и нечетной функции – нечетно.

Если функция f четна (нечетна), то и функция четна (нечетна).

Доказательство : если функция f четна и f ( x )  0, то .

Если Х симметрично относительно начала координат, то любая заданная на Х функция f является суммой четной и нечетной функций f = g + h , где , .

Доказательство : , . Отсюда следует, что функция g ( x ) четна, а функция h ( x ) нечетна. При этом .

Пример 6 . Функции f и g определены на множестве всех действительных чисел. Является ли функция h четной или нечетной, если h ( x )= f 2 ( x ) g 2 ( x ), f – четная функция, g – нечетная?

Решение . Поскольку f – четная функция, g – нечетная, то f 2 и g 2 – четные функции. Произведение четных функций – функция четная. Следовательно, h ( x )= f 2 ( x ) g 2 ( x ) является четной функцией.

Ответ : четная

Задание 6. Функции f и g определены на множестве всех действительных чисел. Является ли функция h четной или нечетной, если…

f – четная функция, g – нечетная

f и g – четные функции

f и g – нечетные функции

Источник