Функция отображения способы задания функции

3. Отображение и функции

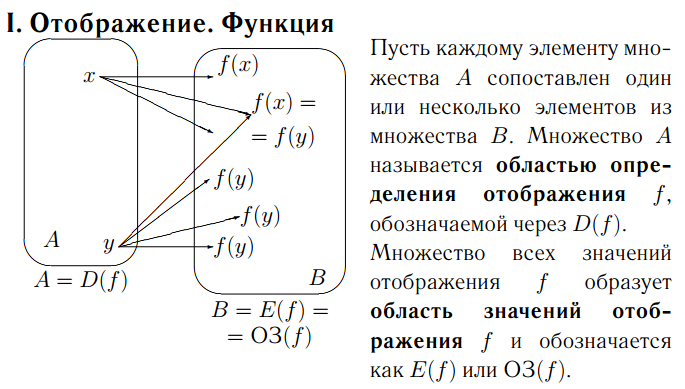
1) Определение. Соответствие, при котором каждому из элементов множества X сопоставляется единственный элемент из множества Y, называется отображением.

3) Если элементу x соответствует y, то y называется образом элемента x, а x —прообразом элемента y. Пишут: или y = f(x). Множество A всех элементов , имеющих один и тот же образ , называется полным прообразом элемента y.

4) Область определения функции — это все значения x, при которых существует функция.Другими словами, область определения функции, заданной формулой, является все значения аргумента, за исключением тех, которые приводят к действиям, которые мы не можем выполнить. На данный момент мы знаем только два таких действия. Мы не можем делить на нуль и не можем извлечь квадратный корень из отрицательного числа.

5)Способы задания, виды и св-ва отображений

ВЫРАЖЕНИЕ или ФОРМУЛА. Переменная, вместо которой надо подставлять элемент из области определения, называется аргументом функции. При этом явно указывается процедура вычисления значения f(x) функции f на аргументе x, точнее, при любом значении аргумента. Фактически этим способом мы указываем правило вычисления значения функции f при произвольном значении аргумента x.ТАБЛИЦА. Таблица значений функции состоит, как правило, из двух строк. В первой строке перечисляются все (!) элементы области определения, а во второй строке — соответствующие им значения функции.

ГРАФИК.Графиком функции f называется множество точек плоскости с координатами x, f(x) .

6)Операции над отображениями

1. Обращение y:A→B Y(x)=y

Композиция y1*y2 отображение y1:a->c,такая что y(x)=y1*y2(x)=Z(ЕyϵB)(y1=y1(x)&y2(y)=Z)

7)Ф-ии как спец класс отображений

8)Классификация ф-ий по типу мн-в

3.Бинарные отношения

1)Отношение

2) Бинарным отношениемназывается двухместное отношение между любыми двумя множествамиA и B, т.е. всякое подмножество декартова произведения этих множеств:  A B .

3)примеры Примеры бинарных отношений:

на множестве целых чисел отношения «делится», «делит», «равно», «больше», «меньше», «взаимно просты»;

на множестве прямых пространства отношения «параллельны», «взаимно перпендикулярны», «скрещиваются», «пересекаются», «совпадают»;

на множестве окружностей плоскости «пересекаются», «касаются», «концентричны».

4)Способы задания

5) св-ва бинарных отношений

6) Проекция элемента (a, b) множества Ах В на множество А есть элемент а. Аналогично, элемент b является проекцией элемента (a, b) множества Ах В на множество В. Проекцией множества Е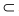Ах В на А называется множество всех тех элементов из А, которые являются проекциями элементов из Е на множество А

7) Срез бинарного отношения. Различают срез бинарного отношения через элемент и через подмножество первого базисного множества.

8)Факториалы

9)Отношение эквивалентности

10) связь с разбиениями

11) Бинарное отношение ť на мн-ве A(ť AxA) наз-ся отношением толерантности, если оно рефлексивно и симметрично.

12) его связь с покрытием

13) отношение порядка

14) стр-ра упорядоченных мн-в

15) Решётка — частично упорядоченное множество, в котором каждое двухэлементное подмножество имеет как точную верхнюю (sup), так и точную нижнюю (inf) грани. Отсюда вытекает существование этих граней для любых непустых конечных подмножеств.Решётка может быть также определена как универсальная алгебра с двумя бинарными операциями (они обозначаются \/и /\ или + и ∙)

Источник

Функции, отображения, отношения

Основные понятия

Пусть даны два множества и . Тогда пары (a_i, b_i) задают соответствие между множествами А и В, если указано правило R, по которому для элемента a_i множества А выбирается элемент b_i из множества В.

Например, соответствие между элементами множеств и задаёт точечное множество (х_i; у_i) координат точек на плоскости.

Пусть задано соответствие R и Y= R(Х). Ему соответствует точка M с координатами (х; у). Тогда множество точек плоскости, выделяемое отображением R, будет графиком.

Задание отображений

Для описания соответствий между множествами используют понятие отображения (функции) одного множества на другое.

Для задания отображения необходимо указать:

­ множество, которое отображается (область определения данного отображения, часто обозначается );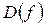

­ множество, в (на) которое отображается данная область определения (множество значений этого отображения, часто обозначается );

­ закон или соответствие между этими множествами, по которому для элементов первого множества (прообразов, аргументов) выбраны элементы (образы) из второго множества. Приняты записи или .

Везде при записи будем подразумевать, что отображение f определено всюду на А, т.е А – полный прообраз отображения f, хотя для В такого свойства полноты подразумевать не будем. Запись f(А) означает, что это множество состоит из образов всех элементов множества А: f(А):= <f(a) |aÎA>. Очевидно, что . Далее будем иметь дело в основном с однозначнымиотображениями, где каждому аргументу поставлено в соответствие не более одного образа.

Отображения задаются аналитически, таблично, графически.

Способ задания отображения в виде формул называется аналитическим.

Для задания отображения множеств табличным способом принято строить таблицу, в которой первую строку составляют элементы области определения (прообразы вида a), а вторую строку – их образы f(a).

Графическоепредставление отображения связано со стрелочными схемами (диаграммами или графами), которые подробно рассматриваются в главе 2.

Понятие «функция» является одним из основных в математике. В данном случае подразумевается прежде всего функция, отображающая одно конечное множество объектов в другое конечное множество. Поэтому по смыслу термин «отображение» и «функция» почти идентичны.

Виды отображений

Различают два основных вида однозначных отображений (функций). По мощности они делятся на сюръективные и инъективные.

Сюръекция – соответствие, при котором каждому элементу множества А указан единственный элемент множества В, а каждому элементу множества В можно указать хотя бы один элемент множества А, называется отображением множества А на множество В.

Инъекция – соответствие, при котором каждому элементу множества А соответствует единственный элемент множества В, а каждому элементу В соответствует не более одного прообраза из А, называется отображением множества А вомножество В.

Биекцией называется отображение множества А на множество В, при котором каждому элементу множества В соответствует единственный элемент множества А, является взаимно-однозначным соответствием между двумя множествами. На рис. 1.10 изображены отображения .

Пусть множество А отображается взаимно-однозначнона множество В, т.е . Тогда отображение f –1 , при котором каждому элементу множества В ставится в соответствие его прообраз из множества А, называется обратным отображением для f и записывается . Так как одному образу при биекции соответствует в точности один прообраз, обратное отображение будет определено всюду на В и однозначно.

Пусть А и В – два множества. Бинарным отношением R из множества А в множество В называется подмножество прямого (декартова) произведения А и В: . Для бинарных отношений используется следующая форма записи:

.

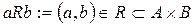
Если А= В, то R есть отношение на множестве А.

Отношения являются частным случаем отображения, когда область определения и множество значений совпадают, поэтому всё сказанное в п. 1.4 справедливо и для отношений.

Назовём n –местным отношением R на непустом множестве М, это подмножество . При отношение R называется бинарным. То есть бинарнымотношением между элементами множеств А и В называют любое подмножество R множества А×В.

Если отношение n – местное, то в общем случае можно записать

.

Множества А_i не обязательно различны, а отношение R – это множество упорядоченных кортежей .

Обратное отношение: .

Дополнение отношение .

Тождественное отношение: .

Композицией отношений R₁ и R₂ называется отношение, если

, , .

Свойства отношений

Приведем характерные свойства бинарных отношений, причём заметим, что каждое конкретное отношение может обладать или не обладать некоторыми из указанных свойств.

1. Рефлексивность: , например, «быть не больше» на R.

2. Антирефлексивность. Имеет место, когда отношение не обладает свойством 1 для любых а, например «быть больше», «быть младше» и др.

3. Симметричность любых двух элементов. Отношение R на множестве М называется симметричным, если для любых a, одновременно справедливо и (т.е. ). Симметрична параллельность прямых, так как если а||b, то b||а. Симметрично отношение «быть равным» на любом множестве или «быть взаимно простым» на N.

4. Антисимметричность. Если для несовпадающих элементов а≠b верно отношение , то ложно . Антисимметричными являются отношения «быть больше», «не меньше» на R, «быть делителем» на N и др.

5. Транзитивность. Если aRb и , то aRc для любых . Транзитивны отношения «быть больше», «быть параллельным», «быть равным» и др.

6. Антитранзитивность. Имеет место, когда отношение не обладает свойством 5. Например, «быть перпендикулярным» на множестве прямых плоскости ( , но неверно ).

7. Асимметричность. Ни для одной пары а и b не выполняется одновременно и .

8. Связность. Для любых а и b, если а≠b, то или . Некоторые свойства конкретных бинарных отношений приведены в таблице ниже.

Отношения эквивалентности

Различные отношения могут обладать (или не обладать) теми или иными свойствами, приведенными выше. Некоторые устойчивые комбинации этих свойств встречаются настолько часто, что их следует выделить отдельно. Классы отношений, обладающие определённым набором свойств можно изучить отдельно. К таким классам отношений относятся: отношения эквивалентности, толерантности, порядка.

Свойства бинарных отношений

Множес-тва	Отноше-ние	Рефлек-сивность	Симмет-ричность	Асиммет-ричность	Антисим-метричность	Транзи-тивность	Антитран-зитивность
Любые	AÌB	+	–	–	+	+	–
Любые непустые		+	+	–	–	–	–
Любые		–	+	–	–	–	–
Любые	а=b	+	+	–	–	+	–
Любые	а≠b	–	+	–	–	–	+
R	а>b	–	–	+	–	+	+
R	а³b	+	–	–	+	+	+
R	а есть отношения строгого полного порядка. Отношение Ì есть отношение нестрогого частичного порядка на множестве (булеан). Всякий частичный порядок на конечном множестве может быть доведён до полного. То есть существует такое отношение полного порядка, для которого заданное отношение частичного порядка является подмножеством. Источник Оцените статью Вам также может понравиться Ясень семена способ распространения Ясень обыкновенный Fraxinus excelsior – так в ботанической Ярлыки способы создания ярлыков ос windows Создаем ярлыки на рабочем столе Windows Создаем ярлыки Японское удобрение фуджима способ применения Удобрения Фуджима Знаете потрясающее удобрение, палочка Японский чай способ заварки Технология заваривания японского чая Известно, что Правообладателям Политика конфиденциальности Контакты