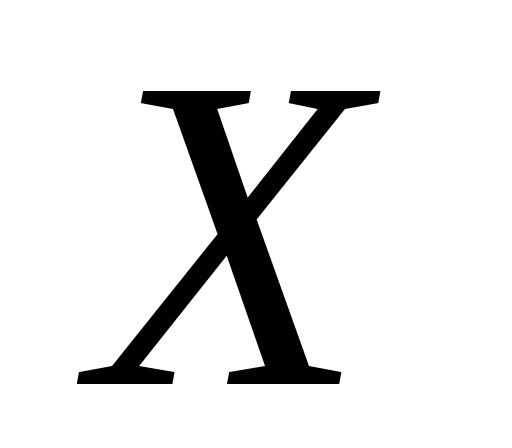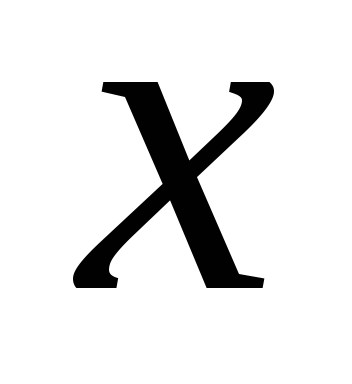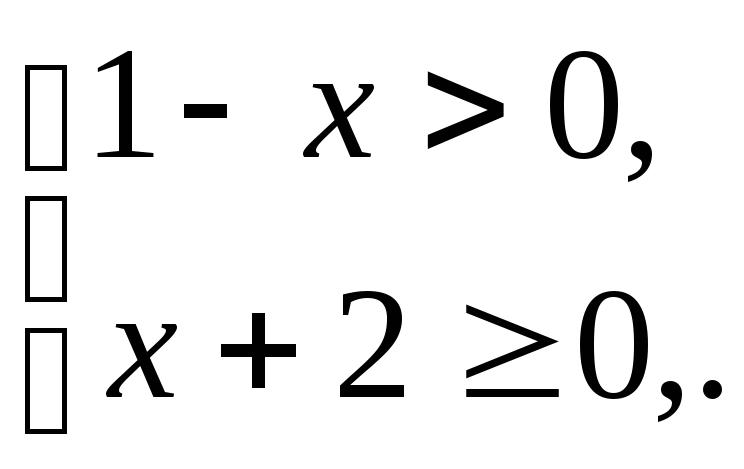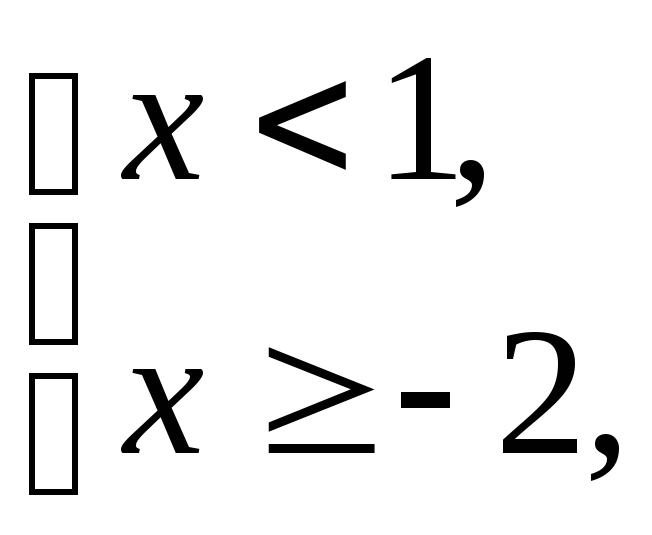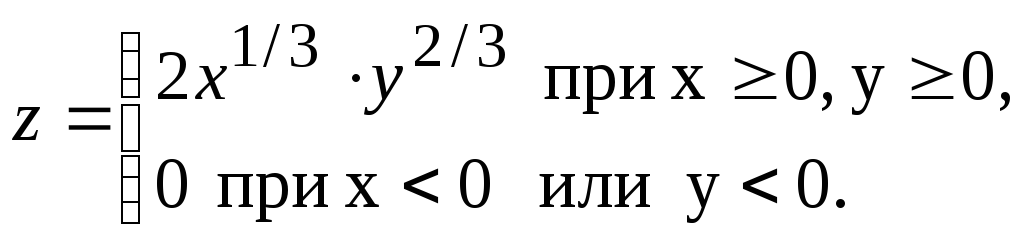Математика
Раздел «Математический анализ»
Модуль 1. дифференциальное исчисление функции одной переменной
Тема 1. Функции одной переменной, свойства и графики
Определение функций одной переменной.
Способы задания функций одной переменной.
Основные свойства функций.
Преобразования графиков функций
Тема 2. Предел и непрерывность функции одной переменной
Предел функции в точке и на бесконечности.
Основные свойства пределов.
Бесконечно малые и бесконечно большие функции.
Раскрытие неопределенностей 
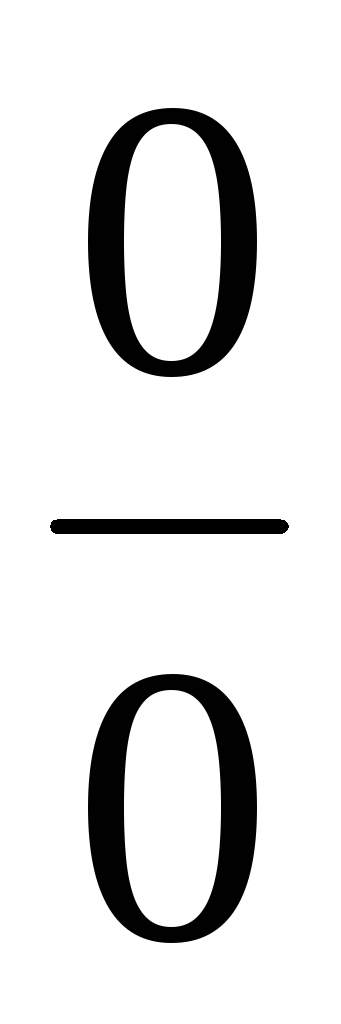
Первый и второй замечательные пределы
Эквивалентные бесконечно малые функции
Непрерывность функции, точки разрыва
Свойства функций, непрерывных на отрезке.
Тема 3. Производные и дифференциалы. Экстремумы функции одной переменной
Геометрический и экономический смысл производной.
Основные правила дифференцирования.
Таблица основных формул дифференцирования.
Производные высших порядков.
Вычисление пределов с помощью производных.
Свойства дифференциала функции.
Применение дифференциала к приближенным вычислениям.
Дифференциалы высших порядков
Экстремумы (максимумы и минимумы) функции.
Наименьшее и наибольшее значения непрерывной функции на отрезке.
Модуль 1. Дифференциальное исчисление функции одной переменной
Тема 1. Функции одной переменной, свойства и графики
Определение функций одной переменной.
Способы задания функций одной переменной.
Основные свойства функций.
Преобразования графиков функций.
Понятие функции применяется не только в математике, но и в других областях знаний. В философии функция (лат. function – исполнение) – обязанность, круг деятельности 1 .
Функцией в общественных науках обычно называют предназначение, роль какого-либо элемента в социальной системе, или, иными словами, определенного вида работу, которая требуется от него в интересах системы в целом.
В менеджменте функция означает исполнение, совершенствование, служебную обязанность, назначение, роль. В широком смысле «функция» — это устойчивый вид деятельности, то, что обязан выполнять сотрудник независимо от своего желания.
1. Определение функций одной переменной
Дадим определение функции одной переменной.
Функцией (отображением), заданной на множестве 
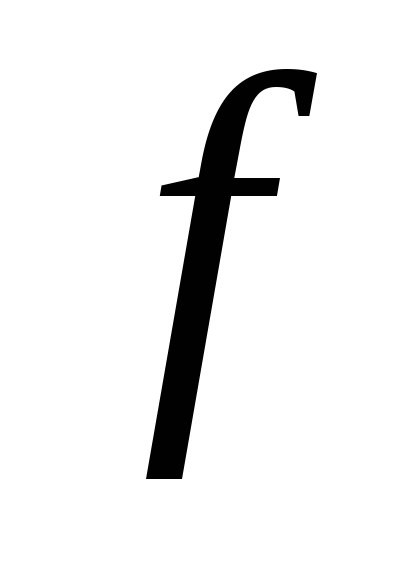

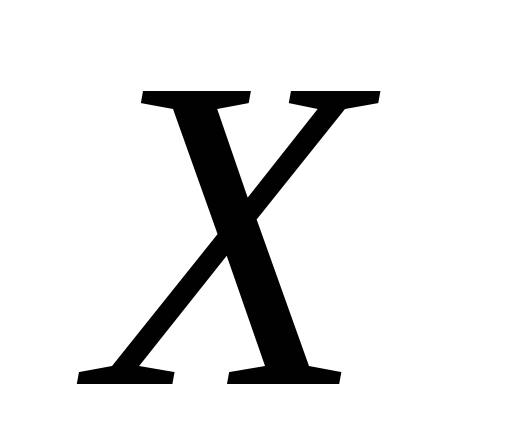


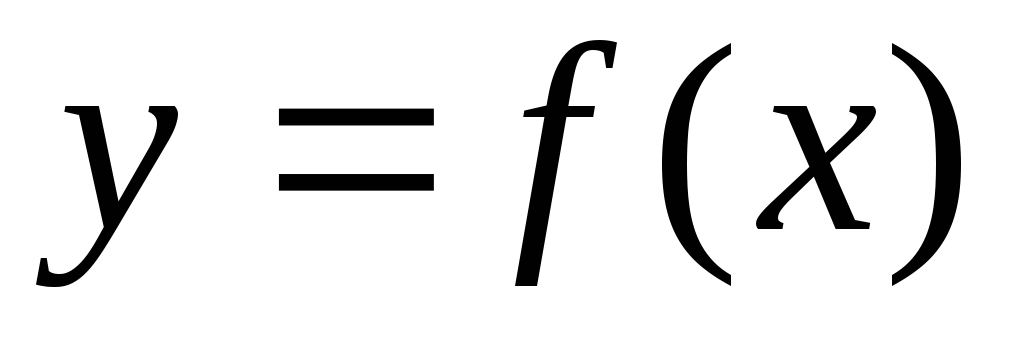
Множество 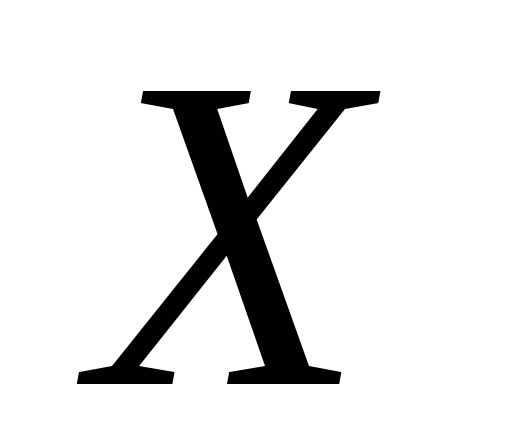


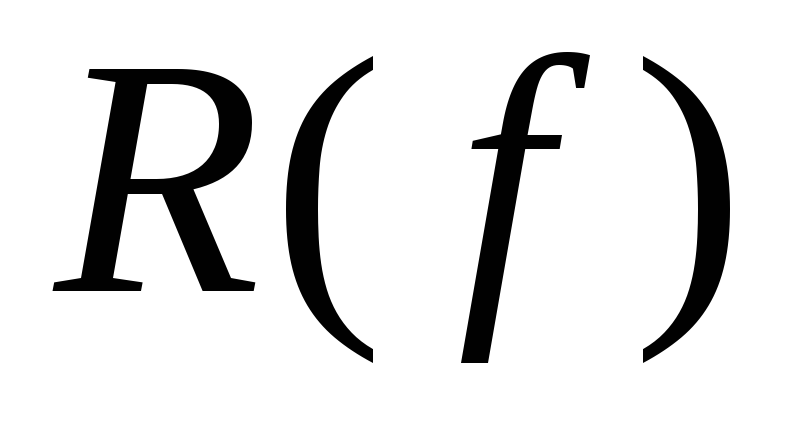
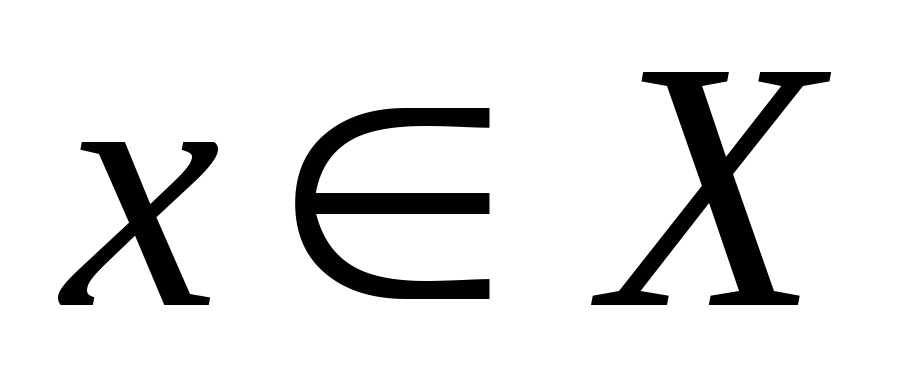

Если 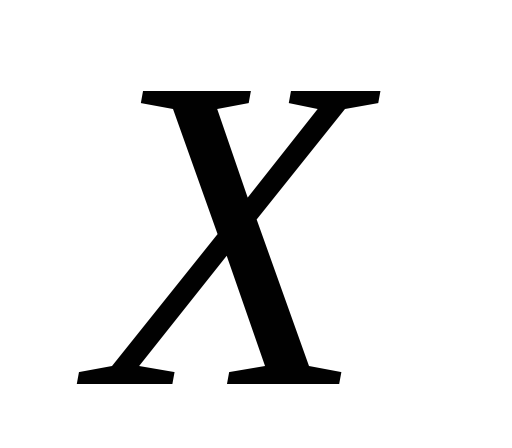


Рис. 1 – Математическое определение функции
Областью определения 





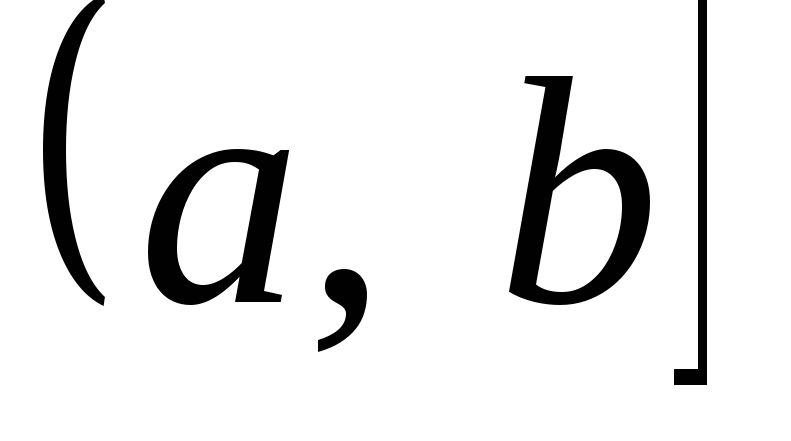
Пример 1. 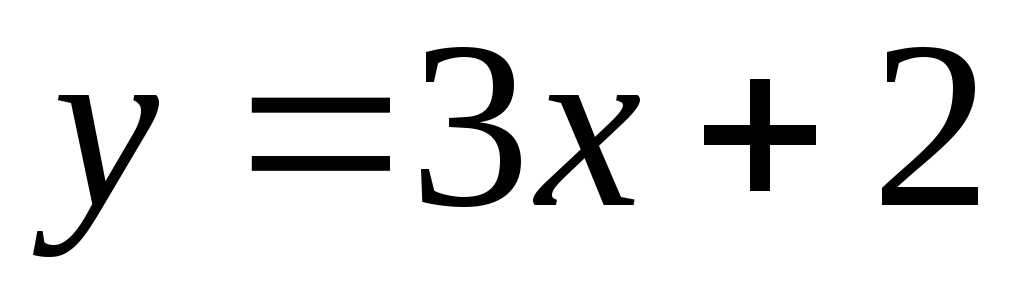
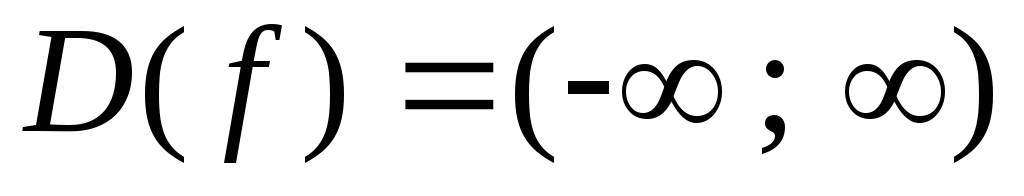
Пример 2. 

Пример 3. 
Решение. Так как 

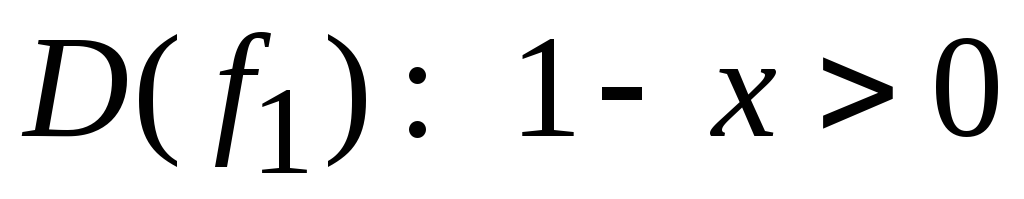
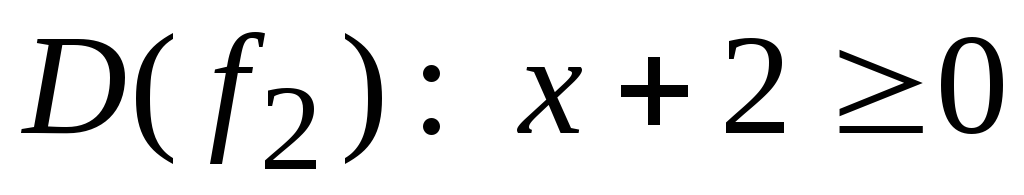
Тогда
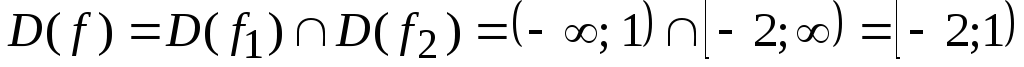
Основными способами задания функций являются аналитический, табличный, графический. Существует и другие способы задания функций — алгоритмический, с помощью программы на ЭВМ.
Аналитический способ задания функции – имеется формула, указывающая, какие действия нужно произвести над аргументами, чтобы получить значение функции. Аналитический способ может быть явным и неявным.
Функция задана явно, если она задана:
одной формулой, разрешенной относительно зависимой переменной (например, у =
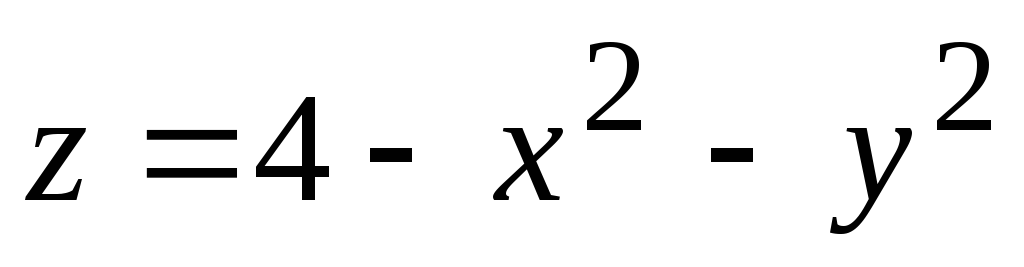
разными формулами на определенных числовых промежутках (кусочно-аналитическое задание функции): например, 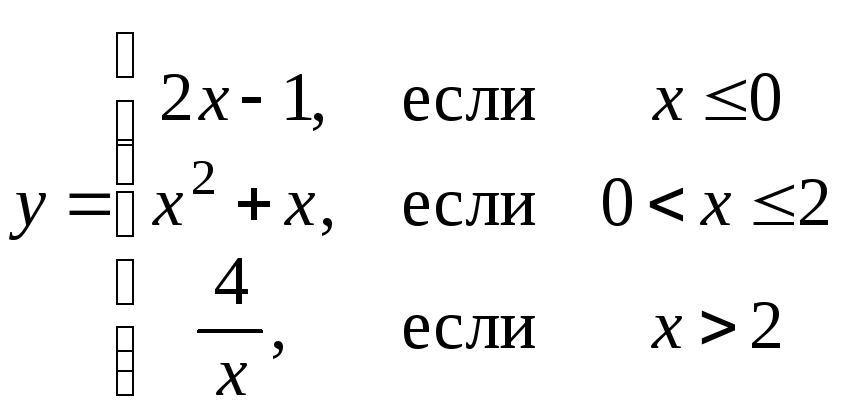
Пример 4. Вычислить значения функции 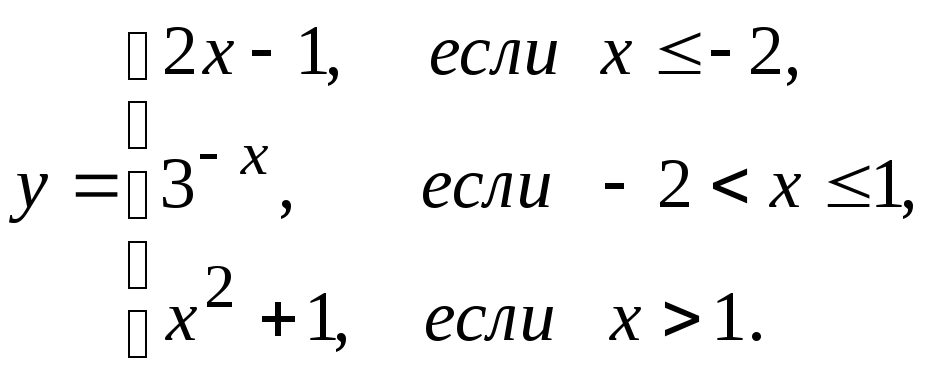
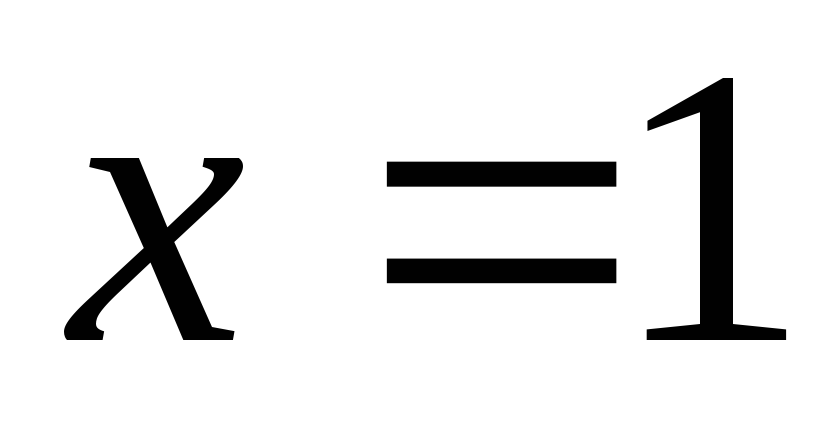
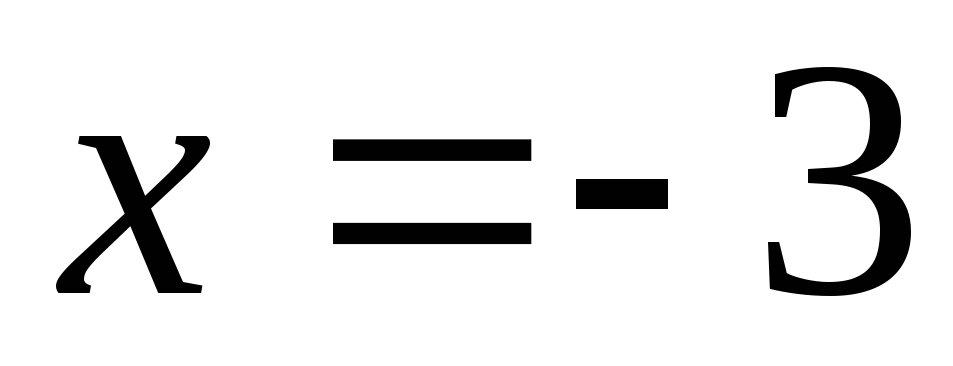

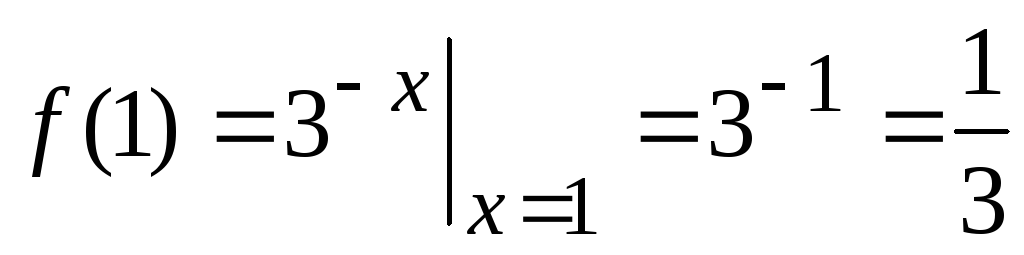
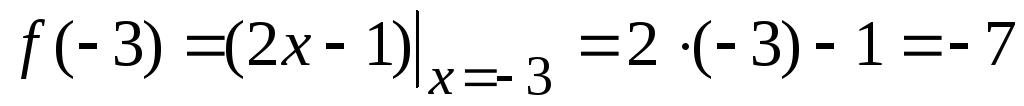
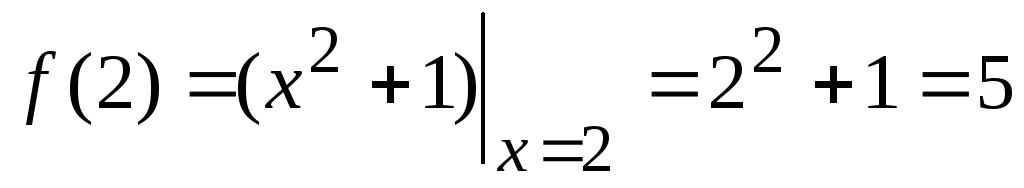
Функция одной или двух переменных называется неявной, если она задана уравнением, не разрешенной относительно зависимой переменной. Например, 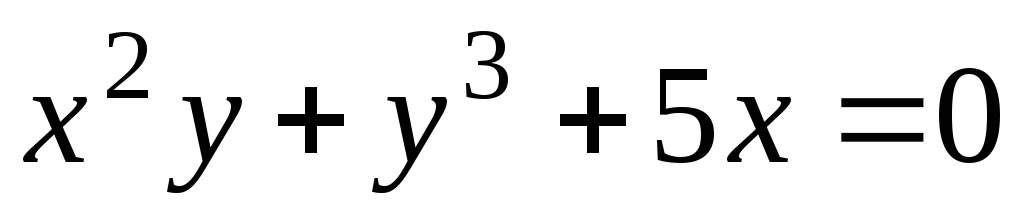
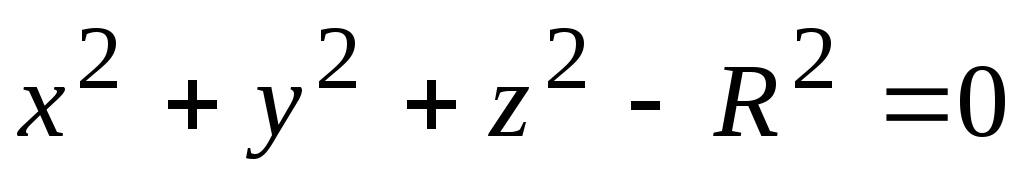
Табличный способ задания функции — с помощью таблицы, в которой указаны значения аргументов и соответствующие им значения зависимой переменной. Например, таблицы Брадиса.
Достоинством табличного способа является то, что по таблице можно непосредственно найти значение функции для имеющихся в таблице значений аргумента, а недостатком – отсутствие значений функции для промежуточных значений аргумента.
Таблица функции одной переменной
Графический способ задания функции.
Для функции одной переменной:
Графиком функции 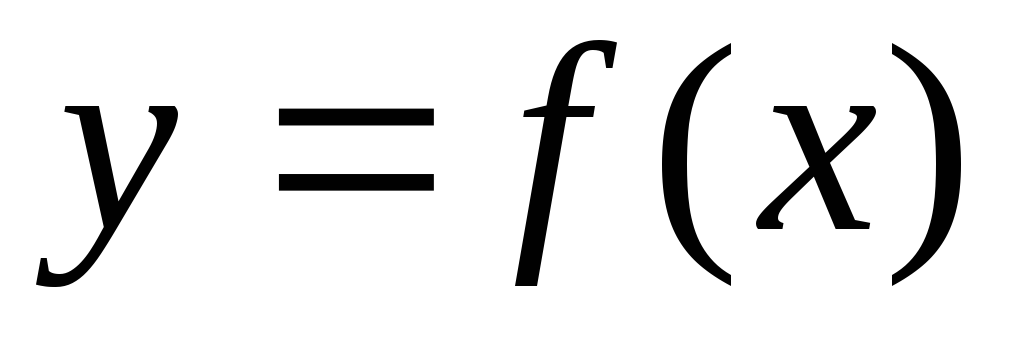
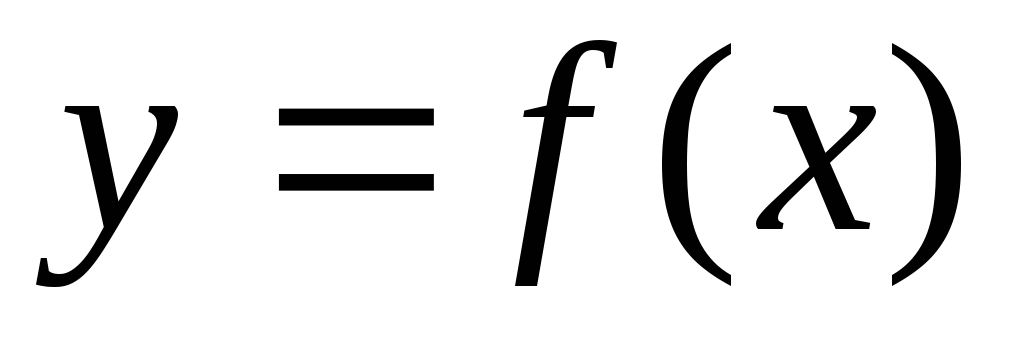
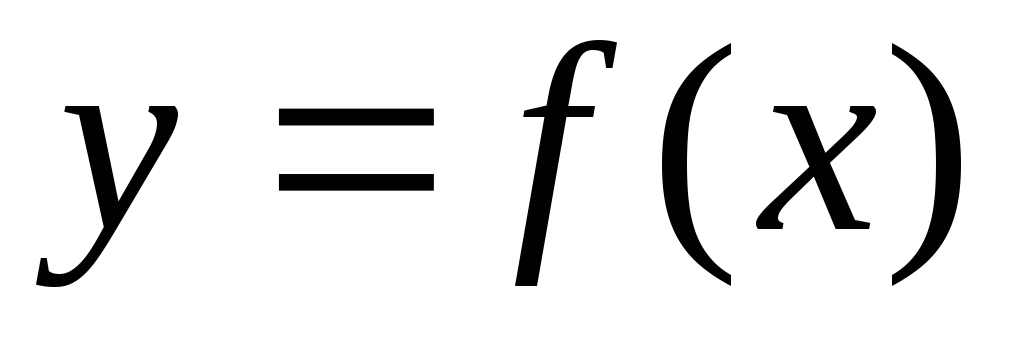
Отличительной чертой любого графика функции 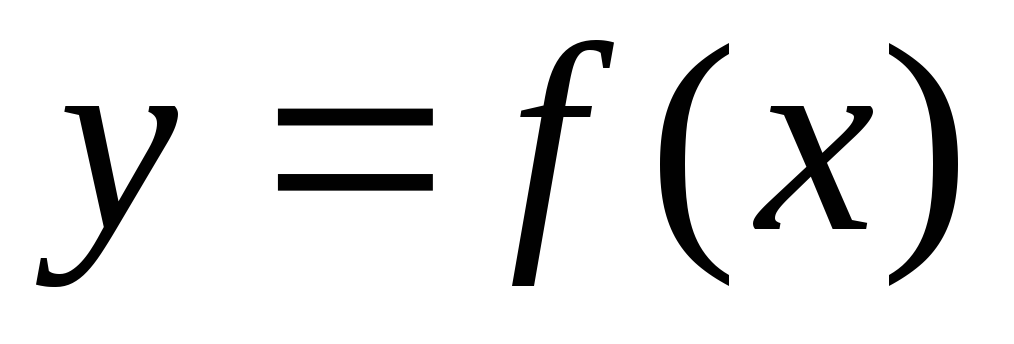



Пример 5. Функция «абсолютная величина 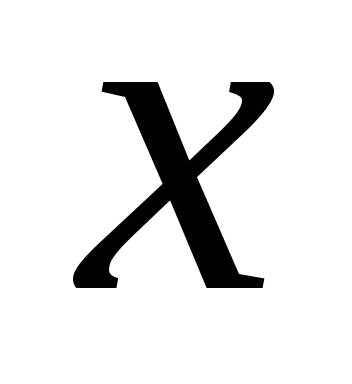
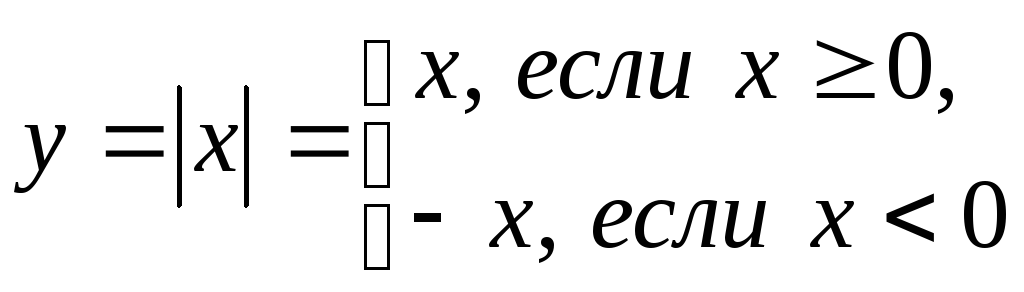
Функция задана с помощью двух функций на разных числовых промежутках. Поэтому график функции «склеен» из двух графиков – графика 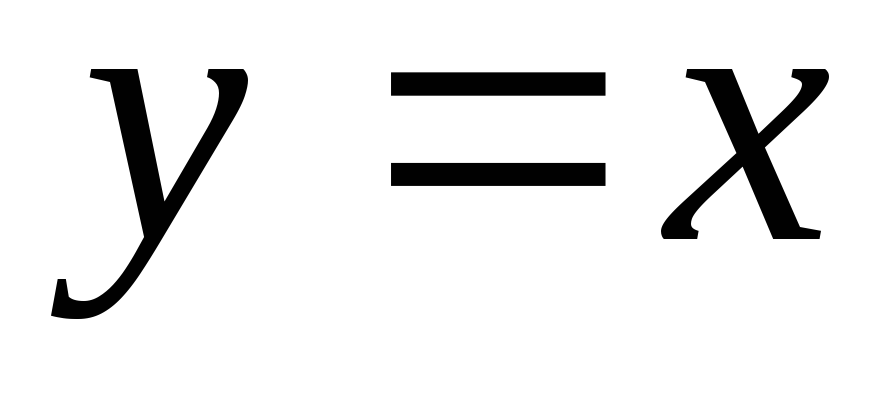
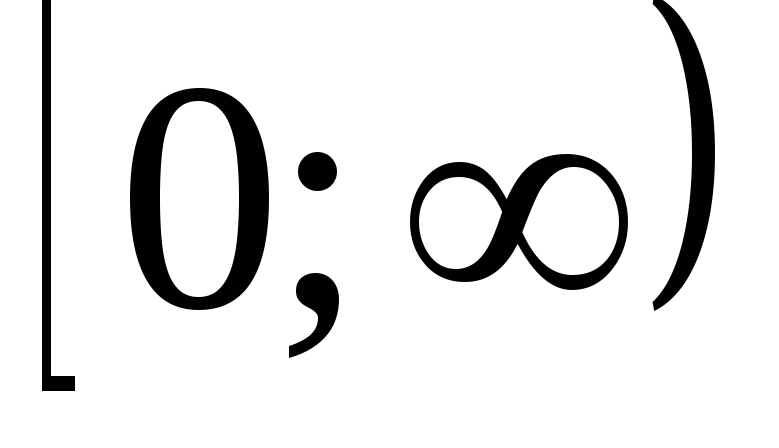

Источник